Appel W. Mathematics for Physics and Physicists

Подождите немного. Документ загружается.

Electromagnetism and the d’Alembertian operator 417

Since the poles are located outside this contour, the integral is equal to

zero:

(ret)

( r, t) ≡ 0 for t < 0.

For posit ive values of t, we have to close the contour in the lower half-plane,

and both poles a re th en inside the contour. Since the path is taken with the

clockwise (negative) orientation, we ﬁnd t hat for t > 0 we have

(ret)

−izt

− z

dz = −2iπ Res



−izt

− z

; z = ±ck



−iπ



ickt

−e

−ickt



and h ence

(ret)

( r, t) =

4π

+∞

sin(kr)

−iπk



ickt

−e

−ickt



8π

+∞



ik(r −c t)

−e

−ik(r −c t)

−e

ik(r +c t)

+ e

−ik(r +c t)



8π

+∞

−∞



ik(r −c t)

−e

ik(r +c t)



4πr



δ(r − c t) −δ(r + c t)



since

ikx

dk = 2π δ(x) (see the table page 612). Because t is now strictly

positive and r ¾ 0, the distribution δ(r + c t) is identically zero on the whole

space. In conclusion, we have obt ained

(ret)

( r, t) =

4πr

δ(r − c t) for t > 0.

Note that this formula is in fact also valid for t < 0, since the remaining

Dirac distribut ion is then id ent ically zero.

Similarly, the advanced Green function is zero for positive times and is

given for all t by

(ad)

( r, t) =

4πr

δ(r + c t) for t < 0,

(ad)

( r, t) ≡ 0 for t > 0.

Physical interpretation

The retarded Green function is represented by a spherical “shell,” emitted at

t = 0 and with increasing radius r = c t. The fact that this pulse is so localized

explains why a light ﬂash (from a camera, for instance) is only seen for a time

418 Gr een functions

equal to the length of time it was emitted

but with a delay proportional to

the distance. Moreover, the amplitude of t he Green function varies like 1/r,

which is expected for a potential.

15.3.b Retarded potentials

Coming back to equation (15.4) for potentials in Lorenz g auge, we obtain using

the retarded Green function for the d’Alembertian that

(ret)

( r, t) =



(ret)

∗



( r, t), A

(ret)

( r, t) =



(ret)

∗µ



( r, t),

(ret)

( r , t) =

4πǫ

ZZZ

Z

+∞

−∞

ρ( r

′

, t

′

)

kr − r

′



kr − r

′

k− c(t − t

′

)



′



′

We can integrate

the time variable t

′

. Since c δ(r − c t) = δ(t − r/c), only

the value t

′

= t −kr − r

′

k/c need be kept, which gives

(ret)

( r, t) =

4πǫ

ZZZ



′

, t −kr − r

′

k/c



kr − r

′

Each “integration element” therefore gives the contribution of the charge ele-

ment situated at the point r

′

at the “retarded time” τ = t −kr − r

′

k/c.

Similarly, we ﬁnd that

(ret)

( r, t) =

4π

ZZZ



′

, t −kr − r

′

k/c



kr − r

′

Remark 15.6 Only a special solution has been described h ere. Obviously, the potential in

space is the sum of this special solution and a free solution, such that A = 0. If boundary

conditions are imposed, the free solution may be quite difﬁcult to ﬁnd. In two dimensions, at

least, techniques of conformal transformation may be helpful.

Lower-dimensional cases

We consider the analogue of the previous problem in one and two dimensions,

starting with the latter. First, it must be made clear what is meant by “two-

dimensional analogue.” H ere, it will be the study of a system described by a

potential ﬁeld satisfying the d’Alembert equation in dimension 2. Note that the

ensuing theory of electromagnetism is extremely different from the theory of

“standard” electromagnetism in dimension 3. Especially notable is that the

Disregarding th e phenomenon of retinal persistence.

Note that clearly we should never write this integral in this manner, since distributions are

involved. We forgo absolute rigor in order to show a computation similar to those which are

exposed, often very quickly, in books of (classical and quantum) ﬁeld theory.

Electromagnetism and the d’Alembertian operator 419

Coulomb potential is not in 1/r but rather logar ithmic,

and the magnetic

ﬁeld is not a vector but a simple scalar.

What about the Green function of the d’Alembertian? It is certainly possi-

ble to argue using a method identical with the preceding one, but it is simpler

to remark that it is possible to pass from the Green function in dimension 3

to the Green function in dimension 2 by integrating over one of the space

variables:

THEOREM 15.7 The Green functions of the d’Alembertian in two and three dimen-

sions are related by the relation

(2)

(x, y, t) =

+∞

−∞

(3)

(x, y, z

′

, t) dz

′

which may be seen as the convolution of G

(3)

with a linear Dirac source:

(2)

(x, y, t) = G

(3)

′

, y

′

, z

′

, t

′

) ∗δ(x

′

− x) δ( y

′

− y) δ(t

′

− t) 1(z

′

Proof. Recall that G

(3)

(x, y, z, t) = δ(x) δ( y) δ(z) δ(t). Passing to the Fourier

transform (and putting c = 1 in the proof), we obtain the relation

−k

) G (k

, z) = 1, (15.7)

which h ol ds for all k

and z. We now put T (x, y, t)

def

+∞

−∞

(3)

(x, y, z

′

, t) dz

′

and

compute 

(2)

T . Passing again to the Fourier transform, we obtai n with T = F [T ]

that

−k

) T (k

, z) = (z

−k

) G

(3)

, 0, z),

which is equal to 1 according to equation (15.7) for k

= 0. Hence we get

−k

) T (k

, z) = 1,



(2)

T (x, y, t) = δ(x) δ( y) δ(t),

which is the equation deﬁning the Green function of the d’Alembertian in two dimen-

sions, and t h erefore G

(2)

= T (up to a free solution).

We have therefore obtained

(ret)

(2)

(x, y, t) =

4π

+∞

−∞

+ z

′2



+ z

′2

− c t



′

where r

def

+ y

Since f ( r) = log kr k does satisfy △f = −2πδ in two dimensions, see equation (7.11)

page 208.

See Chapter 17, page 483, concerning differential forms for an explanation of this seem-

ingly bizarre phenomenon.

420 Green functions

Once more, this function is identically zero for negative values of t. For

positive values of t, we use the rule (explained in Theorem 7.45, page 199)



f (z)



y∈Z



′

( y)



δ(z − y) with Z

def



y ; f ( y) = 0



which is valid if the zeros of f are simple and isolated (i.e., if f

′

( y) does not

vanish at the same time a s f ( y)). Applying this formula gives in particular

+∞

−∞



f (z

′

)



g(z

′

) dz

′

y∈Z

g( y)



′

( y)



In the case considered we have f (z

′

) =

+ z

′2

− c t and

′

) =

′

+ z

′2

Z = {z

, z

} with

−r

= −z

After calculations, we ﬁnd

(ret)

(2)

(x, y, t) =







2π

−(x

+ y

)

if c t > (x

+ y

0 otherwis e.

(15.8)

A cylindrical outgoing wave can be seen which, in contrast to what happens

in three dimensions, is not a pulse. In ﬁgure 15.1, we show the radial function

r 7→ G

(ret)

(2)

(r, t) for two values t

and t

with t

> t

It should be remarked that, if we were living in a ﬂat world,

our visual

perception would have been entirely different. Instead of lighting a given

point (the eye of the subject) for a very short lapse of time, a light ﬂash (for

instance, coming f rom a camera) would light it for an inﬁnite amount of time,

although with an intensity rapidly decreasing

with time (roughly like 1/

as shown by formula (15.8)).

Remark 15.8 A number of electromagnetism books comment (or “prove”) the retarded poten-

tials formula by noting that it is perfectly intuitive, “the effect of a charge propagating at the

speed of light, etc.” Unfortunately, this proof based on intuition is utterly wrong, since it com-

pletely disregards th e phenomenon of nonlocality of the Green function of the d’Alembertian

in dimension 2. It is true th at the Green fu nct ion in three dimensions is of pulse type, but it

is dangerous to found intuition on this fact!

The reader can ch eck (using whichever method she prefers) that the Green

function of the d ’Alembertian in one dimension is given by

(1)

(x, t) =

c/2 if c t > x,

0 if c t < x.

As was envisioned by the pastor and academic Edwin Abbo tt (1839—1926) in his extraordi-

nary novel Flatland [1].

Physiologically at least.

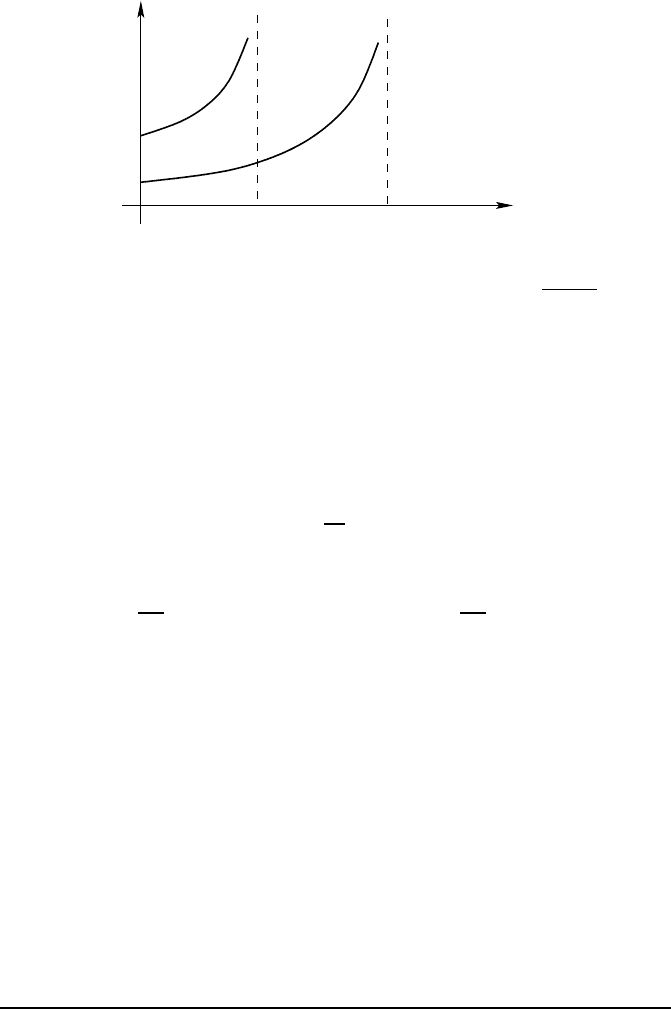
Electromagnetism and the d’Alembertian operator 421

c t

(ret)

(2)

(r, t)

Fig. 15.1 — The ret arded Green function of the d’Alembert ian in two dimensions, for

increasing values t

> t

of the variable t. In the abscissa, r =

+ y

15.3.c C ovariant expression of advance d and retarded

Green functions

The advanced and retarded Green functions may be expressed in a covariant

manner. Denoting x = (c t, x) = (x

, x) and x

= x

− kxk

= x

− r

, we

have (see, for instance, Exercise 8.9, page 242):





= δ(c

− r

) =



δ(r − c t) + δ(r + c t)



which proves that

(ret)

( x, t) =

2π

H (t) δ





and G

(ad)

( x, t) =

2π

H (−t) δ





. (15.9)

Although the function H (t) is not covariant, it should be noticed tha t

H (t) δ





is covariant (it is invariant under Lorentz transformations).

This

is a fundamental property when t rying to write the equations of electromag-

netism or ﬁeld theory in a covariant way [49].

15.3.d Radiation

What is the physical interpretation of the difference G

(ad)

−G

(ret)

We know that the vector potential is given, quite generally, by

A(r) = free solution +

ZZZZ

G(r −r

′

) j(r

′

) d

′

but there are two possible choices (at least) for the Green function, s ince eit her

the retarded or th e advanced one may be used (or any linear combination

In fact, this expression is somewhat ambiguous since, for x = 0, the Dirac distribution

is singular and yet it is multiplied by a discontinuous function. The same ambiguity was,

however, also present in the ﬁrst expression, since it was not speciﬁed what G was at t = 0...

422 Green functions

αG

(ad)

+ (1 − α)G

(ret)

). The incoming a nd outg oing free solutions,

denoted

(in)

and A

(out)

, respectively, are deﬁned by the relations

∀r ∈ R

A(r) = A

(in)

(r) +

ZZZZ

(ret)

(r −r

′

) j(r

′

) d

′

, (15.10)

∀r ∈ R

A(r) = A

(out)

(r) +

ZZZZ

(ad)

(r −r

′

) j(r

′

) d

′

. (15.11)

If the sources j are localized in space a nd t ime, then letting t → −∞ in (15.10),

the integral in the right-hand side vanishes, since the Green function is re-

tarded. The ﬁeld A

(in)

can thus be interpreted as an incoming ﬁeld, coming

from t = −∞ and evolving freely in time. One may also say that it is the

ﬁeld from the past, asymptotically free, which we would like to see evolve since

t = −∞ without perturbing it.

Similarly, the ﬁeld A

(out)

is the ﬁeld which escapes, as ymptotically freely

for t → ∞, that is, it is the ﬁeld wh ich, if left to evolve freely, becomes

(arbitrarily far in the future) equal to the total ﬁeld for t → +∞.

The difference between those two ﬁelds is therefore what is called the ﬁ eld

“radiated” by the current distribution j between t = −∞ and t = +∞. It is

equal to

(ray)

(r) = A

(out)

(r) −A

(in)

(r) =

ZZZZ

G(r −r

′

) j(r −r

′

) d

′

where G(r)

def

= G

(ret)

(r) −G

(ad)

(r).

Hence the ﬁeld A

(ray)

(r) gives, at any point and any time, the total ﬁeld ra-

diated by the distrib ut ion of charges. It is in particular interesting to notice

that, contrary to what is often stated, the unfortunate advanced Green func-

tion G

(ad)

is not entirely lacking in physical sense.

15.4

The heat equation

DEFINITION 15.9 The heat operator in dimension d is the differential oper-

ator

def

= c

∂

∂ t

−µ △

with △

def

∂

∂ x

+ ···+

∂

∂ x

where c > 0 and µ > 0 are positive const ants.

Recall that what is meant by “free” is a solut ion of the homogeneous Maxwell equations

(without source).

The heat equation 423

15.4.a One -dimensional case

The Green function of the problem

We wish to solve the heat equation in one dimension, w hich is the equation



∂

∂ t

−µ

∂

∂ x



T (x, t) = ρ(x, t), (15.12)

where T (x, t) is the temperature depending on x ∈ R and t > 0, and where ρ

is a heat source. The constant c > 0 represents a caloriﬁc capacity and µ > 0

is a thermal diffusion coefﬁcient.

If no limit condition is imposed, th e problem is translation invariant. We

will start by solving the analogue problem when the heat source is elementary

and modeled by a Dirac distribution. This means looking for the solution of

the equation



∂

∂ t

−µ

∂

∂ x



G(x, t) = δ(x, t),

and G will be the Green function of t he heat equation which is also called

the heat kernel.

Taking Fourier transforms, we have the correspondences

G(x, t) 7−→ G (k, ν) =

G(x, t) e

−2iπ(νt+kx)

dt dν,

∂

∂ t

7−→ 2iπν and

∂

∂ x

7−→ −4π

Hence the equation satisﬁ ed by G is



4π

µk

+ 2iπν c



G (k, ν) = 1,

so that

G (k, ν) =

(4π

µk

+ 2iπν c)

There only remains to take the inverse Fourier transforms. We start with the

variable ν. We have

G(k, t) =

2iπνt

(4π

µk

+ 2iπν c)

dν.

A kernel is a function K that can be used to e xpress the solution f of a functional problem,

depending on a function g, in the form

f (x) =

K (x ; x

′

) g(x

′

) dx

′

(for instance, the Poisson, Dirichlet, and Fejér kernels already encountered). The Green func-

tions are therefore also called kernels.

Up to addition of a distribution T satisfying



4π

µk

+ 2iπν c



T (k,ν) = 0.

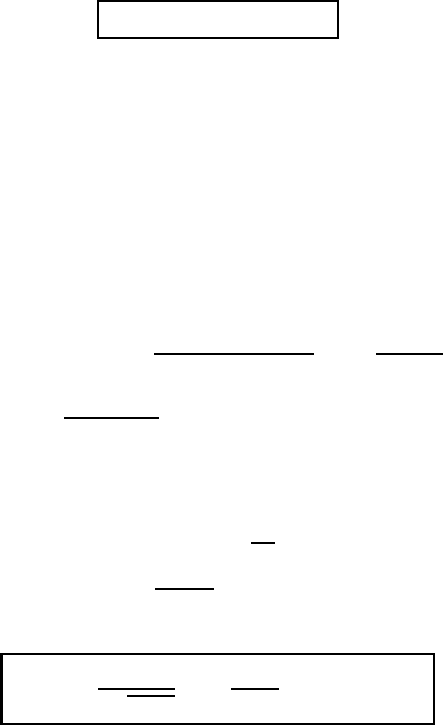
424 Green functions

If ν is considered as a complex variable, the integrand has a unique pole

located at ν

= 2iπµk

/c. Moreover, to evaluate this integral with the method

of residues, we must close the contour of integration of ν in the lower half-

plane if t < 0 and in the upper half-plane if t > 0. The pole being situated in

the upper half-plane, it follows already that

G(x, t) ≡ 0 for t < 0.

This is a rather good thing, since it shows that the heat kernel is causal.

Remark 15.10 It is the presence of unique purely imaginary pole, with strictly posit ive imag-

inary part, whi ch accounts for the fact that there is no “advanced Green function” here. In

other words, this is due to the fact that we have a partial derivative of order 1 with respect to t

and the equation has real coefﬁcients.

In the case of quantum mechanics, the Schrödinger equation is formally i dentical to the

heat equation, but it has complex coefﬁcients. The pole is then real, and both advanced and

retarded Green functions can be introduced.

For positive values of the time variable t, we close the contour in the upper

half-plane, apply Jordan’s second lemma, and thus derive

G(k, t) = 2iπ Res



2iπνt

(4π

µk

+ 2iπν c)

; ν =

2iπµk



−4π

µt/c

(for t > 0).

Remembering that the Fourier transform of a gauss ian is a gaussian, and

that the formula for scaling leads to

−1



−πa



|a|

−πx

(which we apply with a = 2

µπt/c); the inverse Fourier transform in the

space variable is easily performed to obtain

G(x, t) =

µπc t

exp



−c x

4µt



for t > 0. (15.13)

Notice that , whereas temperature is zero everywhere for t < 0, the heat

source, although it is localized at x = 0 and t = 0, leads to strictly positive

temperatures everywhere for all t > 0. In other words, heat has propagated at

inﬁnite speed. (Since this is certa inly not literally the case, the heat equation

is not completely correct. However, given that the phenomena of thermal

diffusion are very slow, it may be considered t hat t he microscopic processes

are indeed inﬁnitely fast, and the heat equaton is per fectly satisfactory for

most thermal phenomena.)

The heat equation 425

Remark 15.11 The “typical distance traveled by heat” is ∆x

= (4µ/c)∆t. This is also what

Einstein had postulated to explain the phenomenon of diffusion. Indeed, a particle under dif-

fusion in a gas or liquid does not travel in a straight line, but rather follows a very roundabout

path, known as Brownian motion, which is characterized in particular by ∆x

∝ ∆t. The

diffusi on equation is in fact formally identical wit h t h e heat equation.

The gaussi an we obtained in (15.13), with variance ∆x

∝ ∆t, can also be interpreted

mathematically as a consequence of a probabilistic result, the central limit theorem, discussed

in Chapter 21.

The problem with an arbitraty heat source (15.12) is now easily solved, since

by linearity we can write

T (x, t) = [G ∗ρ](x, t) =

∞

−∞

+∞

G(x

′

, t

′

) ρ(x − x

′

, t − t

′

) dt

′

. (15. 14)

Note, however, that this general solution ag ain satisﬁes T (x, 0) = 0 for a ll

x ∈ R. We must still add to it a solution satisfying the initial conditions at

t = 0 and the free equation of heat propagation.

Initial conditions

We now want to take into account the initial conditions in the problem of

heat propagation. For this, we impose that the temperature at time t = 0 be

given by T (x, 0) = T

(x) for all x ∈ R, where T

is an a rbitrary function.

We need a solution to the free problem (i.e., without h eat source), which

means such that

T (x, t) = H (t) u(x, t).

The discontinuity of th e solution at t = 0 provides a way to incorporate the

initial condition T (x, 0) = T

(x). Indeed, in the sense of distributions we

have

∂T

∂ t



∂ u

∂ t



+ T

(x) δ(t).

The distribution T (x, t) then satisﬁes the equation



∂

∂ t

+ µ

∂

∂ x



T (x, t) = c T

(x) δ(t),

the solution of which is given by

T (x, t) = c T

(x) δ(t) ∗G(x, t) = c

+∞

−∞

G(x − x

′

, t) T

′

) dx

′

Hence the solution of the problem that incorporates both initial condition

and h eat source is given by

T (x, t) = T (x, t) + T (x, t) =

ρ(x, t) + c T

(x) δ(t)

∗G(x, t).

However, it is easier to take the initial conditions into account when us ing

the Laplace transform, as in the next example.

426 Green functions

15.4.b Three-dimensional case

We are now interested in the three-dimensional case, which we will treat using

the formalism of the Laplace transform.

So we consider a f unction (or, if need be, a distribution) that satisﬁes the

free heat equation with a given boundary condition:

∂ T

∂ t

−µ △ T = 0 and T ( r, 0) = T

( r).

We perform a Laplace transform with respect to the time variable, denoted

T ( r, t) ⊐ T ( r, p). We th en have

(c p −µ△) T ( r, p) = T

( r).

Notice that, t his time, the initial conditions T

( r) are automatically involved

in t he Laplace transform, since the value of the temperature at t = 0 appears

in the differentiation th eorem.

Taking the Fourier transform of this equation, we obtain

T ( k, p) = c

(k) ·

G ( k, p),

were we have denoted

G ( k, p) =

c p + 4π

µ k

p + 4π

µ k

. (15.15)

A formal solution is then ob tained by ta king successively the inverse Laplace

transform:

T ( k, t) = c

(k) ·

G( k, t),

and then the inverse Fourier transform:

T ( r, t) = c



∗G



( r, t) =

ZZZ

c T

( r

′

) G( r − r

′

, t) d

′

In order to obtain the function G( r, t), we come back to the expression (15.15)

and use the table of Laplace transforms on page 614:

G( k, t) =

H (t)

−4π

µ k

t/c

whence (the inverse Fourier transform of a gaussian in three dimensions)

G( r, t) =

8(πµt)

3/2

−c r

/4µt

. (15.16)

The reader should not, however, get the impression that this is vastly p referable in three

dimensions: we could just as well use the method of the one-dimensional case, or we could

have treated the latter with the Laplace transform.