Appel W. Mathematics for Physics and Physicists

Подождите немного. Документ загружается.

Quantum mechanics 427

Remark 15.12 We may add a right-hand side to the heat equation: D T ( r, t) = ρ( r, t), where

ρ is the distribution describing the heat source; it allows us to derive a more general solution

(where the convolution is both on time and space variables)

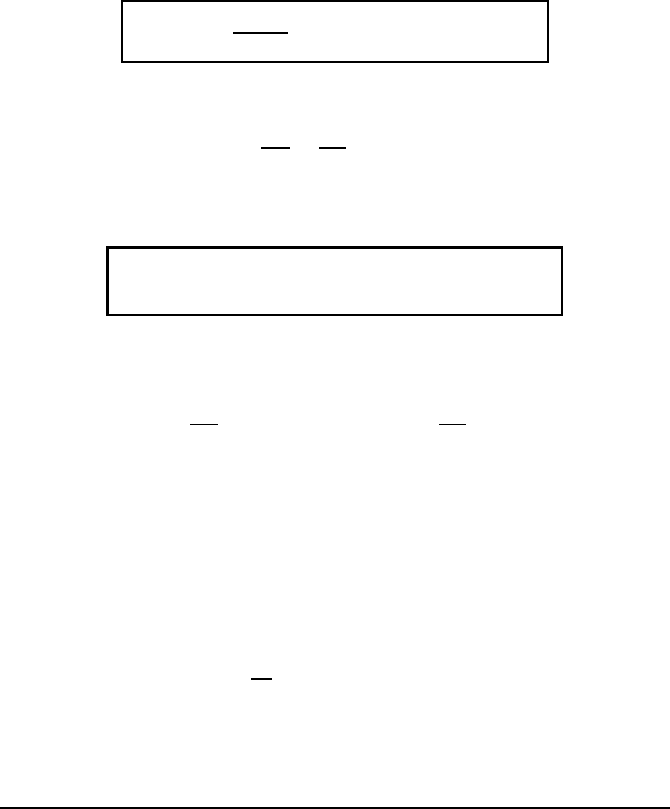
T ( r , t) =



ρ + c T

( r) δ(t)



∗G

( r, t).

Remark 15.13 Here also the typical distance of heat propagation is ∆x

∝ ∆t. This result

(still a consequence of the central limit theorem!) is independent of the dimension of the

system.

15.5

Quantum mechanics

This time, we consider the evolution equation for a wave function:

DEFINITION 15.14 The Schrödinger operator is the differential operator

i }h

∂

∂ t

△ − V ( r),

where m is the mass of the particle and V ( r) is a potential independent of

time. If V ≡ 0, this is the free evolution equation.

In fact, only the free ca se V ( r) ≡ 0 will be treated here. Notice that this

operator is formally similar to the heat operator with µ = i }h/2mc. How-

ever, its propert ies are very different, since in particular the heat equation

is irreversible, whereas the Schrödinger equation is perfectly reversible. This

is due to the fact that the Schrödinger equation is applied to complex-valued

functions.

The Green function of the Schrödinger operator is computed in exactly

the same manner as in Section 15.4

and leads to

G ( p, t) = e

−i p

}ht/2m

= e

−iH t/ }h

for t > 0,

In the Schrödinger equation, it is therefore possible to perform the transformation t 7→ −t

and simultaneously to map ψ 7→ ψ, so that the equation is still satisﬁed. Note t h at ψ and ψ have

the same physical interp retation (since the square o f the modulus is the probability density of

the particle). Finally, notice that the change of ψ into ψ simply amounts to a change of

convention and to changing i into −i, which cannot affect physics. The operator i }h∂/∂ t is

indeed invariant when simultaneously t 7→ −t and i 7→ −i.

This calculation involves a slight additional difﬁculty in that one must extract t h e square

root of a quantity which is this time imaginary. Hence a determination of the functi on

z 7→

z must be speciﬁed, involving a cut in the plane. Once this is done, there is no fur ther

difference. In the text, we have chosen a cut along the positive imaginary axis.

428 Green functions

(where we write H = p

/2m in momentum representation), taking p as

the conjugate variable to x and using th e standard convention in quantum

mechanics:

G ( p, t) =

ZZZ

G( x, t) e

i p·x/ }h

Similarly, with the inverse Fourier transform, we obtain the equivalent

of (15. 16):

G( r, t) =



2iπ }ht



3/2

im|r|

/2 }ht

for t > 0. (15.17)

If we want to solve the free Schrödinger equation

i }h

∂ψ

∂ t

△ψ = 0

with initial conditions ψ( r, 0) = ψ

( r), we get

the relation for the propaga-

tion of the wave function:

ψ( r, t) =

G( r − r

′

, t) ψ

( r

′

) d

′

for t > 0. (15.18)

The function G is called the Schrödinger kernel. Equation (15.18) is therefore

perfectly equivalent to the Schrödinger equation written in the form

i }h

∂ψ

∂ t

= H ψ with H

def

= −

△. (15.19)

Either form may be used as a postulate for the purpose of the formalization

of quantum mechanics.

It should be noted that th e general form of the Green function (15.17)

may be obtained through the very r ich physical tool of path integrat ion. The

reader is invited to look at the book of Feynman and Hibb s [34] to learn

more about this .

Note also that, using Dirac’s notation, we can write the evolution equation

of the particle as

i }h



ψ(t)



= H



ψ(t)



(denoting by |ψ〉 the wave vector of the particle), which can be solved —

formally — by putting



ψ(t)



= e

−iH t/ }h

|ψ

〉.

Once more, those initial conditions are taken into accound by adding a right-hand side

given by ψ

( r ) δ(t).

Klein-Gordon equation 429

Using the “closure relation” 1 =

′

〉〈r

′

(see Theorem 14.26) we obtain

for all t that

ψ( r, t) =





ψ(t)







−iH t/ }h



′



′





′





−iH t/ }h



′



( r

′

) d

′

This is recognizable as the s ame integral as in (15.18). Since this relation

should be kept only for positive time, we are led to write

G( r − r

′

, t) = H (t)





−iH t/ }h



′



In terms of Fourier transforms, we do indeed get

G ( p, t) =





−iH t/ }h





= e

−i p

}ht/2m

which shows that the two expressions are consistent (and illustrates the sim-

plicity of the Dirac nota tion).

15.6

Klein-G ordon e quation

In this section, the space and time variables will be expressed in a covariant

manner, that is , we will put x = (c t, x) = (x

, x) and p = (p

, p). We choose

a Minkowski metric with signature (+, −, −, −), which means that we put

= p

− p

, x

= x

− x

, and  =

∂

∂ t

−△.

Remark 15.15 Note that the sign of the d’Alembertian is oppo site to that used in

Section 15.3; here we conform w ith relativistic customs, w h ere usually  = ∂

∂

with

a metric ( +, −, −, −).

We want to solve an equation of the type

( + m

) ϕ(x) = j(x),

which is called the Klein-Gordon equation for the ﬁeld ϕ (it originates in

ﬁeld theory). In this equation, m represents the mass of a particle, j is an

arbitrary source and ϕ is the ﬁeld which is the unknown. As usual, we take

the constants }h and c to be equal to 1.

Otherwise we should write ( }h

 + m

) ϕ = j.

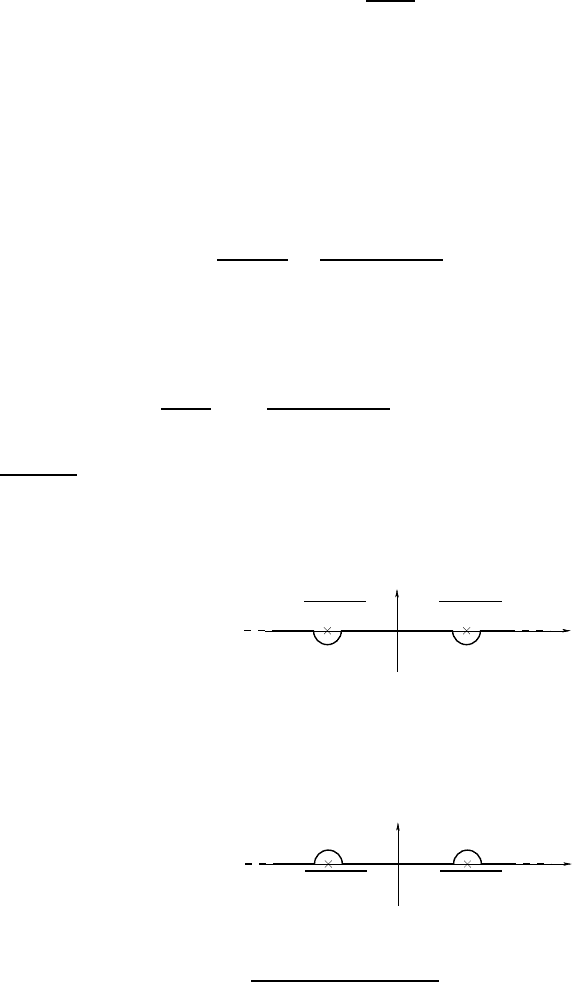
430 Gr een functions

To harmonize notation with thos e which are customary in ﬁeld theory,

the Fourier transform and its inverse are denoted as follows:

f (p) =

f (x) e

ip·x

x and f (x) =

(2π)

f (p) e

−ip·x

We start by trying to solve the equation where the source term is replaced by

a D irac distribution; the Green function of this equation

( + m

) G(x) = δ

(x)

is called a propagator. Taking the Fourier transform, we get

(−p

+ m

) G (p) = 1,

or G (p) =

−1

−m

−1

− p

−m

As in the case of electromagnetism, there will arise a problem with this de-

nominator when performing the inverse Fourier transform. Indeed, we will

try to write an expression like

G(x) = −

(2π)

ZZZZ

− p

−m

−ip·x

p dp

During the process of integ rat ing over the variable p

, two poles at p

+ m

occur. They must be bypassed by seeing p

as a variable in the

complex plane and integ rat ing along a deformed contour (see Section 15.2).

For instance, we may go around b oth poles in small half-circles in the

lower half-plane, which provides the advanced Green function:

(ad)

(t, x)

given by the path

−−−−−−−−→

−

+ m

∈ C

This also amounts to adding a negative imaginary part to p

, if integrating

ﬁrst over p is preferred.

Similarly, the retarded Green function is deﬁ ned by going around both

poles in the upper half-plane, or equivalently, by adding a small positive imag-

inary part to p

(ret)

(t, x)

given by the path

−−−−−−−−→

−

+ m

∈ C

Hence we put

(ad)

(p)

def

−1

−iǫ)

− p

−m

Klein-Gordon equation 431

and

(ret)

(p)

def

−1

+ iǫ)

− p

−m

Taking inverse Fourier transforms, we obtain

(ad)/(ret)

(x) = −

(2π)

ZZZZ

−ip·x

∓iǫ)

− p

−m

By the residue theorem, the function G

(ret)

is zero for t < 0 and G

(ad)

zero for t > 0. Moreover, these Green functions being deﬁned by Lorentz

invariant objects, it follows that G

(ret)

is zero outside the f ut ure light cone (it

is said to be causal in the relativistic sense) and G

(ret)

outside of th e past light

cone. Also, note that b oth functions are real-valued (despite the presence of

the term iǫ) and that G

(ret)

(−x) = G

(ad)

(x).

Whereas, in t he case m

= 0 of electromagnetism,

we had a simple ex-

plicit formula for the Green functions, we would here get Bessel functions

after integrating on the variable p. The full calculation is not particularly

enlightening, and we leave it aside. Note, h owever, that the Green functions

are no longer supported on the light cone as with (15.9) (the case m

= 0);

there is also propagation of signals at speeds less than the speed of light. This

is of course consistent with having a nonzero mass!

To close this very brief section (referr ing the reader to [49] for a wider

survey of the properties of the Green fnctions of the Klein-Gordon equation),

we mention that it is possible to introduce a very different Green function,

following Stueckelberg and Feynman. Let

(p) =

−1

−m

+ iǫ

From the formula

−α

+ iǫ ≈



x + α −

iǫ

2α



x −α +

iǫ

2α



which is valid to ﬁrst order in ǫ, we deduce that changing m

into m

− iǫ

amounts to changing the poles

(1)

= −

+ m

and p

(2)

+ m

into, respectively,

−

+ m

+ iǫ

′

and

+ m

−iǫ

′

with ǫ

′

= ǫ/2

+ m

, or to take the following integration contour:

Which is indeed a zero-mass ﬁeld theory.

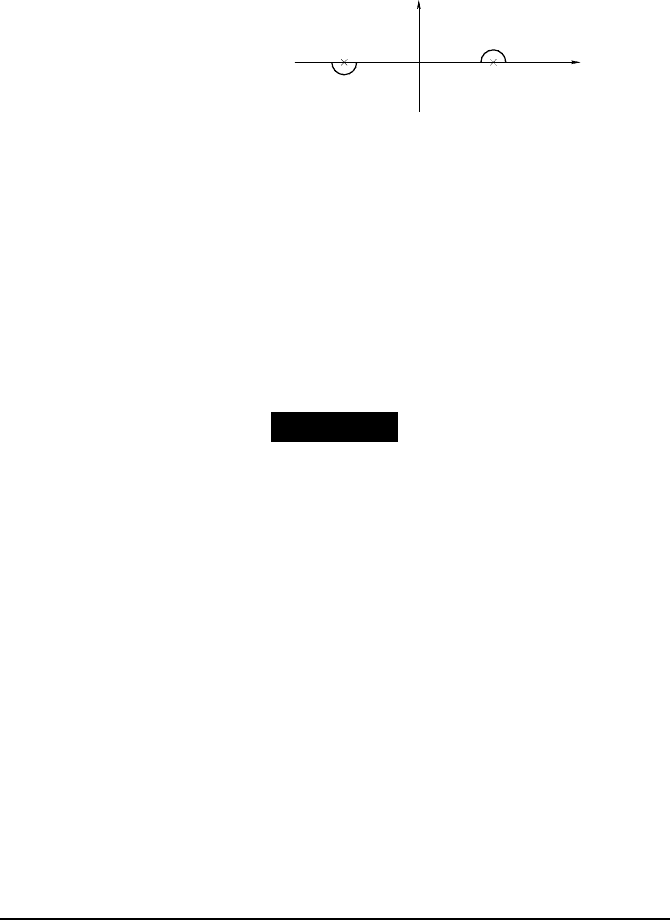
432 Green functions

(t, x)

given by the path

−−−−−−−−→

This last Green function is called th e Feynman propagator

; it is complex-

valued and does satisfy (− + m

) G

(x) = δ(x), as well as the relation

(x) = G

(−x). Moreover, it can be shown (see [49]) that this propagator

is not zero outside the light cone (i.e., in particular that G

(0, r ) is not

identically zero for values of r 6= 0, contrary to wha t happens with th e

“advanced” and “retarded” functions).

Remark 15.16 Why does this function not appear in “classical” physics? Simply because only

(ad)

and G

(ret)

are real-valued and have a p hysi cal meaning that is easy to grasp. The Feyn-

man propagator G

is complex-valued; however, it makes sense in quantum mechanics, where

functions are intrinsically co mplex-valued.

EXERCISES

 Exercise 15.1 Show that the Green function of the d’Alembertian is of pulse type in odd

dimensions at least equal to 3, but that otherwise it is not localized.

 Exercise 15.2 (Damped harmonic oscillator) A damped harmonic osc illator is ruled by the

following ordinary differential equation:

′′

+ 2a y

′

+ ω

y = f ,

where a is some positive parameter. We are looking for the Green function associated to the

equation y

′′

+ 2a y

′

+ ω

y = δ.

i) What i s the equation which is satisﬁed by the Fourier transform of the Green function

ii) Compute the Green function in D

′

. One may represent graphically th e poles of the

meromorphic function that appears during the calculations.

iii) Find the solution of the equation with an excitati on f (some assumptions on f may

be required).

Richard Phil l ips Feynman (1918—1988), American physic ist, was one of the inventors of

quantum electrodynamics (the quantum relativistic theory of electromagnetism), which is con-

sidered by many as “o ne of t h e most beautiful current physical theories.” Wit h a penetrating

mind and a physical sense particularly acute and clear, he simpliﬁed the perturbative methods

and invented the diagrams that were named after him, which are extremely useful both for

making computations and for understanding t h em. His physics lecture notes are indispensable

reading and his autobiography is funny and illuminating in many respects.

Chapter

Tensors

In this chapter, we will give few details concerning the practical handling of tensors,

or the usual calculation tricks, juggling wi th indices, contractions, recognition of

tensors, etc. Many excellent books [5,27,35,57,62,92] discuss those rules (and often

do much more than that!)

Here, the focus will be on the mathematical construction of tensors, in order to

complement the “computational” vi ewpoint of th e physic ist. This chapter is there-

fore not directed to physicists tryi ng to learn how to tensor, but rather to those

who, having started to manipulate tensors, would like to understand what is hidden

behind.

Also, since this is a purely introductory chapter, we only discuss tensors in a ﬂat

space. There wi l l be no mention of parallel transport, ﬁber bundles, c o nnections,

or Christoffel symbols. Readers wi shing to learn more should consult any of the

classical textbooks of differential geometry (see Bibliography, page 617).

16.1

Tensors in afﬁne space

Let K denote either th e real ﬁeld R or the complex ﬁeld C. We identify

E = K

, a vector s pace of dimension n, with an afﬁne space E of the same

dimension, We consider E with a basis B

def

= (e

)

= (e

, . . . , e

16.1.a Vectors

Let u be a vector in E , that is, an element of K

. There exists a unique

expression of u as linear combination of the basis vectors of B:

434 Tensor s

DEFINITION 16.1 (Contravariant coordinates of a vector) The contravariant

coordinates of a vector u are the unique elements (u

)

in K such that

u =

µ=1

= u

+ ···+ u

The contravariant coordinates are th erefore the “usual coordinates” of linear

algebra.

Remark 16.2 Obviously, for a given vector u, the µ-th coordinate depends not only on the

vector e

, but also on all other vectors of the chosen basis.

Remark 16.3 From the poi nt of view of a physicist, what quantities may be modeled by a

vector? If working in R

, a vector is not simply “a triplet of real numbers”; rather, it possesses

an additional property, related to changes of reference frame: if an observer performs a rotation,

the basis vectors turn also, and all triplets that are called “vectors” are transformed in a uniform

manner. A triplet “(temperature, pressure, density),” for instance, does not transform in the

same way, since each component is invariant under rotations (they are scalars).

In what manner a re the coordinates of a vector transformed during a

change of basis? Let B

′

= (e

′

)

denote another basis of E . We write L the

matrix for the cha nge of basis from B to B

′

, that is, t he matrix where the µ- th

column represents the vector e

′

, as expressed in coordinates in the basis B

(see Appendix C). Writing this matrix L = (L

)

νµ

, where ν is the line index

and µ the column index , it follows that for all µ ∈ [[1, n]] we have

′

ν=1

. (16.1)

The left index in L

is the row index, and the right index is the column index.

For reasons which will become clearer later on, the ﬁrst index is indicated in

superscript and the second in sub script. Symbolically, we write

′

= L B.

Let Λ

def

= L

−1

be the inverse matrix L, i.e., the unique matrix wit h coefﬁ-

cients (Λ

)

µν

that satisﬁes

ν=1

= δ

for all µ, ν ∈ [[1, n]]. The vectors of B can be expressed as functions of th ose

of B

′

by means of the matrix Λ:

Note that this is not a matrix relation. However, one can formally build a line vector with

the e

’s and write

′

, . . . , e

′

) = (e

, . . . , e

) · L.

Tensors in afﬁne spac e 435

B = Λ B

′

or e

ν=1

′

By writing the decomposition of a vector in the two bases, we can ﬁnd the

transformation law for the coordinates of a vector:

u =

′µ

′

µ,ν

(Λ

′

) =

µ,ν

′µ

), (use (16.1))

µ,ν

(Λ

′

) =

µ,ν

′ν

), (change names)

hence, by uniqueness of the decomposition in the basis B and B

′

, respectively,

we have

′µ

ν=1

and u

ν=1

′ν

. (16.2)

Remark 16.4 These last formulas are also a criterion for being a vector: an n-uple, the com-

ponents of which are transformed according to (16.2) during a change of basis (for example,

when an observer performs a rotation) will be a vector. In w h at follows, saying that “we want

to prove that a certain quantity is a vector” will simply mean that we w ish to establish the

relations (16.2).

16.1.b Einstein convention

Very quickly, the formulas for changes of coordinates become unreadable be-

cause of the increasing accumulation of indices of summation signs. This is

why Einstein

suggested omitting the summation sign, which is implied each

time a Greek letter appears one time, and one time only, as a subscript and one time,

and one time only, as a superscript. Thus, relations (16.1) and (16.2) are expressed

as follows using the Einstein convention:

′

= L

and e

= Λ

′

, (16.1

′

)

′µ

= Λ

and u

= L

′ν

. (16.2

′

)

Remark 16.5 One should be aware also that many books of relativity theory use the same lett er Λ

to denote both matrices Λ and L. Two solutions are used to avoid conﬂicts:

• In the book of S. Weinberg [92], for instance, they are distinguished by the position of

indices. Thus, Λ

represents what we denoted L

, whereas Λ

is the same as ours.

Albert Einstein (1879—1955), German — then Swiss, then American when, being Jewish, he

ﬂed Nazi Germany — physicist and mathematician, student of Hermann Minkowski, father of

special relativity (1905) then general relativity (around 1915), used and popularized the tensor

calculus, in particular by th e introduction of riemannian geometry in physics.

436 Tensor s

• In the book of Ch. Misner, K. Thorne, and J. A. W h eeler [67], for instance, a primed

superscript indicates that Λ is being understood, and a primed subscript th at L is

understood.

Each notation has its advantages; the one we chose i s closer to “classical” linear algebra. Here

is a short summary of various conventions in use, where • is used to indicate any tensor object:

this book L

•

= L

•

′

•

′µ

= Λ

•

Weinberg Λ

•

= Λ

•

′

•

′µ

= Λ

•

Wheeler Λ

′

•

= Λ

′

•

′

•

′µ

= Λ

′

•

16.1.c Lin ear forms

We recall the following deﬁnitions:

DEFINITION 16.6 A linear form on E in any linear map from E to K.

DEFINITION 16.7 The dual of E , denoted E

∗

, is the vector space of linear

forms on E . For ωω

ωω ∈ E

∗

, we denote either ωω

ωω(v) or 〈ωω

ωω, v〉 the effect of

evaluating the linear form ωω

ωω on a vector v ∈ E . Similarly, we sometimes write

〈ωω

ωω, ·〉 instead of ωω

ωω.

Example 16.8 The coordinate linear forms

: R

−→ R,

, . . . , h

) 7−→ h

deﬁned for i = 1, . . . ,n, are linear forms.

For a ﬁxed vector u ∈ E , the map

ψ : E

∗

−→ K,

ωω

ωω 7−→ 〈ωω

ωω, u〉

is K-linear, hence it is an element in E

∗∗

. This application can only be

identically zero if u = 0. This shows that by as sociating it to u, we deﬁne an

injective map from E into E

∗∗

. In general, this is not a surjection. However,

it is so in two important cases: in Hilbert spaces (when considering only

continuous linear forms and linear forms deﬁned by scalar products), and

when E is a ﬁnite-dimensional vector space:

THEOREM 16.9 (Bidual) Let E be a ﬁnite-dimensional K-vector space. Then we

have E ≃ E

∗

, dim E

∗

= dim E , and moreover E and E

∗∗

are canonically isomor-

phic.

THEOREM 16.10 (Dual basis) L et (e

)

be a basis of E . The family (αα

αα

)

elements of E

∗

is deﬁned by its action on any basis vector (e

)

given by

∀µ, ν ∈ [[1, n]] 〈αα

αα

, e

〉 = δ

1 if µ = ν,

0 if µ 6= ν.