Appel W. Mathematics for Physics and Physicists

Подождите немного. Документ загружается.

Chapter

Green func tions

This chapter, properly speaking, is not a course on Green functi o ns, and it does not

really introduce any new object or concept. Rather, through some simple physical

examples, it explains how the various techniques discussed previously (Fourier and

Laplace transforms, conformal maps, convolution, differentiation in the sense of

distributions) can be used to solve easily certain physical problems related to linear

differential equations.

The ﬁrst problem concerns the propagation of electromagnetic waves in the vac-

uum. There the Green function of the d’Alembertian is recovered from scratch, as

well as the retarded potentials formula for an arbitrary source distribution.

The second problem is the resolution of th e h eat equation, using either the Fourier

transform, or the Laplace transform.

Finally, it will be seen how Green functions occur naturally in quantum mechan-

ics.

15.1

Generalities about Green functions

Consider a linear system with input signal I and output (or response)

signal R. This is described by an equation of the type

Φ(R) = I.

What we called “input signal” and “output signal” could be many things, such

as:

• electrical signals in a circuit (for instance, power as input and response

of a component as output);

408 Green functions

• charges and currents a s input and electromagnetic ﬁelds as output;

• heat sources as input and temperature as output;

• forces as input and position or velocity as output.

The operator Φ is linear and continuous. It may depend on variables such

as time or position. I n this chapter, we are interested in the case where it is

translation (spacial or temporal) invariant.

Most of the time, Φ is a differential

operator (such as a Laplacian, d’Alembertian, etc.).

Since Φ is at the s ame time continuous, linear, and translation invariant,

it is known that it may be expressed as a convolution operator; hence there

exists

a d istribution D such that I = Φ(R) = D ∗R. The Green function of

the system is deﬁned to be any distribution G satisfying the equation

Φ(G) = D ∗G = G ∗ D = δ,

where the Dirac distribution δ “applies” to t he spacial or temporal variable

or variables of the system. Computing the convolution product of the input

signal with the Green function, we get

G ∗ I = G ∗(D ∗ R) = (G ∗ D) ∗ R = δ ∗R = R,

which shows that knowing the Green function is sufﬁcient in principle to

compute R from the knowledge of the input I. However, complications arise

when different Green functions exist in different algebras (for insta nce, in

electromagnetism, two distinct Green functions lead, respectively, to retarded

and advanced potentials).

Thus, th is chapter’s goal is to provide some examples of explicit compu-

tation techniques available to compute the Green functions, using mainly the

Fourier and Laplace transforms. The strategy used is always the same:

i) take the Fourier or Laplace transform of the equation;

ii) solve the resulting equation, w hich is now algebraic;

iii) take the inverse transform.

This may also be symbolized as follows:

D ∗G = δ =⇒







D ·

G = 1

D ·

G = 1

=⇒







G = 1/

=⇒







G = F [1/

G ⊐ 1/

Despite the simplicity of this outline, difﬁculties sometimes obstr uct the way;

we will see how to solve th em.

Still, an example which is not translation invariant is treated in Section 6.2.a on page 165.

It sufﬁces to put D = Φ(δ).

A pedagogical example: the harmonic oscillator 409

15.2

A pedagogical example: the harmonic oscillator

We treat here in detail a simple example, which contains the essential dif-

ﬁculties concerning the computa tion of Green functions, without extraneous

complications (temporal and spacial variables together).

A Green function of the harmonic oscillator is a function t 7→ G(t) that

is a solution, in the sense of distributions, of t he equation

′′

(t) + ω

G(t) = δ(t), (15.1)

where ω

> 0 is a ﬁxed real number. This amounts to saying th at G is a

convolution inverse of the operator (δ

′′

+ ω

δ), and we have already s een

expressions for this in Theorem 8.33 on page 239.

We discuss here two methods that lead to the discovery of such a Green

function of the harmonic oscillator (in addition to the “manual” method of

variation of the constant,

which does not generalize very well).

We quickly recall how the differential equation

′′

+ y = f (t) (E)

can be solved, where f (the exterior excitation) is a continuous function, and wh ere we put

= 1. This is done in two steps:

• Resolution of the homogeneous equation. We know that the space of solutions of the

associated homogeneous equation (namely y

′′

+ y = 0) is a two-dimensional vector space, a

basis of which is, for instance, (u, v) = (cos, sin).

• Search for a particular solution. We use the method of variation of the constants,

generalized for order 2 equations, as follows: look for a solut ion of the type y

= λu + µv,

where λ and µ are functions to be determined. Denoting by W

u,v

the Wronskian matrix

associated to the basis (u, v), which is deﬁned by

u,v



u v

′



those functions are given by



′



= W

−1

u,v







cos t sin t

−sin t c o s t



−1



f (t)



that is,

′

= −sin(t) f (t) and µ

′

= cos(t) f (t),

so t hat (up to a constant, which can be absorbed in the solution of the homogeneous equation)

we have

λ(t) = −

sin(s) f (s) ds and µ(t) =

cos(s) f (s) ds.

Using the trigonometric formula sin(t − s) = sin t cos s − cos t sin s, we deduce

(t) =

f (s) sin(t − s) ds.

410 Gr een functions

15.2.a Usin g the Laplace transform

Denote by G (p) the Laplace transform of G(t). In the Laplace world, equa-

tion (15.1 ) becomes

+ ω

) ·G (p) = 1.

Since G is a function, and not a distribution, we therefore have

G (p) =

+ ω

and hence, using for instance a table of Laplace transforms (see page 613), we

have

G(t) =

H (t) sin(ω

t).

Remark 15.1 On the one hand, this is quite nice, since the computation was very quick. On

the other hand, it may be a li ttle disappoi nting: we found a single ex pression for a Green

function. More precisely, we found the unique inverse image of δ

′′

+ δ in D

′

, and not the

one in D

′

−

(see Theorem 8.33 on page 239). This is quite normal: by deﬁnition of the u nilateral

Laplace transform, only causal input functions are considered (hence they are in D

15.2.b Us ing the Fourier transform

Denote by

G(ν) the Fourier transform of G(t). Equation (15.1) becomes

(−4π

+ ω

)

G(ν) = 1 (15 .2)

in the Fourier world. A ﬁrst trial for a solution, rather naive, leads to

G(ν) =

−4π

. (naive solution)

Then we should take the inverse Fourier transform of

G(ν).

But here a serious difﬁculty arises: the function

G as deﬁned above has

two real poles at ν = ±ω

/2π, and hence is not integrable (nor is it square

integrable). So the inverse Fourier transform is not deﬁned.

In fact, the reasoning was much too fast. The solutions of equation (15.2)

in the sense of distributions are those distributions of the form

G(ν) = pv

−4π

+ α δ



ν −

2π



+ β δ



ν +

2π



, (15.3)

Thus, the general solution of the equation are given by

y(t) =

f (s) sin(t − s) ds + α cos t + β sin t

| {z }

free part

We recognize, for t > 0, the convolution of the function G : t 7→ H (t) sin t and the truncated

excitation function H (t) f (t). The function G is the causal Green function associated to the

equation of th e harmonic oscillator (see Theorem 8.33 on page 239).

A pedagogical example: the harmonic oscillator 411

according to Theorem 8.11 on page 230, wh ere we denote

−4π

2ω



2πν + ω

−pv

2πν −ω



The last two terms of equation (15.3) are the Fourier transforms of the func-

tions t 7→ α e

iω

and t 7→ β e

−iω

, in which we recognize free solutions

(those that sat isfy y

′′

+ y = 0). We could leave them aside, but it is more

useful to ﬁnd interesting valus of α and β.

Indeed, if we take α = β = 0, t his amounts to use a s integration contour

in the inverse Fourier transform the following truncated real line (where ν

/2π):

−ν

2ǫ

in the limit ǫ → 0.

As seen in Section 8.1.c on page 225, we may add to ν

a positive or

negative imaginary part ±iǫ, which amounts to closing the contour by small

half-circles either above or under the poles. Replacing each occurence of ν

+ iǫ, or in other words, putting

G(ν) =

4π ω



ν + ν

+ iǫ

−

ν −ν

−iǫ



leads to a complex-valued function G, which is a priori uninteresting. We will

rather deﬁne

(ret)

(ν)

def

= lim

ǫ→0

4π ω



ν + ν

−iǫ

−

ν −ν

−iǫ



or, equivalently, put β = −α = 1/4ω

(ret)

(ν) =

4π ω



ν + ν

+ iπ δ(ν + ν

) −pv

ν −ν

−iπ δ(ν −ν

)



In the inverse Fourier transform formula

(ret)

(t) =

(ret)

(ν) e

2iπνt

dν,

this corresponds to the integration contour γ sketched below:

(ret)

(t)

given by the path

−−−−−−−−→

−ν

412 Green functions

Since the inverse Fourier transform of

2iπ





is H (t), it follows th at

2iπ



ν + ν



δ(ν + ν

)

T.F.

−1

−−−−→ H (t) e

−iω

and

2iπ



ν −ν



δ(ν −ν

)

T.F.

−1

−−−−→ H (t) e

iω

Hence the inverse Fourier transform of

(ret)

(t) =

2ω

H (t)



i e

−iω

−ie

iω



H (t) sin(ω

t).

Remark 15.2 It is no more difﬁcult, if the formula is forgotten and no table of Fourier

transforms is handy, to perform the integration along the contour indicated using the residue

theorem. The sign of t must then be watched carefully, since it dictates whether one should

close the integration contour from above or from below in the complex plane.

In the case discussed here, for t < 0, the imaginary part of ν must be negative in order

that the exponential f u nct ion e

2iπνt

decay fast enough to ap ply Jordan’s second lemma. In

this case, the integrand has no pole inside the contour, and the residue theorem l eads to the

conclusion that G

(ret)

(t) = 0. If, o n the other h and, we have t > 0, then we integ rate from

above, and the residue at each pole must be c omputed; this is left as an exercise for t h e reader,

who will be able to check that this leads to th e same result as previously stated.

In the following, the integration will be executed sy stematically using the method of

residues.

Similarly, we will deﬁne

(ad)

(ν)

def

= lim

ǫ→0

4π ω



ν + ν

+ iǫ

−

ν −ν

+ iǫ



or, equivalently

(ad)

(ν) =

4π ω



ν + ν

−iπ δ(ν + ν

) −pv

ν −ν

+ iπ δ(ν −ν

)



which now corresponds to the integration contour

(ad)

(t)

given by the path

−−−−−−−−→

−ν

As b efore we compute the inverse Fourier transform of

(ad)

, and get

(ret)

(t) =

H (t) sin(ω

and

(ad)

(t) =

−1

H (−t) sin(ω

t).

A pedagogical example: the harmonic oscillator 413

If we chose to take α = β = 0, we obtain the average of the two preceding

Green functions, namely,

(s)



(ret)

(ad)



(where “s” stands for “symmetric”). Looking separately at t > 0 and t < 0,

this has a more compact expression:

(s)

(t) =

sin



|t|



So we have three distinct possibilities for a Green function of the harmonic

oscillator — the reader is invited to check by hand that all three do satisfy

the equation G

′′

+ ω

G = δ. The function G

(ret)

has support bounded

on the left — it is the causal, or retarded, Green function. G

(ad)

has support

bounded on the right, and is the advanced Green function. As for G

(s)

, its

support is unbounded and belongs to no convolution algebra (in particular,

its convolution product with itself is not deﬁned), which explains why it did

not come out in earlier chapters, although it is no less interesting than the

others.

The retarded Green function is the most useful. Indeed, if a harmonic

oscillator which is initally at rest (for t = t

), with pulsation ω

, is submitted

to an excitation f (t) which is zero for t < t

(the function f is then an

element of the convolution algebra D

′

), the length y of the oscillator satisﬁ es

∀t ∈ R y

′′

(t) + y(t) = f (t),

the solution of which, taking initial conditions into account, is

y = G

(ret)

∗ f ,

that is,

y(t) =

f (s) G

(ret)

(t − s) ds.

Remark 15.3 Other complex-valued Green functions can also be deﬁned. Those are of limited

interest as far as classical mechanics is concerned, by are very useful in quantum ﬁeld theory

(see the Feynman propagator on page 431).

414 Green functions

15.3

Electromagnetism and the d’Alember tian operator

DEFINITION 15.4 The d’Ale mbertian operator or simply d’Ale mbertian is

the differential operator



def

= △−

∂

∂ t

(Certain authors use a different sign convention.)

15.3.a Computation of the advanc ed and retarded

Green functions

We assume known the charge distribution ρ( r, t) and the current distribut ion

j( r, t), and we want to ﬁnd th e electromagnetic ﬁelds produced by those

distributions, up to a free s olution. The easiest method is to start by looking

for the potentials ϕ( r, t) and A( r, t) which, in Lorenz gauge, are related to the

sources by the following second order partial differential equation:

−







ρ/ǫ



. (15.4)

Hence we start by ﬁnding the Green function associated to the d’Alembertian,

that is, a the distribution G( r, t) satisfying the same differential equation

with a source δ( x) δ(t) which is a Dirac distribution, in both space and time

aspects:

−G( r, t) = δ( r) δ(t) (15.5)

(Green function of the d’Alembertian).

Put A( r, t)

def



ϕ( r, t), A( r, t)



and j( r, t)

def



ρ( r, t), j( r, t)



. The general

solution of (15.4) is given by

A( r, t) = [G ∗j]( r, t) =

ZZZ

+∞

−∞

G( r − r

′

, t − t

′

) j( r

′

, t

′

) dt

′

(up to a free s olution).

Passing to the Fourier transform in equation (15.3.a) with the convention

G ( k, z)

def

ZZZZ

G( r, t) e

−i(k·r−zt)

r dt for all k ∈ R

and z ∈ R,

Notice the sign in the exponential; this convention is customary in p hysi cs.

Electromagnetism and the d’Alembertian operator 415

An illegitimate son abandoned in front of the Saint-Jean-le-Rond

Church, the young Jean le Rond d’Alembert (1717—1783) studied

in Jesuit schools and directed his attention to mathematics. Fond

of success in the salons, he was interested in Newton’s t heories,

then much in vogue. He collaborated with Diderot to edit and

write the Encyclopédie; in particular, writing the Discours prélimi-

naire and many scientiﬁc articles. He studied complex analysis,

the equation of vibrating strings, and probability theory, and gave

the ﬁrst essentially complete proof o f the fundamental theorem

of algebra (any polynomial with real c oeffecients can be factor-

ized into polynomials of degree 1 or 2), which was completely

proved by Gauss.

we obt ain the relation

−



− k



G ( k, z) = 1.

A possible solution to this equation is

G ( k, z) =

− z

which leads, after performing the inverse Fourier transform, to

G( r, t) =

(2π)

ZZZZ

− z

i(k·r−zt)

k dz. (15.6)

However, this integral is not well deﬁned, because the integrand has a pole.

To see what happens, we start by simplifying the expression by means of an

integration in spherical coordinates wh ere the a ngular components can be

easily dealt with. So we use spherical coordinates on the k-space, putting

k = k

sin θ dk dθ dϕ, with the polar a xis in the direction of r . We have

To avoid sign mistakes or missing 2π factors, etc, use the following method: start from

the relation −G = δ, multiply by e

−i( k·r−zt)

, then integrate. Then a further integration by

parts leads to the equation above.

We know that there exist distributions (“free solutions”) satisfyi ng



− k



T ( k, z) = 0,

as, for instance, T ( k, z) = δ

( k) δ(z) or T ( k, z) = ψ( k, z) δ(z

− k

). Adding these to the

general solution changes in particular the behavior (decay) at inﬁnity; in general, the solution

will decay at inﬁnity if its Fourier transform is sufﬁciently “regular.”

416 Green functions

therefore

G( r, t) =

(2π)

ZZZZ

− z

i(kr cos θ−z t)

sin θ dk dθ d ϕ dz

4π

+∞

sin(kr)



+∞

−∞

− z

−izt



dk.

For the evaluation of the integral in parenth eses, there is the problem of the

pole at z = ±ck. To s olve this difﬁculty, we move to the complex plane

(that is, we consider that z ∈ C), and avoid the poles by deforming the

contour of integration. Different choices are possib le, leading to different

Green functions.

Remark 15.5 It is important to realize that, with the method followed up to now,

there is an ambiguity in (15.6). The ways of deforming the contour lead to radically

different Green functions,

since t hey are deﬁned by different integrals. These functions

differ by a free solution (such that  f = 0). The solution is the same as i n the

preceding section concerning the harmonic oscillator: take the principal value of the fraction at

issue, or this principal value w ith an added Dirac distribution ±iδ at each pole.

We w ill make two choices, leading to functions which (for reasons t hat

will be clear at the end of the comput ation) will be named G

(ad)

( r, t) and

(ret)

( r, t):

(ad)

( r, t)

given by the path

−−−−−−−−→

−ck ck

and G

(ret)

( r, t)

given by the path

−−−−−−−−→

−ck ck

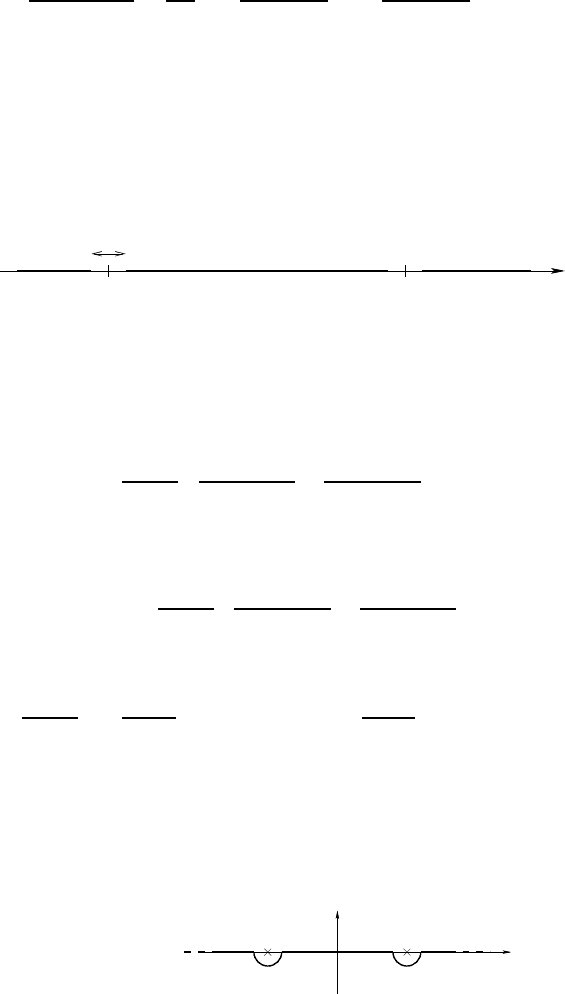
First, we compute the retarded Green function. For negat ive values of the

time t, the complex exponential e

−izt

only decays at inﬁnity if the imaginary

part of z is positive; h ence, to be able to a pply the second Jordan lemma, we

must close the contour in the upper half-plane (see page 120):

ck−ck

R → +∞

Radically different for a physicist. Some may be causal while some oth ers are not, for

instance.