Антонов В.Ф. Практикум по биофизике
Подождите немного. Документ загружается.


нат — уровень внутриглазного давления (у). Тогда каждой па-
ре значений х и у на графике
будет
соответствовать определен-
ная
точка (см. рис. 1). По характеру расположения точек мож-
но
предположить существование линейной корреляционной
зависимости
между
х и у.
Для оценки тесноты связи вычислим коэффициент линей-
ной
корреляции г по формуле (8), с
учетом
(9):
1
х = (19,8 + 7,8 + ... + 6,1) = 12,64
13
1
у=
(32,5+ 16,1 + ... + 21,4) = 21,49
1о
з-
1
13
(19,8
2
+ 7,8
2
+ ... + 6Д
2
) = 180,5
1
у
2
= (32,5
2
+ 16,1
2
+ ... +
21,4
2
)
=
482,2
_ 1
ху = (19,8 • 32,5 + 7,8 • 16,1 + ... + 6,1 • 21,4) =
283,9
13
с
х
= V 180,5 — (12,64)
2
= 4,55
о
у
= V
482,2
—(21,49)
2
= 4,51
283,9
— 12,64 • 21,49
г = =0,593
4,55-4,51
Пользуясь таблицей градации оценки тесноты связи, дела-
ем вывод: связь у с х положительная, умеренная. По формуле
(11) находим коэффициент регрессии:
4,51
p
vx
=
0,598
=
0,593
ух
4,55
Далее, подставляя его в формулу (10) и выражая у, запишем
уравнение регрессии в виде:
у =
0,593х
+ 14.
Наконец,
вычисляем ожидаемое значение у при х = 18:
у(18) =
0,593
• 18 + 14 = 24,7.
241

Выполнение
работы
Используя экспериментальные данные (по указанию препо-
давателя), с помощью компьютера выполните
следующие
за-
дания:
Задание
1. Методом наименьших квадратов найти пара-
метры линейной аппроксимирующей функции и построить ее
график.
Задание
2. Определить наличие и тесноту линейной корре-
ляционной
связи, найти уравнение линейной регрессии.
Варианты
экспериментальных
данных:
Вариант 1. У 10 человек были исследованы проницаемость
сосудов
сетчатки (х) и ее электрическая активность (у):
X
У
19,5
0,0
15,0
38,5
13,5
59,0
23,3
97,4
6,3
119,2
2,5
129,5
13,0
198,7
1,8
248,7
6,5
318,0
1,8
438,5
Вариант 2. У взрослых мужчин были измерены рост (х) и
вес (т):
х(см)
т (кг)
165
56
176
75
175
70
168
61
167
62
172
63
175
72
180
80
Вариант 3. Получены
следующие
данные о наибольшей мас-
се растворимого азотнокислого натрия (т) от температуры рас-
твора (t):
t(°C)
m(r)
0
66,7
4,0
71,0
10,0
76,3
15,0
80,6
21,0
85,7
29,0
92,9
36,0
99,4
Вариант 4. При измерении активности (А) у -препарата с по-
мощью газоразрядного счетчика через равные промежутки
времени (t) были получены данные:
t
(мин)
А, с-
1
0
12
2
23
4
17
6
36
8
9
10
19
12
25
14
7
16
16
18
26
242

Вариант 5. При изучении зависимости показателя прелом-
ления
(п) раствора от концентрации в нем соли (С) получены
следующие
результаты:
С
(г/смЗ)
п
0,000
1,333
0,025
1,338
0,050
1,340
0,10
1,350
0,20
1,362
0,4
1,377
0,8
1,389
5.4.
Использование
Фурье-анализа
в
задачах
медицинской
и биологической
физики
Многие
процессы, происходящие в живом организме, с ко-
торыми так или иначе имеет
дело
медицина, являются перио-
дическими.
Как известно, наряду с временными зависимостя-
ми,
представляющими собой зависимость от времени тех или
иных величин, характеризующих эти процессы, широко ис-
пользуется анализ их спектров (спектральное представление).
Этот анализ позволяет установить основные характеристики и
параметры гармонических колебаний, суммой которых и яв-
ляется
исследуемое
сложное колебание. Данный
метод
доста-
точно широко используется в медицине, например, спект-
ральный анализ сигналов ЭКГ и ЭЭГ позволяют диагностиро-
вать различные патологии.
Цель
работы:
1. Усвоить
теорему
Фурье как теоретическую основу спект-
рального анализа, познакомиться со спектральным представ-
лением различных физических процессов.
2. Уяснить различие
двух
важнейших типов спектров — ли-
нейчатого и сплошного (непрерывного).
3. Научиться проводить спектральное разложение простей-
ших сигналов.
Литература:
1.
Ремизов А.Н.
Медицинская
и
биологическая
физика.
шк.,
1996.
2.
Конспект
лекций.
3.
Данная
методическая
разработка.
М.:
Высш.
243

Подготовка
к
работе
Изучить следующие вопросы:
1. Теорема Фурье, ее формулировка, аналитическая запись.
Спектр периодического процесса.
2. Спектр гармонического колебания и его изменение в за-
висимости от изменения частоты, амплитуды и начальной фа-
зы исследуемого колебания.
3. Спектр сложного колебания, примеры.
4. Примеры линейчатых спектров: спектры гласного и со-
гласного звуков; характеристического рентгеновского и лазер-
ного излучений; спектр атома водорода.
5. Примеры сплошных (непрерывных) спектров непериоди-
ческих процессов — теплового и тормозного рентгеновского из-
лучения. Спектральные и интегральные величины, их связь.
Теоретические сведения
1.
Теорема
Фурье.
Приведем формулировку, математическую запись и графи-
ческую иллюстрацию теоремы Фурье.
Любой периодический процесс можно представить в виде
суммы гармонических колебаний, частоты которых кратны ча-
стоте сложного периодического процесса (сложного колебания).
В тех
случаях,
когда изучаемый процесс представляется не-
четной функцией, сложенной с некоторой постоянной состав-
ляющей, аналитически теорема может быть записана в
следу-
ющем виде:
x(t) =
AQ
+
Ajsi^m^t
+ ф
01
) + A
2
sm((O2t + Ф02) +
•••
2л
Частота w^ находится по формуле со^ = , где Т — период
сложного колебания x(t); коэффициенты AQ, AJ, А
2
, ... зави-
сят от конкретного вида функции x(t) и вычисляются по спе-
циальным формулам. (Каждой функции
соответствует
свой
собственный набор коэффициентов А
о
, А
1?
А
2
,.. .)
На
рис. 1 приведены графики временной зависимости для
некоторого сложного колебания (например, зависимости коор-
динаты от времени x(t)) и его спектра (рис. 2) — специального
представления процесса, выражающего в общем
случае
зави-
244
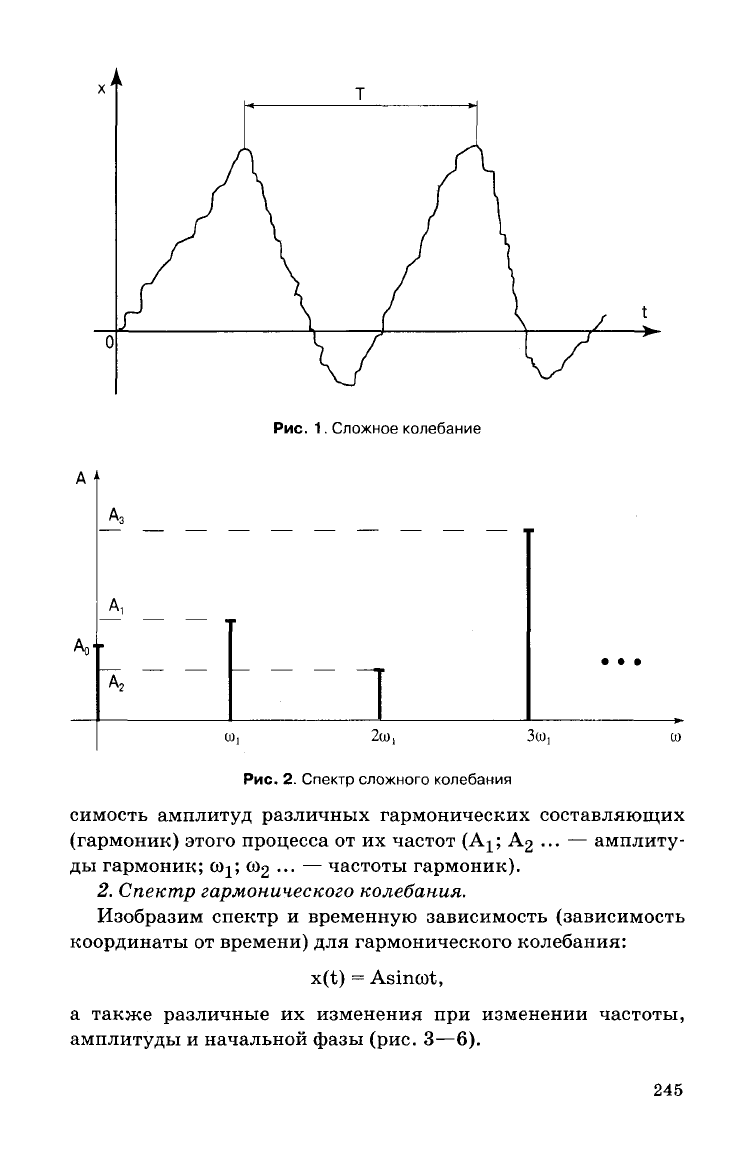
Рис.
1.
Сложное колебание
АоТ
А,
А
2
1
2ш,
Рис.
2.
Спектр
сложного
колебания
Зш,
симость амплитуд различных гармонических составляющих
(гармоник) этого процесса
от их
частот
(А^; А
2
... —
амплиту-
ды гармоник; со^;
©2
•••
—
частоты гармоник).
2. Спектр
гармонического колебания.
Изобразим спектр
и
временную зависимость (зависимость
координаты
от
времени)
для
гармонического колебания:
x(t)
=
Asincot,
а также различные
их
изменения
при
изменении частоты,
амплитуды
и
начальной фазы (рис.
3—6).
245
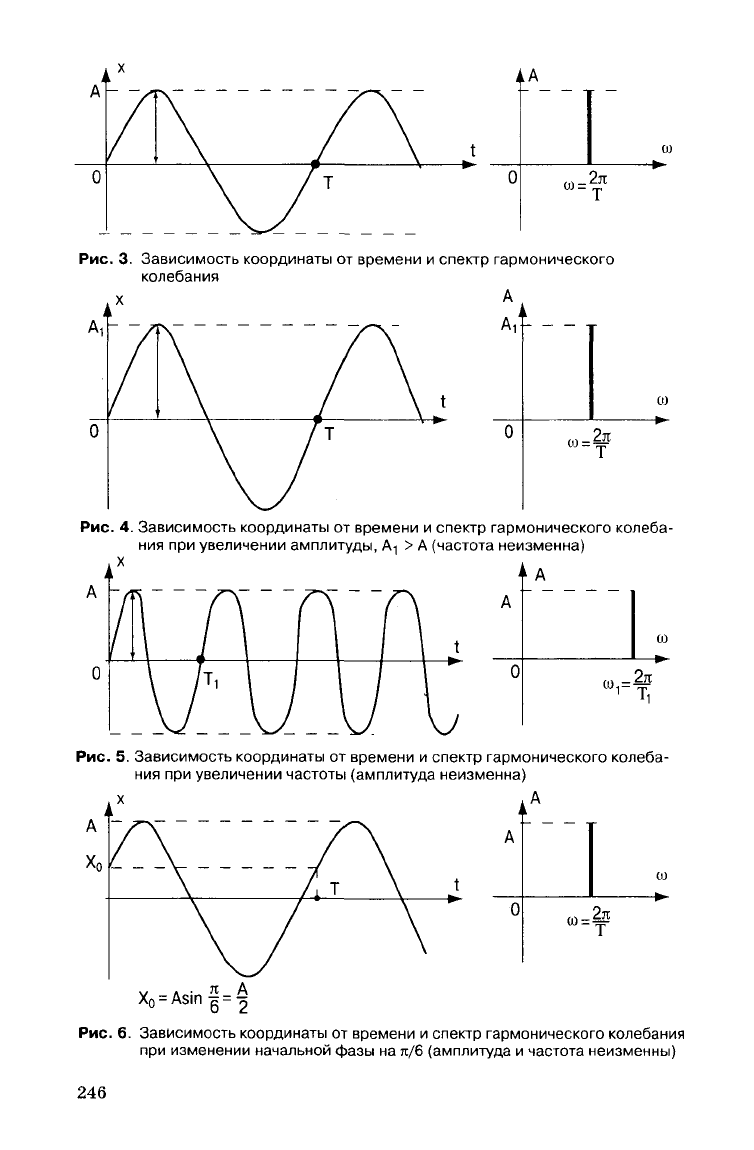
Рис. 3. Зависимость координаты от времени и спектр гармонического
колебания
Л
х
А
it i
А,
(0=^
Рис. 4. Зависимость координаты от времени и спектр гармонического колеба-
ния при увеличении амплитуды, А-| > А (частота неизменна)
х
J
А
0
^ А
03
^-
Рис. 5. Зависимость координаты от времени и спектр гармонического колеба-
ния при увеличении частоты (амплитуда неизменна)
А
А /
А
Хо
Рис. 6. Зависимость координаты от времени и спектр гармонического колебания
при
изменении
начальной
фазы
на гс/б (амплитуда и частота неизменны)
246
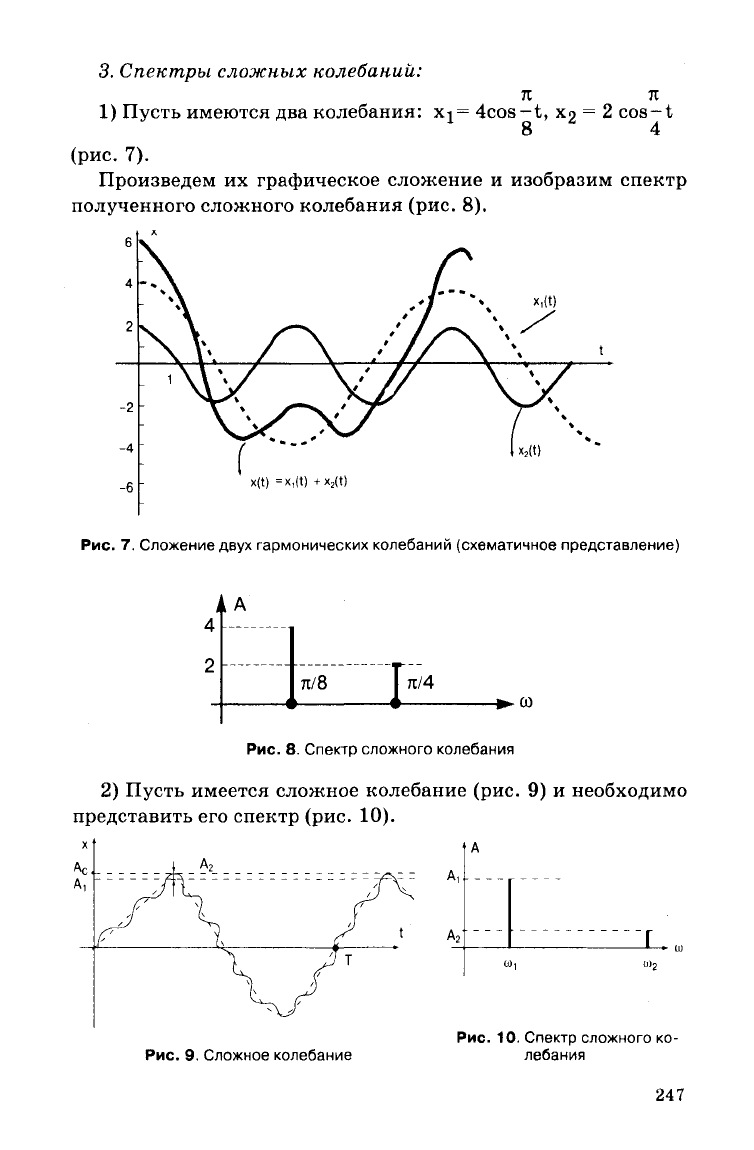
3.
Спектры
сложных
колебаний:
к п
1) Пусть имеются два колебания: xj= 4cos-t, х
2
= 2 cos-t
8 4
(рис.
7).
Произведем их графическое сложение и изобразим спектр
полученного сложного колебания (рис. 8).
x,(t)
x
2
(t)
Рис.
7. Сложение двух
гармонических
колебаний (схематичное представление)
Л/8
1
Я/4
».
(О
Рис.
8. Спектр сложного колебания
2) Пусть имеется сложное колебание (рис. 9) и необходимо
представить его спектр (рис. 10).
X
Ас,
А,
1
А
2
S
(Г
'
Рис.
9. Сложное колебание
Рис.
10. Спектр сложного ко-
лебания
247
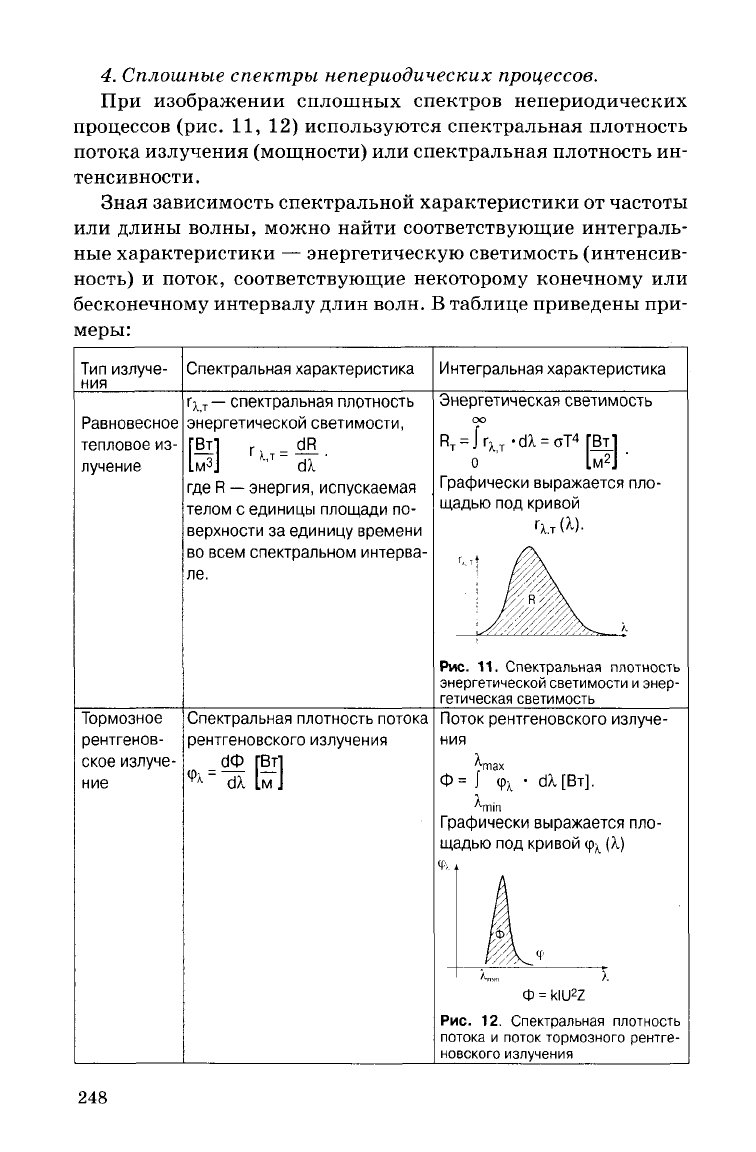
4. Сплошные
спектры
непериодических процессов.
При
изображении сплошных спектров непериодических
процессов (рис.
11, 12)
используются спектральная плотность
потока излучения (мощности)
или
спектральная плотность ин-
тенсивности.
Зная
зависимость спектральной характеристики
от
частоты
или длины волны, можно найти соответствующие интеграль-
ные характеристики
—
энергетическую светимость (интенсив-
ность)
и
поток, соответствующие некоторому конечному
или
бесконечному интервалу длин волн.
В
таблице приведены при-
меры:
Тип излуче-
ния
Спектральная характеристика
Интегральная характеристика
Равновесное
тепловое
из-
лучение
г\
т
— спектральная плотность
энергетической
светимости,
Г
*=
Энергетическая
светимость
оо
О
rBTl
l
M
2j
•
где
R —
энергия, испускаемая
телом
с
единицы площади
по-
верхности
за
единицу времени
во всем спектральном интерва-
ле.
Графически выражается
пло-
щадью под кривой
Рис.
11.
Спектральная плотность
энергетической
светимости
и
энер-
гетическая
светимость
Тормозное
рентгенов-
ское
излуче-
ние
Спектральная плотность потока
рентгеновского
излучения
ф
*~
ей LM
Поток
рентгеновского излуче-
ния
Ф=
I
ей
[ВТ].
n
Графически выражается
пло-
щадью
под
кривой
ф^
(К)
Ф
=
klU
2
Z
Рис.
12.
Спектральная плотность
потока
и
поток тормозного рентге-
новского
излучения
248

Выполнение
работы
Работа выполняется на ПЭВМ. Головное меню состоит из 10
пунктов. К кадру, содержащему это меню, вы
будете
возвра-
щаться каждый раз после выполнения того или иного пункта.
Используя клавишу >U , вы можете перейти к следующему
пункту. Порядок нажатия клавиши в процессе выполнения за-
дания
в каждом из пунктов
будет
понятен — на экране имеют-
ся
соответствующие указания. Выбирая меню, выполните за-
дания.
Задание
1. Ознакомление с теоретическими сведениями.
Нажав
клавишу "ENTER", внимательно прочтите краткие
вводные теоретические сведения, обратив внимание на анали-
тическую запись теоремы Фурье, а также на то, как соотносят-
ся
частоты гармоник, на которые разложен сложный периоди-
ческий
сигнал, какой частоте они кратны, как ее найти.
Задание
2. Сложение гармонических колебаний.
а) Пронаблюдайте графическое сложение
двух
гармоничес-
ких колебаний разных частот и амплитуд. Зарисуйте в тетради
графики,
представляющие зависимость координаты колеблю-
щегося тела от времени в обоих
случаях,
а также график, на
котором представлена зависимость y(t) для суммарного коле-
бания.
Зарисуйте также спектр суммарного колебания.
б) Пронаблюдайте процесс сложения
трех
различных гар-
монических колебаний. Зарисуйте в тетради временную зави-
симость и спектр полученного в
результате
сложного колеба-
ния.
Задание
3. Сложение произвольных гармонических колеба-
ний.
Введите с клавиатуры значения амплитуд и частот
трех
гар-
монических колебаний (они должны находиться в тех интер-
валах,
которые указаны на экране, но так, чтобы частоты
всех
трех
колебаний различались), пронаблюдайте их временные и
спектральные зависимости.
Пронаблюдайте сложение
двух
колебаний, а затем
трех.
По-
сле получения последней временной зависимости нарисуйте
249

самостоятельно в тетради спектр полученного сигнала. Про-
верьте правильность Вашего ответа, нажав ^aBHiny"ENTER".
Задание
4. Спектральное разложение прямоугольного им-
пульса.
а) После получения на экране временной зависимости на-
жмите еще раз клавишу "ENTER" и пронаблюдайте времен-
ную зависимость y^(t) для первой гармоники. Чему равна ее
частота? Согласуется ли это с теоремой Фурье?
б) Какую частоту должна иметь вторая гармоника? Ответ
проверьте, нажав клавишу "ENTER" и получив временную за-
висимость для второй гармоники.
в) После получения последней гармоники пронаблюдайте
решение компьютером задачи, обратной задаче спектрального
разложения — задачи последовательного сложения времен-
ных зависимостей, соответствующих каждой из гармоник Фу-
рье — разложения исследуемого сигнала. Обратите внимание
на
то, как по мере увеличения числа складываемых гармоник
графический
результат
все точнее приближается по форме к
прямоугольному импульсу (тому сигналу, который первона-
чально подвергался Фурье-разложению).
г) Зарисуйте в тетрадь временную зависимость и спектр
прямоугольного импульса.
Задание
5. Спектральное разложение треугольного им-
пульсного сигнала.
а) После получения на экране временной зависимости на-
жмите еще раз клавишу "ENTER" и пронаблюдайте времен-
ную зависимость y^(t) для первой гармоники. Чему равна ее
частота? Согласуется ли это с теоремой Фурье?
б) Какую частоту должна иметь вторая гармоника? Ответ
проверьте, нажав клавишу "ENTER" и получив временную за-
висимость для второй гармоники.
в) После получения последней гармоники пронаблюдайте
решение компьютером задачи, обратной задаче спектрального
разложения — задачи последовательного сложения времен-
ных зависимостей, соответствующих каждой из гармоник Фу-
рье-разложения исследуемого сигнала. Обратите внимание на
то,
как по мере увеличения числа складываемых гармоник
260
