Антонов В.Ф. Практикум по биофизике

Подождите немного. Документ загружается.

Дх — мал. Прямоугольники гистограмм

будут

узкими, и число

их

будет

велико. Ступенчатая линия гистограммы станет мало

отличаться от плавной кривой, которая и

будет

являться

функцией

у = f(x), указывающей чему равна ордината у, соот-

ветствующая заданной абсциссе х. Приближенно предполагае-

мый

вид функции ПРВ показан на рис. 6 пунктирной линией.

Кроме

этого представление экспериментальных данных имен-

но

в виде гистограммы плотности относительных частот необ-

ходимо, если ставится задача, например, о сравнении вида рас-

пределений

двух

или нескольких совокупностей. В этом слу-

чае бывает полезным совмещение различных гистограмм, а

это

возможно только, если рассматриваются плотности отно-

сительных частот, что позволяет исключить зависимость от

объема выборки и ширины интервала Ах. Так, в клинической

практике

часто приходится сравнивать разные группы паци-

ентов,

например: здоровые и больные, принимающие лекарст-

во и не принимающие и т.п., причем, количество пациентов в

сравниваемых группах, как правило, не одинаково (48 здоро-

вых и 21 больной). В этом

случае

для сравнения можно пользо-

ваться только гистограммой плотности относительных частот.

Если

же взять гистограммы плотности частот, то высоты

столбцов для здоровых (48) и больных (21)

будут

заведомо не

одинаковы.

При

построении гистограммы весьма важно правильно вы-

брать ширину интервала Ах. Если число интервалов "к"

будет

мало (ширина интервала Ах — велика),

следует

ожидать, что

частично информация о случайной величине может быть по-

теряна. С

другой

стороны, если "к"

будет

слишком велико (Ах

— мало), обработка результатов измерений

будет

излишне тру-

доемкой, не давая при этом существенного выигрыша

инфор-

мации.

Практика показывает, что рационален выбор числа ин-

тервалов "к" в зависимости от объема выборки с помощью таб-

лицы:

Объем

выборки (п)

Число интервалов (к)

25-40

5-6

40-60

6-8

60-100

7-10

100-200

8—12.

200

10-15

Для более наглядного сравнения нескольких гистограмм

(например,

при сравнении физиологических данных в норме

221

при патологии) их необходимо строить одну под

другой

в од-

ном

масштабе как по горизонтальной, так и по вертикальной

оси.

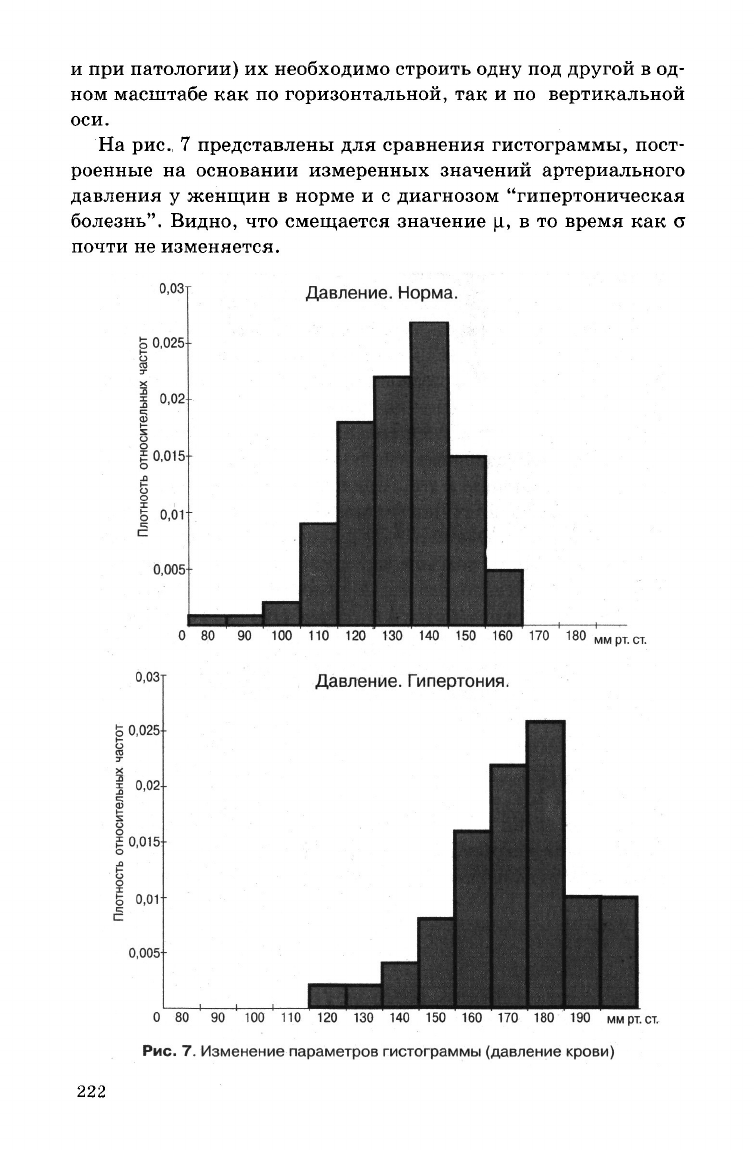
На

рис. 7 представлены для сравнения гистограммы, пост-

роенные

на основании измеренных значений артериального

давления у женщин в норме и с диагнозом "гипертоническая

болезнь". Видно, что смещается значение ц, в то время как а

почти не изменяется.

0,03т

; 0,025

Давление.

Норма.

0 80 90 100 110 120 130 140 150 160 170 180

Давление.

Гипертония.

мм

рт. ст.

0,03]

;

0,025

0,02

; 0,015

0,01

0,005

80 90 100 110 120 130 140 150 160 170 180 190 ммрт.ст.

Рис.

7. Изменение параметров

гистограммы

(давление крови)

222

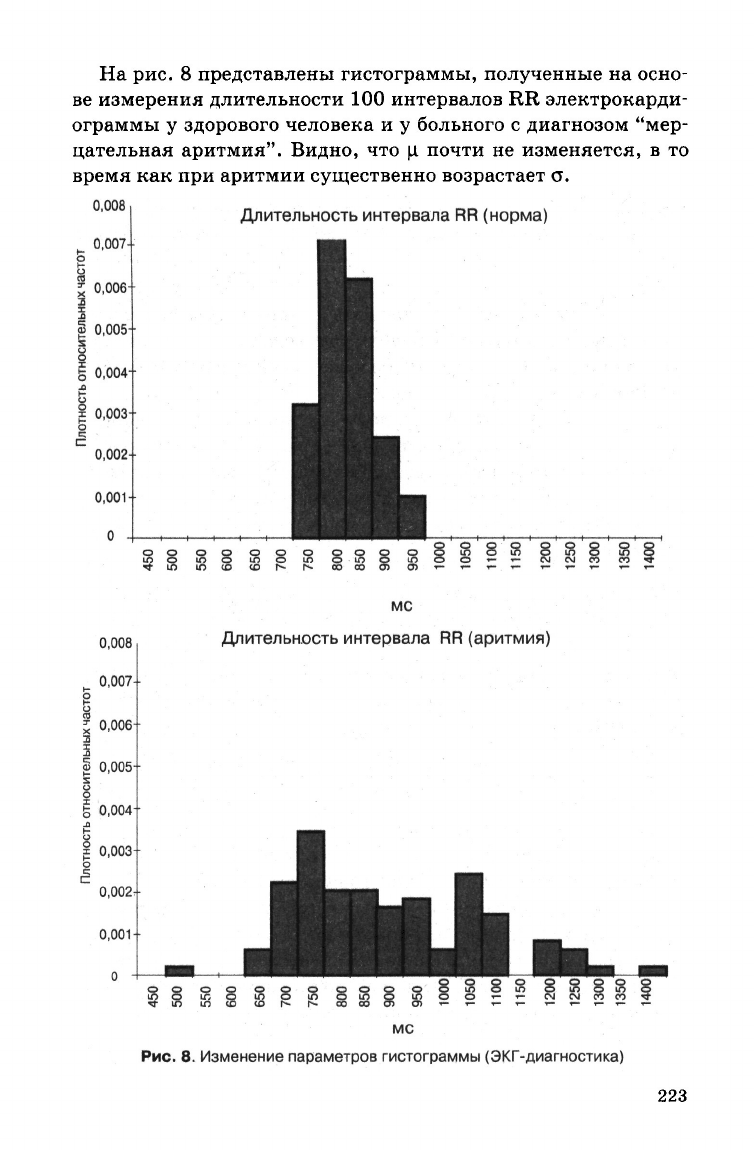
На

рис. 8 представлены гистограммы, полученные на осно-

ве измерения длительности 100 интервалов RR электрокарди-

ограммы у здорового человека и у больного с диагнозом "мер-

цательная аритмия". Видно, что ц почти не изменяется, в то

время как при аритмии существенно возрастает а.

Длительность

интервала RR (норма)

S S

мс

Длительность

интервала RR (аритмия)

мс

Рис.

8. Изменение параметров

гистограммы

(ЭКГ-диагностика)

223

Выравнивание

(сглаживание)

статистических

рядов.

При

обработке статистического материала часто приходит-

ся

решать вопрос о том, как подобрать для данного статис-

тического ряда теоретическую кривую распределения, вы-

ражающую лишь существенные черты статистического ма-

териала, но не случайности, связанные с недостаточным

объемом экспериментальных данных. Такая задача называ-

ется задачей выравнивания (сглаживания) статистических

рядов.

Задача сглаживания заключается в том, чтобы подобрать

теоретическую плавную кривую распределения, с той или

иной

точки зрения наилучшим образом описывающую данное

статистическое распределение.

Допустим величина А подчиняется нормальному закону.

Тогда задача сглаживания переходит в

задачу

о рациональном

выборе параметров ц и а в законе

Гаусса.

Из теории известно,

что прежде всего необходимо вычислить среднее выборочное

значение

(х

), определяемое для непрерывной случайной ве-

личины

по формуле:

mi -х* +

*x*

+ ...+ mi. -x,* 1 v

nij + ni2 +...+ ГЛ]^ n i=\

где

mj,

ГП2,

... , m^ —

частоты

соответствующих интервалах,

Х]\

Х2> ..., xjj —

середины интервалов, которые вычисляются

по

формулам:

2 ,

к-1

у* =

* — .

k ~

су

Zi су К су

Термин

"выборочное" означает, что среднее значение вы-

числяется по данной группе (например, по группе больных,

включающей 22 пациента), называемой выборкой.

Кроме

среднего выборочного значения случайную величину

характеризуют параметром, показывающим насколько широ-

ко

разбросаны отдельные значения случайной величины отно-

сительно среднего значения, так называемым выборочным

средним квадратическим отклонением о

224

в)

(x*-x

)

+...+

(x*-x

)

Поясним

сказанное примером.

Пользуясь данными вышеуказанной таблицы, вычислить

ио-

10+ 15

Вычислим середины интервалов: Xi = = 12,5, ... ,

30 + 35

= —

=32,5.

Подставляя найденные значения и соответствующие часто-

ты в формулы (1), (2), получаем:

•

12,5 + 4

•

17,5 + 8

•

22,5 + 4

•

27,5 + 2

•

32,5

= = 22,5

2+4+8+4+2

2(12,5-22,5)

+4(17,5-22,5)

+8(22,5-22,5)

+4(27,5-22,5)

+2(32,5-22,5)

О„=

=5,5

\ 20

Напишем

выражение нормального закона в этом

случае:

(х-22,5)

5,5л/2л

Построим

на одном графике и гистограмму, и выравниваю-

щую ее кривую (рис. 6).

Выполнение

работы

Все задания выполняются на ПК с помощью стандартных

пакетов программ, например, "Statgraph",

"Excel"

и др.

Задание

1. Проведите анализ кривых распределения слу-

чайной

величины по нормальному закону.

225

Для этого:

1) Запишите закон

Гаусса

для

заданных параметров

ц и о.

2) Постройте графики (выберите масштаб, отложите

по

осям

величины

единицы

их

измерения). Сделайте вывод

влиянии

и а на

положение

форму кривой распределения.

3) Вычислите интервал

За,

куда

попадают практически

все

случайные величины. Покажите

его на

графике.

Варианты изменения

|Д и а

представлены

таблицах:

а)

женщины

мужчины

б)

Ц.

г/л

140

158

о,

г/л

6.6

6.8

В таблице

в)

указано содержание гемоглобина

крови (дан-

ные

из

учебника "Физиология человека"

под ред. Р.

Шмидта)

Задание

Постройте

проанализируйте гистограммы

плотности относительных частот. Проведите

их

выравнива-

ние,

считая закон распределения нормальным.

Варианты

данных измерения

длительности

интервалов

RR.

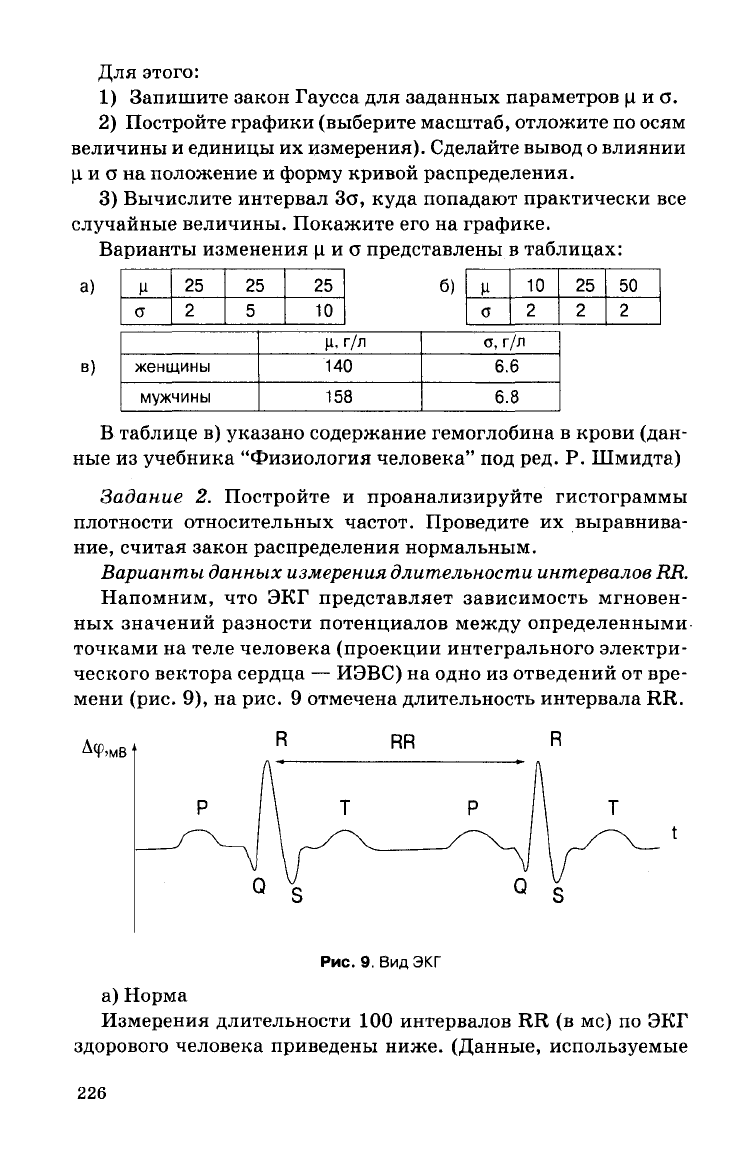
Напомним,

что ЭКГ

представляет зависимость мгновен-

ных значений разности потенциалов

между

определенными-

точками

на

теле

человека (проекции интегрального электри-

ческого вектора сердца

—

ИЭВС)

на

одно

из

отведений

от вре-

мени

(рис.

9), на

рис.

отмечена длительность интервала

RR.

Дф,

мВ

Рис.9.

Вид ЭКГ

а) Норма

Измерения

длительности

100

интервалов

RR (в мс) по ЭКГ

здорового человека приведены ниже. (Данные, используемые

226

в заданиях а, б, в, г любезно предоставлены к.мед.н., с.н.с.

ММА им. И.М. Сеченова Э.М. Кутерманом.)

(мс):

787

943

843

887

764

841

743

864

798

743

778

706

845

730

773

801

868

826

896

802

836

819

777

755

780

790

718

791

740

746.

869

918

826

802

839

799

788

816

807

799

734

744

755

749

923

881

763

816

822

824

792

734

741

823

788

827

828

808

872

771

775

925

831

799

752

757

764

757

832

730

773

829

764

827

873

854

762

773

732

850

799

815

801

753

793

894

822

907

883

857

755

757

769

805

775

748

728

775

821

824

б) Мерцательная аритмия

Измерения

длительности 100 интервалов RR (в мс) по ЭКГ

больной с диагнозом "Мерцательная аритмия" приведены ниже:

(мс):

676

1051

741

861

902

876

1085

881

1200

812

1249

1046

1175

1001

1219

793

1074

1020

802

668

1268

753

950

1016

946

691

760

903

723

985.

827

846

805

844

948

980

758

854

1028

882

697

1075

856

631

734

757

875

715

727

861

773

902

660

742

1047

843

725

1169

955

921

712

743

681

748

772

718

715

911

1034

844

1018

708

730

856

1036

651

774

819

1086

646

809

797

690

681

741

739

489

785

928

1075

698

637

1376

1156

1025

1078

789

743

1209

690

Мерцательная аритмия возникает обычно в

результате

мер-

цания

предсердий (мерцания

желудочков

несовместимы с

жизнью, и

требуются

срочные реанимационные меры, вклю-

чая дефибрилляцию), при котором общая систола предсердий

227

заменена беспорядочным возбуждением и сокращением от-

дельных групп мышечных волокон. При мерцании предсер-

дий желудочковые сокращения аритмичны. Часть сердечных

сокращений,

при слабом наполнении желудочков, неэффек-

тивны,

то есть сопровождаются малым сердечным выбросом и

отсутствием пульсовой волны. В

результате

этого число сер-

дечных сокращений

будет

больше, чем число пульсовых волн

(дефицит пульса). Отрицательное воздействие на кровообра-

щение

при мерцательной аритмии обусловлено выпадением

сокращений

предсердий, что уменьшает наполнение

желудоч-

ков,

а также нарушением желудочкового ритма.

в) Синусовая тахикардия

Измерения

длительности 100 интервалов RR (в мс) по ЭКГ

больной с диагнозом "Синусовая тахикардия" (больная на 1-е сут-

ки

после нейрохирургического вмешательства) приведены ниже:

(мс):

500

496

492

488

492

496

492

484

488

492

496

492

488

492

496

488

492

496

484

484.

492

488

492

496

492

484

496

492

488

492

496

488

496

488

496

492

488

492

496

488

496

492

488

492

496

492

496

488

500

496

488

492

488

492

496

492

488

492

Синусовая тахикардия в условиях патологии встречается

при

интоксикациях, шоке, неврастении и т.д. Синусовая тахи-

кардия

сопровождается увеличением числа сокращений серд-

ца

от 90 и более в минуту.

г) Желудочковая экстрасистолия

Измерение

длительности 100 интервалов RR в мсек по ЭКГ

больной с диагнозом "Желудочковая экстрасистолия" (боль-

ная

на 6-е сутки после нейрохирургического вмешательства)

приведены ниже.

228

(мс):

720

728

740

424

736

700

708

712

716

720

744

736

760

724

728

420

1096

732

728

692

708

724

420

728

764.

720

440

1096

760

736

748

720

688

704

720

732

740

1080

744

420

1044

776

728

748

736

404

676

708

728

1452

744

740

748

1004

752

736

744

748

736

1028

680

716

416

732

748

724

744

728

748

740

736

748

736

716

688

724

1028

716

744

728

748

724

740

744

728

736

704

696

720

728

732

736

752

Экстрасистолия

характеризуется преждевременным воз-

буждением и сокращением сердца в

результате

появления

дополнительного очага повышенной возбудимости в сердеч-

ной

мышце. (Уточнение локализации очага возбуждения

(предсердия,

желудочки) возможно только при электрокар-

диографическом

исследовании.) После такого преждевре-

менного

сокращения очередной импульс, возникающий в

синусовом узле, не реализуется, и поэтому

следует

более

длинная

пауза, которую больные нередко ощущают как "за-

мирания",

перебои в работе сердца. Экстрасистолы

могут

возникать

при

всех

органических заболеваниях сердца,

прежде всего при ишемической болезни, пороках и т.д., но

могут

наблюдаться и без органической патологии, прежде

всего при неврастении.

Все гистограммы плотности относительных частот в задани-

ях а—г необходимо построить в одном масштабе,

друг

под дру-

гом.

Вычислите среднее выборочное значение х

и выборочное

среднее квадратическое отклонение а

. Проведите сглажива-

ние

гистограмм с помощью функций нормального распределе-

ния.

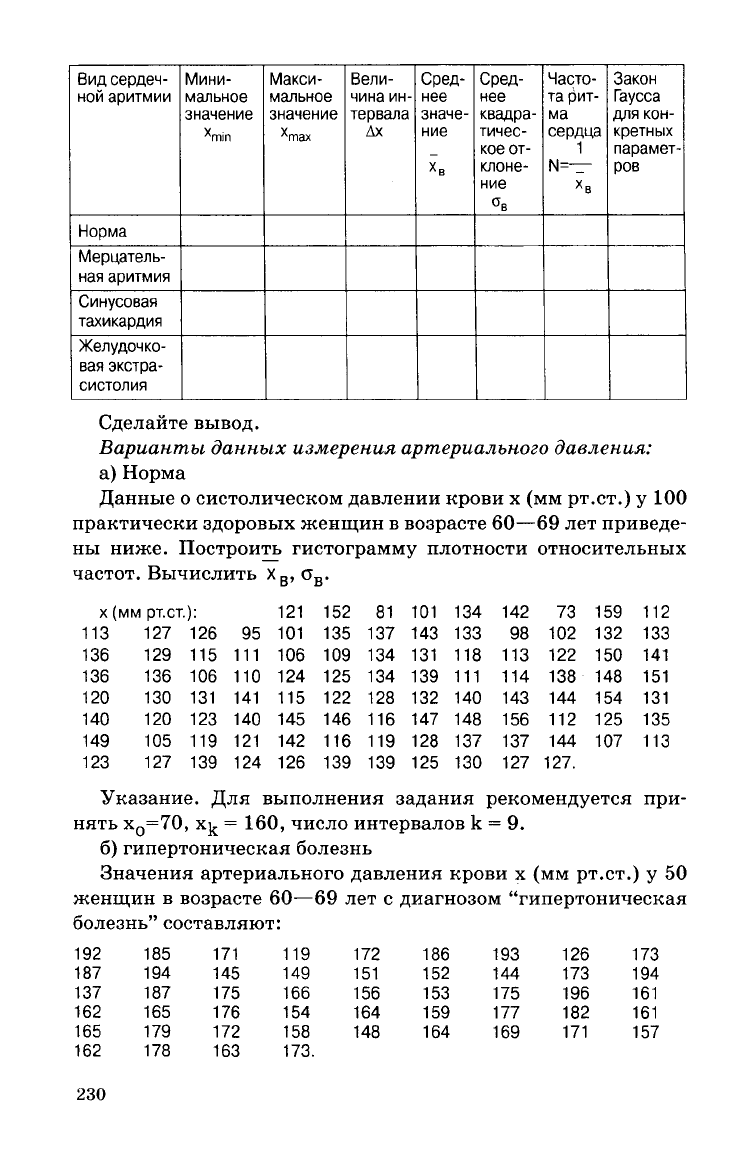
Для сравнения данных некоторых сердечных аритмий с

данными

в норме заполните таблицу:

229

Вид

сердеч-

ной аритмии

Норма

Мерцатель-

ная аритмия

Синусовая

тахикардия

Желудочко-

вая экстра-

систолия

Мини-

мальное

значение

min

Макси-

мальное

значение

тах

Вели-

чина

ин-

тервала

Дх

Сред-

нее

значе-

ние

Хв

Сред-

нее

квадра-

тичес-

кое

от-

клоне-

ние

°в

Часто-

та

рит-

ма

сердца

N=—

Закон

Гаусса

для

кон-

кретных

парамет-

ров

Сделайте вывод.

Варианты

данных измерения

артериального

давления:

а) Норма

Данные

систолическом давлении крови

х (мм

рт.ст.)

у 100

практически здоровых женщин

возрасте

60—69

лет

приведе-

ны

ниже. Построить гистограмму плотности относительных

частот. Вычислить

<т

(мм

рт.ст.):

113

127 126

136

120

140

149

123

129

115

136

106

130

131

120

123

105

119

127

139

121

101

111

106

110

124

141

115

140

145

121

142

124

126

152

135

137

109

134

125

134

122

128

146

116

119

139

101

134

143

133

131

118

139

111

132

140

147

148

128

137

125

130

142

102

113

122

114

138

143

144

156

112

137

144

127

127.

159

112

132

133

150

141

148

151

154

131

125

135

107

113

Указание.

Для

выполнения задания рекомендуется

при-

нять

=70,

xjj = 160,

число интервалов

к = 9.

б) гипертоническая болезнь

Значения

артериального давления крови

х (мм

рт.ст.)

у 50

женщин

возрасте

60—69

лет с

диагнозом "гипертоническая

болезнь" составляют:

192

187

137

162

165

162

185

194

187

165

179

178

171

145

175

176

172

163

119

149

166

154

158

173.

172

151

156

164

148

186

152

153

159

164

193

144

175

177

169

126

173

196

182

171

173

194

161

157

230