Ames W.F., Roger C. Nonlinear equations in the applied sciences. Volume 185
Подождите немного. Документ загружается.


160
Andrea
Donato
where, in order
to
have
a
translation, we require
(C4)r
=
1
(C4t
=
0
(44)
(<*a)rA
=
0
These represent
a
system of differential equations
to
determine the
canonical variables
t,
r
and
WA.
The method of characteristics produces the solution in the form
r=/
dt
T[x(t,
6,
w1,
-
- -
3
WN),
t, UA(t,
0,
w1,
-
-
*
,wN)]
t
=
t(~,Wl,...,Wv)
(45)
WA
=
w~(u,wi,...,W~)
where the parameters
u,
W1,
.
.
.,
WN
are obtained by integration of
the characteristic equations:
duN
=
-
(46)
A
possible choice of canonical variables rendering the group
G
a
dr
dUl
-
-
...
=
- -
dt
- -
dx
“9
t,
4
T(x, t,
u)
Vl(Z,
t,
4
VN(X,t,U)
1
.r-translation is:
For
instance, if the group
G
is the dilatation group having gen-
erators
T
=
72
x=x
VA
=
aAUA
with
QA
and
7
#
1
suitable constants, then the canonical variables
are:
1
7
r
=
-1nt

Nonlinear Waves
161
(49)
We remark that, by expressing the system
36
in terms of canonical
variables the solutions depending only on
t
are, infact, the invariant
solutions with respect to the group
G
since the invariance condition
is
Let us consider now the case when the system
36
is invariant with
respect to the dilatation group. In such
a
case
F(u)
and
B(u,z,t)
must satisfy restrictions in their functional forms. These have been
determined in
[24].
Thus, if we assume that at least one
of
the
C~A
is different from zero, say
a1
=
a,
with the corresponding compo-
nent of
u
denoted by
u1
=
u,
the invariance requires the following
expressions for
F
and
B:
FA
=
upA/u
fA(u1,
uz,.
. .
,I,.
. .
,
UN)
(51)
BA
=
u(PA-l)/abA(ul,
u2,.
.
.
,I,.
.
,
UN,
2/u1fu,t/uy/a)
where
UA
=
uA/uaAfa,
p~
=
CUA
-
7
+
1,
A
=
1,2,.
.
.
,
N.
such that
To these relations the transformations of variables
50
is applied
whereupon
52
becomes

162
Andrea
Donato
In the new variables
50,
the governing system
36
in component
form, becomes
It is now assumed that
BA
may be written
as
In the new variables
the system
54
becomes
:
where
PA
=
FA(VA)
,
BA
=
BA(vA).
Consequently, under the assumed conditions, the transformations
53
and
56
change
36
into
57,
with independent variables that do not
appear explicitly in the coefficients. The condition
56
means that
the system
54
is
invariant with respect to the dilatation group
r*
=
7
t*
=
Pt
P
E
R
-
(0)
(58)
v:
=
p
aA/(l-'Y)
vA
Since, in
a
certain sense, this result generalizes
to
systems
of
equations the ideas
of
L.
Dresner
[20],
we call this group the
associ-
ated
group
of
the principal dilatation invariance group
for
the system
36:

Nonlinear Waves
163
In terms
of
the original variables the existence
of
the
associated
group
,
as
can be easily verified, is assured by requiring that
BA
in
52
is expressed by:
In other words the functions
&A
must be homogeneous of degree
-1
in the
last
two variables
.
In the more usual case when
BA
does not depend on
t,
the form
(4.16)
remains the same with the last variable,
a
combination
of
u,
x
and
t,
dropped.
From the relations,
50, 53
and
56
it follows that the system
36
admits
a
solution
of
the form
UA
=
(7)
uA/(l-Y)~A
(61)
provided that the
associated
group
is admitted. The similarity
so-
lutions
VOA(~)
are obtained by solving the autonomous system of
ordinary differential equations which results from
57
when the de-
pendence on
T
is omitted, namely:
There
“o”
means that
a
quantity is evaluated for
VA
=
VOA.
If the
matrix
has
N
real and distinct eigendues
KO
with the corresponding left and
right eigenvectors linearly independent, that is the governing system
is strictly hyperbolic, the system
62
may be solved with respect to
dvOA/dq
to obtain, by the Cramer rule:
AA
--
-
dvOA
d77
AA
=
BOMCMA
(f
-
iOl)($
-
iod.
-
*
(f
-
KON)
(64)

164
Andrea
Donato
where
CMA
is the transpose
of
the matrix formed with the cofactors
of
AOMC
-
6MC/7
and
-&I
,
&2,
. .
.
,
&-)N
the eigenvdues
of
&MC.
There is
a
possible singularity on
a
curve
q
=
constant
if one of the
fto
takes the value
l/7.
It is well known that singularities can occur
only through characteristics of the original system expressed by
:
dx
X-
-
=
X
=
-A0
dt t
where
X
is an eigenvalue
of
the matrix
A
in
36.
Since on
a
line
q
=
constant
we have simply
dx
x
dt yt
_-
-
-
it follows
A0
=
l/7
in order for this line to be
a
characteristic. To
avoid this discontinuity we have to require that also
AA
=
0
when
det(&
-
$1)
=
0.
From the system
62
it follows that
with
&
the left eigenvector
of
the matrix
A0
corresponding to
jo
that
can be chosen in one of the alternative forms
&A
a
CAI
O(
ci2
a
a
. .
.
a
CAN
(68)
where
CiM
is the transpose of the matrix formed with the cofactors
It can be easily seen that if one of the
10
=
$
then the corre-
sponding left hand-side of
67
is zero and, consequently, there is one
of the
AA
in
65
that is automatically zero since
of
a,
-
A01
.
The
limiting chamcteristic
where the singularity appears is char-
acterized by
a
value of
q,
say
qc,
such that exp(qc)
=
x/tY
corre-
sponding to the
Ao(v0~)
=
l/y
that makes the denominator of
65
zero.
In
order that the solution
to
be continued for value of
q
close

Nonlinear Waves
165
to
qc
,
since one
of
the
AA
is zero, it is enough to require that the
others
N
-
1
AA
are zero. In order to determine
qc
we
assume to
have at least one boundary condition associated with the system
62
(see
[20], [25])
of
the type
vol(0)
=
VO.
.I
Now we guess
a
value
ijc
and calculate
50r,(ijc)
by using det(&
-
XoI)
=
0
and
AA
=
0.
The
50r,
so
determined may be used
as
boundary conditions to integrate
the system
62
inwards to the origin
q
=
0
obtaining
50r,(O).
By the
invariance conditions we may determine
p
as
501
=
pal/(l-T)v~
and
by using
t*
=
pt
we get:
5
Wave propagation in a %on-constant state”
Here we would like to study the propagation
of
weak discontinuities,
in the field variables
vr,
compatible with the system
57
across
a
curve
@(~,q)
=
0
in
a
non-constant state characterized by
a
similarity
solution
vo~(q)
satisfying
62 [24].
This problem requires that the non-constant state, in which the
discontinuity propagates, be dependent only on one independent vari-
able called the
space
variable.
For
simplicity the system
57
studied hereafter is supposed to be
strictly hyperbolic with the characteristic velocities solutions
of
consequently, the link between the characteristic velocities
A
and the
eigenvalues
of
the matrix
a
are given by
A=7A-l
(
72)
Under these assumptions and with
&r,
=
&(vor,)
after
25
it
follows

166
Andrea
Donato
In the original variables
UA
is
given by 61 and its first derivatives
are
discontinuous across
O*(x, t)
=
@(r(t),
~(x,
t))
with
there follows
g*uA
=
(
;)aA/(1-7)6vA
(75)
Moreover
as
(76)
a
-
la
-
=
-(-
-
-)
at 7t
ar
aq
ax
xaq
-
--
-
a
la
a
there follows that
dx
X
2-
-=A=
-(A+l)=-X
.
dt Yt t
The characteristic rays associated with
57
are
r=u
r-r~=L;i;;dq
'11
(77)
so
instead
of
using
u,
the time along the rays, we may use
7
in order
to compute the discontinuity in our case given by
where
(80)
7
-dv
aft
A
ai
ai
dv
h
=
~{(1-)(-a)
+
-a((-)=
-
-)
(1d)o
dV
lh
7
av
d'l

Nonlinear Waves
167
For
what concerns
4,,,
given the initial discontinuity line &(q), after
78
,
we get
4
=
&(r
-
Ji
kd~)
so
it follows
4,,
=
-&(,.
Moreover,
we may use
65
in
81
in order
to
eliminate
2
.
In the case when
h
=
0
we have the following relation to determine the discontinuity
6
Propagation in a "constant state": physi-
cal applications
Let
VA
=
VOA
=
constant
be
a
solution
of
(82)
1
B(V~A)
=
&A
+
T(~AZ)OA
-
PA&A)
=
0
.
7-
Because of
61
this corresponds to
a
non-constant particular solu-
tion
of
the original system
36,
in fact
a
self-similar solution.
As
will
be seen, the propagation
of
weak discontinuities in the original vari-
ables in such "non-constant" states may be studied
as
a
propagation
in
a
"constant state" in the new variables. In the present special case
the characteristic rays are
r=u
V
=
710
t
ho(T
-
To)
with
&
=
constant.
As
T
=
+lnt
and
7
=
In[
=
In
&
we have
X
t
(Ao+l)/r
-
=(,I
XO
Consequently from
79,
81
there results:
To(
2)-
+
?r=
1
-
To%((&)-+
-
1)
where, without loss
of
generality, we choose
4,,
=
1
as
we are consid-
ering
a
propagation in
a
constant state.

168
Andrea
Donato
From 36 the time
tc
when the discontinuity wave evolves into
a
shock wave is given by:
-I
hot
ma0
ho
tc
=
to(
)
.oao
This occurs when the initial discontinuity is such that:
i)
lroao
>
0,
ho
>
--Iroao
ii)
.oao
<
0,
ho
<
1.0.01
*
In the case when
ho
=
0
the equation
85
must be substituted by
As
a
first physical example
[27], [28]
a
spherical symmetric motion
of
a
polytropic gas, neglecting any dissipation mechanism, is studied.
The equations of motion take the form 36 with:
-2pu
.=[:I
A=[;
PO
u
i]
B=[
[
]
(88)
o
rp
-m
where
p
is the density,
u
is the particle velocity,
p
the gas pressure,
T
the distance from the center
of
symmetry and
r
the gas index.
Upon identifying
u1
=
p,
'112
=
u,
213
=
p,
there is invariance with
respect
to
the dilatation group provided that
a2=1-7
a3
=
a1
+
2(1-
7)
.
If
the initial density
of
mass
in the medium at rest is:
po(T)
=
ij0r-n
7-r
i-tr
Q=-
(89)
then
a1
=
a
=
-R.
Moreover, if
a
strong explosion takes place at
the origin, then, considering the motion to be self-similar, it follows
from energy conservation
Nonlinear Waves
that
7
is
given by:
3r
-
1
r+i
y=-
.
169
(92)
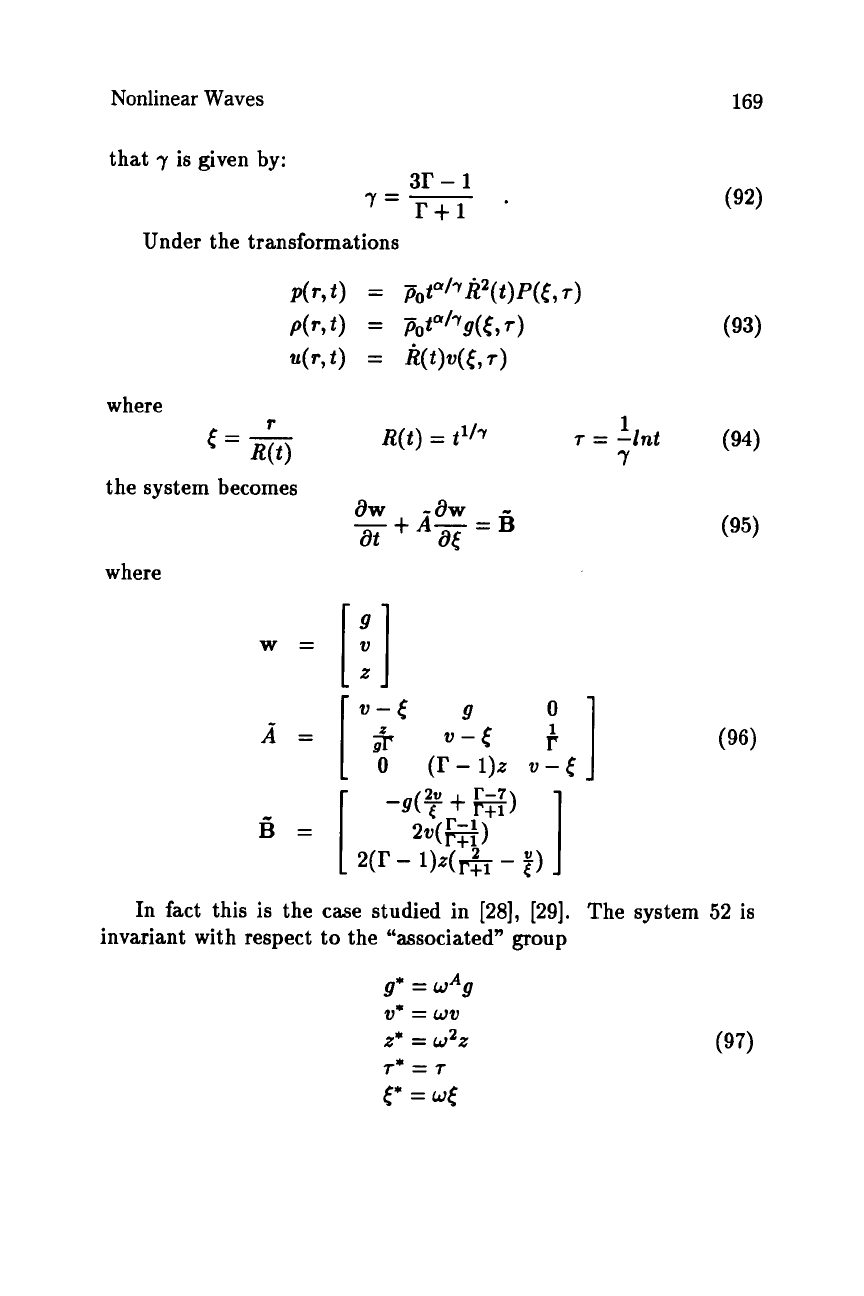
Under the transformations
where
(94)
r
1
t=-
R(t)
=
t'Ir
r
=
-1nt
R(t)
7
the system becomes
at
where
(95)
In fact this
is
the case studied in
[28], [29].
The system
52
is
invariant with respect to the "associated" group
g*
=
wAg
v*
=
wv
z*
=
w2z
r*
=
r
(*
=
wt
(97)
