Ames W.F., Roger C. Nonlinear equations in the applied sciences. Volume 185
Подождите немного. Документ загружается.


130
Shui-Nee Chow and Masahiro Yamashita
To measure the distance between the sections of the stable and unstable manifolds
given in (10.12) and (10.14), we shall 'carry' the section
of
the unstable manifold given
in (10.12) to the hyperplane
r(t2)
+7Z(N2(az))
by the
flow
of
(10.2). Hence, we shall
need the following expressions
of
the unstable and stable manifolds. From (10.8) and
(10.13), we have
E"
=
r(t')
+
"a')[-w'
+
q"
(10.15)
+
Q
L'
O'(t',
s){
N"(B'(s;
t'
,
a';
z'))g(u'(
B'(s;
t'
,
a'
;
2)))
+
(I
-
P)
1;
@(P,
s){
NZ'
(P(
s;
t2
,a2,
2))g(
212
(82(
s;
t2,
a2
;
2)))
(10.16)
=
7(P)
+
eMd(r].).
Now we consider system (10.2) along the heteroclinic orbit
7.
Let
P(t)
and
a(t)
be Cm-bump functions such that
and let
Then system (10.2) becomes
where
B(t)
=
Df(r(t)).
Now let
X(t,s)
be the transition matrix of
y
=
B(t)y
and
let
y(p")(t)
be the solution of (10.17) with the initial condition
y(q")(t')
=
Mu($').
Also define
?(q")
so
that
Y(v")(.2(v"))
E
r(t2)
+
R(Nz(.2)).

Geometry
of
the
Melnikov
Vector
131
We note that
?(q")
=
t2
+
O(lc1)
because of the continuous dependence of solutions
on initial conditions. Therefore
(10.18)
To measure the distance between
y(q")(~~(q"))
and
Ma(q'),
we use linearly in-
dependent bounded solutions on
R
of the adjoint system
i
+
B*(t)4
=
0.
(10.19)
Let
{+I,.
.
.
dm}
be a complete set of linearly independent bounded solutions on
R
of
system (10.19) which satisfy
4i(t2)
E
{R(p)
n
R(N'(~))}~,
i
=
1,.
. .
,
m.
Define

132
Shui-Nee Chow
and
Masahiro Yamashita
By
using
(10.15),
(10.16)
and
(10.18),
Mi
is computed
as
follows.
dT(t2)[Y()?')(T2()?"))
+
+()?V
-
r(t2))1

Geometry
of
the Melnikov Vector
133
Here we let &(t)
=
!I':(t)N'*(#'(t))l
15
t'.
&(t')M'(r]')
=
(b;(tZ)N2(a2)[-w2
+
r]'
Here we let qh(t)
=
\kf(t)iP'(P(t)),
t
2
t*.
Thus we have
(10.20)
and we have proved the following
Theorem
10.1.
The
fist
approximation
of
the Melnikov vector M
=
(6flI..
.
$fm)
for
system
(1
0.2)
is
given by
(10.21)
Mi
=
Lm
4f(t)g(r(t))dtl
i
=
1,.
. .
,
m,
where
rn
is
the number oflinearly independent bounded solutions of
$+[Df(7(t))]'+
=
0.
I
m
Remark
10.2.
Since the heteroclinic orbit
7
is contained both in the unstable man-
ifold
WU(M')
of
M'
and the stable manifold
W'(M2)
of
M2,
it is interesting to
consider how these manifolds intersect each other along the heteroclinic orbit
7.
Con-
sider the case of
a
time-independent perturbation and define

134
Shui-Nee Chow
and
Masahiro Yamashita
where
T7(t)WW(M')
and
T7(,)W'(M2)
are tangent spaces at
y(t)
to
W"(M')
and
W"(M2)
respectively. Then
k
and the dimension
m
of the Melnikov vector have the
following relation.
(10.22)
m
=
n
-
[dim
W"(M')
+
dim
W"(MZ)
-
k],
where
dimW"(M') =dimR(I-Q1)+dl
and
dim
W8(Mz)
=
dimR(P2)
+
dz
.
Note that dim
W"(M')
+
dim
W'(M')
=
n
+
dl
.
If we define the splitting index
6(7)
of
7
by
6(7)
=
dim
W"(M')
-
dim
W8(M2),
we have, from
(12.40)'
the following relation
(10.23)
m
=
k
+
b(7)
-
dl
which is
a
generalization of
(6.2).
Now we go into a special case to which Theorem
10.1
can easily be applied.
Consider a system with a quasi-periodic perturbation
(10.24)
where
g
is periodic in each
't'
argument and
w1,.
. .
,wd
are rationally independent,
see
Meyer and Sell
[13].
We assume that the unperturbed system
i
=
f(z)
has a
homoclinic or heteroclinic orbit
7
to hyperbolic critical point(s). System
(10.24)
is
equivalent to the following system on the torus
Td.
(10.25)

Geometry
of
the Melnikov Vector
135
where
0
=
(@I,.
. .
,
Od),
w
=
(~1,.
. .
,wd)
and
(2,
a)
E
R”
x
Td.
This is
a
special case of
system
(10.2)
in the sense that the ‘2-dynamics’ of the unperturbed system
of
(10.25)
is globally defined in the normal bundle of
Td.
By using the homoclinic orbit
7,
the
homoclinic orbit
7
of system
(10.25)
to
the torus
Td
is given by
‘i.(t)=(Y(t),wl(t),
wlt+&,...,wdt+od)
where
0,
E
[0,27r),
i
=
1,.
. .
,
d.
This is because the ‘2-dynamics’ and ‘&dynamics’ of
the unperturbed system of
(10.25)
are
completely decoupled. By Theorem
10.1,
we
have the following corollary in this
case.
Corollary
10.2.
The first approximation of the Melnikov vector
&f(&,
. . .
,O,)
=
(kl(81,.
.
.
,ed),
. . .
,
&fm(Ol,.
. .
,&))for system
(10.44)
is
given
J-00
i
=
1,.
. .
,
rn.
Here
{+I,.
. .
,
dm}
is
a
set of linearly independent bounded solutions of
i
+
[Df(r(t))l*+
=
0.
As
a
special case, we shall prove the following proposition for two-dimensional
systems.
See
also Meyer and Sell
[13]
and Wiggins
[20].
Proposition
10.3.
Consider system
(10.24)
with the same assumption
as
before
and let
n
=
2
and
d
2
2.
Then the stable and unstable manifolds of system
(10.24)
intersect transversally if and only if for the first approximation of the Melnikov function
k(01,.
. .
,Od)
defined in
(10.26)
(i
=
1
in this case), there exist
(81,.
. .
,8d)
such that
(10.27)
&f(&,
...,&)
=
0
and
(10.28)

136
Shui-Nee Chow
and
Masahiro Yamashita
where
w
=
(w1,.
. .
,wd)
and
CUM
is the Lie derivative
of
M
with respect to
w.
Proof.
Let
&(a)
=
8,
-
w,a,
i
=
1,.
. .
,d,
a
E
R
and define
D(a)
=
M(&(a),
.
. .
,@d(a)).
Then
we
have
and
(10.30)
D(o)=&(81,
...,
8d)=o.
Fkom (10.29)
a
works
as
a
‘sweeping’ parameter along
7.
See Figure
6.
Since
D(a)
changes along
7(a),a
E
R
and since the difference of the true distance
of
the stable
and unstable manifolds and
D(s)
is
of
order
e,
the implicit mapping theorem implies,
using (10.30), that the transversal intersection exists if and only
if
D(0)
=
0
and
D’(0)
#
0.
Finally
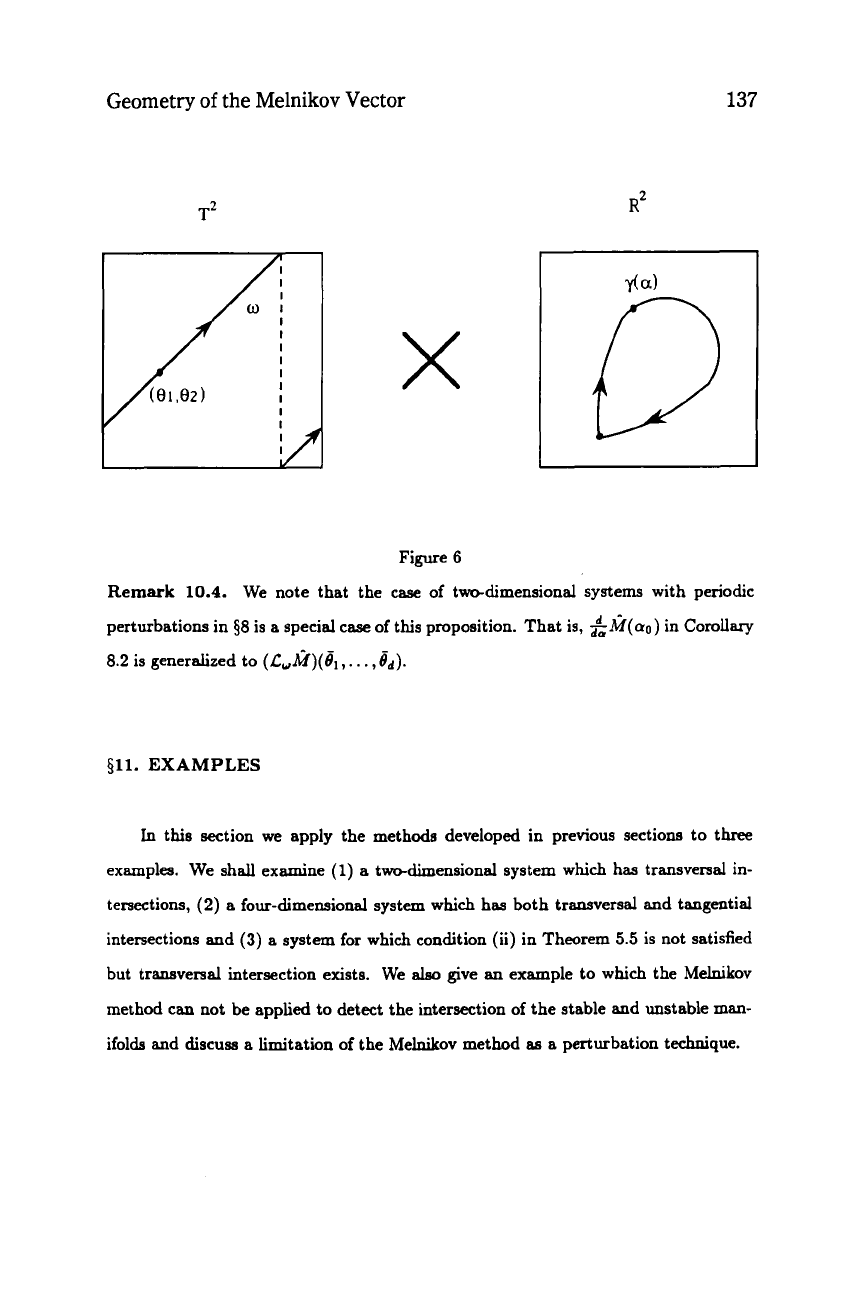
Geometry
of
the Melnikov Vector
T2
137
R'
X
ria)
Figure
6
Remark
10.4.
We note that the case of two-dimensional systems with periodic
perturbations in
58
is
a
special case of this proposition. That is,
f&f(ao)
in
Corollary
8.2
is generalized to
(&,&)(el,.
.
.
,6d).
§11.
EXAMPLES
In
this section we apply the methods developed in previous sections to three
examples. We
shall
examine
(1)
a
two-dimensional system which
has
transversal in-
tersections,
(2)
a
four-dimensional system which has both transversal and tangential
intersections and
(3)
a
system for which condition (ii) in Theorem
5.5
is not satisfied
but transversal intersection exists. We
ale0
give
an
example to which the Melnikov
method can not be applied to detect the intersection of the stable and unstable man-
ifolds and
discusa
a
limitation of the Melnikov method
as
a
perturbation technique.
138
Shui-Nee Chow
and
Masahiro Yamashita
Example
1
(Chow, Hale and Mallet-Paret [4])
We consider the
following
second order equation
3
2
z.
-
2
+
-22
=
€Cost,
(11.1)
where
e
is
sufficiently
small.
That
is,
(11.2)
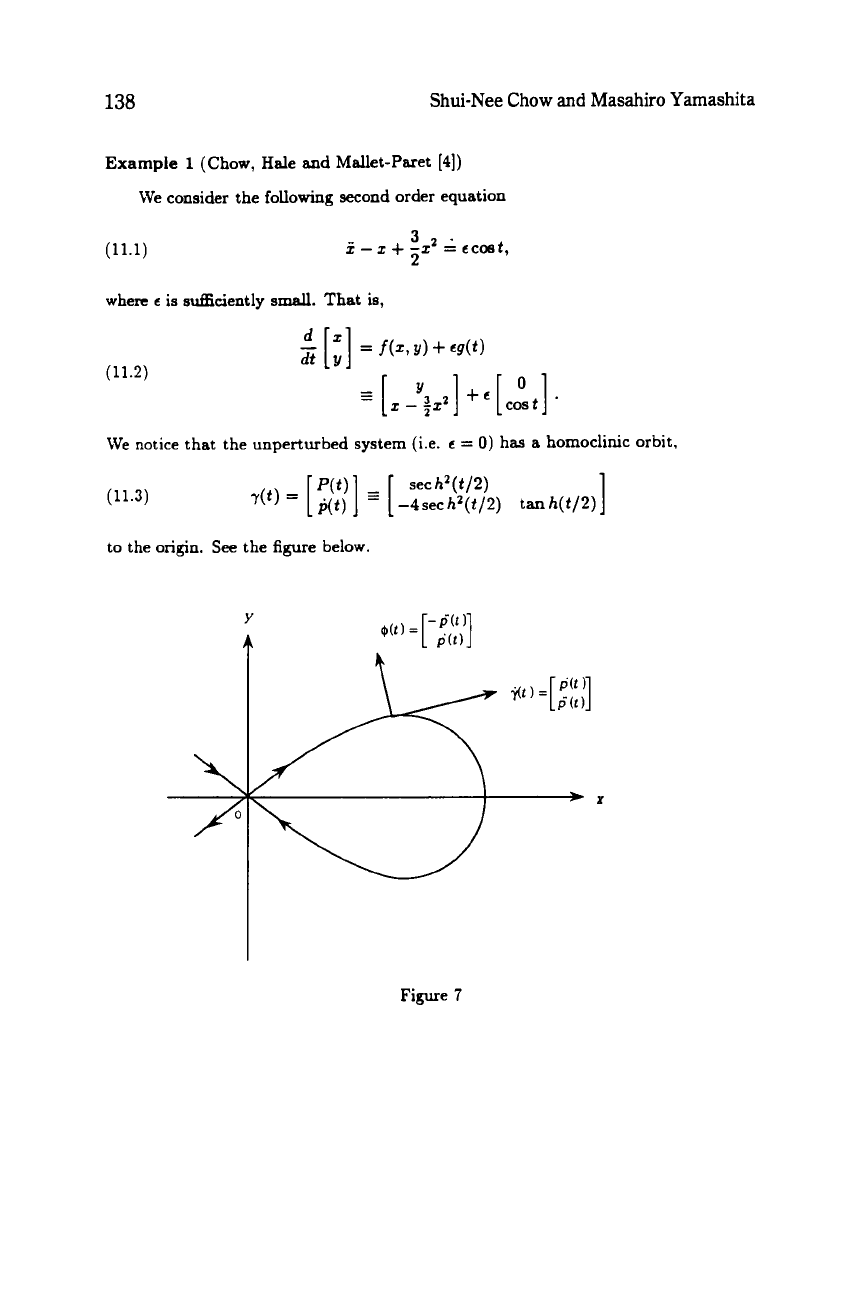
We notice that the unperturbed system (i.e.
e
=
0)
has
a
homoclinic orbit,
(11.3)
-4sec
hz(t/2)
tan
h(t/2)
1
to
the
origin.
See
the figure below.
Figure
7

Geometry
of
the
Melnikov
Vector
139
The linearized system along 7
is
(11.4)
where
(11.5)
i
=
A(t)z
The adjoint system
$+A'(t)#
=
0
has only one linearly independent bounded solution
(11.6)
and hence the first approximation of the Melnikov function is
W
A+)
=
I_,
#*(t)dl
-
W
=
lw
fit)
cos(t
-
a)dt
=
-csina
(11.7)
where
c
>
0
is a constant.
Since
d
da
--n;r(nil)
=
(-l)"+lC,
n
=
O,fl,f2,.
. .
,
(11.8)
the perturbed stable and unstable manifolds always intersect transversally and
so
tangential intersections never occur.
See
Corollary
8.2.
Example
2
(Gruendler
[6])
In this example we consider the following system of two second-order equations.
21
=
I1
-
211(2:
+
2;)
+
€{-3/4121
-
/42&1
1152
coswt},
4/44
(34
+
z;)
coswt
+
-
2/43
+-
1
+wz
1
+wz
(11.9)
22
=
52
-
241:
+
z;)
+
€{--PI
-
12
-
/42&2
+
-
4/43
51x2
coswt
1+wz
+-
2/4r
(5:
+
3z;)coswt}.
1+w2
