Ames W.F., Roger C. Nonlinear equations in the applied sciences. Volume 185
Подождите немного. Документ загружается.


110
Shui-Nee Chow
and
Masahiro Yamashita
where the operator
z(qa)
is
defined
by
To
approximate
z(q")(t),
we use the following iteration scheme:
Set
z!O)(q")(t)
=
0.
Then
Notice that
z(q")(h(t,
Z(q")(g(t
-
a,
r(t),
a,
E))
=
O(
lei)
and hence

Geometry
of
the Melnikov Vector
111
where
q"
E
R(I
-
&(a)),
Iq"I
<<
1
and let
z(q")(t)
be the unique solution of
(4.17).
That is,
z(q")(t)
is the unique solution of
We use the following iteration scheme.
By setting
zp)(p')(t)
=
0,
we have
zY(v")(t)
=
7U(VU)(S(t
-
%7(t)),
z:)(q")(t)
=
zp(p")(t)
+
€zp(p")(t),
and the true solution
z(qU)(t)
satisfies
Notice that, by taking
v
=
qa
=
p"
E
R(P(0))
n
R(I
-
&(a)),z!"(v)(t)
and
zc'(v)
give the first approximation of the Melnikov vector, and
.5i1)(v)(t)
and
Zp)(v)(t)
give
the term of order
c
or higher in the Melnikov vector. Thus we have derived the
following expression
of
the Melnikov vector:
Mi(0,
=
n;r,(a)
+
cd;(a){lR
a(a,t)/t(t,
z;)(v)(t),a,
e)dt
-a
(7.3)
+
/om
@(a,
t)h(t,
z?)(v)(t),
a,
e)dt)
+
O(
14).
In this way we can compute the Melnikov vector in arbitraily high order of accuracy.
It is also clear that it is sufficient to consider the first two terms
in
expression
(7.3)
for the transversality condition in Theorem
5.5.

112
Shui-Nee Chow
and
Masahiro Yamashita
38
THE
FIRST
APPROXIMATION
OF
THE MELNIKOV VECTOR
In
this section we consider some
special
cases
for which the first approximation
of the Melnikov vector gives
suilicient
information for transversal and tangential in-
tersection
of
the stable and unstable manifolds.
We
consider system
(2.1)
and
(2.2)
under the
same
assumption
as
in
52.
Case
(i).
Suppose
where
k
=
dim(R(1-Q(a))nR(P(a))} and
6(y)
is
defined
in
(6.1).
This
means
that
R(P(a))
fl
R(I
-
Q(a))
=
span{j.(a)) and
rn
=
1.
Figure
4
Note
that the Melnikov function in this case is

Geometry
of
the
Melnikov
Vector
113
Proposition
8.1.
Assume
(8.1)
and suppose that there exists
a0
E
IR
such that
U(a0)
=
0
and
-M(aO)
#
0.
(8.3)
da
Then
W&(z-,e)
and
Wic(z+,e)
of system
(2.2)
have
a
point of transversal intersec-
tion.
d-
Proof.
By the implicit function theorem, condition
(8.3)
combining
(8.2)
implies
M(a,e)
=
0
and &M(a,e)
#
0
for some
(Y
near
ao.
Hence this proposition fol-
lows from Theorem
5.5.
8
Note:
Condition
(8.3)
can not be
a
necessary and sufficient condition for transversal
intersection.
Apparently the two-dimensional
case
satisfies condition
(8.1).
In this special
case,
we
have the following corollary.
Corollary
8.2.
Suppose that system
(2.1)
and
(2.2)
are two-dimensional.
Then
W&(z+,
e)
and
Wzc(i-,
e)
of system
(2.2)
have
a
point of transversal intersection if
and only if there exists
a0
E
IR
so
that
(8.4)
da
d-
k(a0)
=
0
and
-M(ao)
#
0.
Proof.
‘If’ part is
a
special case of Proposition
8.1.
Conversely, if transversal inter-
section exists, then by Corolloary
5.8,
there exists
(11
such
that
M(a1,e)
=
0
and
&M(al,e)
#
0.
Using
(8.2),
the conclusion follows from the implicit function theo-
rem.
8
114
Shui-Nee Chow
and
Masahiro Yamashita
Case
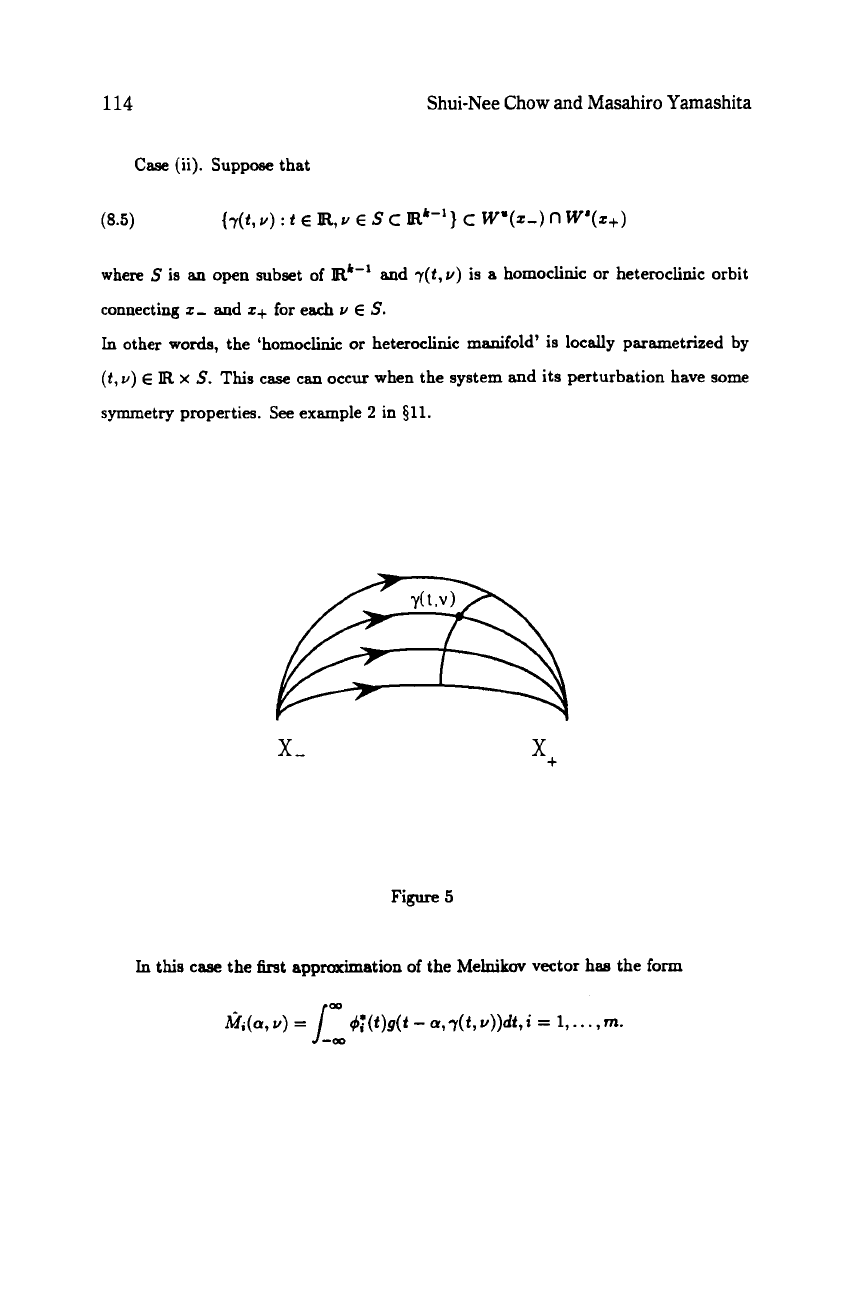
(ii). Suppose that
where
S
is an
open
subset of
ELh-’
and
r(t,v)
is
a
homoclinic or heteroclinic orbit
connecting
z-
and
z+
for each
Y
E
S.
In
other
words,
the ‘homoclinic or heteroclinic manifold’ is locally parametrized by
(t,v)
E
R
x
S.
This case can occur when the system and its perturbation have some
symmetry properties.
See
example
2
in
$11.
X-
i
X
Figure
5
In
this case the
first
approximation
of
the Meluikov vector
has
the form

Geometry
of
the
Melnikov
Vector
Note that
115
M(a,
v,
€)
=
k(a,
v)
+
O(lel).
Hence we have
Proposition
8.3.
Assume
(10.5)
and suppose that there exist
a.
and
vo
such that
(8.6)
n;r(ao,vo)
=
0
and
(8.7)
d
a-
rank[-~(ag,v~)-M(a~,vg)]
=
m.
da
av
Then
Wcc(i-,
e)
and
W;bc(i+,
e)
of system
(2.2)
have
a
point of transversal intersec-
tion.
Proof.
By the implicit mapping theorem, we have
M(al,vl,e)
=
0
and
rank[~;M(al,v~,e)~;M(a~,vl,e)]
=
m
for
(aI,vI)
near
(ao,vo).
Then the state-
ment follows from Theorem
5.5.
I
Remark
8.4.
In the case
m
=
1,
the rank condition
(8.7)
gives
a
necessary and
sufficient condition for transversal intersection.
Next we turn to the tangency condition. Here
a
tangential intersection of the
stable and unstable manifolds means that the tangent spaces
of
the stable and unstable
manifolds at
a
point of intersection do not span the whole space. Our discussion
of tangency is based on Corollary
5.8.
Since Corollary
5.8
gives
a
necessary and
sufficient condition for transversality, we consider the situations in which the condition
in Corollary
5.8
is violated.

116
Shui-Nee Chow
and
Masahiro Yamashita
We consider the following system with parameters.
where
I
E
lR",
E
ElN,
e
<<
1,
f
and
g
are sufficiently smooth in all arguments,
and
g
is periodic in
t.
Assume,
as
before, that the unperturbed system
(e
=
0)
has
a
homoclinic or heteroclinic orbit
~(t).
Recall, first
of
all, that
m
=
k
+
6(7).
Thus it is clear that if
6(7)
>
0,
then
intersection is always tangential
(see
56).
Assume
6(7)
5
0
and assume that
(8.9)
R(P(a))
=
R(I
-
Q((Y))(=
k).
We consider only several special cases here. Extension to more general cases is straight-
forward.
(i) Assume
m
=
1.
This case includes, e.g.,
k
=
1,6(7)
=
0
in
RZ
and
k
=
2,6(7)
=
-1
in
lR3.
We also
assume that
N
2
k.
Proposition
8.5.
Suppose that
(8.10)
(8.11)
and
(8.12)
Then there exists a point of tangential intersection for sufficiently small
c.

Geometry
of
the Melnikov Vector
117
Proof.
Define
Note that
F
:
lFt2kt+1
.--t
Rk+'
and
F(ao,O,po,O)
=
0.
Since conditions (8.10), (8,ll)
and
(8.12) imply that the matrix
has
rank
(k
+
l), by the implicit mapping theorem there exist functions
a(v,e)
and
~(u,
e)
such that
F(44
e),
v9
P(4
€1)
=
0
for sufficiently small
u
and
e.
Hence, the condition in
Corollary
(5.8) is violated
and
the statement follows.
I
See
Wiggins
and
Holmes [21]
for
a
similar result.
(ii) Assume that
m
=
2
and
k
=
2
(and
hence
b(7)
=
0).
Assume
also
that
N
2
3.
Proposition
8.6.
Suppose that
a
(8.13)
fi(a0,Po)
=
&ao,Po)
=
0
and
the matrix
(8.14)
has
rank
4.
Then there exists a point of tangential intersection for sufficiently small
e.

118
Proof.
Define
Shui-Nee
Chow
and
Masahiro Yamashita
a
F(a,
v,
p,
e)
=
(Way
v,p,
&f(%
v,
P.
el).
Then the proof is identical to the one in Proposition 8.5
t
Next we consider
a
more special case.
(ii)’ Assume that
m
=
2,
k
=
2
and
N
2
2,
and assume condition (8.5).
Proposition
8.7.
Suppose that
ah
(8.15)
n;r(ao,vo,cIo)
=
--M(ao,vo,po)
aa
=
0
and the matrix
has rank
4
at
(ao,vo,po).
Then there exists
a
point
of
tangential intersection for sufficiently small
e.
Proof.
Similar to Proposition 8.6.
I
$9
HAMILTONIAN SYSTEMS
In the
case
that the unperturbed system (2.1) is
a
completely integrable Hamilto-
nian system, the Melnikov vector takes particularly simple form even if a perturbation
is non-Hamiltonian.
Assume that
x
=
XH(I),
I
E
nt2”

Geometry
of
the Melnikov Vector
119
is completely integrable, and we consider its non-Hamiltonian and Hamiltonian per-
t urbat ions
and
We shall derive the Melnikov vectors for systems
(9.2)
and
(9.3).
We first recall some basic facts from Hamiltonian systems. Let
H
E
Cw(RZn).
Then the Hamiltonian vector field
XH
with Hamiltonian
H
on
RZ"
is defined by
XH(Z)
=
JVH(2)
Let
Fl,
Fz
E
Coo(Rzn).
The Poisson bracket
(4,
Fz)
of functions
Fl
and
FZ
is defined
bY
{FI,FZ)(z)
=
dFI(Z)XF,(Z),
E
RZn
where dFl is
a
differential 1-form on
R'".
One of the key facts on the Poisson bracket is the following:
{Fl,
Fz)
=
0
if and only if
F,
is
invariant under the flow of
XF~
where
(i,j)
=
(1,2)
or
(2,l).
See
Arnold
111.
We suppose that system
(9.1)
has two hyperbolic critical points
I-
and
Z+
(not
necessarily distinct) joined by
an
orbit
~(t)
of system
(9.1)
:
lim
~(t)=s*.
t-*W
