Ames W.F., Roger C. Nonlinear equations in the applied sciences. Volume 185
Подождите немного. Документ загружается.


90
Shui-Nee Chow
and
Masahiro Yamashita
Remark
3.2.
Notice that
+(a)
E
R(P(a))
n
R(I
-
&(a)).
Since we consider the
cross sections of the time dependent stable and unstable manifolds in a vicinity of the
orbit
y,
it is sufficient, by the tubular neighborhood theorem,
to
consider coordinates
in the normal bundle
u
T$o)R"
of
the submanifold
y,
where
T$.)R"
stands for
the normal vector subspace, in the tangent space
T-,(a)R",
to the one-dimensional
vectorsubspace spanned by
+(a),
i.e.,
T$o,R"
N
T,~,)R"/span{+(a)}. Hence from
now on, we assume, for
7"
E
T-,(,)IR",
qu
E
T-,(,)R"
and
a
E
R,
that
oER
and
qu
E
T$o)R"
n
R(I
-
&(a)).
Remark
3.3.
The 'stable subspace'
R(P(a))
and the 'unstable subspace'
R(1-Q(a))
are uniquely determined. However their complementary subspaces are not uniquely
determined. See Coppel
[5]
for details. Thus we can assume that for each
a
E
R,
Under these assumptions, each point in
Wic(%+,e)
or
Wic(%-,e)
is uniquely ex-
pressed in terms of the coordinates
a,
$
or
7".
Remark
3.4.
The higher order terms
(1
-
P(.))
jOQ(a.
T)h(T,
4V6)(T),
0,
f)dT
and
&(..I
/p,
@(a,
T)h(T,
40U)(T),
a,
W
in
(3.6)
and
(3.8)
are of order
e
uniformly in
a.
Though these terms include the
solutions
z(q')(~)
and
.z(vu)(7)
of equations
(3.3)
and
(3.4),
these solutions can be

Geometry
of
the Melnikov Vector
91
approximated in
an
arbitrarily high order of accuracy by an iterative scheme. In
fact, second iteration is enough to obtain all information we need to determine the
transversality of
W,&(s+,
c)
and
Wic(s-,c).
(See
$7).
$4.
THE FREDHOLM'S ALTERNATIVE
In this section
a
linear version
of
problem
I
in
$2
is considered to develop
a
geometrical idea to solve problem
I
in
52
in general cases. Consider
a
nonhomogeneous
linear system
(4.1)
i
=
A(t)z
+
g(t),
z
E
IR
where
g(t)
is bounded and continuous on
R,
and suppose that the linear system
(4.2)
i
=
A(t)z,
z
E
R"
has exponential dichotomies on
[0,
oo)
with projection
P
and on
(-w,
01
with projec-
tion
Q.
Consider the following
Problem:
Find
a
condition under which system
(4.1)
has
a
bounded solution on
R.
Let
@(t,s)
be the fundamental matrix of system
(4.2).
Then it is known that the
solution
~(t;
0,t")
of
(4.1)
is bounded on
[0,
w)
if and only if
t"
=
77"
+
(I
-
P)
@(O,t)g(t)dt,
(4.3)
J:
and the solution
~(t;
0,
/")
of
(4.1)
is bounded
on
(-00~01
if and only if
(4.4)
t"
=
tl'
+
Q
/O
*(O,t)g(t)dt,
J-m
where
7'
E
R(P)
and
q'
E
R(I
-
Q).

92
Shui-Nee Chow and Masahiro Yamashita
Thus the set of initial data ('(("respectively) which give bounded solutions on
[0,
w)((-w,O])
constitutes the hyperplane which is
a
shift by the constant vector
(I
-
P)
/"
WO,
t)s(t)dt(Q
lo
W,
t)g(t)(dt)
m
--m
of the unperturbed space
R(P)(R(I
-
Q))).
Let
+
iP(O,t)g(t)dt
-
(I
-
P)
@(O,t)g(t)dt.
d=QL
1:
Then we have the following lemma which is the starting point of the paper.
Lemma
4.1.
System
(4.1)
has
a
bounded solution on
R
if
and only
if
(4.5)
+
d
E
R(P)
+
R(1-
Q).
Proof.
This is obvious because condition
(4.5)
is equivalent to say that two hyperplanes
defined by
(4.3)
and
(4.4)
intersect.
I
The geometrical statement in Lemma
4.1
can be expressed analytically by using
bounded solutions of the adjoint system
of
(4.2):
where
A'(t)
is the transpose of
A(t).
Since system
(4.2)
has exponential dichotomies
on
[0,
w)
with projection
P
and on
(-w,O]
with projection
Q,
its adjoint system
(4.6)
automatically has exponential dichotomies on
[0,
w)
with projection
I
-
P'
and on
(-w,O]
with projection
I
-
Q',
where
P'
and
Q'
are adjoint operators of
P
and
Q
respectively.
Notice that
{R(I-
P*)nR(Q*)}
=
{R(P)+R(I-Q)}'
is the subspace of initial
points at
t
=
0
of bounded solutions of the adjoint system
(4.6).
Therefore condition
(4.5)
is equivalent to saying that
d
is annihilated by
4(0)
where
4(t)
is any bounded
solution of the adjoint system
(4.6).
4
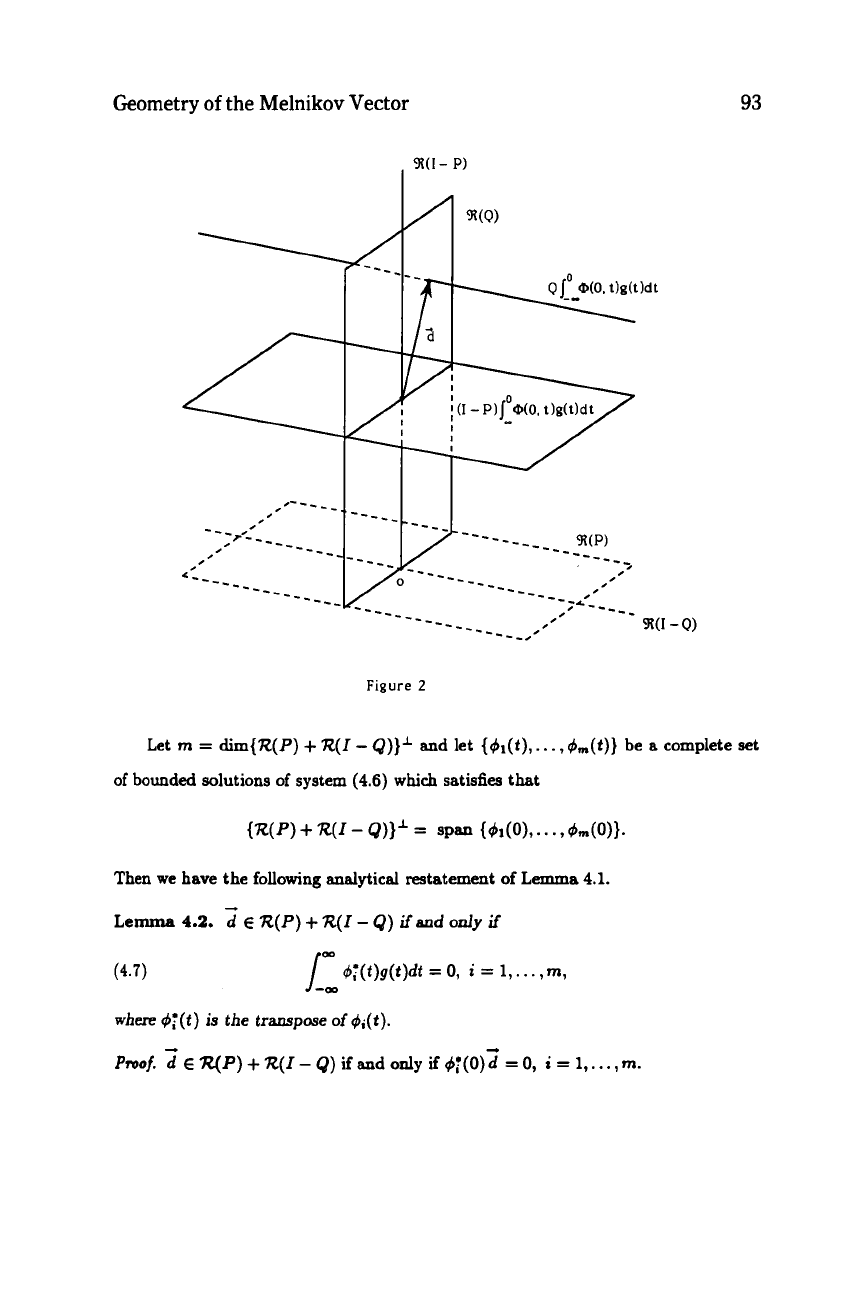
Geometry
of
the Melnikov Vector
93
Figure
2
Let m
=
dim{R(P)
+
R(I-
Q))l
and let
{4l(t),
.
.
.
,
dm(f))
be
a
complete set
of bounded solutions of system
(4.6)
which
satisfies that
Then we have the
following
analytical restatement
of
Lemma
4.1.
Lemma
4.2.
2
E
R(P)
+
R(I
-
Q)
ifand
only
if
(4.7)
W
dT(t)g(t)dt
=
0,
i
=
1,.
.
.
,m,
where
$;(t)
is
the
transpcxse
of
d,(t).
Proof.
2
E
7yP)
+
R(I
-
Q)
if
and
only
if
g;(O)d
=
0,
i
=
1,.
. .
,m.
-

94
Since
and
Shui-Nee Chow
and
Masahiro Yamashita
We remark that Lemma
4.2
had been proved in Chow, Hale and Mallet-Paret
[4] for the two-dimensional
case
and in Palmer [16] for the general case. However
our proof is different and more geometrical. We shall apply in the next section the
method of proof of Lemma 4.2 to the tangent space at each point
of
a
homoclinic
or
heteroclinic orbit.
55.
INTERSECTION OF THE STABLE AND UNSTABLE MANIFOLDS
In this section we will prove our main result that gives computable conditions for
the transversal intersection of the stable and unstable manifolds of system
(2.2)
given
in Proposition
3.1.
To
this end we first derive the Melnikov vector which measures the
'distance' between
Wtoc(Z+,
e)
and
W,'&(s-,
e).
Define, for simplicity, the following
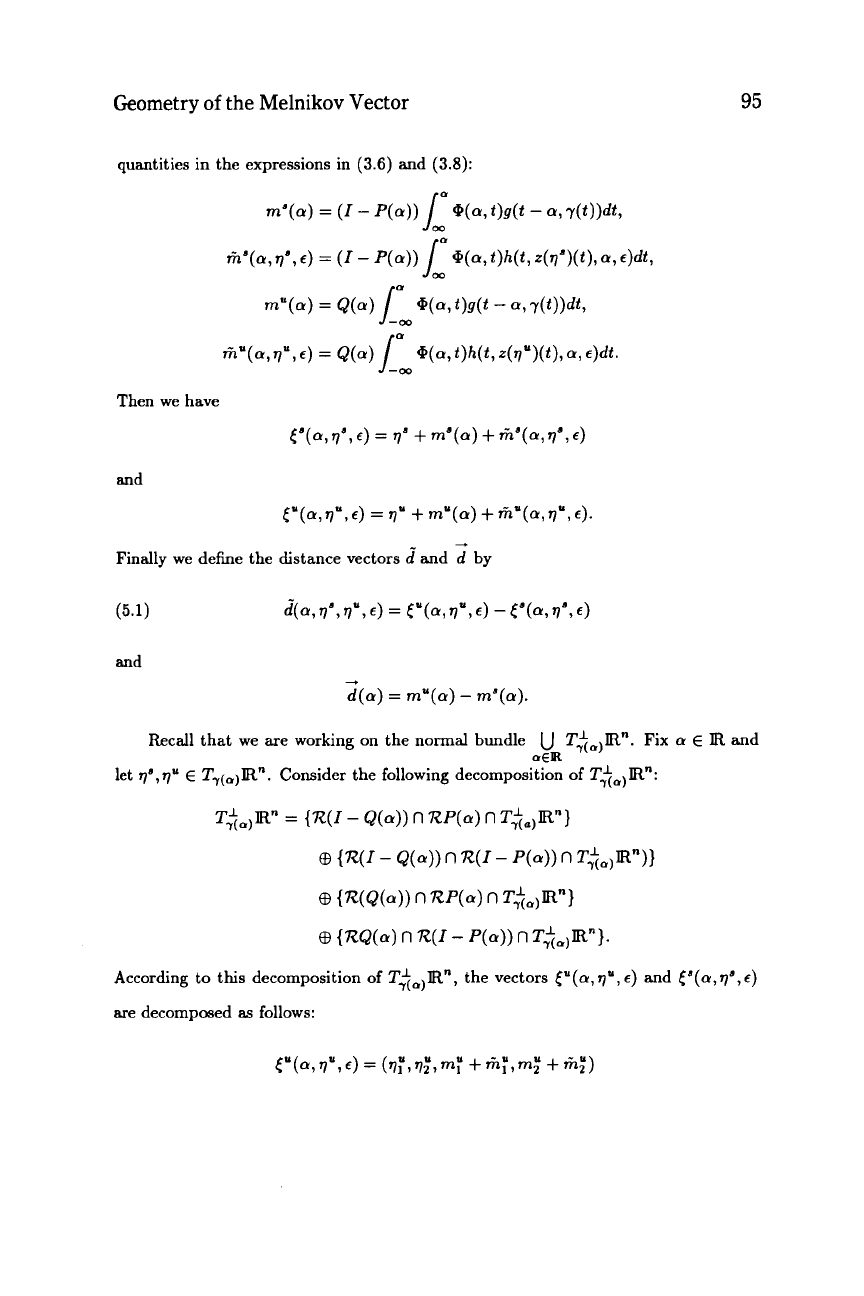
Geometry
of
the
Melnikov Vector
95
quantities in the expressions in
(3.6)
and
(3.8):
Then we have
and
--+
Finally we define the distance vectors
d
and
d
by
and
-
d(a)
=
mya)
-
mya).
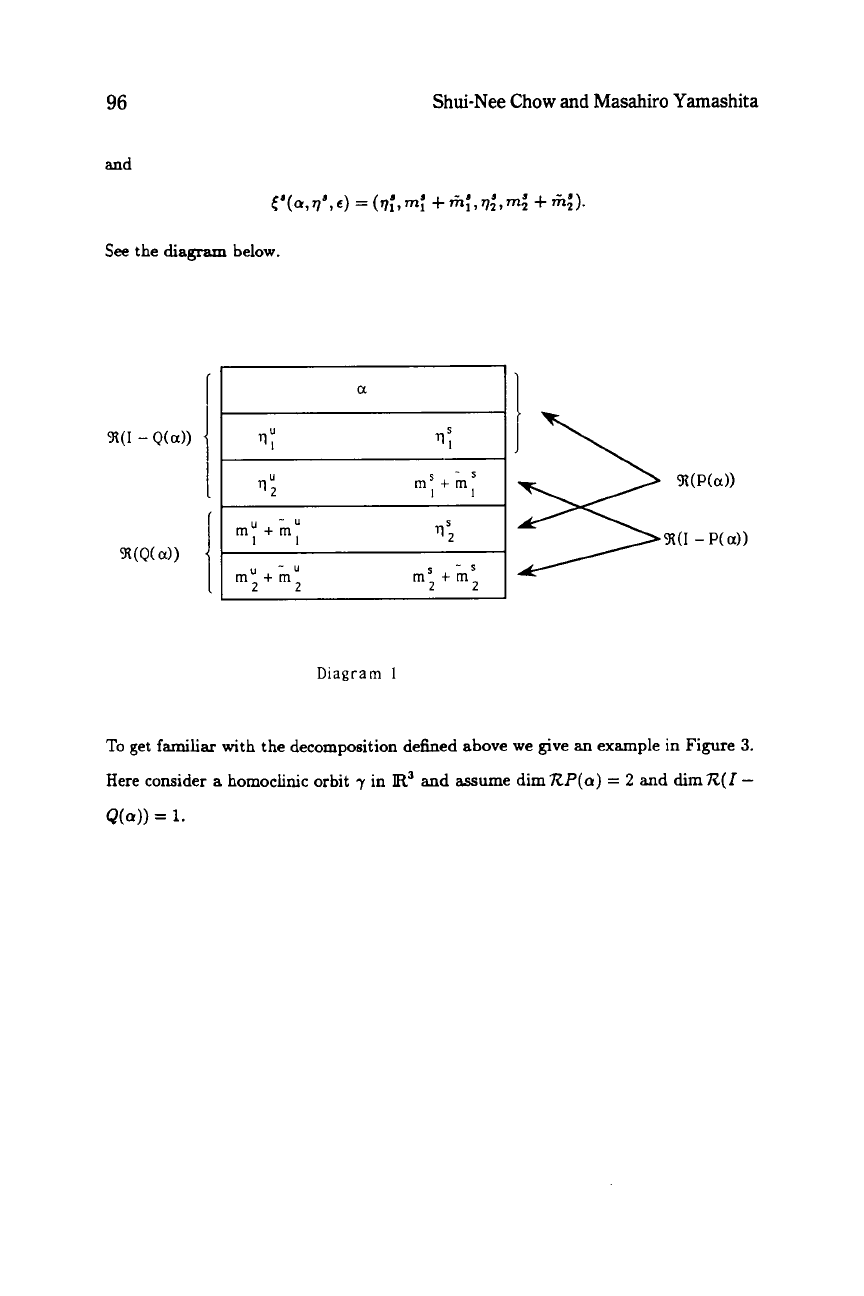
96
and
Shui-Nee
Chow
and
Masahiro Yamashita
%(I
-
Q(a))
I
I
Diagram
1
To get
familiar
with the decomposition defined above we give
an
example in Figure
3.
Here consider
a
homoclinic orbit
7
in
R3
and
assume dimRP(a)
=
2
and dim
R(I
-
Q(0))
=
1.
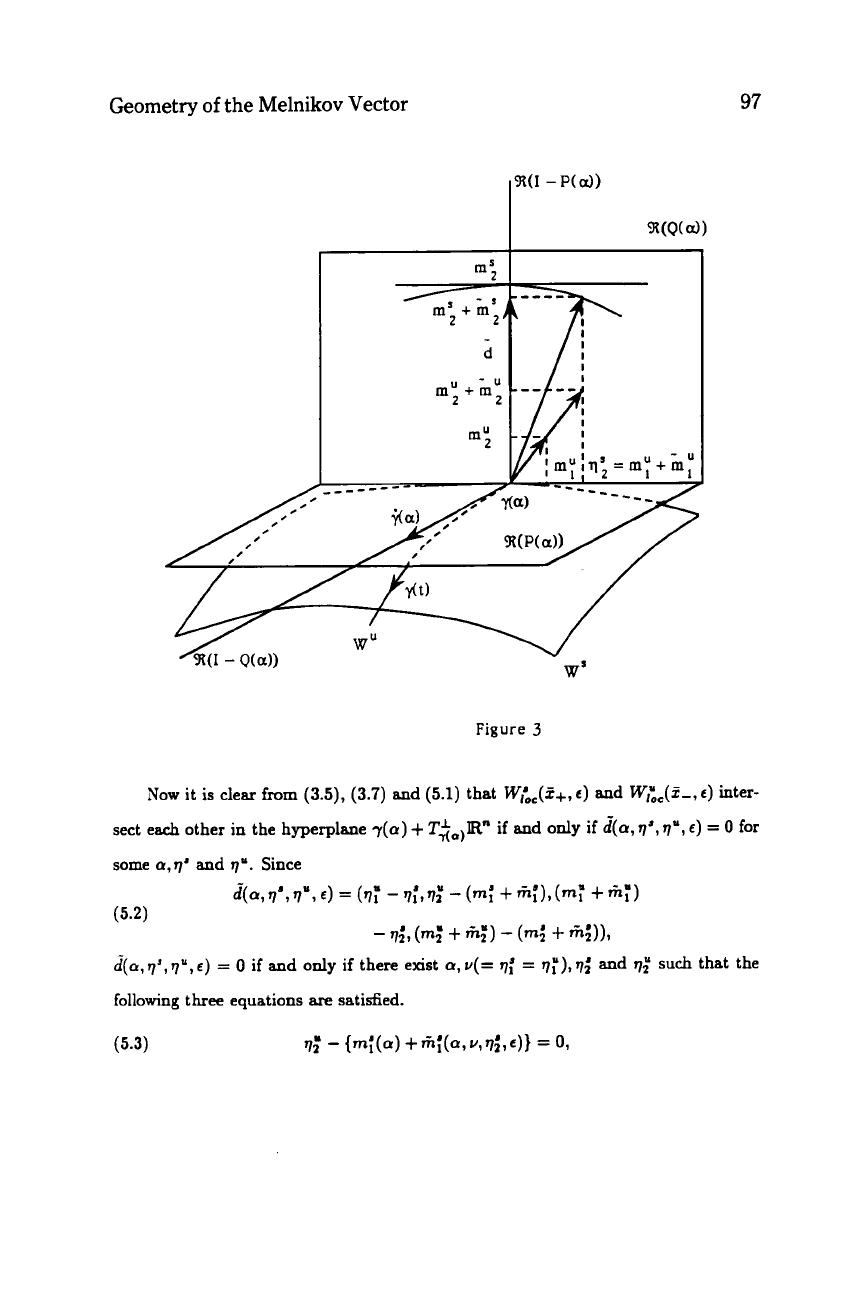
Geometry
of
the
Melnikov
Vector
97
I
rn:
I
W'
Figure
3
Now
it
is
clear
hm
(3.5), (3.7) and
(5.1)
that
W&(Z+,
c)
and
Wcc(5-,
c)
inter-
sect each other in the hyperplane
r(a)
+
T$,,,R"
if and
only
if
(iia,
q',
q",
c)
=
0
for
some
a,q'
and
q".
Since
~(a,q',q",c)
=
0
if
and
only
if there
exist
a,v(=
qi
=
qi'),qi
and
following
three equations
are
satisfied.
such that the

98
Shui-Nee Chow
and
Masahiro Yamashita
From (5.3) and (5.4),
We notice that
is nonsingular for
e
small enough because
Hence, it follows from the implicit mapping theorem that
for
IuI
<<
1.
Similarly, we have
for
1.1
<<
1.
Therefore,
by
(5.5),
J(a,
98,
q',
e)
=
0
if and
only
if
{mX(a)
+
fiX(a,
V,s;(Q,
V,
€1,
(5.8)
-
{mi(a)
+
fi;(a,
v,
s;(a,
v,
e),
e)}
=
0.
To
rewrite (5.8) in
a
more convenient form, we utilize bounded solutions of the
adjoint system
#
+
A*(t)g
=
0
(5.9)

Geometry
of
the Melnikov Vector
99
of
system
(3.2).
Let
(5.10)
rn
=
dim{R(P(a))
+
R(1-
&(a))}*
=
dim(R(1-
P*(a))
n
R(Q*(a))}
and let
{+l(t),
. . .
,
dm(t)}
be
a
complete set
of
bounded solutions of system (5.9) which
satisfies
Then (5.8) is equivalent to the following equations:
.,
-
{m;(a)
+
*;(a,
Y,
$(a,
v,
e), e)}]
=
0,
i
=
1,.
. .
,m,
where
+:(a)
is the transpose
of
+,(a).
Since
&(t)
=
@*(a,t)+,(a),
i
=
1,.
.
.
,mr
and
+:(a)Q(a)
=
+:(a)(1-
P(a))
=
+:(a),
i
=
1,.
. .
,
m,
(5.11) becomes
