Ames W.F., Roger C. Nonlinear equations in the applied sciences. Volume 185
Подождите немного. Документ загружается.


Shui-Nee Chow
and
Masahiro Yamashita
51.
INTRODUCTION
The notion of
a
homoclinic point was introducted by Poincark
[17].
To recall
this concept, consider
a
diffeomorphism in
IRz
with
a
hyperbolic fixed point
p.
A
point
q
is called
a
homoclinic point of
p
if
q
is in the intersection
of
the stable and
unstable manifold of
p.
The point
q
is called
a
transversal homoclinic point of
p
if the
intersection of the stable and unstable manifolds is transversal, i.e. the tangent spaces
at
q
to the stable and unstable manifolds span the whole space. We note that if one
homoclinic point exists, there must be infinitely many homoclinic points.
Poincark already observed that the existence
of
homoclinic points implies com-
plexity
of
the dynamics of the diffemorphism. Later
G.D.
Birkhoff
[3]
proved that
every transversal homoclinic point of
a
a
two-dimensional diffeomorphism is accumu-
lated by periodic orbits. The results by Smale
[19],
now called the Srnale-BirkhoE
theorem, extend the Birkhoff's results both in two dimensional and to higher dimen-
sional
cases
and assert that the existence
of
a
transversal homoclinic point implies the
existence
of
an invariant Cantor set in which the periodic orbits are dense.
See
also
Moser
114).
Moreover, Newhouse
(15)
has proved that there is
a
much more compli-
cated dynamical behavior associated with
a
homoclinic tangency. Thus the dynamics
of diffeomorphisms with transversal
or
tangential homoclinic points
are
fairly well
understood.
However to apply the above abstract theories for diffeomorphisms to
a
system
of
differential equations, we need to know the existence of
a
homoclinic point
of
a
diffeomorphism induced by this system. More precisely, since we shall deal with an
autonomous system with
a
time-period perturbation, the above diffeomorphism ap-
pears
as
a
time-one map, called
a
Poincark map, induced by the flow of the system.
Our
problem is the following: an autonomous system of ordinary differential equa-
tions with
a
time-periodic perturbation is given and we assume that the unperturbed

Geometry
of
the Melnikov Vector
81
autonomous sytem
has
two
hyperbolic critical points (not necessarily distinct) and
a
homoclinic or heteroclinic orbit connecting them. Find computable conditions under
which the Poincark map induced by the perturbed system has
a
transversal home
clinic point. See 52 for more precise definitions of these notions and for
a
rigorous
formulation of the problem.
Poincark [17], Melnikov [12] and Arnold [2] developed such conditions for two-
dimensional analytic Hamiltonian systems and it is now called the Poincark Melnikov
Arnold method
or
simply the Melnikov method. The Melnikov theory has been studied
by several authors, e.g. Chow, Hale and Mallet-Paret
[4],
Holmes [9], and Palmer [16],
and generalizations to higher dimensional cases have also been studied,e.g., Holmes
and Marsden [lo] and Gruendler [6]. The key of these theories is the use of the
Melnikov function which measures the splitting distance between the perturbed stable
and unstable manifolds.
One of the purposes of the present notes is to clarify the geometry of the Melnikov
function (now should be called
the
Melnikov vector) in higher dimensional cases and
to extend the previous theories for the two-dimensional case to higher dimensional
cases.
Our theory is based on the theory of exponential dichotomy. Palmer [16] showed
that the linear variational system along the homoclinic orbit of the unperturbed au-
tonomous system has exponential dichotomies on half-lines. Using this fact we shall
derive explicit expressions of the local stable and unstable manifolds of the perturbed
system in
$3.
Then Fkedholm’s alternative, given in Chow, Hale and Mallet-Paret
[4]
for the two-dimensional case, in Palmer [16] in higher dimensional cases and explained
in
$4,
is used to derive the Melnikov vector in
$5
and we examine conditions for
a
transversal homoclinic point. In $6 we introduce
a
notion of an index of
a
homoclinic
or
heteroclinic orbit which is useful to classify the cases that can occur in higher di-
mensional cases. We discuss
a
relation between the dimension
of
the Melnikov vector

82
Shui-Nee Chow
and
Masahiro Yamashita
and the index
of
the homoclinic or heteroclinic orbit. Numerical aspect of the Mel-
nikov vector is discussed in
97.
In
58
we consider several special cases in which the
Melnikov vectors take simpler
forms,
and
also
we discuss the tangency
of
the stable
and unstable manifolds. We apply these general theories
to
Hamiltonian systems in
$9.
In 510 we extend our theory to the case of
a
heteroclinic orbit to invariant tori and
as
a
by-product we derive
a
formula which guarantees the transversal intersection of
the stable and unstable manifolds
of
a
two-dimensional system with
a
quasi-periodic
perturbation.
See
also Meyer and Sell
[13]
and Wiggins [20]. Several interesting ex-
amples
are
discussed in
$11
and
also
we discuss
a
serious
limitation of the Melnikov
method by using an example for which the Melnikov method does not work.
52.
FORMULATION OF THE PROBLEM
Consider
a
system of differential equations
and its perturbed system
where
seIR",
teIR,
e
E
R
and
lel
<<
1.
The vector fields
f
and
g
are
assumed
to
be
sufficiently smooth and bounded on bounded sets. The vector field
g
is periodic in
t
with the least period
T(>
0).
Assume that system (2.1) has two hyperbolic critical points
I+
and
5-
(not
necessarily distinct). Also assume that there
is
an orbit
7(t),
t
E
R,
of system (2.1)
which connects the critical points
x+
and
x-.
That is,
7(t)
4
I*
as
t
4
foo.

Geometry
of
the
Melnikov
Vector
83
If
z+
=
I-,
the orbit
y
is called
a
homoclinic orbit. Otherwise
y
is called
a
heteroclinic
orbit.
Let
z(t;zo),zo
E
R",
be the solution
of
system
(2.1)
with the initial data
z(0;so)
=
20.
The stable manifold
W'(z+)
of the hyperbolic critical point
I+
of
system
(2.1)
is
defined by
W'(z+)
=
(5oeR"
:
z(t;
Io)
4
I+
as
t
4
+m},
and the unstable manifold
W"(z-)
of the hyperbolic critical point
2-
of the system
(2.1)
is defined by
W"(z-)
=
(I0
E
IR"
:
"(t;
50)
4
5-
as
t
4
-m}.
Then we have
c
w'(z+)
n
W"(Z-)
from the above assumption.
Since the critical points
x*
are
hyperbolic and system
(2.2)
is
periodic in
t,
there
exist unique T-periodic solutions
f*(t;
e)
of system
(2.2)
such
that
lim
f*(t,
e)
=
?*(t,
0)
=
z*
f
-0
uniformly in
t.
For details
see
Hale
(71.
It will be shown in the next section that there exist sets
W&(?+,e)
and
Wcc(?-,c)
in
R"
x
(0)
c
R"
x
R,
where
IR"
x
IR
is the extended phase space
of system
(2.2),
such that
W;b,(f,,e)
=
((50,O)
E
IR"
x
(0)
:
Iz(t;0,20)
-
i*(t;e)I
4
0
as
t
+
+m
and
20
is in
a
sufficiently small neighborhood of
y}
and
W&(f-,€)
=
((z0,O)
E
R"
x
(0)
:
Iz(t;O,q)
-
E(t;e)l
40
as
t
+
-m
and
10
is in
a
sufficiently small neighborhood of
7},

a4
Shui-Nee
Chow
and
Masahiro Yamashita
where
z(t;
T,
zo)
is the solution of system
(2.2)
with
Z(T;
T,
20)
=
10,
zo
E
IR".
If we define the time dependent stable and unstable manifolds,
w(~+;c)
and
w"(Z-,
e),
of system
(2.2)
by
W(Z+,
e)
=
{(zo,
T)
E
IR"
x
IR
:
Iz(t;
7,
zo)
-
Z+(t;
€)I
+
0
as
t
+
+w}
and
W"(Z-,€)
=
((20,T)
E
IR"
x
IR:
lz(t;T,zo)
-
Z-(t;e)l
-+
0
as
t
-+
-a},
then
W&(Z+,e)
and
Wic(Z-,
e)
are the local cross sections at
t
=
0
of
W.(Z+,c)
and
W"(Z-,
c)
respectively. That is,
Since system
(2.2)
is
periodic in
t,
its extended phase space can be regarded
as
R"
x
S',
where
S'
is the unit circle, and
90
W&.(Z+,
c)
and
Wr",,(Z-,
e)
are
the local stable and
unstable manifolds of hyperholic critical points
5&
Z*(O;c)
of the Poincar6 map
II,
:
R"
+
IR",
which
is
defined by the flow of system
(2.2)
aa
follows:
II,(zo)
=
5(T;
O,zo),
50
E
R".
Now we state our problem.
Problem
I.
When does system
(2.2)
have an orbit
z(t),
t
E
IR,
so
that
z(t)
+
Z*(t;
e)
as
t
-+
fw
?
Following the above argument, it is clear that Problem I is equivalent to
Problem
1'.
When do
Wic(5+,e)
and
W&(%-,e),
defined above, intersect each
other?

Geometry
of
the Melnikov Vector
85
Then the next natural question would be
Problem
11.
When do
W&(f++,
e)
and
W&(S+,
c)
intersect transversally?
Here the transversal intersection means that tangent spaces to
Wi,(z+,c)
and to
Wi,(Z-,
e)
at
a
point
of
intersection span the whole space
IR".
$3.
THE STABLE AND UNSTABLE MANIFOLDS
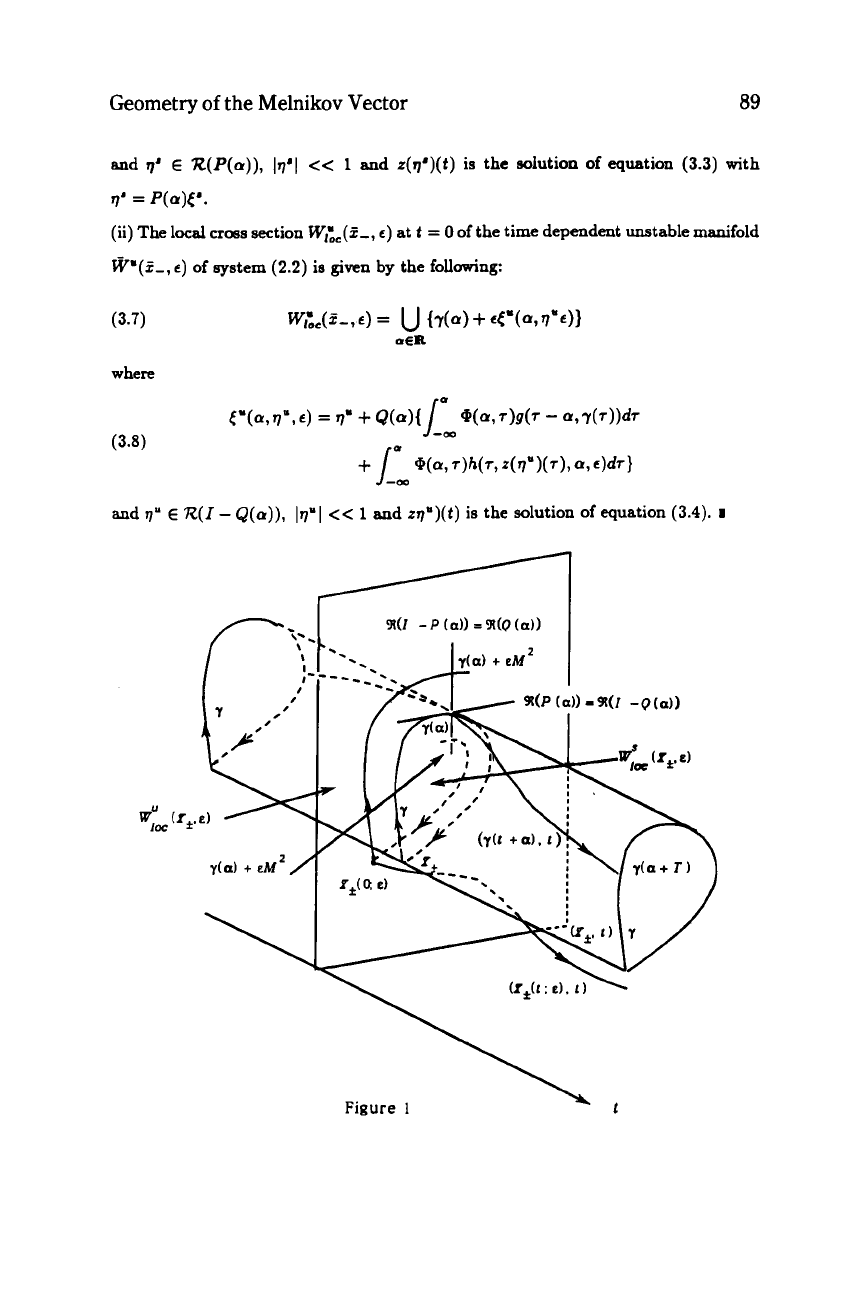
Since we would like to describe the local cross sections
Wroc(Z++,
e)
and
WLc(f-,
c)
of the time dependent stable and unstable manifolds
m'(Z+,e)
and
W"(f-,e)
of
system
(2.2)
aa
parts of the 'perturbed manifolds'
of
W"(z+)
and
W"(z-)
of
system
(2.1)
respectively along the orbit
~(t),
we let, for
a
fixed
a
E
IR,
z(1)
=
T(t
+
a)
+
ez(t
+
a).
Then system
(2.2)
becomes
where
A(t)
=
Df(-y(t))
and
1
h(t,
2%
a,
€1
=
;{f(r(t)
+
4t))
-
f(r(1))
-
eDf(r(t))z(t)
+
'dt
-
a,
r(4
+
4t))
-
edt
-
a,r(t))).
We note that
Ih(t,
z,
a,
€)I
=
O(le1)
uniformly in
t,
z
and
a.
Since
f+(O;
e)
is hyperbolic,
$0)
+
e(
E
Wie(f+,
e)
if
and only
if
the solution
z(t;a,()
of
system
(3.1)
with
z(a;a,()
=
(
is bounded on the time interval
[a,m).
Thus we have, by changing
a
E
R,
that
WAc(f+,
e)
=
u
{y(a)
+
e(*
:
the solution
QER
z(t;
a,
(')
of system
(3.1)
is bounded on
[a,
m)}.

86
Shui-Nee Chow and Masahiro Yamashita
Similarly we have
W&(?-,e)
=
u
{y(a)
+
("
:
the solution
z(t;a,(")
UER
of system
(3.1)
is bounded on
(-00,a]}.
We remark that
a
E
R
works
as
a
'sweeping' parameter along the orbit
y.
See
Figure
1.
Now
as
the orbit
y
is assumed to be a homoclinic or heteroclinic orbit to hyperbolic
fixed points, the linearized system
(3.2)
i
=
A(t)z
of system
(2.1)
along the orbit
y
has
exponential dichotomies on
[a,00)
and
on
(-w,a].
(See
Palmer
(161.)
Recall that system
(3.2)
has
an
exponential dichotomy
on
[a,m)
if
there exists a projection
P(a)
:
R"
-+
IR",
K
2
1
and
a
>
0
such that
and
I@(t,a)(l-
P(a))@(a,s)l
5
Ke-'('-')
,a,
I
t
I
s,
where
@(t,a)
is the transition matrix of system
(3.2).
Similarly system
(3.2)
has an
exponential dichotomy on
(-00,
a]
if there exists
a
projection
&(a)
:
R"
-+
R",
L
2
1
and
b
>
0
such that
and
l@(t,a)(I
-
Q)(a))@(a,s)l
5
Le-b('-L),t
5
s
I
a.
Now
fix
a
6
R.
Then from the variation
of
constants formula, the solution

Geometry
of
the
Melnikov
Vector
87
r(t;
a,
()
of system (3.1) satisfies
where
S(T)
is defined by
S(7)
=
@(T,a)P(a)@(a,T).
It is easy to show that
r(t;
a,
Ed)
is
a bounded solution of system (3.1) on
[a,
m)
if
and only if
~(t;
a,
t8)
satisfies the following integral equation:
z(t;
a,
€8)
=
@(t,
a)P(a)E'
+
@(t,
+
h(7,
z(T;
a,
€9,
a,
€)Id.
J'
@(a,
7)
td'
-
a,
Y(T))
(3.3)
+
@(t,
a)(l-
P(a))
/*
@(a,
7
tS(T
-
a,
T(7))
00
+
h(T,
r(7;
a,
tS),
0,
€)}dT.
Here we used
@(t,T)S(T)
=
@(t,a)P(a)@(a,T).

88
Shui-Nee Chow
and
Masahiro Yamashita
uniformly in
7'.
Similarly
~(t;
a,
t")
is
a
bounded
solution of system
(3.1)
on
(-00,
a]
if and only if
t"
=
7"
+
Q(a){/' *(a,
T)dT
-
a,
r(~)d~
-m
+
1;
@(a,
7)h(T,
Z(rI')(T),
a,
€)dT)
where
q"
E
R(I
-
Q(a)),
the range
of
I
-
&(a),
<<
1
and
z(q")(t)
s
z(t;
a,("($")
is the unique solution of
z(t;
a,(")
=
qt,
a)$
(3.4)
We also remark that
Thus we have shown that
Wic(z+,c)
and
W~,(Z-,c)
have the following expressions
as
functions
of
a,
r]'
or
q".
Proposition
3.1.
(i) The local
cross
section
WLc(Z+,
c)
at
t
=
0
of the time dependent stable manifold
W'"(Z+,e)
of system
(2.2)
is given by the following:
Geometry
of
the Melnikov Vector
89
and
9'
E
'R(P(a)),
19'1
c<
1
and
z(q')(t)
is
the solution
of
equation
(3.3)
with
9'
=
P(a)C'.
(ii)
The local
cross
section Wzc(z-,
c)
at
t
=
0
of the time dependent unstable manifold
w"(f-,
c)
of
system
(2.2)
is
given
by the
following:
(3.7)
