Ames W.F., Roger C. Nonlinear equations in the applied sciences. Volume 185
Подождите немного. Документ загружается.


180
A.
S.
Fokas
Using equation (2.4) to eliminate
k
we find
1
3
3
3i
Pt
=
--pxxx
4
+
VPX
+
WP
+
$P)x
+
;ja;lpyy
+
-p;l(qp)y.
Expressing
v,
w,
q
in terms
of
p(')
(equations (2.4b), (2.6a), (2.7a))
and considering the
00)
of
the above equation we find
Equation (2.8) reduces to the KPI
for
q,
1
3
3
Qt
+
~9xxx
+
2qqx
-
qa;lqyy
=
0.
In
Summary.
The KP
I
equation (2.9) is associated with the
Lax
pair (2.4a) and (2.5). Let
F
be defined by (2.3) and let
p
=
1
+
+
O(&)
be the unique solution
of
(2.1). Then
q
=
-2ipP) solves KPI.
The usual dressing method
for
equations in
1
+
1
yields solutions
which can be thought
of
as perturbations
of
the zero solution. The
starting local
RH
problem is, in general, inadequate
for
capturing
solutions which are perturbations
of
an arbitrary exact solution. It
is interesting that in 2
+
1,
one is able to use the same analytic
structure associated with decaying solutions (namely the non-local
RH
problem (2.1)) to capture bounded but non-decaying solutions.
It seems that this is
a
consequence
of
the decaying in one
of
the two
dimensions. An extended dressing method capturing such solutions
is given in [MI. In particular this method is capable
of
capturing
solutions which are perturbations
of
line-solitons.
(1)
3
A
Cauchy
Problem
for
the
KdV
The KdV equation
Ut
+
~xzz
+
6~~x7
is associated with the Lax Pair

Integrable Nonlinear Equations
181
Ut
=
(Ux
+
v)w
+
(4k2
-
2U)WX,
(3.2)
where
Y
is an arbitrary constant. Indeed, using
(wXx)t
=
(wt),,
and assuming
kt
=
0,
it follows that
u
satisfies the KdV. Because
of
kt
=
0,
equation
(3.1)
is called an isospectral eigenvalue problem.
In order to solve
a
Cauchy problem
for
KdV one needs to analyze
equation
(3.1).
(a)
Analytic Eigenfunctions
The first step of the Inverse Scattering Method is to find appro-
priate solutions of equation
(3.1)
which are analytic in the variable
k.
It turns out that equation
(3.1)
does not have solutions analytic in
the entire complex k-plane. However, it does have solutions analytic
in the upper and lower half-planes. We will denote such solutions
with superscripts
+
and
-
respectively.
As
1x1
+
00,
u
+
0,
thus
w
N
efikX.
Hence there exist
so-
lutions of
(3.1)
which are characterized by the following boundary
conditions:
Since we are looking for analytic solutions it is convenient to get rid
of the exponentials by using
9
=
(b,ikx
=
.,/,e-ikx
(3.4)
Q
=
Je-ikx
Q
=
,$,ikx.
It
turns out that
Q,
Q
are
+
functions, i.e. are analytic in the upper
half complex k-plane, while
6,
\ir
are
-
functions. To establish ana-
lyticity we replace
(3.1)
by appropriate integral equations. Consider
for example
Q:
Since
q5
solves
(3.1),
Q
solves

182
A.
S.
Fobs
aXx
-
2ikaX
=
-u@.
Treating
u@
as
a
forcing, equation
(3.5)
is associated with the Green's
function
G(x,
(,
k,
t),
where
(3.5)
G,,
-
2ikGx
=
-6(x
-
(),
G
+
0
as
x
+
-w.
(3.6)
Equation
(3.6)
yields
G
=
&
-1
+
e2ik(x-c)
0
z
-
[
,
where
0
de-
notes the Heavyside distribution. Hence,
@
solves
(
>(
@(k,x,t)
=
1
+
-
JX
d(
(-1
+
e2ik(x-E))
u([,t)@(k,[,t).
(3.7)
2k
--oo
Equation
(3.7),
for
u&
is
a
Volterra integral equation. Furthermore,
its kernel is
a
+
function with respect to
k;
this follows from the fact
that
x
-
(
is always non negative. Hence its solution
@
is
also
a
+
function. Similarly
Q
solves
Q(k,x,t)
=
1
+
-
d(
(-1
+
e-2ik(x-c))
u([,t)Q(k,[,t).
(3.8)
2;
r
which implies that
Q
is also
a
+
function.
Under the transformation
k
+
-k,
equation
(3.1)
remains in-
variant, while the boundary condition of
!I!
goes to that of
%.
Hence
Q(k,x,t)
=
%(-k,z,t).
Similarly,
q5(k,x,t)
=
&-k,z,t).
Thus
&(k,z,t)
=
@(-k,x,t), %(k,x,t)
=
Q(-k,~,t).
(3.9)
(b)
A
Riemann-Hilbert Problem
Hilbert Problem
[15-171,
i.e. finding
a
relationship between
+
and
-
functions. Using the linear independence property of the solutions of
the second order ODE
(3.1),
we obtain
q5
=
alZ)
+
b$.
This equation
together with
(3.4), (3.9)
implies
The second step of inverse scattering involves formulating
a
Riemann-

Integrable Nonlinear Equations
183
The functions
a,
b
are constant with respect to
2,
and can be inter-
preted as the transmission and reflection coefficients. The functions
@
and
Q
and
-t
functions, hence
Q(-k,x,t)
is
a
-
function. What
about
a,
b?
It turns out that
b
has no analytic properties in
k
but
1/a
is
a
+
function. This follows from the following expressions for
a,
b:
To
derive these expressions let
A
=
@(k,a:,t)
-
a(k,t)q(-k,x,t).
Then equations
(3.8), (3.9)
imply that
A
satisfies
On the other hand, using
(3.10),
A
=
(using
(3.9)),
and hence it satisfies
Comparing the two equations for
A,
equations
(3.11)
follow.
It can be shown
[19]
that a(k,
t)
may have simple zeros
kl,
. .
,
kN
in the upper half k-complex plane. Hence in general
@/a
will be
meromorphic in the upper half k-plane.
So
let
(3.12)

184
A.
S.
Fokas
where
@+
is
a
+
function.
Equations
(3.12), (3.10)
suggest that
Aj
=
cj(t)e2ikjzQ(kj,z7t).
This can be verified by using an argu-
ment similar to the one used to derive
(3.11).
Thus equation
(3.10)
becomes
(3.13)
Equation
(3.13)
defines
a
Ftiemann-Hilbert problem: Given
cj, kj,
p,
find
@+,
Q.
Applying
a
-
projection of
(3.13),
and letting
k
--t
-k
we find
(3.14)
Equation
(3.14)
and the equations obtained by evaluating
(3.14)
at
k
=
kj,
define
a
system of linear integral equations for
Q.
Since
u
can be found in terms of
Q
from equation
(3.1),
u
also can be
expressed in terms of the scattering data. Rather than using
(3.1),
the following expression is more convenient,
Equation
(3.14)
expresses
Q
in terms of the
scattering data
cj,
kj,
p.
Let us summarize: Given the scattering data
{cj(t),
kj}gl, p(k,t),
equation
(3.14)
yields
Q
and then equation
(3.15)
implies
u.
This
scheme will be useful for solving
a
Cauchy problem for KdV provided
that one can determine the scattering data from knowledge of
u(x,
0).
This is indeed the case, and is
a
consequence of the fact that
cj,
p
have
a
simple time evolution (recall that
kit
=
0):
(3.16)
8ik3t
cj(t>
=
cj(0)esik?
7
P(k4
=
p(k70)e
*

Integrable Nonlinear Equations 185
To obtain the evolution
of
p
note that since
4
N
e-ikx
as
2
-+
-ca
equation (3.2) yields
u
=
4ik3. Also
Cp
N
ae-jkZ
+
beikx as
z
-+
00;
substituting this expression into (3.2) with
v
=
4ik3, it follows that
at
=
0,
bt
=
8ik3b.
The evolution
of
cj(t)
is obtained in
a
similar way.
In summary: The initial data
u(z,
0)
implies kj,cj(O),p(k,
0).
Then equations (3.16) yield the scattering data for arbitrary
t,
which
in turn (through
Q)
imply
u(z,t).
Remarks
1.
Pure soliton solutions correspond to
p
=
0.
Hence they are
characterized through the linear system of algebraic equations
j=1
(3.17)
2. To establish the correction with the direct linearization note
that (3.14) can be written as
where
P(4
O)dJ
for
1
real
-2ricj(O)&(l-
kj)dl for
1
imaginary.
dW)
=
3.
In
the original formalism
of
inverse scattering the basic linear
integral equation was not equation (3.14) but the Gel'fand-
Levitan-Marchenko equation.
To
derive this equation assume
that

186
A.
S.
Fokas
00
q(l~,
2,
t)
=
1
+
J,
ds~(s,
s,
t)eik(s-z).
(3.19)
Substituting
(3.19)
in
(3.18)
and operating with
&
JR
dlceik(("-Y)
one obtains
where
Also equation
(3.15)
now becomes
u(2,
t)
=
2azIi(2,
2,
t).
(3.22)
4.
Perhaps the most important consequence
of
the inverse scat-
tering method is that it allows one to evaluate the long time
behavior
of
u(2,t).
As
t
+.
00,
stationary phase analysis im-
plies that only the part
of
(3.14)
associated with the discrete
spectrum survives (the continuous spectrum gives
a
contribu-
tion which decays like
l).
Hence equations
(3.14), (3.15)
for
large
t
reduce to equations
(3.17).
Thus any initial data will
decompose into
a
number
of
solitons as
t
--f
00.
This
is
in my
opinion why solitons are
so
important: They describe the long
time behavior
of
the nonlinear equation under consideration.
4
4
A
Cauchy Problem
for
N-Wave Interac-
tions in
2
+
1.
The N-wave interaction equation in
2
+
1,

Integrable Nonlinear Equations
187
c;-c,
where
a;j
+
J.
Jz,i
#
j
and
C;,
Ji
are arbitrary real constants is
associated with the following linear eigenvalue problem
1-
J
aP
aP
ax
ay
-
-
J-
=
ikjp
+
Qp,
jA
=
[J,A].
In equation
(4.2):
(i)
p
is an
N
x
N
matrix-valued function on
W2(N
2
2),
(ii)
J
is
a
constant, real diagonal
N
x
N
matrix with en-
tries
J1
>
Jz
>
.
-
-
>
JN
and
Q
is off-diagonal with rapidly decaying
component functions.
Actually, equation
(4.2)
is also the time-independent part of the
Lax pair of the Davey-Stewartson
I
(DS) equation and modified
KPI
equation. Equation
(4.1)
has been considered in
[20].
Here we follow
Writing equation
(4.2)
in component
form
we find
Let
fub([,
qa)
:=
jab([,
qa
-
Ja[),
then equation
(4.3)
becomes
(j&b)E
-
ik(Ja
-
Jb)pab
=
(&lab,
which can be converted into the integral equation
where
Crab
are arbitrary constants and
(Lab
are arbitrary functions of
(qa,
k).
Writing this equation in the original coordinates we obtain
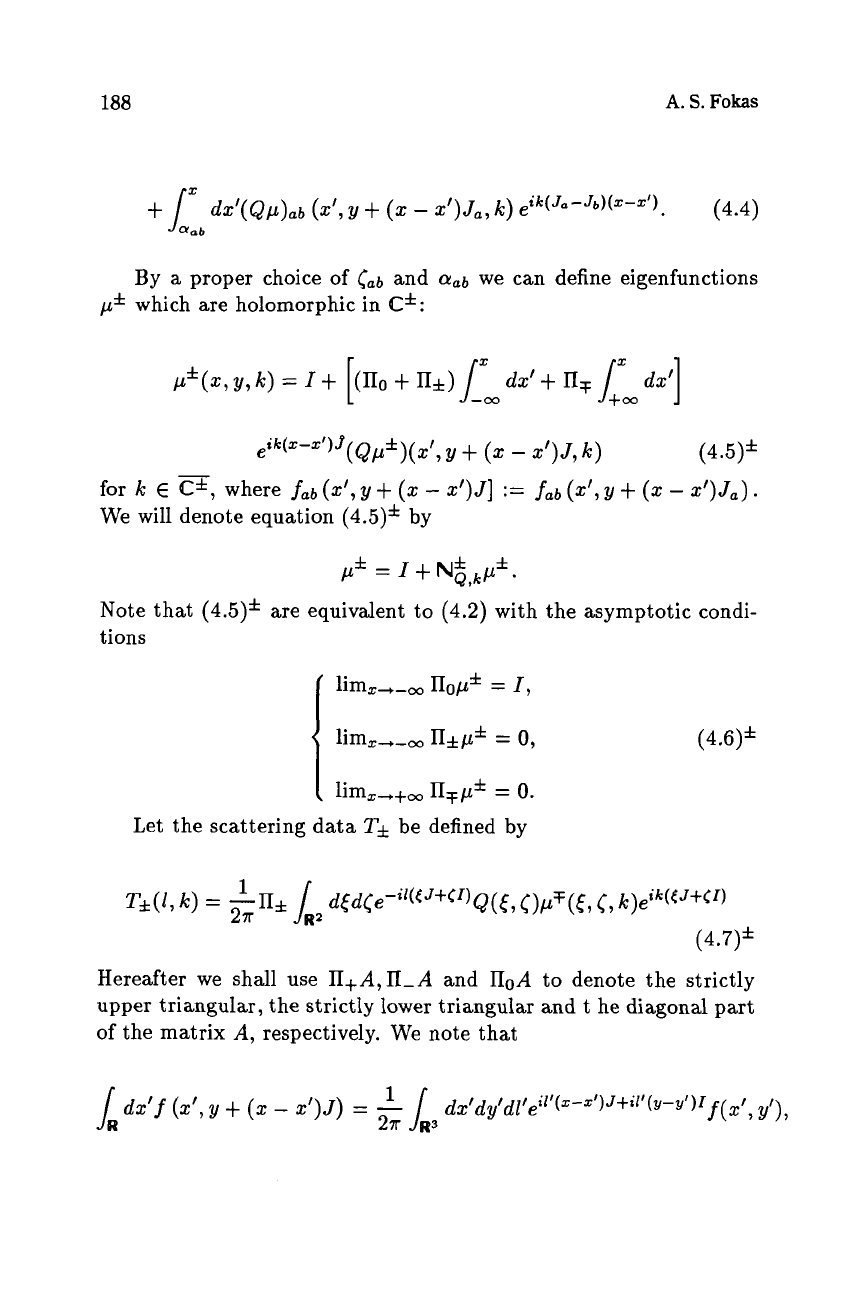
188
A.
S.
Fokas
By
a
proper choice of
cab
and
(Y,b
we can define eigenfunctions
p*
which are holomorphic in
C*:
eik(”-”’)’(Qp*)(z’,
y
+
(z
-
z’)J,
Ic)
(4.5)f
for
IC
E
S,
where
fab
(z’,
y
+
(z
-
z‘)~]
:=
jab
(z‘,
y
+
(z
-
3’)~~).
We will denote equation
(4.5)*
by
/Lf
=
I
+
N;,kLL*.
Note that
(4.5)*
are equivalent to
(4.2)
with the asymptotic condi-
tions
I
Iimz-,+OO
n,pf
=
0.
Let the scattering data
Tf
be defined by
ik(
E
J+CZ)
1
w,
k)
=
Z;;h
JR2
dtdce-i[(CJ+Cz)Q(t,
0PF(t,
c,
we
(4.7)f
Hereafter we shall use
II+A,lLA
and
IIoA
to denote the strictly
upper triangular, the strictly lower triangular and
t
he diagonal part
of the matrix
A,
respectively. We note that

Integrable Nonlinear Equations
189
thus equation
(4.5)*
becomes
Letting
1’
+
k
=
1
in these equations and taking
x
+
-co
we obtain
lim
(p*(x,
y,
k)
-
I)
eik(lJ+Yz)
=
-
J.
dZe”‘TF(l,
k).
(4.8)*
24--00
Throughout this paper the large
x
limit
of
the
ab
component is taken
along the characteristic line
y
+
xJa
=
va,
where
71,
-
- -
,
7~
are the
compartments
of
the diagonal matrix
7.
The eigenfunction
po
is defined by
X
(Qpo)
(x’,
y
+
(5
-
x’)J,
k)
,
k
E
R.
dx/eik(z-z’)3
P0(X7
Y,
4
=
I
+
1,
(4.9)
We will denote equation
(4.9)
by
/lo
=
I
+
N$,kpo.
Note that
(4.9)
is equivalent to
(4.2)
with the asymptotic condition
0
lim
p
=
I.
z+-m
(4.10)
Using the asymptotics
of
p*
and
po
as
x
t
-co
it is straightfor-
ward to relate these eigenfunctions:
