Amano R.S., Sunden B. (Eds.) Computational Fluid Dynamics and Heat Transfer: Emerging Topics

Подождите немного. Документ загружается.

Sunden CH008.tex 10/9/2010 15: 19 Page 326

326 Computational Fluid Dynamics and Heat Transfer

(a)

y/δ y/δ

DNS

NLHN

Present

−6

 15

 10

 7.5

 2.5

 1.0

uθ

(b)

012

DNS

NLHN

Present

= 15

= 10

= 7.5

= 2.5

= 1.0

υθ

Figure 8.47. Predicted turbulent heat ﬂux (Case 2); (a) streamwise (uθ), (b) wall-

normal (

vθ).

−1

−5

−7

−1

−3

= 2.5

DNS

NLHN

Present

uθ

υθ

uθ

Figure 8.48. Wall-limiting behavior of turbulent heat ﬂuxes (Case 2).

turbulent heat ﬂux,

wθ, is expressed by the present model in Case 2 as follows:

wθ =−



∗

θ1







∂

∂y

(81)

θ1



(

θ2

+ C

θ3

)

∂

∂y

+ 2C

θ1





∂

∂y

Thewall-limitingbehaviorsofturbulent heatﬂuxesareshowninFigure8.48,in

which the wall-limiting behaviors are properly satisﬁed by the present NLEDHM.

Sunden CH008.tex 10/9/2010 15: 19 Page 327

Recent developments in DNS 327

On thebasis of theseevidences, itwouldnot be anoverstatement tosaythat the

proposed model can be applied to predict the rotating heated channel ﬂows with

arbitrary rotating axes.

8.10 Concluding Remarks

Based on our current works, the recent trends in DNS and turbulence models for

velocity and thermal ﬁelds have been over viewed in this chapter. Without dispute,

the DNS gives us a possibility to obtain highly accurate information on various

turbulence quantities.Within the foreseeable future, DNS researchers will actively

tackle more complex problems, e.g., ﬂows at high Reynolds or Prandtl numbers,

buoyancy-drivencomplexﬂows,and atmosphericboundarylayer ﬂows.Of course,

itis true thatthe power ofthe presentsupercomputer systemdoes notofferrealistic

solutions to the above problems. However, improvement of computer systems, in

particular, the further development of massive parallel-computing systems will

conquer most of the serious difﬁculties which confront us now. In fact, there are

emergingindustrieswhichaimforpetaﬂops(PFLOPS)computing.Newresearches

concerning exascale supercomputing design are also in progress.

The latest turbulence models for velocity and thermal ﬁelds deal with the indi-

vidualelementalprocessesofturbulence withthe aidof detailedinformationgiven

by DNS. As a result, such models can mimic the DNS with high accuracy. Also,

manyattempts toconstruct auniversalturbulence modelare being made. Ifa num-

ber of DNS databases on complex turbulent ﬂows are constructed in the future, we

will be able to approach the universal turbulence model.

Acknowledgment

This study was partially supported by a Grant-in-Aid for Scientiﬁc Research (S),

17106003, from the Japan Society for the Promotion of Science (JSPS).

References

[1] Robinson, S. K. Coherent motions in the turbulent boundary layer, Annu. Rev. Fluid

Mech., 23, pp. 601–639, 1991.

[2] Kasagi, N. Direct numerical simulation data bases: an effective tool in fundamental

studies ofturbulent heat transfer, Computers and Computing in HeatTransfer Science

and Engineering, W. Nakayama and K.T.Yang, eds., CRC Press, Florida, pp. 97–117,

1993.

[3] Mansour, N. N., Kim, J., and Moin, P. Reynolds-stress and dissipation-rate budgets in

a turbulent channel ﬂow, J. Fluid Mech., 194, pp. 15–44, 1988.

[4] Nagano, Y., and Shimada, M. Critical assessment and reconstruction of dissipation-

rate equations using direct simulations, The Recent Developments in Turbulence

Research,Z.S.ZhangandY.Miyake, eds.,InternationalAcademicPublishers,Beijing,

pp. 189–217, 1994.

Sunden CH008.tex 10/9/2010 15: 19 Page 328

328 Computational Fluid Dynamics and Heat Transfer

[5] Rogers, M. M., Mansour, N. N., and Reynolds, W. C. An algebraic model for the

turbulent ﬂux of a passive scalar, J. Fluid Mech., 203, pp. 77–101, 1989.

[6] Kim, J., Moin, P., and Moser, R.Turbulence statistics in fully developed channel ﬂow

at low Reynolds number, J. Fluid Mech., 177, pp. 133–166, 1987.

[7] Moser, R. D., Kim, J., and Mansour, N. N. Direct numerical simulation of turbulent

channel ﬂow up to Re

=590, Phys. Fluids, 11, pp. 943–945, 1999.

[8] Spalart, P. R. Direct simulation of a turbulent boundary layer up to R

=1410, J. Fluid

Mech., 187, pp. 61–98, 1988.

[9] Spalart P. R., and Watmuff, J. H. Experimental and numerical study of a turbulent

boundary layer with pressure gradients, J. Fluid Mech., 249, pp. 337–371, 1993.

[10] Le,J.-H.,andSung,H.J.Effectsofanadversepressureg radientonaturbulentboundary

layer, Int. J. Heat Fluid Flow, 29, pp. 568–578, 2008.

[11] Le, H., Moin, P., and Kim, J. Direct numerical simulation of turbulent ﬂow over a

backward-facing step, J. Fluid Mech., 330, pp. 349–374, 1997.

[12] Choi, H., Moin, P., and Kim, J. Direct numerical simulation of turbulent ﬂow over

riblets, J. Fluid Mech., 255, pp. 503–539, 1993.

[13] Nagano,Y., Hattori, H., and Houra,T. DNS of velocity and thermal ﬁelds in turbulent

channel ﬂow with transverse-rib roughness, Int. J. Heat Fluid Flow, 25, pp. 393–403,

2004.

[14] Kristoffersen, R., and Andersson, H. I. Direct simulations of low-reynolds-number

turbulent ﬂow in a rotating channel, J. Fluid Mech., 256, pp. 163–195, 1993.

[15] Oberlack, M., Cabot, W., and Rogers, M. M.Turbulent channel ﬂow with streamwise

rotation: lie group analysis, DNS and modeling, Proc. 1st Int. Symp. on Turbulence

and Shear Flow Phenomena, pp. 85–90, 1999.

[16] Nagano,Y.,andHattori,H.DNSandmodellingofspanwiserotatingchannelﬂowwith

heat transfer, J.Turbulence, 4-010, pp. 1–15, 2003.

[17] Wu, H., and Kasagi, N. Effects of arbitrary directional system rotation on turbulent

channel ﬂow, Phys. Fluids, 16, pp. 979–990, 2004.

[18] Hattori, H., Ohiwa, N., and Nagano, Y., Nonlinear eddy diffusivity model for wall-

bounded ﬂow with arbitrary rotating axes, Int. J. Heat Fluid Flow, 27, pp. 838–851,

2006.

[19] Huser, A., and Biringen, S. Direct numerical simulation of turbulent ﬂow in a square

duct, J. Fluid Mech., 257, pp. 65–95, 1993.

[20] Sumitani, Y., and Kasagi, N. Direct numerical simulationof turbulent transport with

uniform wall injection and suction,AIAA J., 33, pp. 1220–1228, 1995.

[21] Iida, O., and Kasagi, N. Direct numerical simulation of unstably stratiﬁed turbulent

channel ﬂow,Trans. ASME, J. Heat Transfer, 119, pp. 53–61, 1997.

[22] Hattori, H., and Nagano, Y. Direct numerical simulation of turbulent heat transfer in

plane impinging jet, Int. J. Heat Fluid Flow, 25, pp. 749–758, 2004.

[23] Hattori, H., Houra, T., and Nagano, Y. Direct numerical simulation of stable and

unstable turbulent thermal boundary layers, J. Heat Fluid Flow, 28, pp. 1262–1271,

2007.

[24] Hattori, H., Morita, A., and Nagano, Y. Nonlinear eddy diffusivity models reﬂecting

buoyancy effect for wall shear ﬂows and heat transfer, Int. J. Heat Fluid Flow, 27, pp.

671–683, 2006.

[25] Speziale,C.G.,Sarkar,S.,andGatski,T.B.Modellingthepressure-straincorrelationof

turbulence: an invariant dynamics systemapproach,J. Fluid Mech.,227, pp. 245–272,

1997.

Sunden CH008.tex 10/9/2010 15: 19 Page 329

Recent developments in DNS 329

[26] Kajishima, T. Finite-difference method for convective terms using non-uniform grid,

Trans. JSME (B), 65, pp. 1607–1612, 1999.

[27] Perry,A.E.,Schoﬁeld,W. H., andJoubert, P. N.Roughwall turbulent boundarylayers,

J. Fluid Mech., 37, pp. 383–413, 1969.

[28] Townsend, A. A. The Structure of Turbulent Shear Flow, 2nd Edition, Cambridge

University Press, Cambridge, pp. 139–143, 1976.

[29] Hanjali´c, K., and Launder, B. E. Fully developed asymmetric ﬂow in a plane channel,

J. Fluid Mech., 51, pp. 301–335, 1972.

[30] Kasagi, N., and Nishimura, M. Direct Numerical simulation of combined forced and

natural turbulent convection in a vertical plane channel, Int. J. Heat Fluid Flow, 18,

pp. 88–99, 1997.

[31] Kays, W. M., and Crawford, M. E. Convective Heat and Mass Transf., 3rd Edition,

McGraw-Hill, NewYork, pp. 323–325, 1993.

[32] Dean, R.B.Reynoldsnumberdependenceofskinfrictionandotherbulkﬂowvariables

in two-dimensional rectangular duct ﬂow, Trans. ASME, J. Fluid Engng., 100, pp.

215–223, 1978.

[33] Ashraﬁan,A., andAndersson, H.I.DNSofturbulentﬂowin a rod-roughened channel,

Proc. 3rdInt. Symp. onTurbulence andShearFlowPhenomena, 1, pp. 117–122,2003.

[34] Leonardi, S., Orlandi, P., Smalley, R. J., Djenidi, L., andAntonia, R.A. Direct numer-

ical simulations of turbulent channel ﬂow with transverse square bars on one wall, J.

Fluid Mech., 491, pp. 229–238, 2003.

[35] Vogel, J. C., and Eaton, J. K. Combined heat transferand ﬂuid dynamic measurements

downstream of a backward-facing step, Trans. ASME, J. Heat Transfer, 107, pp. 922–

929, 1985.

[36] Kasagi, N., Sumitani, Y., Suzuki, Y., and Iida, O. Kinematics of the quasi-coherent

vortical structure in near-wall turbulence, Int. J. Heat Fluid Flow, 16, pp. 2–10,

1995.

[37] Iida, O., Iwatsuki, M., and Nagano, Y. Vortical turbulence structure and transport

mechanism in a homogeneous shear ﬂow, Phys. Fluids, 12, pp. 2895–2905, 2000.

[38] Hattori, H., Ohiwa, N., Kozuka, M., and Nagano,Y. Improvement of nonlinear eddy

diffusivity model for rotational turbulent heat transfer at various rotating axes, Fluid

Dynam. Res., 41, 2009.

[39] Craft, T. J., Launder, B. E., and Suga, K. Development and application of a cubic

eddy-viscosity model of turbulence, Int. J. Heat Fluid Flow, 17, pp. 108–115, 1996.

[40] Nagano,Y., and Hattori, H.An improved turbulence model for rotating shear ﬂows, J.

Turbulence, 3, pp. 1–13, 2002.

[41] Gatski, T. B., and Speziale, C. G. On explicit algebraic stress models for complex

turbulent ﬂows, J. Fluid Mech., 254, pp. 59–78, 1993.

[42] Pope, S. B. A more general effective-viscosity hypothesis, J. Fluid Mech., 72,

pp. 331–340, 1975.

[43] Suga, K., and Abe, K. Nonlinear eddy viscosity modelling for turbulence and heat

transfer near wall and shear-free boundaries, Int. J. Heat Fluid Flow, 21, pp. 37–48,

2000.

[44] Younis, B. A., Speziale, C. G., and Clark, T. T., A Rational Model for the Turbulent

Scalar Fluxes, Proc. R. Soc. Lond. S. A, 461, pp. 575–594, 2005.

[45] Abe, K., Kondoh. T., and Nagano, Y. A two-equation heat-transfer model reﬂecting

second-moment closures for wall and freeturbulent ﬂows,Int. J. Heat Fluid Flow,17,

pp. 228–237, 1996.

Sunden CH008.tex 10/9/2010 15: 19 Page 330

330 Computational Fluid Dynamics and Heat Transfer

[46] Hishida, M., Nagano, Y., and Tagawa, M. Transport processes of heat and momen-

tum in the wall region of turbulent pipe ﬂow, Proc. 8th Int. Heat Transfer Conf.,3,

pp. 925–930, 1986.

[47] Kim, J., andMoin, P.Transportofpassivescalarsin aturbulentchannelﬂow,Turbulent

Shear Flows 6. J. C. André, J. Cousteix, F. Durst, B. E. Launder, F. W. Schmidt, and J.

H. Whitelaw, eds. Springer, Berlin, pp. 85–96, 1989.

[48] Hattori,H.,andNagano,Y.Calculationofturbulentﬂowswithpressuregradientsusing

ak-ε model,Trans. JSME, 59-560B, pp. 1043–11048, 1995.

Sunden CH009.tex 25/8/2010 10: 57 Page 331

9 Analytical wall-functions of turbulence for

complex surface ﬂow phenomena

K. Suga

Osaka Prefecture University, Sakai, Japan

Abstract

Therecentlyemergedanalyticalwall-function(AWF)methodsforsurfaceboundary

conditions of turbulent ﬂows are summarised. Since the AWFs integrate transport

equations of momentum and scalars over the control volumes adjacent to surfaces

withsomesimpliﬁcations,itiseasytoincludecomplexsurface-ﬂowphysicsintothe

wall-function formula. Hence, the AWF schemes are successful to treat turbulent

ﬂow and scalar transport near solid, smooth, rough and permeable walls. High

Prandtlor Schmidtnumber scalartransport nearwallsor freesurfaces arealso well

handled by the AWFs.This chapter, thus, summarises their rationale, fundamental

equations and procedures with illustrative application results.

Keywords:Analytical wall-function, High Prandtl number, High Schmidt number,

Permeable wall, Rough wall,Turbulent ﬂows

9.1 Introduction

WallfunctionshavebeenusedfromtheearlystageofturbulenceCFD.Sincenumer-

ical integ ration of turbulence equations down to a solid wall requires dense grid

nodes to resolve the steep variations of the turbulence quantities, it was virtually

impossibleforthepeoplein1970stoperformturbulenceCFDofengineeringﬂows

even by the most powerful computer in those days. Moreover, ﬂow physics very

near thewall (insidesublayer), whichis required for constructing amoreadvanced

turbulence model, was not well known.

However, according to the development of computers, many studies on low

Reynolds number (LRN) turbulence models have been made and such LRN mod-

els have replaced wall functions in most numerical studies (Launder [1]). The

emergence of direct numerical simulations (Kim, Moin and Moser [2]) enhanced

this tendency, and so many LRN turbulence models have been proposed since

then.

Sunden CH009.tex 25/8/2010 10: 57 Page 332

332 Computational Fluid Dynamics and Heat Transfer

Despite the fact that many LRN turbulence models perform satisfactorily,

industrial engineers still routinely make use of classical wall-function approaches

for representingnear-wall turbulenceand heattransfer(e.g.,Ahmedand Demoulin

[3]). One reason for this is that, even with advances in computing power, their

near-wall resolution requirements make LRN models prohibitively expensive in

complex three-dimensional industrial heat and ﬂuid ﬂows.

This is easily understandable when one considers ﬂows over rough and/or

porous surfaces, whichare common in industrialapplications.Because one cannot

hope to resolve the details of tiny elements composing the rough and/or porous

walls,thewall-functionapproach maybe theonlypracticalstrategyfor suchindus-

trial applications. Another difﬁculty of performing LRN models is treating scalar

ﬁelds of high Prandtl or Schmidt numbers. In such ﬂows, the sublayer thickness of

thescalaris muchthinnerthanthatoftheviscoussublayerofthe ﬂow.Thisrequires

much ﬁner grid nodes for the scalar ﬁelds than those for ﬂow ﬁelds.

The most part of the ‘standard’ log-law wall-function (LWF) strategies was

proposed in the 1970s with the assumption of semi-logarithmic variations of the

near-wall velocity and temperature (e.g. Launder and Spalding [4]). After the

establishment of the LWF, Chieng and Launder [5] improved the wall function

by allowing for a linear variation of both the shear stress and the turbulent kinetic

energy across the near-wall cell. Amano [6] also attempted to improve the wall

functions. However, all the above attempts were still based on the log-law and it

is well known that such a condition does not apply in ﬂows with strong pressure

gradients and separation (e.g. Launder [1, 7]).

Thus,severalattemptsfordevelopingnewwall-functionapproachesweremade.

Recently, Craft et al. [8] proposed an alternative wall-function strategy. While still

semi-empirical in nature, their model makes assumptions at a deeper, more gen-

eral level than the log-law based schemes. This approach is called the analytical

wall-function (AWF) and integrates simpliﬁed mean ﬂow and energy equations

analytically over the control volumes adjacent to the wall, assuming a near-wall

variation of the turbulent viscosity. The resulting analytical expressions then pro-

duce the value of the wall shear stress and other quantities which are required over

the nearwall cell.

Following this strategy, the present author and his colleagues discussed and

proposed extensions of the AWF approach that allow for the effects of ﬁne-grain

surface roughness, porous walls and a wide range ofPrandtland Schmidt numbers

[10–13].This chaptersummarises the outlines andthe application results

of those

extensions of the AWF method for complex surface turbulence.

Inthecontextof largeeddysimulations,CabotandMoin[9]discussedawallmodelwhose

basicideawassimilartothatoftheAWF, though itusedanimplicitformulaofthewallshear

stress.

Alltheresultspresentedhavebeencomputedbyin-houseﬁnitevolumecodeswhichemploy

the SIMPLE pressure-correction algorithm [14] with Rhie–Chow interpolation [15] and the

third-order MUSCL-type scheme (e.g. [16]) for convection terms.

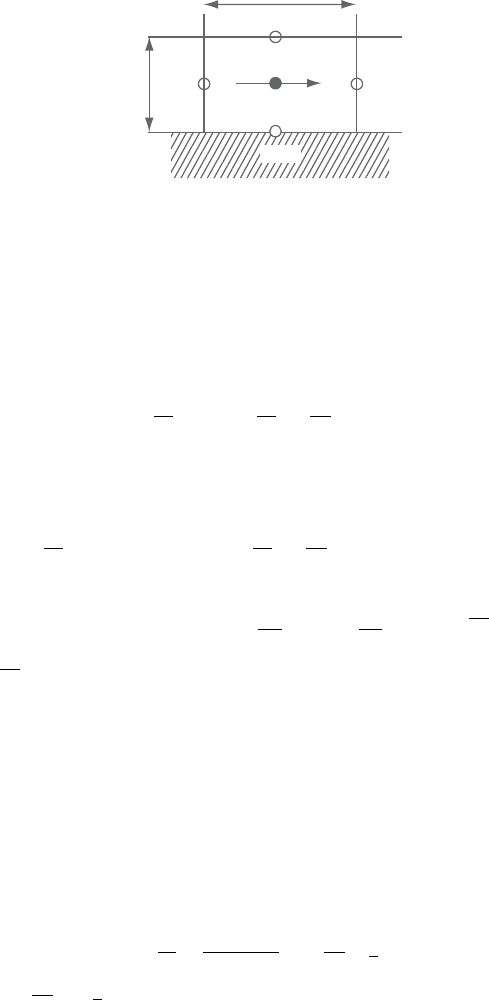
Sunden CH009.tex 25/8/2010 10: 57 Page 333

AWFs of turbulence for complex surface ﬂow phenomena 333

∆y

∆x

Wall

Figure 9.1. Near-wall grid arrangement.

9.2 Numerical Implementation of Wall Functions

In this section, we recall the main features of the implementation of the wall

functions into a numerical code.

A simpliﬁed transport equation for φ near walls:

∂

∂x

(ρUφ) =

∂

∂y



∂φ

∂y



+ S

(1)

can be integrated using the ﬁnite volume method over the cells illustrated in

Figure 9.1 giving

∂

∂x

(ρUφ)dx dy =

∂

∂y



∂φ

∂y



dx dy +

dx dy (2)

[(ρUφ)

− (ρUφ)

]y =





dφ



−



dφ





x +

xy (3)

where

is the averaged source term over the wall-adjacent cell P. Note that x

is the wall-parallel coordinate while y is the wall normal coordinate. (Although

two-dimensional forms are written here, extending them to three dimensions is

straightforward.)

When the wall-parallel component of the momentum equation is considered

(φ =U) the term (dφ/dy)

in equation (3) corresponds to the wall shear stress

, while in the energy equation it corresponds to the wall heat ﬂux q

. Instead

of calculating these from the standard discretization, they are obtained from the

algebraic wall-function expressions.

In the case ofthe transport equation for the turbulenceenergy k in incompress-

ible ﬂows, the averaged source term over the wall adjacent cell is written as:

= ρP

− ρε = ρ(P

−ε) (4)

The terms

and ε thus also need to be provided by the wall function. Note that

the wall function also can provide k and ε at P as the boundary conditions for their

transport equations.

Sunden CH009.tex 25/8/2010 10: 57 Page 334

334 Computational Fluid Dynamics and Heat Transfer

9.3 Standard Log-LawWall-Function (LWF)

BeforeintroducingtheAWF,thestandard wall functionapproach usingthe log-law

is surveyed brieﬂy.

The ﬁrst requirement, when using the standard wall function, is that the node

point P is sufﬁciently remote from the wall for y

to be much greater than that

of the viscous sublayer. The value, at least, greater than 30 (y

≥30) is normally

applied.Then, the ﬂuxes of momentum and thermal ﬁelds to the wallare supposed

to obey the following logarithmic proﬁles:

lny

+ B (5)

lny

+ C (6)

wheretheconstants κ =0.38 to 0.42 and κ

=0.47 to0.48.Theconstant B =5.0 to

5.5 while

C = (3.85Pr

1/3

− 1.3)

+ 1/κ

lnPr

for smooth wall cases.The wallshearstress τ

and heat ﬂux q

at the (N +1) step

of the iterative computation are then obtained as:

/ρ

(N+1)



lny

+ B



(N)

(7)

)

N+1



ρc

lny

+ C



(N)

(8)

In the local equilibrium boundary layers, the eddy viscosity formula gives

−

uv =ν

∂U/∂y, and thus the production of the turbulence kinetic energy k can

be written as:

=−uv

∂U

∂y

= ν

∂U

∂y



∂U

∂y



(9)

Then, since ν

/ε and P

=ε in local equilibrium,



−



(ν

∂U/∂y)

= c

(10)

Thus, using the following relation:

/ρ 

√

−uv 



1/2

k  c

1/4

1/2

(11)

The coefﬁcient c

can be obtained from the experimental results of local equilibrium

boundary layers: −

uv/k 0.3, as c

=(−uv)

=0.3

=0.09.

Sunden CH009.tex 25/8/2010 10: 57 Page 335

AWFs of turbulence for complex surface ﬂow phenomena 335

one can rewrite equation (7) as:

ρc

1/4

1/2

ln(c

1/4

∗

) +B

(12)

with the relation of y

1/4

∗

in local equilibrium [4]. Note that the super-

scripts meaning steps are omitted for simpliﬁcation hereafter. This form avoids

a shortcoming of using y

which becomes zero where the wall shear stress τ

vanishes.

For turbulence energy k, one can obtain its value at P from equation (11) as:

√

(13)

for the boundary condition.The dissipation rate of k is also given as:

κy

(14)

for the boundary condition at P by manipulating equations (10) and (11) with

the relation ν

/ν =κy

. Note that the friction velocity U

√

/ρ) should be

obtained from equation (7) or (12).

9.4 AnalyticalWall-Function (AWF)

9.4.1 Basic strategy of theAWF

In theAWF, the wall shear stress and heat ﬂux are obtained through the analytical

solution of simpliﬁed near-wall versions of the transport equations for the wall-

parallelmomentumandtemperature[8].Incaseoftheforcedconvectionregime,the

main assumption required for the analytical integration of the transport equations

is a prescribed variation of the turbulent viscosity µ

. The distribution of µ

over

the wall-adjacent cell P is modelled as in a one-equation turbulence model:

= ρc

1/2

 = ρc

1/2



y  αµy

∗

(15)

where istheturbulentlengthscale,α =c



andy

∗

≡yk

1/2

/ν.Inordertoconsider

viscous sub-layer effects, instead of introducing a damping function, the proﬁle of

is modelled as:

= max{0,αµ(y

∗

− y

∗

)} (16)

in which µ

is still linear in y

∗

and grows from the edge of the viscous sub-layer:

∗

(≡y

1/2

/ν).