Amano R.S., Sunden B. (Eds.) Computational Fluid Dynamics and Heat Transfer: Emerging Topics
Подождите немного. Документ загружается.


Sunden CH008.tex 10/9/2010 15: 19 Page 306
306 Computational Fluid Dynamics and Heat Transfer
On the other hand, substituting the integrity basis and the theoretical expres-
sions [42]:
T
(λ)
S
∗
+ S
∗
T
(λ)
−
2
3
{T
(λ)
S
∗
}I =
γ
H
λγ
T
(γ)
and
T
(λ)
W
∗
− W
∗
T
(λ)
=
γ
J
λγ
T
(γ)
where H and J are the scalar functions, into equation 30, gives the following
equation for T
(λ)
:
λ
Q
(λ)
T
(λ)
=−
λ
δ
1λ
T
(1)
−
λ
Q
(λ)
λ
H
λγ
T
(λ)
−
λ
J
λγ
T
(λ)
(33)
Equation (33)can bewritten as Q
(λ)
=A
−1
γλ
B
λ
, where A
γλ
=−δ
λγ
−H
λγ
+J
λγ
,
and B
λ
=δ
1λ
. By using Cayley–Hamilton identities, the matrices H
λγ
and J
λγ
can
be determined.Thus, we can obtain Q
(λ)
using Mathematica as follows:
Q
(1)
=−
1
2
(6 −3η
1
− 21η
2
− 2η
3
+ 30η
4
)/DQ
(6)
=−9/D
Q
(2)
=−(3 + 3η
1
− 6η
2
+ 2η
3
+ 6η
4
)/DQ
(7)
= 9/D
Q
(3)
= (6 −3η
1
− 12η
2
− 2η
3
− 6η
4
)/DQ
(8)
= 9/D
Q
(4)
=−3(3η
1
+ 2η
3
+ 6η
4
)/DQ
(9)
= 18D
Q
(5)
=−9/DQ
(10)
= 0
⎫
⎪
⎪
⎪
⎪
⎪
⎬
⎪
⎪
⎪
⎪
⎪
⎭
(34)
where
D =3 −
7
2
+ η
2
1
−
15
2
η
2
− 8η
1
η
2
+ 3η
2
2
− η
3
+
2
3
η
1
η
3
(35)
− 2η
2
η
3
+ 21η
4
+ 24η
5
+ 2η
1
η
4
− 6η
2
η
4
with η
1
={S
∗2
}, η
2
={W
∗2
}, η
3
={S
∗3
}, η
4
={S
∗
W
∗2
}, and η
5
={S
∗2
W
∗2
}.
In order to obtain reasonable forms for Q
(1)
∼Q
(9)
, we assume S
13
=W
13
=0.
Thus, η
3
and η
4
become 0 and η
5
=
1
2
η
1
η
2
. Therefore, the following reasonable
forms for Q
(1)
∼Q
(6)
can be derived:
Q
(1)
=−
3
3 −2η
1
− 6η
2
, Q
(2)
=−
3
3 −2η
1
− 6η
2
, Q
(3)
=
6
3 −2η
1
− 6η
2
Q
(4)
=
−18η
1
(3 −2η
1
− 6η
2
)(2 −η
1
− η
2
)
, Q
(5)
=
−18
(3 −2η
1
− 6η
2
)(2 −η
1
− η
2
)
Q
(6)
=
−18
(3 −2η
1
− 6η
2
)(2 −η
1
− η
2
)
⎫
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎬
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎭
(36)
Sunden CH008.tex 10/9/2010 15: 19 Page 307
Recent developments in DNS 307
Consequently, we can obtain the cubic NLEDM as follows:
b
∗
ij
=−
3
3 −2η
2
+ 6ζ
2
$
S
∗
ij
+ (S
∗
ik
W
∗
kj
− W
∗
ik
S
∗
kj
) −2
S
∗
ik
S
∗
kj
−
1
3
S
∗
mn
S
∗
nm
δ
ij
+
6
2 −η
2
+ ζ
2
η
2
(W
∗
ik
W
∗
kj
−
1
3
δ
ij
W
∗
mn
W
∗
nm
) +(W
∗
ik
S
∗
k
S
∗
j
− S
∗
ik
S
∗
k
W
∗
j
)
+
W
∗
ik
W
∗
k
S
∗
j
+ S
∗
ik
W
∗
k
W
∗
j
−
2
3
S
∗
m
W
∗
mn
W
n
δ
ij
%
(37)
where η =(S
∗
ij
S
∗
ij
)
1
2
, ζ =(W
∗
ij
W
∗
ij
)
1
2
, and b
∗
ij
, S
∗
ij
, and W
∗
ij
are nondimensional
quantities, respectively, redefined as follows:
b
∗
ij
= C
D
b
ij
, S
∗
ij
= C
D
τ
R
o
S
ij
, W
∗
ij
= 2C
D
τ
R
o
W
ij
(38)
Sincetheproposedmodelinequation(37)canbewrittenasthefollowing equa-
tionfortheReynoldsshearstress,
vw (orb
23
),instreamwiserotatingflow, inwhich
S
12
(=S
21
),W
12
(=−W
21
),S
23
(=S
32
),andW
23
(=−W
32
)exist,theReynoldsshear
stress,
vw, can be reproduced by the present model:
b
∗
23
=
3
3 −2η
2
+ 6ζ
2
$
S
∗
23
+
6
2 −η
2
+ ζ
2
[(W
∗
21
S
∗
12
S
∗
23
− S
∗
21
S
∗
12
W
∗
23
)
(39)
+(W
∗
21
W
∗
12
S
∗
23
+ W
∗
23
W
∗
32
S
∗
23
+ S
∗
21
W
∗
12
W
∗
23
+ S
∗
23
W
∗
32
W
∗
23
)]
%
In equation (37), the functions 3/(3−2η −2+6ζ
2
) and 6/(2−η
2
+ζ
2
)may
be taken to be a negative value or 0 with the increase in η.Thus, in order to avoid
taking a negative value or 0, we model these functions taking into account the
rotational effect as follows:
3
3 −2η
2
+ 6ζ
2
1
1 +
22
3
W
∗2
4
+
2
3
W
∗2
4
− S
∗2
− f
∗2
ω
f
B
+
2
3
f
∗2
ω
(40)
6
2 −η
2
+ ζ
2
3
1 +
3
2
W
∗2
4
+
1
2
W
∗2
4
− S
∗2
− f
∗2
ω
f
B
+
1
2
f
∗2
ω
(41)
where
f
B
= 1 +C
η
W
∗2
4
− S
∗2
− f
∗2
ω
(42)
f
∗2
ω
= (C
D
τ
R
o
)
2
[
m
(2ε
mji
W
ij
−
m
)]
2
(43)

Sunden CH008.tex 10/9/2010 15: 19 Page 308
308 Computational Fluid Dynamics and Heat Transfer
Themodelfunction, f
∗2
ω
,inequation(43)isintroducedtoavoidaninappropriate
value of (W
∗2
/4−S
∗2
) with the increase in a rotation number. Since f
∗2
ω
=0is
consistently kept in non rotational flows, inadequate Reynolds stresses predicted
by the proposed model are not given in non rotational flows.
Finally, in order to construct a precise model for rotational flow, a cubic term
introducedinanNLCLSmodel[40]isaddedintheproposedmodel.Consequently,
the final form of the present cubic NLEDM is given as follows:
u
i
u
j
=
2
3
kδ
ij
− c
1
ν
t
S
ij
+ c
2
k(τ
2
R
o
+ τ
2
R
w
)(S
ik
W
kj
− W
ik
S
kj
)
+ c
3
k(τ
2
R
o
+ τ
2
R
w
)
S
ik
S
kj
−
1
3
S
mn
S
mn
δ
ij
+ c
4
kτ
2
Ro
W
ik
W
kj
−
1
3
W
mn
W
mn
δ
ij
(44)
+ c
5
kτ
3
Ro
(W
ik
S
k
S
j
− S
ik
S
k
W
j
) +c
6
kτ
3
Ro
W
ik
W
k
S
j
+ S
ik
W
k
W
j
−
2
3
S
m
W
mn
W
n
δ
ij
+ c
7
kτ
3
Ro
(S
ij
S
k
S
k
− S
ij
W
k
W
k
)
where ν
t
=C
µ
f
µ
k
2
/ε and C
µ
=0.12, and the model functions and constants are
given as follows:
c
1
=−2/f
R1
, c
2
=−4C
D
/f
R1
, c
3
= 4C
D
/f
R1
c
4
=−8C
3
D
S
2
/(f
R1
f
R2
), c
5
= 4C
2
D
f
R
/(f
R1
f
R2
),
c
6
= 2C
2
D
/(f
R1
f
R2
), c
7
= 10C
2
µ
C
2
D
, C
D
= 0.8
f
R1
= 1 +(C
D
τ
Ro
)
2
[(22/3)W
2
+ (2/3)(W
2
− S
2
− f
2
ω
)f
B
]
f
R2
= 1 +(C
D
τ
Ro
)
2
[(3/2)W
2
+ (1/2)(W
2
− S
2
− f
2
ω
)f
B
]
f
R
= 12[1− exp(f
3/4
SW
/26)]
f
µ
= [1 −f
w
(32)]{1+ (40/R
3/4
t
)exp[−(R
tm
/35)
3/4
]}
f
B
= 1 +C
η
(C
D
τ
Ro
)
2
(W
2
− S
2
− f
2
ω
)
f
2
ω
=
m
(2ε
mji
W
ij
−
m
), C
η
= 5.0
⎫
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎬
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎪
⎭
(45)
The characteristic time-scale τ
R
w
is introduced in an NLHN model [38] for an
anisotropy and wall-limiting behavior of turbulent intensity defined as:
τ
R
w
=
<
1
6
f
R1
/C
D
f
SW
1 −
3C
v1
f
v2
8
f
2
v1
(46)
Sunden CH008.tex 10/9/2010 15: 19 Page 309
Recent developments in DNS 309
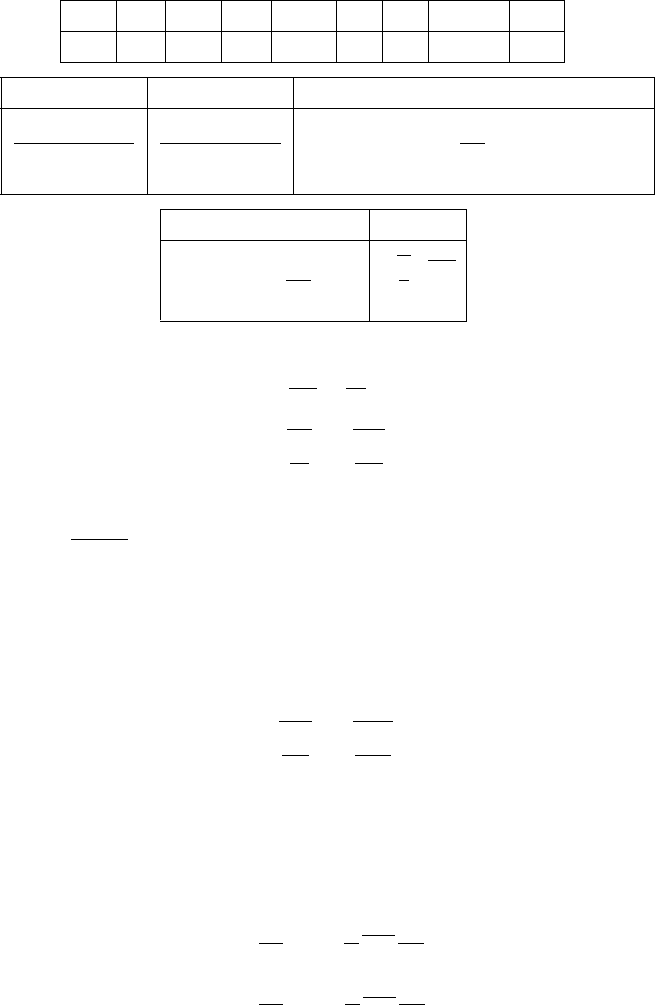
Table 8.6. Model constants and functions of transport equations for k and ε
C
ε1
C
ε2
C
ε3
C
ε4
C
ε5
C
s
C
ε
C
C
f
1.45 1.9 0.02 0.5 0.015 1.4 1.4 −0.045 6.0
f
t1
f
t2
f
ε
1 +9f
w
(8)
[1 −f
w
(32)]
1/2
1 +5f
w
(8)
[1 −f
w
(32)]
1/2
=
1 −0.3exp
−
R
t
6.5
2
>
[1 −f
2
w
(3.7)]
f
R
C
f
exp
−
R
10
0.2
?
ν
ε
f
SW
f
SW
=
W
2
2
+
S
2
3
− f
SW
(47)
f
SW
=
⎡
⎣
⎛
⎝
<
S
2
2
−
<
W
2
2
⎞
⎠
f
w
(1)
⎤
⎦
2
(48)
where C
v1
=0.4, C
v2
=2.0×10
3
, f
v1
= exp[−(R
tm
/45)
2
] and f
v2
=1−
exp(−
√
R
t
/C
v2
).Thewallreflectionfunctionisdefinedbyf
w
(ξ)=exp[−(R
tm
/ξ)
2
],
and the corrected Reynolds number for the rotating flow is given as
R
tm
=(C
tm
n
∗
R
1/4
t
)/(C
tm
R
1/4
t
+ n
∗
)withC
tm
=1.3×10
2
[38].Moreover,itisfound
fromtheevaluationshowninFigures8.28fand8.29fthatthewall-limitingbehavior
ofReynoldsstresscomponentisnotsatisfied forthetested rotatingflows.Thus,the
modelfunctionin equation(48)ofcharacteristic time-scaleτ
R
w
isslightlymodified
as follows:
f
SW
=
<
S
∗2
2
−
<
W
∗2
2
f
w
(1)
2
(49)
where S
∗
=ε
mn
S
mn
, W
∗
=ε
mn
W
mn
.
For the modeled transport equations of k and ε as indicated in equations (9)
and (10), the turbulent diffusion and the pressure diffusion terms are modeled as
follows [38]:
T
k
=
∂
∂x
j
C
s
f
t1
ν
t
k
u
j
u
∂k
∂x
(50)
T
ε
=
∂
∂x
j
C
ε
f
t2
ν
t
k
u
j
u
∂ε
∂x
(51)
Sunden CH008.tex 10/9/2010 15: 19 Page 310
310 Computational Fluid Dynamics and Heat Transfer
k
= max
$
−0.5ν
∂
∂x
j
k
ε
∂ε
∂x
j
f
w
(1)
,0
%
(52)
ε
= C
ε4
∂
∂x
j
$
[1 −f
w
(5)]
ε
k
∂ε
∂x
j
f
w
(5)
%
(53)
The extra term in the ε-equation is adopted as the identical to the NLHN
model [38]:
E = C
ε3
ν
k
ε
u
j
u
∂
2
U
i
∂x
∂x
k
∂
2
U
j
∂x
∂x
k
+ C
ε5
ν
k
ε
∂
u
j
u
k
∂x
j
∂U
i
∂x
k
∂
2
U
i
∂x
j
∂x
k
(54)
Finally, a rotation-influenced addition ter m, R, in the ε-equation (10) is
generalized as follows:
R = C
f
k!
ij
W
ij
d
(55)
whered
istheunitvectorinthe spanwisedirection.Modelconstants andfunctions
in the k- and ε-equations are indicated in Table 8.6. In what follows, we call the
cubic NLEDM, thus obtained, a nonlinear eddy diffusivity for momentum model
(NLEDMM).
8.8 Nonlinear Eddy Diffusivity Model forWall-Bounded
Turbulent HeatTransfer
8.8.1 Evaluations of turbulent heat transfer models in rotating
channel flows
Toimprovethenonlineareddydiffusivityforheatmodel(NLEDHM),thefollowing
nonlinear turbulence models are evaluated using DNS data (refer to the detailed
model functions and constants of each models in Refs. [38], [43], and [44]).
•
Nagano and Hattori [38] (hereinafter referred to as NLHN)
u
j
θ =−α
t
jk
∂
∂x
k
+
C
θ1
f
RT
τ
2
mo
u
u
k
C
θ2
S
j
+ C
θ3
W
j
+ 2C
θ1
ε
jm
m
∂
∂x
k
(56)
where α
t
jk
is an anisotropic eddy diffusivity tensor for heat as follows:
α
t
jk
=
C
∗
θ1
f
RT
u
j
u
k
τ
m
(57)
•
Suga and Abe [43] (hereinafter referred to as NLSA)
u
i
θ =−C
θ
kτ(σ
ij
+ α
ij
)
∂
∂x
j
(58)
Sunden CH008.tex 10/9/2010 15: 19 Page 311
Recent developments in DNS 311
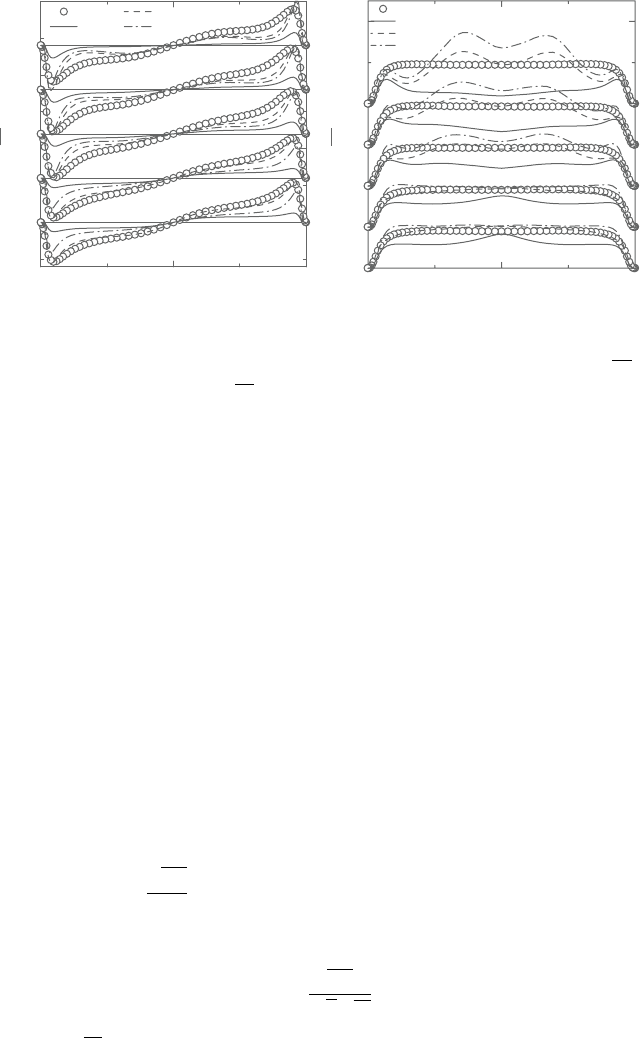
0 1
y/δ
2
−6
0
0
0
0
Ro
τ
=0.1
Ro
τ
=0.1
Ro
τ
=0.04
Ro
τ
=0.04
Ro
τ
=0.02
Ro
τ
=0.02
Ro
τ
=0.01
Ro
τ
=0.01
6
DNS
NLHN
NLYSC
NLSA
0 1 2
0
0
0
0
1
DNS
NLHN
NLSA
NLYSC
(a)
y/δ
(b)
uθ
+
υθ
+
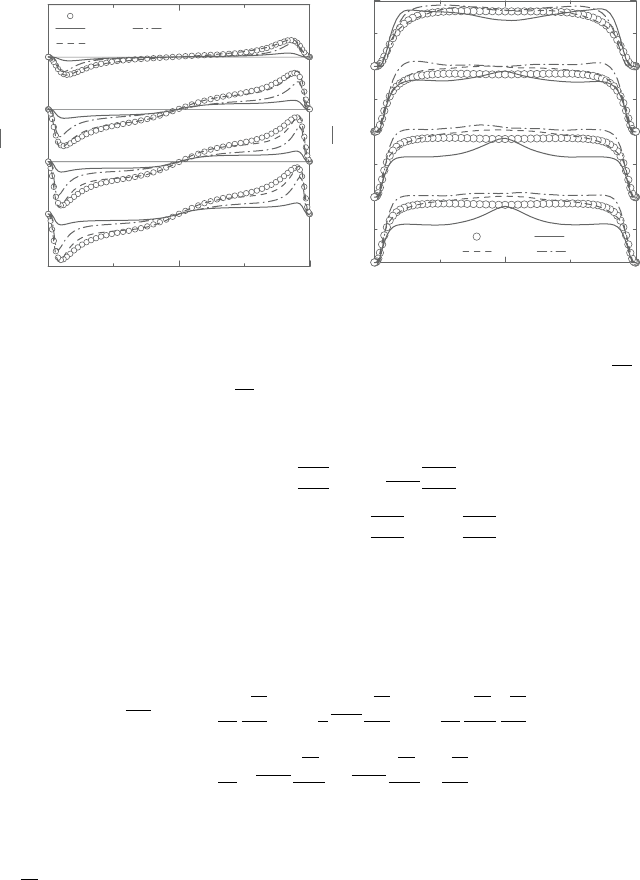
Figure 8.30. Evaluations of turbulent heat fluxes (Case 1); (a) streamwise (uθ),
(b) wall-normal (
vθ).
where
σ
ij
= C
σ0
δ
ij
+ C
σ1
u
i
u
j
k
+ C
σ2
u
i
u
u
u
j
k
,
α
ij
= C
α0
τW
ij
+ C
α1
τ
W
i
u
u
j
k
+ W
j
u
i
u
k
Notethat theoriginalmodelis describedinthe nonrotationalform[43]. Inorder
toevaluatetheNLSAmodel intherotationalflow, thevorticitytensoris replaced
with the absolute vorticity tensor in the model.
•
Younis et al. [44] (hereinafter referred to as NLYSC)
u
i
θ =−C
1
k
2
ε
∂
∂x
i
− C
2
k
ε
u
i
u
j
∂
∂x
j
− C
3
k
3
ε
2
∂U
i
∂x
j
∂
∂x
j
(59)
−C
4
k
2
ε
2
u
i
u
k
∂U
j
∂x
k
− u
j
u
k
∂U
i
∂x
k
∂
∂x
j
Note that the above description is in the original model form [44]. In order to
apply to the model evaluation in rotating channel flow, the velocity gradient,
∂
U
i
/∂x
j
, must be replaced with S
ij
+W
ij
in the model. However, the evaluation
is conductedusing theoriginal form, because we shouldknowthe adverse effect
of using it.
Evaluationresults are shown in Figures 8.30 and 8.31. In Case 1, it can beseen
that the NLSA model accurately reproduces the streamwise heat flux at various
rotationnumbers, because theNLSAmodel was improvedinorder toproperlypre-
dictthestreamwise turbulentheat flux[43].As foran evaluationfor aprediction of
Sunden CH008.tex 10/9/2010 15: 19 Page 312
312 Computational Fluid Dynamics and Heat Transfer
0
DNS
DNS
NLSA
NLSA
0
0
0
0
0
(a)
y/δ
Ro
τ
=1.0
Ro
τ
=2.5
Ro
τ
=7.5
Ro
τ
=10
Ro
τ
=15
Ro
τ
=1.0
Ro
τ
=2.5
Ro
τ
=7.5
Ro
τ
=10
Ro
τ
=15
12
0
(b)
y/δ
12
−6
6
NLHN
NLHN
NLYSC
NLYSC
uθ
+
2
0
0
0
0
υθ
+
Figure 8.31. Evaluations of turbulent heat fluxes (Case 2); (a) streamwise (uθ),
(b) wall-normal (
vθ).
wall-normalheatflux, theNLHNmodelslightlyunderpredictsincaseof thelowest
rotation number, but the NLHN model gives good agreement with DNS data with
increaseinrotationnumber.InCase2,theNLSAandNLYSCgiveadequatepredic-
tionsofbothturbulentheatfluxesincaseofthelowestrotationnumber.Eventhough
the NLYSC does not employ the rotational form, it is noteworthy that the NLYSC
model nearly gives equivalent results in comparison with the NLSA model. How-
ever,itisobviousthatallmodelscannotpredictDNSresultswithincreaseinrotation
number.Inparticular, thewall-normalturbulentheatfluxisnotreproducedbyeval-
uated models in case of the highest rotation number. From this evaluation of Case
2, it may be concluded that the mean temperature cannot be adequately predicted
using evaluated models. Thus, the model should be improved to accurately predict
heated channel flows with arbitrary rotating axes and various rotation numbers.
8.8.2 Proposal of nonlinear eddy diffusivity model for wall-bounded
turbulent heat transfer
The formulation of nonlinear eddy diffusivity for a heat model (NLEDHM) is
derived below [39].The transport equation for turbulent heat flux is written:
D
u
j
θ
Dt
= D
jθ
+ T
jθ
+ P
jθ
+
jθ
− ε
jθ
+ C
jθ
(60)
where we introduce the nondimensional heat-flux parameter a
∗
j
[45]:
a
∗
j
=
u
j
θ
√
k
√
k
θ
(61)
where k
θ
=θ
2
/2.
Sunden CH008.tex 10/9/2010 15: 19 Page 313
Recent developments in DNS 313
Thetransportequationfora
∗
j
isderivedtoneglectthediffusiveeffectsasfollows:
Da
∗
j
Dt
=
D
Dt
u
j
θ
√
k
√
k
θ
=
1
√
k
√
k
θ
Du
j
θ
Dt
−
1
2
u
j
θ
√
k
√
k
θ
1
k
Dk
Dt
+
1
k
θ
Dk
θ
Dt
=
1
√
k
√
k
θ
P
jθ
+
jθ
− ε
jθ
+ C
jθ
(62)
−
1
2
u
j
θ
√
k
√
k
θ
ε
k
P
k
ε
− 1
+
ε
θ
k
θ
P
k
θ
ε
θ
− 1
where the transport equations for k and k
θ
[see equations (9) and (11)] are
employed.
The most general linear expression is adopted for the modeled pressure–
temperature gradient correlation term,
jθ
, and dissipation term, ε
jθ
:
jθ
− ε
jθ
=−C
1
u
j
θ
τ
u
+ C
2
u
k
θ
∂
U
j
∂x
k
+ C
3
u
k
θ
∂
U
k
∂x
j
(63)
where τ
u
=k/ε.
The production and Coriolis terms in equation (60) are given by:
P
jθ
=−u
j
u
k
∂
∂x
k
− u
k
θ
∂
U
j
∂x
k
(64)
C
jθ
=−2ε
jmk
m
u
k
θ (65)
Therefore, the first term on the right-hand side of equation (62) is expanded as
follows:
1
√
k
√
k
θ
(P
jθ
+
jθ
− ε
jθ
+ C
jθ
) =
1
√
k
√
k
θ
C
1
τ
u
−
u
j
θ −
1
C
1
τ
u
u
j
u
k
∂
∂x
k
(66)
−
1 −C
2
C
1
τ
u
u
k
θ
∂
U
j
∂x
k
+
C
3
C
1
τ
u
u
k
θ
∂
U
k
∂x
j
−
2
C
1
τ
u
ε
jmk
m
u
k
θ
wherethemodelconstantsinequation(66)arereplacedasC
T1
=1/C
1
,C
T2
=(1−
C
2
)/C
1
, and C
T3
=C
3
/C
1
.Thus:
1
√
k
√
k
θ
(P
jθ
+
jθ
− ε
jθ
+ C
jθ
) =
1
√
k
√
k
θ
1
C
T1
τ
u
−
u
j
θ −C
T1
τ
u
u
j
u
k
∂
∂x
k
−
(
C
T2
− C
T3
)
τ
u
u
k
θS
jk
−
(
C
T2
+ C
T3
)
τ
u
u
k
θ
W
jk
+
2C
T1
C
T2
+ C
T3
ε
jmk
m
(67)
Sunden CH008.tex 10/9/2010 15: 19 Page 314
314 Computational Fluid Dynamics and Heat Transfer
Consequently, substituting equation (67) for equation (62), the following
equation is obtained:
Da
∗
j
Dt
=
1
√
k
√
k
θ
1
C
θ1
τ
u
−
u
j
θ −C
θ1
τ
u
u
j
u
k
∂
∂x
k
− C
θ2
τ
u
u
k
θS
jk
−C
θ3
τ
u
u
k
θ (W
jk
+ C
θ4
!
jmk
m
)
(68)
−
1
2
u
j
θ
√
k
√
k
θ
ε
k
P
k
ε
− 1
+
ε
θ
k
θ
P
k
θ
ε
θ
− 1
where C
θ1
=C
T1
, C
θ2
=C
T2
−C
T3
, C
θ3
=C
T2
+C
T3
, and C
θ4
=2C
T1
/
(C
T2
+C
T3
).
In the local equilibrium state, the following relation holds:
Da
∗
j
Dt
= 0 (69)
With the above condition of equation (69), equation (68) becomes as follows:
u
j
θ
√
k
√
k
θ
1
τ
u
1 +
C
θ1
2
P
k
ε
− 1
+
C
θ1
2R
P
k
θ
ε
θ
− 1
(70)
=−(δ
jk
+ 3b
jk
)
2
3
C
θ1
k
√
k
√
k
θ
∂
∂x
k
− (C
θ2
S
jk
+ C
θ3
W
jk
)
u
k
θ
√
k
√
k
θ
where W
jk
=W
jk
+C
θ4
!
jmk
m
, and the following characteristic time-scale in the
left-hand side of equation (70) is replaced with the mixed time-scale τ
m
for the
near-wall treatment:
τ
u
1 +
C
θ1
2
P
k
ε
− 1
+
C
θ1
2R
P
k
θ
ε
θ
− 1
→ τ
m
(71)
Finally, if we introduce the nondimensional given by the following equations:
b
∗
jk
= 3b
jk
,
∗
k
=
2
3
C
θ1
kτ
m
√
k
√
k
θ
∂
∂x
k
,
S
∗
jk
= C
θ2
τ
m
S
jk
,
W
∗
jk
= C
θ3
τ
m
W
jk
.
⎫
⎪
⎪
⎪
⎪
⎪
⎪
⎬
⎪
⎪
⎪
⎪
⎪
⎪
⎭
(72)
Thus, equation (70) becomes:
a
∗
j
=−(δ
jk
+ b
∗
jk
)
∗
k
− (S
∗
jk
+ W
∗
jk
)a
∗
k
(73)
Sunden CH008.tex 10/9/2010 15: 19 Page 315
Recent developments in DNS 315
Thus, we obtain the following explicit expression for the nondimensional
turbulent heat flux [45]:
a
∗
j
=
1
1 +
1
2
W
∗2
− S
∗2
[−δ
jk
− b
∗
jk
+ (S
∗
jk
+ W
∗
jk
) +(S
∗
j
+ W
∗
j
)b
∗
k
]
∗
k
(74)
where W
∗2
=W
∗
ij
W
∗
ij
and S
∗2
=S
∗
ij
S
∗
ij
. The derived equation (74) can be rewritten
in the conventional form as follows:
u
j
θ =−
C
θ1
τ
m
f
RT
u
j
u
k
∂
∂x
k
+
C
θ1
τ
2
m
f
RT
u
k
u
C
θ2
S
j
∂
∂x
k
+ C
θ3
W
j
∂
∂x
k
+ 2C
θ1
!
jm
m
∂
∂x
k
(75)
where C
θ4
=2C
θ1
/C
θ3
and f
RT
=1+
1
2
τ
2
m
(C
2
θ3
W
2
− C
2
θ2
S
2
), and the first term of
right-hand side can be rewritten using the following anisotropic eddy diffusivity
tensor for heat:
α
t
jk
=
C
θ1
f
RT
u
j
u
k
τ
m
(76)
Thus, the final form for NLEDHM given in equation (56) is obtained as
follows:
u
j
θ =−α
t
jk
∂
∂x
k
+
C
θ1
f
RT
τ
2
m
u
k
u
(C
θ2
S
j
+ C
θ3
W
j
+ 2C
θ1
ε
jm
m
)
∂
∂x
k
(77)
Based on the foregoing, the NLEDHM should be improved to accurately
predict heatedchannel flows with arbitrary rotating axes andvarious rotationnum-
bers. Although the NLHN properly predicts the rotating heated channel flow with
arbitrary rotating axes, the streamwise turbulent heat flux is slightly underpre-
dicted.Therefore,inordertoconstructaturbulencemodelhavinghigher-prediction
precision, we reconstruct the NLEDHM based on the NLHN model [38].
As for a prediction of streamwise turbulent heat flux, Hishida et al. [46] pro-
posed the relation −
uθ =C
h
(−uv/k)vθ from an experimental result, and Hattori
et al. [24] proposed the modified temperature–pressure gradient correlation and
dissipation terms for a buoyancy-affected thermal field, in which the prediction
precision of NLEDHM is improved. In this study, we introduce the dimensionless
Reynolds stress tensor A
ij
(=u
i
u
j
/k) in an anisotropic eddy diffusivity tensor for
heat as indicated in equation (60), which is adopted in the NLSA model [43] to
adequately predict the streamwise turbulent heat flux, for the NLHN model indi-
cated in equation [56].Also, introducing the dimensionless Reynolds stress tensor
