Amano R.S., Sunden B. (Eds.) Computational Fluid Dynamics and Heat Transfer: Emerging Topics
Подождите немного. Документ загружается.

Sunden CH008.tex 10/9/2010 15: 19 Page 276
276 Computational Fluid Dynamics and Heat Transfer
has become a powerful tool for in-depth investigation of the structure of turbu-
lent shear flows. This progress is mainly due to the considerable improvement in
computationalpowerofsupercomputersandthegreatefficiencyofnumericalmeth-
ods.Withtheadventofnewmassivelyparallelcomputers,thiscomputationalpower
isstillcontinuouslyincreasingandDNSofmoderatelyhighReynoldsnumberflows
in complex geometries has been becoming a reality. One distinct advantage of the
DNStechnique isreadyand accurateinformationsuch asthepressurefluctuationp
anddissipationrateε ofturbulentkineticenergyk,whichcanneverbeobtainedfrom
themeasurementsthathaveplayedthecentralroleintraditionalturbulenceresearch.
DNS hasalso contributed tothe development ofturbulence models. Especially,
two-equation (i.e., k −ε for a velocity field and k
θ
−ε
θ
for a thermal field, where
k and ε are the turbulent kinetic energy and its dissipation rate, and k
θ
and ε
θ
the intensity of fluctuating temperature and its dissipation rate, respectively) and
second-moment closure (i.e., Reynolds stress andturbulentheatflux) models have
made rapid progress with the aid of DNS. It is well known that the standard two-
equation and second-moment closure models provide comparatively satisfactory
results for simple flow fields, whereas in more complicated flow results are not as
satisfactory as initially expected. Thus, constructing a more sophisticated turbu-
lence model applicable to various types of flows is the central issue.
Inthis chapter, wefirst discussthetrend inrecent DNSresearchand itsapplica-
bility to turbulence model construction or evaluation.Then, we show two types of
DNSs, one is conducted using the highly accurate finite-differencemethod and the
other performed using the spectral method. Both DNSs mimic complex turbulent
flows with a high degree of accuracy. And finally, we intend to introduce our latest
turbulence models used inthe velocity and thermal fields of technological interest.
In addition, we introduce some new methods of evaluation and construction of
turbulence models and attempt to comment on future research.
8.2 Present State of Direct Numerical Simulations
At present, DNSiswidely regarded as anew method inplace of experimentsusing
apparatus. Since various information that can never be obtained from experiments
is immediately and accurately supplied by DNS, DNS is expectedto help establish
new turbulence theories, analyze turbulence phenomena, and construct universal
turbulence models. To establish turbulence theories and analyze turbulence phe-
nomena, Robinson [1] conducted thorough investigations using the DNS database
on boundary layer flow. Previous DNS studies were compiled and reviewed by
Kasagi [2], especially the relation between velocity and thermal fields.
From the viewpoint of turbulence modelers, there is much more interest in the
role of DNS in constructing a universal turbulence model. For example, detailed
information on fundamental turbulence quantities such as the pressure fluctuation
p and the dissipation rate ε have brought to light many problems inherent to the
existing turbulence models and paved the way for the construction of a universal
turbulence model.Also, information on budget profiles of various transport equa-
tionshaveencouragedactivemodelingoftheelementalprocessesofturbulence[3].
Sunden CH008.tex 10/9/2010 15: 19 Page 277
Recent developments in DNS 277
As a result, DNS has emerged as the most important tool for the development of
turbulence model.
On the other hand, some new attempts to construct the turbulence model with
the aid of the DNS databases have been suggested. Nagano and Shimada [4],
for example, have devised a method for evaluating a modeled-transport equation
itselfusingDNSdata.Thismethodalsohastheadvantageofindividuallyestimating
elemental processes of turbulence.
Early DNS research mainly aimed to consolidate the foundation of numerical
techniques under simple flow conditions, e.g., homogeneous shear flow [5], two-
dimensional channel flow [6, 7], and turbulent boundary layer flow [8]. Recent
DNS researchfocuses on theanalysesof turbulence phenomena(e.g., mechanisms
of turbulence generation and destruction, the interaction between inner and outer
layers, and the interaction between velocity and thermal fields). Moreover, DNS
has made it possible to construct databases under more complicated flow condi-
tions. Examples include adverse-pressure-gradient boundary layer flow [9, 10],
backward-facingstepflow[11], channelflowwith riblets [12,13], rotatingchannel
flow [14]–[18],square ductflow[19], channelflowwith injectionand suction[20],
channel flow under stable and unstable stratifications [21], impinging jet [22], and
stable and unstable turbulent thermal boundary layer [23], all of which introduce
highlyadvancedDNStechniques.DNSdatabasespresentedabovearenowavailable
for assessing various kinds of turbulence models.
8.3 Instantaneous and Reynolds-Averaged Governing
Equations for Flow and HeatTransfer
In DNS of turbulent motion, the three-dimensional unsteady Navier–Stokes equa-
tions for an incompressible fluid are solved directly for the instantaneous values of
the velocity components and pressure. Here, we consider a turbulent heated chan-
nel flow with rotation at a constant angular velocity as shown in Figure 8.1. The
governingequationsforanincompressiblerotatingchannelflowinreferenceframe
rotational coordinates can be described in the following dimensionless forms:
∂u
+
i
∂x
+
i
= 0 (1)
Du
+
i
Dt
+
=−
∂p
+
eff
∂x
+
i
+
1
Re
τ
∂
2
u
+
i
∂x
+
j
∂x
+
j
− ε
ik
Ro
τk
u
+
+
∗
1
(2)
Dθ
+
Dt
+
=
1
PrRe
τ
∂
2
θ
+
∂x
+
j
∂x
+
j
(3)
where t
+
(=tu
τ
/δ) is the time, u
+
i
(=u
i
/u
τ
) is the instantaneous velocity in
x
+
i
(=x
i
/δ) direction, θ
+
(=θ/ ) is the instantaneous temperature. These are
normalized by the friction velocity, u
τ
, the channel half width, δ, and the temper-
ature difference, (=
H
−
c
), between upper (
c
) and lower (
H
) walls.

Sunden CH008.tex 10/9/2010 15: 19 Page 278
278 Computational Fluid Dynamics and Heat Transfer
Cooled wall
Heated wall
x
3
x
2
x
1
2δ
Θ
c
Θ
H
Ω
3
Ω
2
Ω
1
Flow
Figure 8.1. Heated rotating channel with arbitrar y rotating axes.
The Reynolds-, the rotation-, and Prandtl numbers are respectively defined as
Re
τ
=u
τ
δ/ν,Ro
τk
=2
k
δ/u
τ
, and Pr=ν/α, where ν is the kinematic diffusivity
for momentum,
k
is the angular velocity with x
k
axis and α is the thermal dif-
fusivity for heat. The centrifugal force can be included in the effective pressure
p
+
eff
(=p
+
s
−Ro
2
r
2
c
/8), if fluid properties are constant, where p
+
s
is the normal-
ized static pressure, Ro=(Ro
j
Ro
j
)
1/2
is the absolute rotation number, and r
c
is
the dimensionless distance from the rotating axis [17].
∗
1
is the nondimensional
constant mean pressure gradient to maintain a flow, which isimplementedonly for
a flow with asymmetrically roughened walls at Ro=0 to make calculations more
stable.As described later, thespectral method [16]isused for theDNSs of rotating
channel flows. The computational conditions are listed in Table 8.1. The bound-
ary conditions are non-slip conditions for the velocity field and different constant
temperatures for the ther mal field on the walls, =constant, as well as periodic
conditions in the streamwise and spanwise directions.
In turbulence modeling, the so-called Reynolds-averaged equations are usu-
allyemployed, and turbulence models based on Reynolds-averaged Navier–Stokes
equationareoftenreferredtoasRANSmodels.ThegoverningequationsforRANS
turbulence model can be written as follows [24]:
∂
U
i
∂x
i
= 0 (4)
D
U
i
Dt
=−
1
ρ
∂
P
eff
∂x
i
+
∂
∂x
j
ν
∂
U
i
∂x
j
− u
i
u
j
− 2ε
ik
k
U
(5)
D
Dt
=
∂
∂x
j
α
∂
∂x
j
−u
j
θ
(6)
u
i
u
j
=
2
3
kδ
ij
− 2C
0
ν
t
S
ij
+ Nonlinear terms (7)
u
j
θ =−α
t
jk
∂
∂x
k
+ Nonlinear terms (8)
where C
0
is a model constant, k(=u
i
u
i
/2) is turbulent kinetic energy,
S
ij
[=(∂U
i
/∂x
j
+∂U
j
/∂x
i
)/2] is the strain tensor, U
i
is the mean velocity in x
i
Sunden CH008.tex 10/9/2010 15: 19 Page 279
Recent developments in DNS 279
Table 8.1. Methods for direct numerical simulation
Grid Regular grid
Time advancement
Viscosity term Crank–Nicolson method
Other terms Adams–Bashforth method
Spatial scheme Spectral method
Grid points (x
1
×x
2
×x
3
) 64×65×64
Computational volume 4πδ ×2δ ×2πδ
direction, α
t
jk
=−C
t0
u
j
u
k
τ
m
is the anisotropy eddy diffusivity for heat, is the
mean temperature, ν
t
=C
µ
f
µ
(k
2
/ε) is the eddy diffusivity for momentum, ρ is
density, and τ
m
is the hybrid/mixed time scale.
Thetransportequationsofturbulencequantities, i.e.,turbulentkineticenergy, k,
dissipationrateofturbulentkinetic energy, ε, temperature variance, k
θ
(=θ/2), and
dissipation rate of temperature variance, ε
θ
, which compose the eddy diffusivities
are given as follows [16]:
Dk
Dt
= ν
∂
2
k
∂x
j
∂x
j
+ T
k
+
k
+ P
k
− ε (9)
Dε
Dt
= ν
∂
2
ε
∂x
j
∂x
j
+ T
ε
+
ε
+
ε
k
(C
ε1
P
k
− C
ε2
f
ε
ε) +E + R (10)
Dk
θ
Dt
= α
∂
2
k
θ
∂x
j
∂x
j
+ T
k
θ
+ P
k
θ
− ε
θ
(11)
Dε
θ
Dt
= α
∂
2
ε
θ
∂x
j
∂x
j
+ T
ε
θ
+
ε
θ
k
θ
(C
P1
f
P1
P
k
θ
− C
D1
f
D1
ε
θ
)
(12)
+
ε
θ
k
(C
P2
f
P2
P
k
− C
D2
f
D2
ε) +E
θ
+ R
θ
where T
k
,T
ε
,T
k
θ
, and T
ε
θ
are turbulent diffusion terms,
k
and
ε
are pressure
diffusion terms, and P
k
(=−u
i
u
j
∂U
i
/∂x
j
) and P
k
θ
(=−u
j
θ∂ /∂x
j
) are production
terms, E andE
θ
areextratermstocorrect thenear-wallbehaviorsofε and ε
θ
, andR
and R
θ
are rotation-influenced additional terms. Note that, in the rotational coordi-
natesystem,thevorticitytensor,
ij
[=(∂U
i
/∂x
j
−∂U
j
/∂x
i
)/2],shouldbereplaced
with the absolute vorticity tensor in equations (7) and (8), i.e., W
ij
=
ij
+ε
mji
m
to satisfy the material frame indifference (MFI) [25].
8.4 Numerical Procedures of DNS
In general, the DNSs are performed using the two methods described briefly
in the following. Each method has its own special feature. Thus, between the
two approaches one should decide which to choose after careful consideration of
problems to be solved.

Sunden CH008.tex 10/9/2010 15: 19 Page 280
280 Computational Fluid Dynamics and Heat Transfer
Cooled wall T
w
= T
c
Heated wall T
w
= T
S
y
0
z
S
W
H
x
4.8δ
3.2δ
2δ
Figure 8.2. Channel with transverse-rib roughness and coordinate system.
8.4.1 DNS using high-accuracy finite-difference method
To solve a flow problem in complex geometries, a high-accuracy finite-difference
method is the best choice. Figure 8.2 shows a schematic of the channel with
transverse-rib roughness and the coordinate system used in the present study [13].
This type of flow is definitely complicated. The origin of the coordinate axes is
located in the middle of the enclosure between the ribs. Table 8.2 summarizes
some details of the high-accuracy finite-difference method. DNS was carried out
with a constant mean pressure gradient to balance the wall shear stress on both
walls.Note thatafullyconsistent andconservativefinite-differencemethodis used
for the convective term of the Navier–Stokes equation [26]. In order to solve the
Poisson equation for the pressure, the standard SOR method is applied and the
over-relaxation coefficient is set to 1.5. The adequate numbers of grid points are
arranged in each direction for DNS so as to exactly capture the turbulent heat
transfer as listed inTable 8.2. Especially, the grid resolution of spanwise direction,
z
∗
,mustbearrangedsmallerthan10.0.Thetimeadvancementist
∗
=1×10
−4
,
and the total time steps needed for the statistical quantities to converge reasonably
are 300,000. The numerical scheme used in this study is validated by comparing
the statistical quantities, including the budget of the turbulent kinetic energy, in
plane channel flow with those calculated by Nagano and Hattori [16], employing a
spectral method as described next.
8.4.2 DNS using spectral method
Referring to Kim et al. [6], a fourth-order partial differential equation for v (wall-
normal velocity component), a second-order partial differential equation for the
wall-normal component of vorticity, and the continuity equation are solved to
obtain the instantaneous flow field. The numerical method is fully described by
Kim et al. [6]. That is, a spectral method is adopted with Fourier series in the
streamwise and spanwise directions and Chebyshev polynominal expansion in the
wall-normal direction. The collocation grid used to compute the nonlinear terms
in physical space has 1.5 times finer resolution in each direction to remove alias-
ing errors (sometimes referred to as padding or 3/2-rule). For time integration,

Sunden CH008.tex 10/9/2010 15: 19 Page 281
Recent developments in DNS 281
Table 8.2. Computational methods
Channel with transverse-rib roughness
Grid Staggered grid
Coupling algorithm Fractional step method
Time advancement
Conductive term Crank–Nicolson method
Other terms Adams–Bashforth method
Spatial scheme 2nd-order central difference
Computational volume 4.8δ ×2δ ×3.2δ
Grid points 192×(96+36 or 18)×96
(x ×y (rib outside+rib inside)×z)
Grid resolution x
∗
=3.75
y
∗
=0.30∼6.50
z
∗
=5.0
the second-orderAdams–Bashforth and Crank–Nicolson schemes are used for the
nonlinear and viscous terms, respectively (see Section 4.1).
8.5 DNS of Turbulent heatTransfer in Channel Flow with
Transverse-Rib Roughness: Finite-Difference Method
DNS of turbulent heat transfer in channel flow with transverse-rib roughness was
carried out using the high-accuracy finite-difference method [13], in which flow
parameter and five types of wall roughness are arranged as listed inTable 8.3.The
number ofgrid points inthey-direction in theenclosureis 36 forCases1, b, and c,
and18 forCases2and3asindicatedinTable8.2.Accordingtothe classificationof
roughness [27, 28], Case 1 inTable 8.3 belongs to k-type roughness, and is similar
shape to the experimentofHanjali´c and Launder [29]. In Case 2, the ribs are set to
halftheheight ofCase1, andinCase3, theheightissettohalftheheight ofCase2.
In the k-type roughness, the effect of the roughness is expressed in terms of the
roughness Reynolds number, H
+
=u
τ
H/ν. In Cases b and c, the height of the ribs
is set the same as in Case 1, though the spacing of the ribs is varied systematically.
Case c belongsto d-type roughness, in whichthe effectof the roughness cannotbe
expressedbyH
+
. Ontheother hand,Case bisnot regardedasthe exact d-type, but
d-like type roughness. Note that the two kinds of roughness are extreme versions
and intermediate forms can exist [28].
8.5.1 Heat transfer and skin friction coefficients
Figures 8.3 and 8.4, respectively, show the skin friction coefficient and the Nusselt
number against the Reynolds number. By taking into account the asymmetr y [30]
Sunden CH008.tex 10/9/2010 15: 19 Page 282
282 Computational Fluid Dynamics and Heat Transfer
Table 8.3. Flow and rib parameters
Re
τ
150
Pr 0.71
H W S Roughness type
Case 1 0.2δ 0.2δ 0.6δ
Case 2 0.1δ 0.2δ 0.6δ k type
Case 3 0.05δ 0.2δ 0.6δ
Case b 0.2δ 0.4δ 0.4δ d-like type
Case c 0.2δ 0.2δ 0.2δ
10
3
0.01
0.05
C
fr,
C
fs
C
f
= 12Re
m
−1
C
f
= 0.073Re
m
−1/4
: Dean (1978)
10
4
Re
m
Case 1
Smooth
Case 2
Case 3
Case b
Case c
Plane channel
Rough
Figure 8.3. Distributions of skin friction coefficients.
2 × 10
3
10
10
4
50
Re
dh
N
U
= 0.021Pr
0.5
Re
dh
0.8
Case 1
Rough Smooth
Case 2
Case 3
Case b
Case c
Plane channel
: Kays & Crawford (1993)
Nu
r
, Nu
s
Figure 8.4. Distributions of Nusselt numbers.

Sunden CH008.tex 10/9/2010 15: 19 Page 283
Recent developments in DNS 283
in the flow field disturbed by the ribs, the skin friction coefficient and the Nusselt
number at the rough wall are defined as follows:
C
f
r
=
2
τ
wr
ρU
2
r
, Nu
r
=
2
q
wr
d
(T
h
−T
r
)λ
(13)
where d indicates the distance between the wall and the location where the mean
velocity becomes maximum, and denotes the bulk mean over the distance d.At
the smooth wall, they are similarly defined as follows:
C
fs
=
2τ
ws
ρU
2
s
, Nu
s
=
2q
ws
(2δ −d)
(T
s
− T
c
)λ
(14)
The wall shear stress, τ
ws
, at the (upper) smooth wall is estimated directly by
the mean velocity gradient on the wall and then,
τ
w
r
at the (lower) rough wall is
calculated from the balance of the imposed pressure gradient:
τ
w
r
=−2δ
d
p
dx
− τ
ws
= 2τ
w0
− τ
ws
(15)
Theabove-defined wallshearstressat therough wall,
τ
wr
, includesthe pressure
drag (form drag) as well as the viscous drag:
τ
w
r
= τ
wp
+ τ
wv
(16)
On the otherhand, because the fullydevelopedstate is assumed for the thermal
condition in the present study, there is no increase in the enthalpy of the flowing
fluidinthestreamwisedirection.Thus, theoverallheatfluxattheroughwall,
q
wr
,is
equal to the absolute value of that at the smooth wall, q
ws
, which can be estimated
directly by the mean temperature gradient on the wall. In order to compare the
results with the correlation curve by Kays and Crawford [31] for the pipe flow, the
length scales of the Reynolds and Nusselt numbers are doubled in Figure 8.3. In
those figures, the DNS results in the plane channel flow (Re
τ
=150) calculated by
thespectralmethod[16] arealsoincludedtocomparewiththe resultsofthepresent
DNS using the high-accuracy finite-difference method.
FromFigures8.3 and8.4, itcan beseen thatthe skinfriction coefficient andthe
Nusselt number at the rough wall become very large in comparison with those at
the corresponding smooth wall, where these quantities are well represented by the
correlation curves. Moreover, from Figure 8.3, even though the imposed pressure
gradient isthesameasin thesmoothwall, theribdecreases thebulkmeanvelocity,
so theReynoldsnumber heavilydepends on therib configuration; inCase 1, where
theribishighestinthek-typeroughnesswalls,theReynoldsnumberisthesmallest
among them. In the present study, Case 3 is found to be the lowest in drag. On
the other hand, in the d-like type roughness (Cases b and c), the heat transfer
augmentation is smallerthanthat in the k-type roughness with the same roughness
height (Case 1).

Sunden CH008.tex 10/9/2010 15: 19 Page 284
284 Computational Fluid Dynamics and Heat Transfer
Table 8.4. Coefficients for heat transfer rate at rough wall
(St
r
/C
f
r
)/(St
0
/C
f 0
) C
f
r
/C
f 0
Nu
r
/Nu
0
Case 1 0.61 3.93 2.41
Case 2 0.71 2.87 2.04
Case 3 0.85 1.66 1.42
Case b 0.69 2.44 1.67
Case c 0.69 2.10 1.46
Table8.4showstheStantonnumber,theskinfrictioncoefficient,andtheNusselt
number, whicharedividedbytheestimatedsmooth-wallvaluesfromthe respective
correlation curve [31, 32] for the same Reynolds number. In the k-type classifica-
tion, Case 1 enhances heat transfer most. However, from the viewpoint of the heat
transfercharacteristicincludingthedrag,ifwecomparetheStantonnumberdivided
by the skin friction coefficient
St
r
/C
f
r
, from Table 8.4, Case 1 enhances the heat
transfermorethanthesmoothwall, buttheoverallcharacteristicsofheattransferdo
not improvebecause of the large drag. However, Case 3, the k-type with thelowest
ribs, promotes the heat transfer with very low drag.This case is the most efficient
from the standpoint of overall heat transfer performance including the drag. In the
d-liketyperoughness,theheattransfercharacteristiccannotbeimprovedregardless
of the rib spacing.The stagnation region in the enclosure becomes larger than that
in the k-type roughness (not shown here), and the deterioration in heat transfer has
been profound there.Thus, in the following, we discuss the effects of the height of
therib onthe statisticalcharacteristics ofthermalproperty inthek-typeroughness,
which includes a rib configuration which promotes the heat transfer.
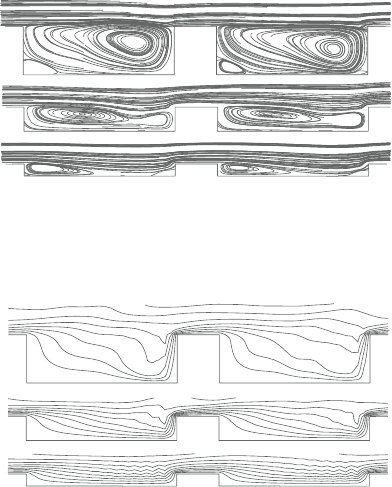
8.5.2 Velocity and thermal fields around the rib
Tovisualize thevelocityandthermalfields aroundtherib,Figures8.5and 8.6show
the mean streamlines estimated from the mean velocity profiles and contour lines
of the mean temperature distributions. The averages are taken only with respect
to the spanwise direction in these figures. Two-dimensional vortices exist in the
enclosures between the ribs in Cases 1 and 2, and their shapes are different in each
case. In Case 1, the center of the two-dimensional vortex is biased to the upstream
sideof therib andbecomesasymmetric, whereasin Case2, thecenter ofthevortex
is biased to the downstream side of the rib. Moreover, in Case 3, the small two-
dimensional vortices arelocated onboth sides ofthe rib, andthe flow reattachment
is seen in the enclosure.
On the other hand, from the contour lines of the mean temperature, around the
front corner of the rib, the spacing between the lines becomes smaller, making for
very active heat transfer there. In the enclosure between the ribs, the contour lines
are distorted corresponding to the streamlines and are not parallel to the bottom
wall. Especially, in Case 3, it is confirmed that the mean temperature contour lines
Sunden CH008.tex 10/9/2010 15: 19 Page 285
Recent developments in DNS 285
Case 1
Case 2
Case 3
Figure 8.5. Streamlines ofmeanvelocityaveraged inthe spanwisedirection. Flow
is left to right.
Case 1
Case 2
Case 3
Figure 8.6. Contour lines of mean temperature averaged in the spanwise direc-
tion.Theinterval between successive contourlevelis 0.02. Flow isleft
to right.
are densely distributed, causing moreenhanced heat transfer. On theupstreamside
of the ribs, the wavy patterns of temperature can be seen. This phenomenon is a
characteristic specific to a temperature field near the upstream side of the rib.
Figures 8.7 and 8.8 show the local skin friction coefficient, C
fr
(x)[=2τ
wv
(x)/
ρU
2
r
] and the local Nusselt number, Nu
r
(x)[=2q
wr
(x)d/(T
h
−T
r
)λ] along the
bottomoftheenclosureandthecrestontheroughwall, dividedbythevaluesonthe
smoothwall.Thesemean quantitiesareobtainedby averagingwith respectto time,
the spanwise direction and the streamwise period of the rib roughness. The local
wall shear stress, τ
wv
(x), and wall heat flux, q
wr
(x), are estimated directly from
the gradients of mean velocity and temperature, respectively. Thus, the local shear
stress shown in Figure 8.7 does not include the pressure drag see equation (16).
By averaging the local wall shear stress along the bottom of the enclosure and the
crest in the x-direction, the contributions of the viscous drag to the total drag of
the rough-wall side are estimated at 4.5%, 1.1% and, 20.8%, in Cases 1, 2, and 3,
respectively.AshrafianandAndersson [33]reported thecontribution ofthe viscous
drag to the total drag was 2.5%, in their DNS calculation of the rib-roughened
channel flow (the pitchto the height ratio, (S +W)/H,is8,Re
τ0
=400). Leonardi
et al. [34] have systematically investigated the effects of the pitch to the height
ratio on the contributions from the viscous and pressure drags. They reported that
