Amano R.S., Sunden B. (Eds.) Computational Fluid Dynamics and Heat Transfer: Emerging Topics
Подождите немного. Документ загружается.

Sunden CH008.tex 10/9/2010 15: 19 Page 296
296 Computational Fluid Dynamics and Heat Transfer
Table 8.5. Computational conditions
Re
τ
150
Pr 0.71
Case 1: Wall-normal rotation
WNR1 WNR2 WNR3 WNR4 WNR5
Ro
τ2
0.01 0.02 0.05 0.1 0.3
Case 2: Streamwise rotation
STR1 STR2 STR3 STR4 STR5
Ro
τ1
1.0 2.5 7.5 10.0 15.0
Case 3: Spanwise rotation
SPR1 SPR2 SPR3 SPR4 SPR5
Ro
τ3
0.0 0.75 1.5 3.0 5.0
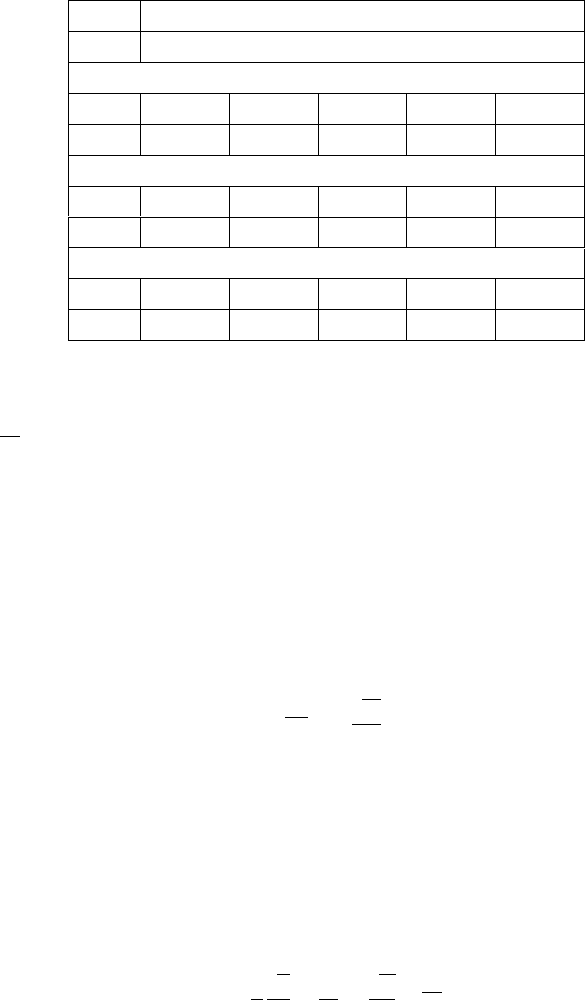
Therefore, to predict the flow of Case 1 exactly, the spanwise mean velocity
should be reproduced by a turbulence model. Note that the Reynolds shear stress,
uv, tends to decrease remarkably with the increase in rotational number as shown
in Figure 8.22b.
On the other hand, it is found from DNS that cases of streamwise rotating
channel flow (Case 2) involve the counter gradient turbulent diffusion in the span-
wise direction shown in Figure 8.23. In view of turbulence modeling, this fact
clearly demonstrates that the linear “eddy diffusivity turbulence model” (EDM)
and the quadratic “nonlinear eddy diffusivity turbulence model” (NLEDM) can-
not be applied to calculate the case of a streamwise rotating channel flow. Thus,
the following modeled equation 19 employed in the linear EDM and the quadratic
NLEDM cannot clearly express a counter gradient turbulent diffusion:
−
vw = ν
t
∂W
∂y
(19)
wheretheReynoldsshearstressesofaquadraticNLEDMareexpressedidenticalto
a linear model. Also, noted that the rotational term does not appear in the momen-
tum equation of a fully developed streamwise rotating channel flow indicated as
equation (22), in which the rotational effect is included implicitly in the Reynolds
shear stress in the same manner as the spanwise rotational flow [38]. Therefore, a
cubic NLEDM or Reynolds stress equation model (RSM) should be used for the
calculation of streamwise rotating channel flows as follows:
0 =−
1
ρ
∂
P
∂x
+
∂
∂y
ν
∂
U
∂y
−
uv
(20)

Sunden CH008.tex 10/9/2010 15: 19 Page 297
Recent developments in DNS 297
(a) (b)
(c) (d)
(e)
20
y/δ
U
+
w
+
uw
+
uv
+
10
0
−1
−0.4
−0.2
1
012
y/δ
012
y/δ
0
10
5
15
0.2
0
0.4
3
4
1
2
12
y/δ
012
y/δ
012
R
oτ
= 0.01
R
oτ
= 0.10
R
oτ
= 0.15
R
oτ
= 0.10
R
oτ
= 0.15
R
oτ
= 0.02
R
oτ
= 0.04
R
oτ
= 0.01
R
oτ
= 0.10
R
oτ
= 0.15
R
oτ
= 0.02
R
oτ
= 0.04
R
oτ
= 0.01
R
oτ
= 0.02
R
oτ
= 0.04
R
oτ
= 0.10
R
oτ
= 0.15
R
oτ
= 0.01
R
oτ
= 0.02
R
oτ
= 0.04
R
oτ
= 0.10
R
oτ
= 0.15
R
oτ
= 0.01
R
oτ
= 0.02
R
oτ
= 0.04
k
Figure 8.22. DNS results of wall-normal rotating flows (Case 1): (a) streamwise
mean velocities, (b) Reynolds shear stresses,
uv, (c) spanwise mean
velocities, (d) Reynolds shear stresses,
vw, and (e) turbulent kinetic
energy.
0 =−
1
ρ
∂
P
∂y
−
∂
v
2
∂y
+ 2
W (21)
0 =
∂
∂y
ν
∂
W
∂y
−
vw
(22)
As previouslystated, one of themain objectives in conductingDNSis to obtain
the detailed data for the evaluation of the turbulence models. Thus, this section
Sunden CH008.tex 10/9/2010 15: 19 Page 298
298 Computational Fluid Dynamics and Heat Transfer
20
10
01
(a)
2
1
0
0.3
0.2
0.1
0
01
(d)
01
(b)
2
−1
1
0
−1
U
+
W
+
k
+
uv
+
uw
+
Ro
τ
=1.0
Ro
τ
=2.5
Ro
τ
=7.5
Ro
τ
=10
Ro
τ
=15
Ro
τ
=1.0
Ro
τ
=2.5
Ro
τ
=7.5
Ro
τ
=10
Ro
τ
=15
Ro
τ
=1.0
Ro
τ
=2.5
Ro
τ
=7.5
Ro
τ
=10
Ro
τ
=15
Ro
τ
=1.0
Ro
τ
=2.5
Ro
τ
=7.5
Ro
τ
=10
Ro
τ
=15
Ro
τ
=1.0
Ro
τ
=2.5
Ro
τ
=7.5
Ro
τ
=10
Ro
τ
=15
y /δ
0
1
(c)
1
2
3
01
(e)
2
4
2
2
y /δ
y /δ
y /δ
y /δ
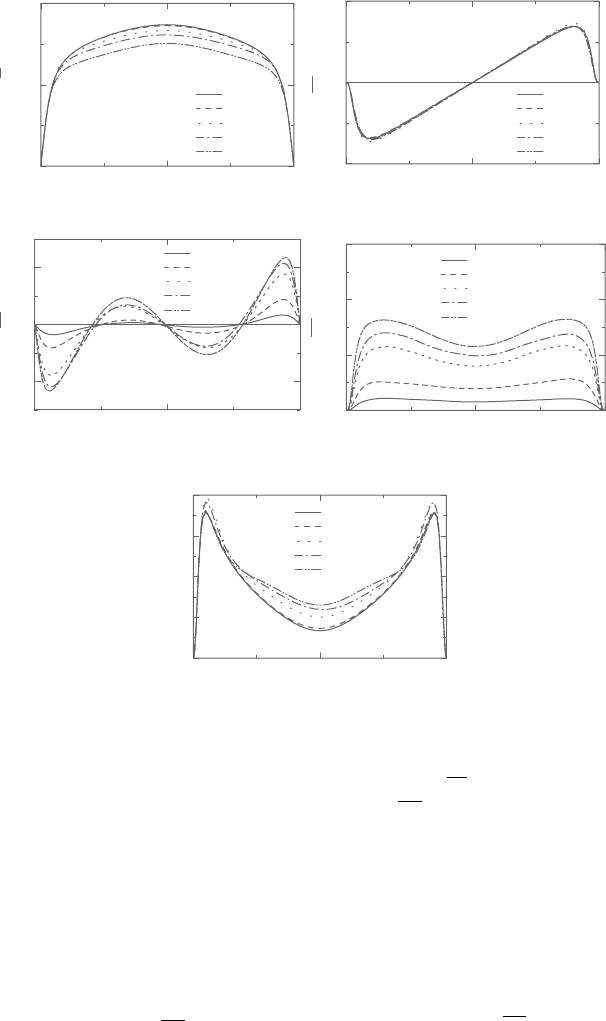
Figure 8.23. DNS results of streamwise rotating flows (Case 2): (a) streamwise
mean velocities, (b) Reynolds shear stresses,
uv, (c) spanwise mean
velocities, (d) Reynolds shear stresses,
vw, and (e) turbulent kinetic
energy.
briefly explains the characteristics of channel flows with heat transfer, and with
wall-normal or streamwise rotation [39]. DNSs of fully developed nonisothermal
channelflowswithwall-normal(Case1)orstreamwise(Case2)rotationarecarried
out for the 10 cases indicated inTable 8.5. DNS results are shown in Figures 8.24–
8.27.Inthesecases,thespanwisemeanvelocityappearstobecausedbyarotational
effect, which increases with the increase in rotation number in both cases. Also,
Reynolds shear stress,
vw, and the spanwise turbulent heat flux, wθ, are yielded
in both velocity and thermal fields as indicated in Figures 8.25 and 8.27 (note that
Sunden CH008.tex 10/9/2010 15: 19 Page 299
Recent developments in DNS 299
0.8
50
40
30
20
10
0
0.6
0.4
0.2
012
12
y/δ y/δ
Ro
τ
= 0.01
Ro
τ
= 0.02
Ro
τ
= 0.15
Ro
τ
= 0.10
Ro
τ
= 0.04
Ro
τ
= 0.01
Ro
τ
= 0.02
Ro
τ
= 0.15
Ro
τ
= 0.10
Ro
τ
= 0.04
kθ
+
(Θ − Θ
H
)/∆Θ
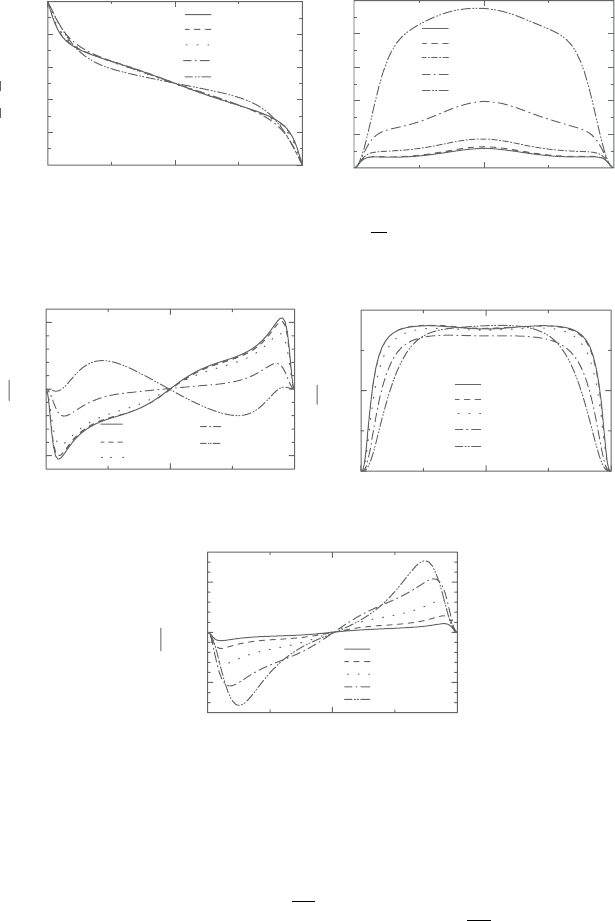
Figure 8.24. Distributions of mean temperature and temperature fluctuation k
θ
(Case 1).
(a) (b)
(c)
RO
τ
= 0.01
RO
τ
= 0.10
RO
τ
= 0.15
−5
5
0
−5
5
0
012
0.5
vθ
+
vθ
+
1
vθ
+
y/δ
012
y/δ
012
y/δ
RO
τ
= 0.02
RO
τ
= 0.04
RO
τ
= 0.01
RO
τ
= 0.02
RO
τ
= 0.04
RO
τ
= 0.10
RO
τ
= 0.15
RO
τ
= 0.01
RO
τ
= 0.02
RO
τ
= 0.04
RO
τ
= 0.10
RO
τ
= 0.15
Figure 8.25. Turbulent heat fluxes (Case 1): (a) streamwise, (b) wall-normal,
(c) spanwise.
turbulentquantitiesofvelocityfieldareomittedhere;fordetails, seeRef.[18]).Itis
well knownthat Reynoldsshearstress,
vw, remarkably relatesto thedistribution of
spanwisemean velocity,but thespanwiseturbulent heatflux,
wθ, hardlyaffectsthe
distribution of mean temperature due to the absence of mean temperature gradient
in the spanwise direction.
In Case 1, it can be seen that the profiles of mean temperature scarcely vary,
but the temperature fluctuations increase distinctly with the increase in rotation
number.As for the turbulent heat fluxes, decrease of the streamwise turbulent heat
Sunden CH008.tex 10/9/2010 15: 19 Page 300
300 Computational Fluid Dynamics and Heat Transfer
01
y/δ
2
0.2
0.4
0.6
0.8
1
R
oτ
= 10
R
oτ
= 15
R
oτ
= 1.0
R
oτ
= 2.5
R
oτ
= 7.5
01
y/δ
2
1
2
3
4
5
6
R
oτ
= 10
R
oτ
= 15
R
oτ
= 1.0
R
oτ
= 2.5
R
oτ
= 7.5
k
θ
+
(Θ − Θ
H
)∆Θ
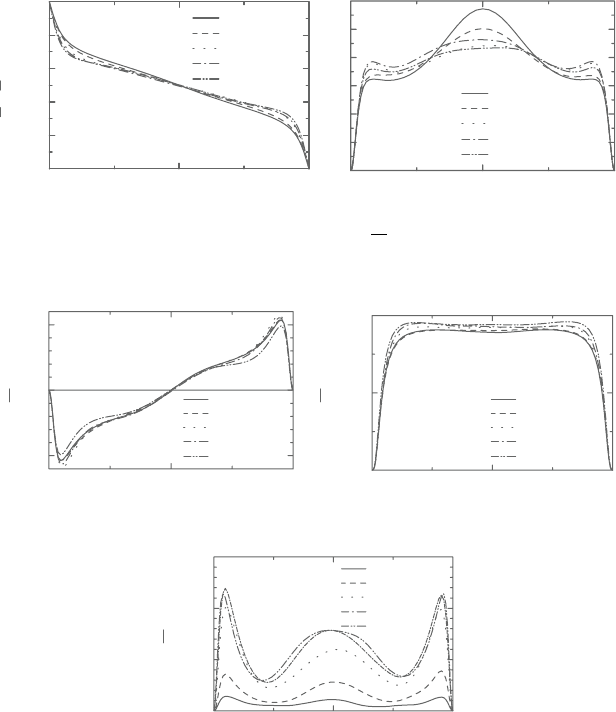
Figure 8.26. Distributions of mean temperature and temperature fluctuation k
θ
(Case 2).
R
oτ
= 10
R
oτ
= 15
R
oτ
= 1.0
R
oτ
= 2.5
R
oτ
= 7.5
1
0.5
1.5
01
y/δ
2
(c)
0.5
012
5
y/δ
R
oτ
= 10
R
oτ
= 15
R
oτ
= 1.0
R
oτ
= 2.5
R
oτ
= 7.5
0
−5
0
5
1
y/δ
2
R
oτ
= 10
R
oτ
= 15
R
oτ
= 1.0
R
oτ
= 2.5
R
oτ
= 7.5
uu
+
uu
+
uu
+
(a) (b)
Figure 8.27. Turbulent heat fluxes (Case 2): (a) streamwise, (b) wall-normal,
(c) spanwise.
flux, andincreaseinthespanwise turbulentheatfluxwithlargerotationnumberare
observed as shown in Figure 8.25. The streamwise turbulent heat flux ultimately
indicatesan inversesignat thelargestrotation number.On theother hand, thewall-
normal turbulent heat flux, which affects mean temperature distribution is kept in
the region of the channel center, while the decrease is found near the wall with the
increase in rotation number.
As for Case 2, since the streamwise mean velocity decreases little and the
spanwise mean velocity fluctuates significantly and increases with the increase in

Sunden CH008.tex 10/9/2010 15: 19 Page 301
Recent developments in DNS 301
rotationnumber[18], remarkable increasesin thespanwise turbulentheatflux, wθ,
are also observed near the wall and center of the channel. However, the mean tem-
perature and the other turbulent heat fluxes of this case are hardly affected by the
rotation as indicated in Figures 8.26 and 8.27. Note that the counter-gradient dif-
fusion phenomenon was found between the spanwise mean velocity and Reynolds
shear stress,
vw in Case 2[18].Therefore,thelinear eddy diffusivity model cannot
accurately predict in this case [18].
In view of turbulence modeling, this fact clearly demonstrates that the linear
eddy diffusivity models cannot be applied to calculate the thermal field of rotating
channelflow, because itis difficult toinclude therotational effect inthe lineareddy
diffusivity model. On the other hand, it is well known that it is difficult for a linear
eddy diffusivity model to predict the streamwise turbulent heat flux. Although the
spanwise heat flux also appears in these cases, the model might not predict it by
reason of the modeled hypothesis, i.e., gradient diffusion modeling. Therefore, in
order to accurately predict the heat transfer of rotating channel flows, the turbulent
heat-flux equation model, the algebraic turbulent heat-flux model, or the nonlinear
eddy diffusivity model should be used. In this study, the nonlinear eddy diffusivity
for heat model (NLEDHM) [16] is developed to predict adequately these heat
transfer phenomena of rotating channel flows.
8.7 Nonlinear Eddy Diffusivity Model forWall-Bounded
Turbulent Flow
8.7.1 Evaluations of existing turbulence models in rotating
wall-bounded flows
The evaluated models are acubicmodel by Craft et al.[40] (hereinafter referred to
as NLCLS) and a quadratic model by Nagano and Hattori [38] (NLHN).
Evaluations of wall-normal rotating flows predicted by the NLCLS and the
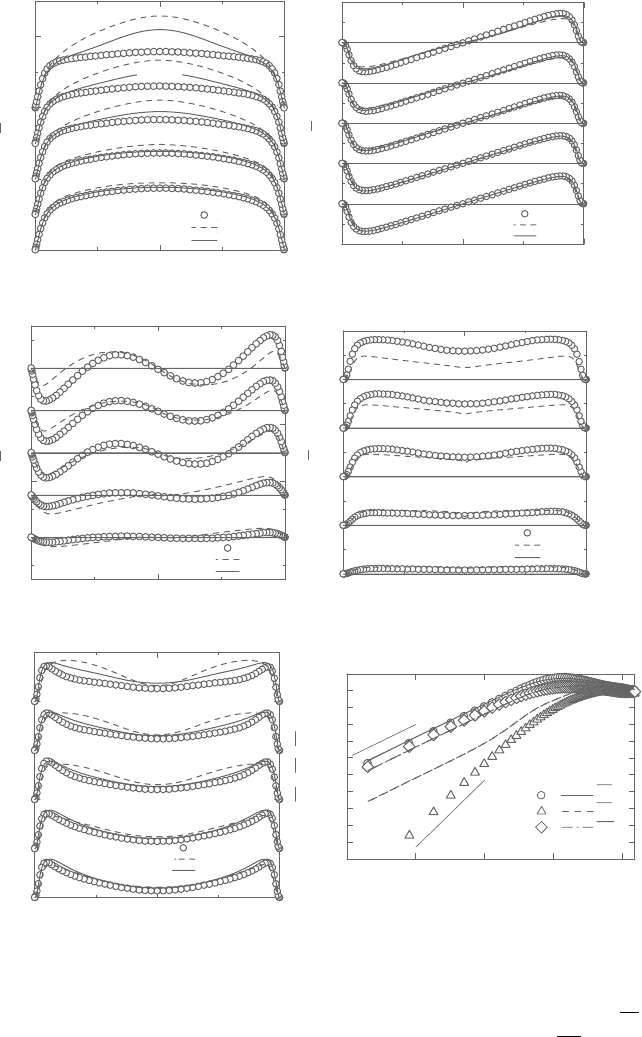
NLHN models are indicated in Figure 8.28. In this case, it can be seen that
the NLHN accurately reproduces turbulent quantities. Thus, one may consider
that streamwise rotating flows can be predicted using a quadratic nonlinear
model. However, the wall-limiting behavior of the Reynolds stress component
in the wall-normal direction is not predicted in the vicinity of the wall shown in
Figure 8.28f.
Figure8.29showsthe assessmentresultusingthepresent DNSof two-equation
modelswithNLEDMinthecaseofstreamwiserotatingchannelflow.Obviously,the
quadratic model cannot reproduce this flow as mentioned in the previous section.
The cubic model indicates overprediction of mean streamwise velocity,
U, and
underpredictstheReynoldsshearstress,
vw, inthecaseofahigherrotationnumber.
Thewall-limitingbehaviorofReynoldsstresscomponentsisshowninFigure8.29f.
Although theNLHN modelis modeled tosatisfy thewall-limitingbehaviourof the
Reynoldsstresscomponentinthewall-normaldirectioninspanwiserotationalflow,
it can be seen that the model does not reproduce the wall-limiting behavior.

Sunden CH008.tex 10/9/2010 15: 19 Page 302
302 Computational Fluid Dynamics and Heat Transfer
Ro
τ
=
0.15
Ro
τ
=
0.10
Ro
τ
=
0.04
Ro
τ
=
0.02
Ro
τ
=
0.01
DNS
10
0
U
+
0
0
0
01
(a)
2
y/δ
NLCLS
NLHN
Ro
τ
=
0.15
Ro
τ
=
0.10
Ro
τ
=
0.04
Ro
τ
=
0.02
Ro
τ
=
0.01
20
10
W
+
0
0
0
0
012
(c)
y/δ
DNS
NLCLS
NLHN
Ro
τ
=
0.15
Ro
τ
=
0.10
Ro
τ
=
0.04
Ro
τ
=
0.02
Ro
τ
=
0.01
5
0
K
+
0
0
0
0
(f)
01 2
y/δ
DNS
NLCLS
NLHN
Ro
τ
=
0.15
Ro
τ
=
0.10
Ro
τ
=
0.04
Ro
τ
=
0.02
Ro
τ
=
0.01
uv
+
0.5
0
0
0
0
0
−0.5
(d)
012
y/δ
DNS
NLCLS
NLHN
Ro
τ
=
0.15
Ro
τ
=
0.10
Ro
τ
=
0.04
Ro
τ
=
0.02
Ro
τ
=
0.01
1
0
uv
+
0
0
0
0
−1
(b)
012
y/δ
DNS
NLCLS
NLHN
Lines: NLHN
u
2
+
v
2
+
w
2
+
Ro
τ
=
0.1
(g)
Symbols: DNS
10
−2
10
−0
10
−2
10
−4
10
−6
10
−8
10
−10
10
−12
10
−14
10
−1
10
0
10
1
y
+
10
2
u
2
+
v
2
+
w
2
+
,,
Figure 8.28. Evaluations of predicted wall-normal rotating flows (Case 1):
(a) streamwise mean velocities, (b) Reynolds shear stresses,
uv,
(c)spanwise meanvelocities,(d) Reynoldsshearstresses,
vw, (e) tur-
bulentkineticenergy,and(f)wall-limitingbehaviorofReynoldsstress
components.
Sunden CH008.tex 10/9/2010 15: 19 Page 303
Recent developments in DNS 303
Roτ = 15
Roτ = 7.5
Roτ = 2.5
Roτ = 1.0
30
20
10
0
0
0
0
0
U
+
DNS
NLCLS
NLHN
y/δ
12
Roτ = 10
(a)
Roτ = 15
Roτ = 10
Roτ = 7.5
Roτ = 2.5
Roτ = 1.0
0
0
0
0
0
uv
+
DNS
NLCLS
NLHN
y/δ
0
12
1
−1
(b)
y/δ
(c)
y/δ
(d)
y/δ
(e)
(f)
W
+
k
+
DNS
NLCLS
NLHN
Roτ = 15
Roτ = 7.5
Roτ = 2.5
Roτ = 1.0
Roτ = 10
1.5
0
0
0
0
0
−0.5
102
DNS
NLCLS
NLHN
Roτ = 15
Roτ = 7.5
Roτ = 2.5
Roτ = 1.0
Roτ = 10
0
5
0
0
0
102
uw
+
DNS
NLCLS
NLHN
Roτ = 15
Roτ = 7.5
Roτ = 2.5
Roτ = 1.0
Roτ = 10
0
0.2
0
0
0
0
12
y
+
10
0
10
−2
10
−4
10
−6
10
−8
10
−10
10
−2
10
−1
10
−0
10
−1
10
−2
u
2
+
v
2
+
w
2
+
,,
Lines: NLHN
u
2
+
v
2
+
w
2
+
Ro
τ
=
0.1
Symbols: DNS
Figure 8.29. Evaluations of predicted streamwise rotating flows (Case 2):
(a) streamwise mean velocities, (b) Reynolds shear stresses,
uv,
(c)spanwise meanvelocities,(d) Reynoldsshearstresses,
vw, (e) tur-
bulentkineticenergy,and(f)wall-limitingbehaviorofReynoldsstress
components.
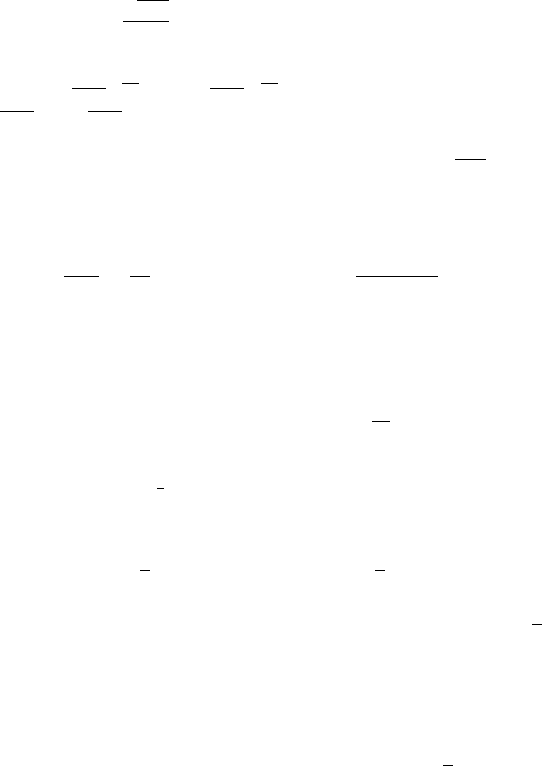
Sunden CH008.tex 10/9/2010 15: 19 Page 304
304 Computational Fluid Dynamics and Heat Transfer
8.7.2 Proposal of nonlinear eddy diffusivity model for wall-bounded flow
Fromtheseresults,weproposeacubicNLEDMinatwo-equationturbulencemodel
which can adequately predict rotational channel flows with arbitrary rotating axes,
in which a modeling of wall-limiting behavior of Reynolds stress components is
also considered.
The transport equation of Reynolds stress with the Coriolis term is given as
follows:
D
u
i
u
j
Dt
= D
ij
+ T
ij
+ P
ij
+ C
ij
+
ij
− ε
ij
(23)
where D
ij
is a molecular diffusion term, T
ij
is a turbulent and pressure diffusion
term, P
ij
=−u
i
u
k
(∂U
j
/∂x
k
)−u
j
u
k
(∂U
i
/∂x
k
) is a production term, C
ij
=−2
m
(!
mkj
u
i
u
k
+!
mki
u
j
u
k
) is a Coriolis term,
ij
is a pressure–stain correlation term
and ε
ij
is a dissipation term, respectively.
Introducing the Reynolds stress anisotropy tensor b
ij
=u
i
u
j
/2k −δ
ij
/3 and
neglecting the diffusive effect, the following relation is derived from equations (9)
and (23):
Db
ij
Dt
=
1
2k
(P
ij
+ C
ij
+
ij
− ε
ij
) −
b
ij
+ δ
ij
/3
k
(
P
k
− ε
)
(24)
Inthelocalequilibriumstate,sincetherelationDb
ij
/Dt =0holds,equation(24)
yields the following relation:
(P
ij
+ C
ij
+
ij
− ε
ij
) = 2
b
ij
+
δ
ij
3
(
P
k
− ε
)
(25)
Using theform ε
ij
=
2
3
εδ
ij
+
D
ε
ij
of thedissipation term [41] forequation (25),
we can obtain:
(P
k
− ε)b
ij
=−
2
3
kS
ij
− k
b
ik
S
jk
+ b
jk
S
ik
−
2
3
b
mn
S
mn
δ
ij
(26)
− k[b
ik
(W
jk
+ 2ε
mkj
m
) +b
jk
(W
ik
+ 2ε
mki
m
)] +
1
2
ij
where
ij
=
ij
−
D
ε
ij
, and the modeled
ij
is employed as the following general
linear model:
ij
=−C
1
εb
ij
+ C
2
kS
ij
+ C
3
k
b
ik
S
jk
+ b
jk
S
ik
−
2
3
b
mn
S
mn
δ
ij
(27)
+ C
4
k(b
ik
W
jk
+ b
jk
W
ik
)
where C
1
∼C
5
are model constants.

Sunden CH008.tex 10/9/2010 15: 19 Page 305
Recent developments in DNS 305
Substitutingequation(27)into(26)andintroducingnondimensionalquantities,
we can obtain the following relation:
b
∗
ij
=−S
∗
ij
−
b
∗
ik
S
∗
jk
+ b
∗
jk
S
∗
ik
−
2
3
b
∗
k
S
∗
k
δ
ij
+ b
∗
ik
W
∗
kj
+ b
∗
jk
W
∗
ki
(28)
where
S
∗
ij
=
1
2
gτ(2 − C
3
)S
ij
, W
∗
ij
=
1
2
gτ(2 − C
4
)
ij
+
C
4
− 4
C
4
− 2
ε
mji
m
b
∗
ij
=
C
3
− 2
C
2
−
4
3
b
ij
, τ =
k
ε
, g =
1
2
C
1
+
P
k
ε
+
G
k
ε
− 1
−1
⎫
⎪
⎪
⎪
⎬
⎪
⎪
⎪
⎭
(29)
Equation (28) can be written in the matrix form as:
b
∗
=−S
∗
−
b
∗
S
∗
+ S
∗
b
∗
−
2
3
{b
∗
S
∗
}I
+ b
∗
W
∗
− W
∗
b
∗
(30)
In order to derive an explicitform of b
∗
from equation (30), the integrity basis,
b
∗
=
λ
Q
(λ)
T
(λ)
first proposed by Pope [42], is used with the following 10 basis
tensors:
T
(1)
= S
∗
, T
(6)
= W
∗2
S
∗
+ S
∗
W
∗2
−
2
3
{S
∗
W
∗2
}I
T
(2)
= S
∗
W
∗
− W
∗
S
∗
, T
(7)
= W
∗
S
∗
W
∗2
− W
∗2
S
∗
W
∗
T
(3)
= S
∗2
−
1
3
{S
∗2
}I, T
(8)
= S
∗
W
∗
S
∗2
− S
∗2
W
∗
S
∗
T
(4)
= W
∗2
−
1
3
{W
∗2
}I, T
(9)
= W
∗2
S
∗2
+ S
∗2
W
∗2
−
2
3
{S
∗2
W
∗2
}I
T
(5)
= W
∗
S
∗2
− S
∗2
W
∗
, T
(10)
= W
∗
S
∗2
W
∗2
− W
∗2
S
∗2
W
∗
⎫
⎪
⎪
⎪
⎪
⎪
⎬
⎪
⎪
⎪
⎪
⎪
⎭
(31)
Substituting equation (31) into b
∗
=
λ
Q
(λ)
T
(λ)
gives:
b
∗
=Q
(1)
S
∗
+ Q
(2)
(S
∗
W
∗
− W
∗
S
∗
) +Q
(3)
S
∗2
−
1
3
{S
∗2
}I
+ Q
(4)
W
∗2
−
1
3
{W
∗2
}I
+ Q
(5)
(W
∗
S
∗2
− S
∗2
W
∗
)
+ Q
(6)
W
∗2
S
∗
+ S
∗
W
∗2
−
2
3
{S
∗
W
∗2
}I
(32)
+ Q
(7)
(W
∗
S
∗
W
∗2
− W
∗2
S
∗
W
∗
) +Q
(8)
(S
∗
W
∗
S
∗2
− S
∗2
W
∗
S
∗
)
+ Q
(9)
W
∗2
S
∗2
+ S
∗2
W
∗2
−
2
3
{S
∗2
W
∗2
}I
+ Q
(10)
(W
∗
S
∗2
W
∗2
− W
∗2
S
∗2
W
∗
)
