Alligood K., Sauer T., Yorke J.A. Chaos: An Introduction to Dynamical Systems
Подождите немного. Документ загружается.


4.5 FRACTAL D IMENSION
✎ E XERCISE T4.8
Show that the box-counting dimension of a disk (a circle together with its
interior) is 2.
Three simplifications will be introduced that make Definition 4.14 easier
to use. First, the limit as
⑀
→ 0 need only be checked at a discrete sequence of
box sizes, for example
⑀
⫽ 2
⫺n
or
⑀
⫽ n
⫺2
, n ⫽ 1, 2, 3,.... Second, the boxes
need not be cemented into a grid—they can be moved around to more easily fit
the set at hand. This approach may slightly decrease the number of boxes needed,
without changing the dimension. Third, boxes don’t need to be square boxes:
they could be spheres or tetrahedra, for example.
Simplification 1. It is sufficient to check
⑀
⫽ b
n
, where lim
n→
⬁
b
n
⫽ 0and
lim
n→
⬁
ln b
n⫹1
ln b
n
⫽ 1.
We begin by describing the first simplification for a set in ⺢
2
,andthen
generalize to ⺢
m
. For each
⑀
smaller than 1, there is some n ⱖ 0suchthat
⑀
lies between b
n⫹1
and b
n
. In ⺢
2
, any box of side b
n⫹1
is covered by 4 or fewer
boxes of the
⑀
-grid, as shown in Figure 4.14. It follows that if N(b
n⫹1
) boxes
of side-length b
n⫹1
cover a set S, then the number of
⑀
-boxes that will cover S
satisfies N(
⑀
) ⱕ 4N(b
n⫹1
). By the same token, any
⑀
-box is covered by 4 or fewer
boxes of the b
n
–grid, so N(b
n
) ⱕ 4N(
⑀
). Therefore we have the inequality
N(b
n
)
4
ⱕ N(
⑀
) ⱕ 4N(b
n⫹1
).
s
1
s
2
Figure 4.14 A box within a larger grid.
If s
1
⬍ s
2
, then four two-dimensional boxes of side s
2
are sufficient to cover a box of
side s
1
.In⺢
m
,2
m
boxes are sufficient. This fact is the key to Simplification 1.
175

F RACTALS
For the case of ⺢
m
, the 4 is replaced by 2
m
,sothat
2
⫺m
N(b
n
) ⱕ N(
⑀
) ⱕ 2
m
N(b
n⫹1
). (4.5)
It follows from b
n⫹1
ⱕ
⑀
⬍ b
n
that
⫺ ln b
n⫹1
ⱖ⫺ln
⑀
⬎⫺ln b
n
. (4.6)
Putting (4.5) and (4.6) together,
ln b
n
ln b
n⫹1
⫺m ln 2 ⫹ ln N (b
n
)
⫺ ln b
n
ⱕ
ln N(
⑀
)
ln(1
⑀
)
ⱕ
m ln 2 ⫹ ln N(b
n⫹1
)
⫺ ln b
n⫹1
ln b
n⫹1
ln b
n
. (4.7)
Thus, if lim
n→
⬁
ln N(b
n
)
ln(1 b
n
)
⫽ d, then the terms on the left and right tend to the limit
d as n →
⬁
, and likewise the middle term must approach d as
⑀
→ 0.
Theorem 4.15 Assume that b
1
⬎ b
2
⬎ ..., lim
n→
⬁
b
n
⫽ 0,andlim
n→
⬁
ln b
n⫹1
ln b
n
⫽ 1.If
lim
n→
⬁
ln N(b
n
)
ln(1 b
n
)
⫽ d,
then lim
⑀
→0
ln N(
⑀
)
ln(1
⑀
)
⫽ d, and therefore the box-counting dimension is d.
Simplification 2. Boxes can be moved to improve efficiency of the cover.
The second simplification refers to the fact that we could have alternatively
defined the box-counting dimension by replacing N(
⑀
), the number of grid boxes
hit by the set, with the smallest possible number N
0
(
⑀
)of
⑀
-boxes (not necessarily
from any particular grid) that cover the set S. The boxes must be translates of grid
boxes. In this formulation, rotations of the boxes are not allowed. We might be
able to cover S more efficiently this way—by nudging some of the grid boxes to
more convenient locations. Clearly N
0
(
⑀
)isatmostN(
⑀
), and could be less.
For all the simplicity of this alternate definition, it may be very difficult in
practice to determine N
0
(
⑀
). On the other hand, the calculation of N(
⑀
) is always
accessible—one can lay a grid over the set and count boxes (this assumes we have
complete knowledge of the set). As we show next, both definitions result in the
same box-counting dimension.
By definition, N
0
(
⑀
) ⱕ N(
⑀
). We also know, as above, that any
⑀
-box
whatsoever is covered by 2
m
or fewer
⑀
-grid-boxes, so that N(
⑀
) ⱕ 2
m
N
0
(
⑀
). The
176

4.6 COMPUTING THE B OX-COUNTING D IMENSION
string of inequalities
N
0
(
⑀
) ⱕ N(
⑀
) ⱕ 2
m
N
0
(
⑀
) (4.8)
shows as in (4.7) that the grid definition (using N(
⑀
)) and the gridless definition
(using N
0
(
⑀
)) are equivalent.
Simplification 3. Other sets can be used in place of boxes.
We could have defined N
0
(
⑀
) as the smallest number of
⑀
-disks (disks of
radius
⑀
)thatcoverthesetS. The reasoning above goes through with little change.
Other shapes, such as triangles or tetrahedra, could be used. We use triangles to
determine the dimension of the Sierpinski gasket below.
4.6 COMPUTING THE BOX-COUNTING
DIMENSION
We are now ready to compute the dimension of the middle-third Cantor set.
Recall that the Cantor set K is contained in K
n
, which consists of 2
n
intervals,
each of length 1 3
n
. Further, we know that K contains the endpoints of all 2
n
intervals, and that each pair of endpoints lie 3
⫺n
apart. Therefore the smallest
number of 3
⫺n
-boxes covering K is N
0
(3
⫺n
) ⫽ 2
n
. We compute the box-counting
dimension of K as
boxdim(K) ⫽ lim
n→
⬁
ln 2
n
ln 3
n
⫽ lim
n→
⬁
n ln 2
n ln 3
⫽
ln 2
ln 3
.
We can compute the dimension of the Sierpinski gasket by exploiting the
second and third simplifications above. We will use equilateral triangles of side-
length (1 2)
n
. After step n of the construction of Example 4.6, there remain 3
n
equilateral triangles of side 2
⫺n
. This is the smallest number of triangles of this size
that contains the completed fractal, since all edges of the removed triangles lie in
the fractal and must be covered. Therefore N
0
(2
⫺n
) ⫽ 3
n
, and the box-counting
dimension works out to ln 3 ln 2.
✎ E XERCISE T4.9
Find the box-counting dimension of the invariant set of the skinny baker
map of Example 4.5.
177
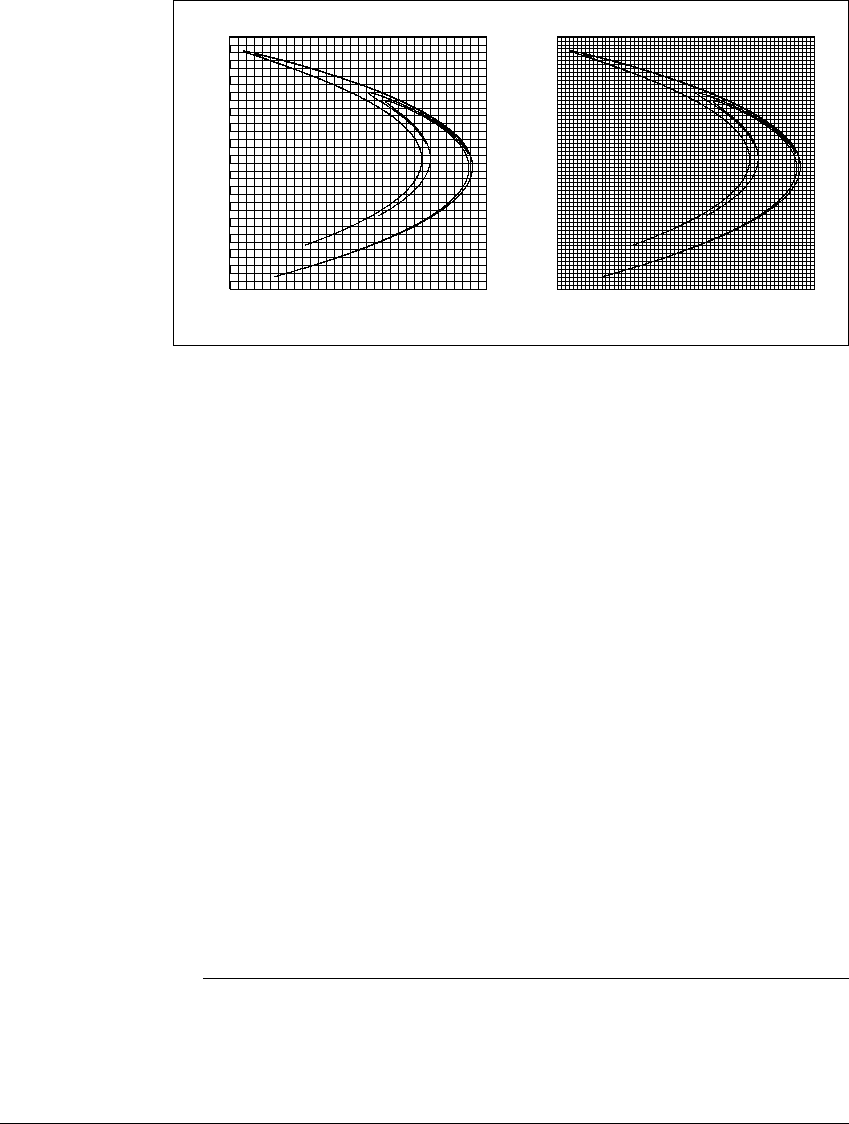
F RACTALS
-2
0
2
-2 0 2
-2
0
2
-2 0 2
Figure 4.15 Finding the box-counting dimension of the H
´
enon attractor.
Two grids are shown, with gridsize
⑀
⫽ 1 8and1 16 respectively.
For a more complicated example such as the H
´
enon attractor of Example
4.10, no exact formula can be found for the box-counting dimension. We are
stuck with drawing pictures and counting boxes, and using the results to form an
estimate of the dimension. In Figure 4.15, we extend the grid of Figure 4.13 to
smaller boxes. The side-length
⑀
of the boxes is 1 8and1 16, respectively, in
the two plots. A careful count reveals a total of 177 boxes hit by the attractor for
⑀
⫽ 1 8, 433 for
⑀
⫽ 1 16, 1037 for
⑀
⫽ 1 32, 2467 for
⑀
⫽ 1 64, and 5763 for
⑀
⫽ 1 128.
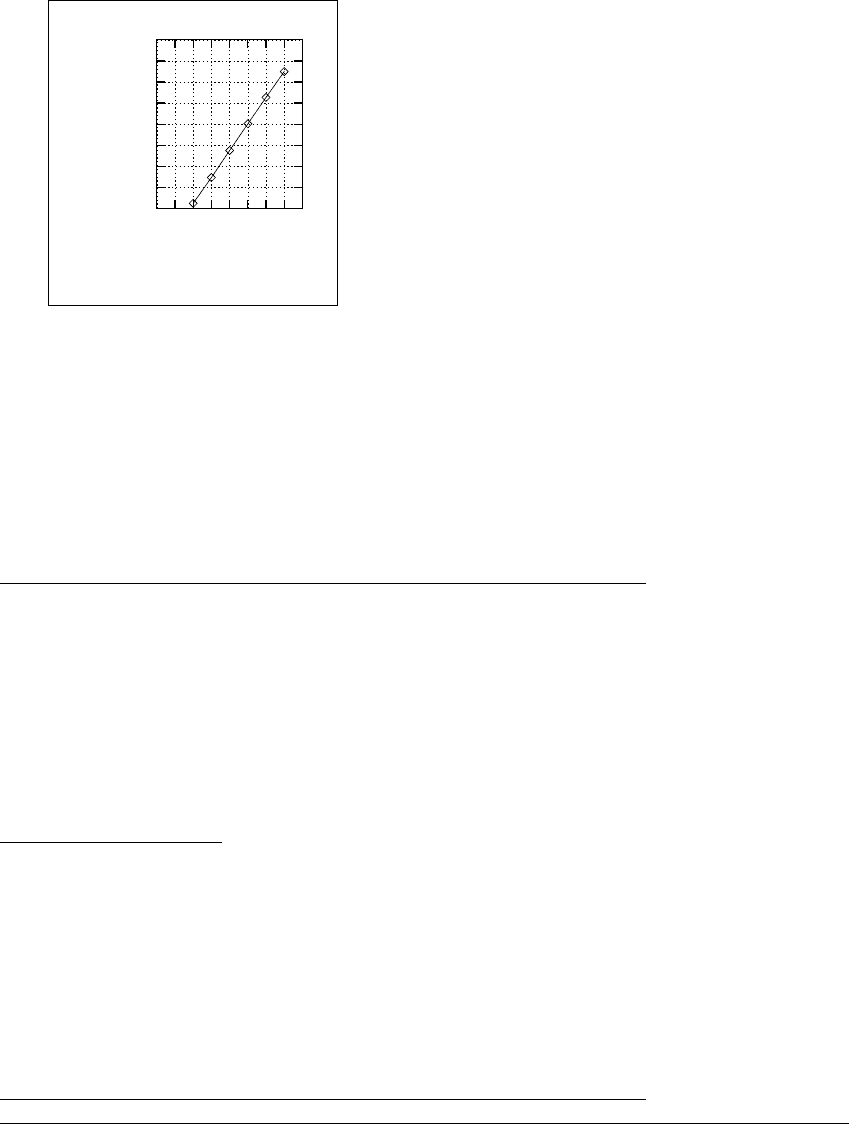
In Figure 4.16 we graph the results of the box count. We graph the quantity
log
2
N(
⑀
) versus log
2
(1
⑀
) because its ratio is the same as ln N(
⑀
) ln(1
⑀
), which
defines box-counting dimension in the limit as
⑀
→ 0. We used box sizes
⑀
⫽ 2
⫺2
through 2
⫺7
, and take log
2
of the box counts given above. The box-counting
dimension corresponds to the slope in the graph. Ideally, Figure 4.16 would be
extended as far as possible to the right, in order to make the best approximation
possible to the limit. The slope in the picture gives a value for the box-counting
dimension approximately equal to 1.27.
➮ COMPUTER EXPERIMENT 4.4
Write a program for calculating box-counting dimension of planar sets. Test
the program by applying it to a long trajectory of the iterated function system
178
4.6 COMPUTING THE B OX-COUNTING D IMENSION
6
8
10
12
14
0 2 4 6 8
log2(N(eps))
log2(1/eps)
Figure 4.16 Box-counting dimension of the H
´
enon attractor.
A graphical report of the results of the box counts in Figures 4.13 and 4.15. The box-
counting dimension is the limit of log
2
N(
⑀
) log
2
(1
⑀
). The dimension corresponds
to the limiting slope of the line shown, as
⑀
→ 0, which is toward the right in this
graph. The line shown has slope ⬇ 1.27.
for the Sierpinski gasket. To how many correct digits can you match the correct
value ln 3 ln 2?
In the remainder of this section we investigate whether there is a rela-
tionship between box-counting dimension and the property of measure zero. By
constructing a Cantor set with a different ratio of removed intervals—say, 1 2
instead of 1 3—we can find a measure-zero set that has a different box-counting
dimension. What about Cantor sets in the unit interval for which the lengths
of the removed intervals sum to a number less than one? Such sets, called “fat”
fractals, are not measure-zero sets.
✎ E XERCISE T4.10
Consider the Cantor set D formed by deleting the middle subinterval of
length 4
⫺k
from each remaining interval at step k. (a) Prove that the length
of D is 1 2. Thus D is a fat fractal. (b) What is the box–counting dimension
of D? (c) Let f be the function on [0, 1] which is equal to 1 on D and 0
elsewhere. It is the limit of functions that are Riemann integrable. Note
that f is not Riemann integrable. What is the value of any lower Riemann
sum for f ?
179

F RACTALS
Theorem 4.16 Let A be a bounded subset of ⺢
m
with boxdim(A) ⫽ d ⬍ m.
Then A is a measure zero set.
Proof: The set A is contained in the union of N (
⑀
) boxes of side
⑀
. Then
lim
⑀
→0
ln
⑀
m
N(
⑀
)
ln
⑀
⫽ lim
⑀
→0
m ln
⑀
⫹ ln N(
⑀
)
ln
⑀
⫽ m ⫺ d ⬎ 0.
Since ln
⑀
→ ⫺
⬁
, we conclude that ln
⑀
m
N(
⑀
) → ⫺
⬁
,sothat
⑀
m
N(
⑀
) → 0. We
have found
⑀
-boxes covering A whose total volume
⑀
m
N(
⑀
) is as small as desired.
This is the definition of measure zero.
The converse of Theorem 4.16 does not hold; there are subsets of the
unit interval (in fact, countable subsets) with box-counting dimension one and
measure zero.
✎ E XERCISE T4.11
(a) Find the box-counting dimension of the set of integers 兵0,...,100其.
(b) Find the box-counting dimension of the set of rational numbers in
[0, 1].
4.7 CORRELATION DIMENSION
Box-counting dimension is one of several definitions of fractal dimension that
have been proposed. They do not all give the same number. Some are easier to
compute than others. It is not easy to declare a single one to be the obvious choice
to characterize whatever fractal dimension means.
Correlation dimension is an alternate definition that is popular because
of its simplicity and lenient computer storage requirements. It is different from
box-counting dimension because it is defined for an orbit of a dynamical system,
not for a general set. More generally, it can be defined for an invariant measure,
which we describe in Chapter 6.
Let S ⫽ 兵 v
0
, v
1
,...其 be an orbit of the map f on ⺢
n
. For each r ⬎ 0, define
the correlation function C(r) to be the proportion of pairs of orbit points within
r units of one another. To be more precise, let S
N
denote the first N points of the
orbit S.Then
C(r) ⫽ lim
N→
⬁
#兵pairs 兵w
1
, w
2
其 : w
1
, w
2
in S
N
, |w
1
⫺ w
2
| ⬍ r其
#兵pairs 兵w
1
, w
2
其 : w
1
, w
2
in S
N
其
(4.9)
180
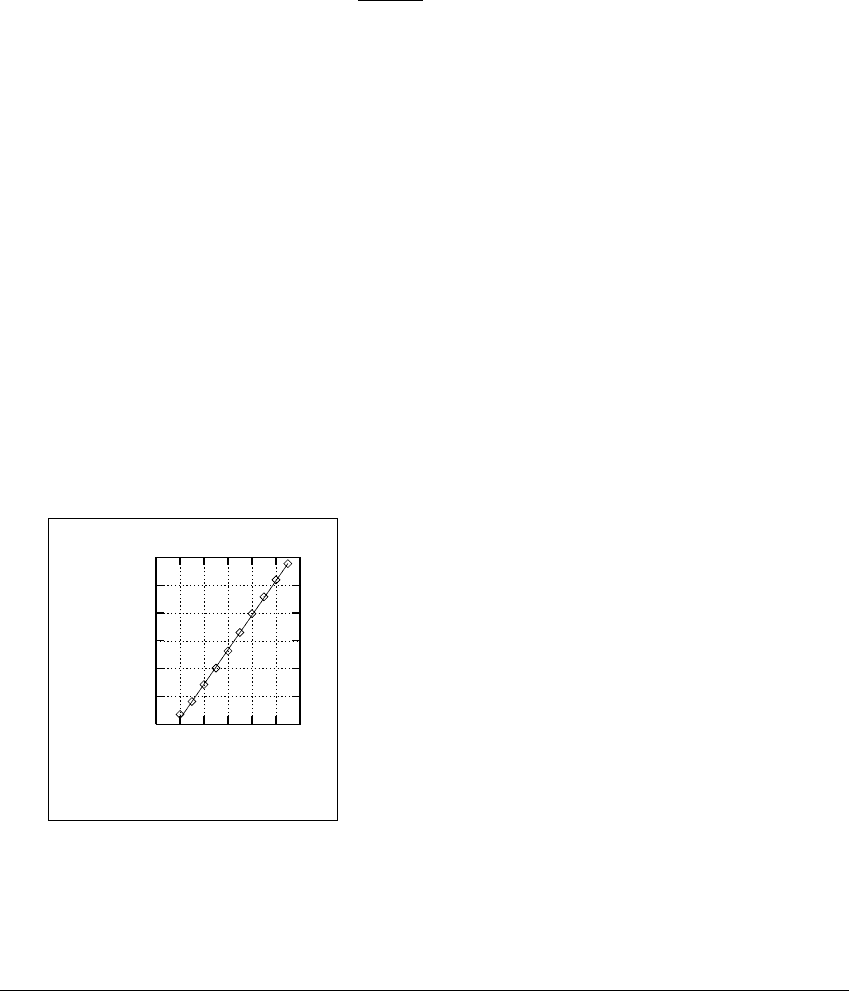
4.7 CORRELATION D IMENSION
The correlation function C(r) increases from 0 to 1 as r increases from 0 to
⬁
.If
C(r) ⬇ r
d
for small r, we say that the correlation dimension of the orbit S is d.
More precisely:
cordim(S) ⫽ lim
r→0
log C(r)
log(r)
, (4.10)
if the limit exists.
Figure 4.17 shows an attempt to measure the correlation dimension of the
orbit of the H
´
enon attractor shown in Figure 4.13. An orbit of length N ⫽ 1000
was generated, and of the (1000)(999) 2 possible pairs, the proportion that lie
within r was counted for r ⫽ 2
⫺2
,...,2
⫺8
. According to the definition (4.10),
we should graph log C(r) versus log r and try to estimate the slope as r → 0. This
estimate gives cordim(S) ⬇ 1.23 for the H
´
enon attractor, slightly less than the
box-counting dimension estimate.
For dimension measurements in high-dimensional spaces, correlation di-
mension can be quite practical when compared with counting boxes. The number
of
⑀
-boxes in the unit “cube” of ⺢
n
is
⑀
⫺n
.If
⑀
⫽ 0.01 and n ⫽ 10, there are poten-
tially 10
20
boxes that need to be tracked, leading to a significant data structures
problem. Because no boxes are necessary to compute correlation dimension, this
problem doesn’t arise.
-8
-6
-4
-2
-8 -6 -4 -2
log2(C(r))
log2(r)
Figure 4.17 Correlation dimension of the H
´
enon attractor.
A graphical report of the results of the correlation dimension estimate for the
H
´
enon attractor. The correlation dimension is the limit of log
2
C(r) log
2
(r). The
dimension corresponds to the limiting slope of the line shown, as r
→ 0, which is
toward the left. The line shown has slope ⬇ 1.23.
181

F RACTALS
The use of correlation dimension as a way to characterize chaotic attractors
was suggested by theoretical physicists (Grassberger and Procaccia, 1983). Since
then it has become a common tool for the analysis of reconstructed attractors
from experimental data, such as the example of Lab Visit 3. Lab Visit 4 shows two
illustrative applications of this method. More of the theory and practical issues
of correlation dimension and other dimensions can be found in (Ott, Sauer, and
Yorke, 1994).
182
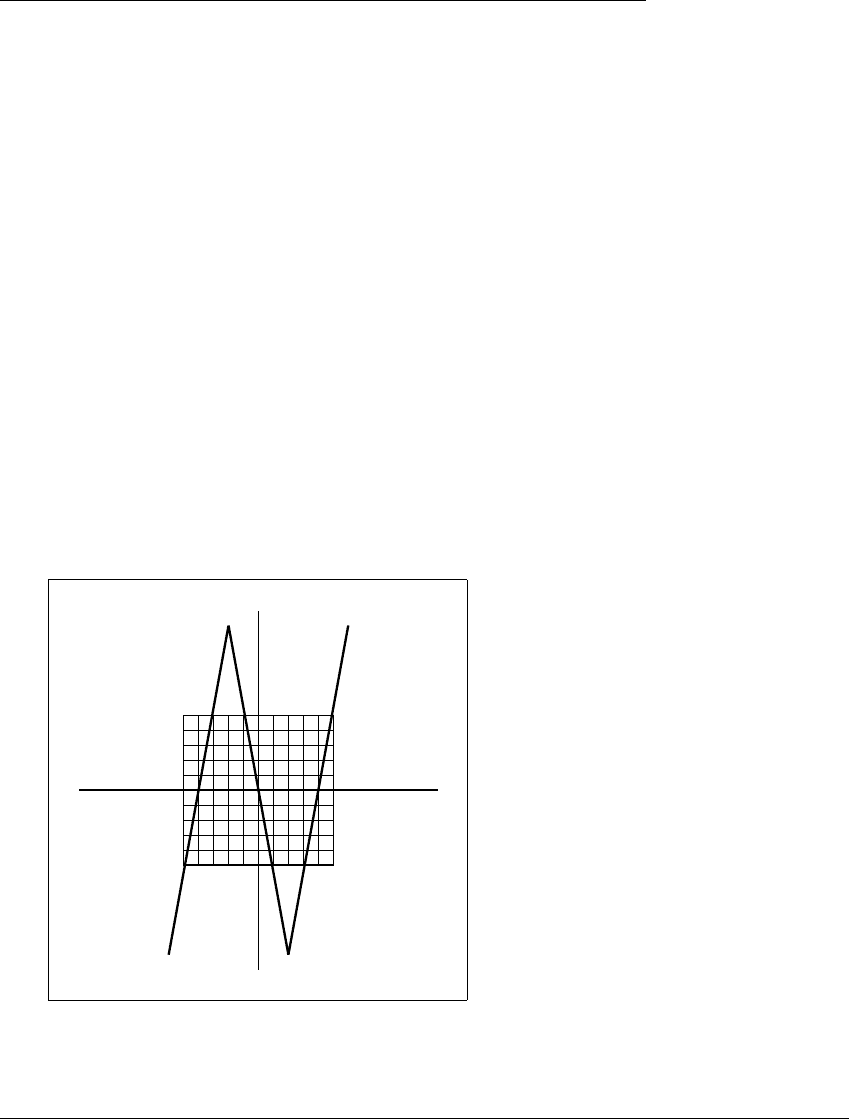
C HALLENGE 4
☞ C HALLENGE 4
Fractal Basin Boundaries and the
Uncertainty Exponent
W
HY IS THE fractal dimension of a set important? In a broad sense, of
course, it tells us something about the geometry of the set through its scaling
behavior. But how do we use such information? In this challenge, we explore
how the complexity of a fractal can influence final state determination within
a dynamical system and see what the dimension of the fractal says about the
resulting uncertainty.
Our model will be a one-dimensional, piecewise linear map F, which is
illustrated in Figure 4.18. Under this map, almost all initial conditions will have
orbits that tend to one or the other of two final states. Specifically, F is given by
the following formula:
F(x) ⫽
5x ⫹ 4ifx ⱕ⫺0.4
⫺5x if ⫺0.4 ⱕ x ⱕ 0.4
5x ⫺ 4ifx ⱖ 0.4
1
-1
-1
1
Figure 4.18 A piecewise linear map with fractal basin boundaries.
The orbits of almost every initial value tend to either ⫹
⬁
or ⫺
⬁
; the boundary
between the two basins is fractal.
183

F RACTALS
Notice that any initial condition x
0
⬎ 1 generates an orbit that tends to
⫹
⬁
. Similarly, the orbit of any x
0
⬍⫺1goesto⫺
⬁
. There are no fixed-point
sinks or periodic sinks. In fact, the orbits of most points, even those in the interval
[⫺1, 1], become unbounded under iteration by F. Normally, we group together
points whose orbits diverge to infinity (here either plus or minus infinity) and
call the set the “basin of infinity”. For the purposes of this challenge, however, we
distinguish points whose orbits go to ⫹
⬁
from those that go to ⫺
⬁
. Let B
⫹
⬁
be
the basin of ⫹
⬁
,letB
⫺
⬁
be the basin of ⫺
⬁
, and let J be the set of points whose
orbits stay in [⫺1, 1] for all iterates of F.
Step 1 Describe B
⫹
⬁
,B
⫺
⬁
, and J. [Hint: Start by dividing the interval
[⫺1, 1] into five equal parts and deciding where each part goes under the map.]
Step 2 Show: boxdim(J) ⫽
ln 3
ln 5
.
Step 3 Show that for every x in B
⫹
⬁
there exists
⑀
⬎ 0 such that the
epsilon neighborhood N
⑀
(x) 傺 B
⫹
⬁
. (The analogous statement for B
⫺
⬁
also
holds.) In other words, the basin is an open set.
Step 4 Show that the following characterization holds for each y in J: For
every
⑀
⬎ 0,N
⑀
(y) contains points of both B
⫹
⬁
and B
⫺
⬁
.
By definition, the orbit of an initial point x in B
⫹
⬁
or B
⫺
⬁
, will tend to ⫹
⬁
or ⫺
⬁
. If x is near a boundary point (a point in J), however, lack of measurement
accuracy can make final state prediction impossible. For example, if accuracy is
specified to within
⑀
⫽ 0.1, then there is no way to decide whether a point in the
intervals (⫺1, ⫺0.5), (⫺0.3, 0.3), or (0.5, 1.0) is in B
⫹
⬁
or B
⫺
⬁
. The problem
is that these points are all within 0.1 of a boundary point, and therefore all within
0.1 of points of both basins. Points within distance
⑀
⬎ 0 of a basin boundary
point are called
⑀
-uncertain points. The complete set of 0.1-uncertain points
between ⫺1and⫹1 is the union of the three above open intervals. The total
length of these intervals is 1.6, or 80% of the interval [⫺1, 1].
More generally, suppose that J is the fractal boundary of two basins in ⺢. In
Steps 5 and 6, show there exists a number p ⬎ 0, which depends on boxdim(J),
such that the total length of
⑀
-uncertain points (as
⑀
→ 0) is proportional to
⑀
p
.
The number p is called the uncertainty exponent.
Step 5 Let L(
⑀
) be the total length of
⑀
-uncertain points, and N(
⑀
)the
number of
⑀
-intervals needed to cover them. Show that
⑀
N(
⑀
) ⱕ L(
⑀
) ⱕ 3
⑀
N(
⑀
).
Step 6 Let p ⫽ 1⫺ boxdim(J). Show: lim
⑀
→0
(ln L(
⑀
)) (ln
⑀
) ⫽ p,ifthe
limit exists.
184
