Alligood K., Sauer T., Yorke J.A. Chaos: An Introduction to Dynamical Systems

Подождите немного. Документ загружается.

4.4 FRACTAL B ASIN B OUNDARIES

(a)

(b) (c)

Figure 4.8 Self-similarity of the H

enon basin.

The points in white are attracted to the period-two attractor 兵(1, 0.3), (0.3, 1)其

of (4.2), marked with crosses. The points in black are attracted to inﬁnity

with iteration. (a) The region [⫺2.5, 2.5] ⫻ [⫺2.5, 2.5]. (b) The subregion

[⫺1.88, ⫺1.6] ⫻ [⫺0.52, ⫺0.24], which is the box in part (a). (c) The subregion

[⫺1.88, ⫺1.86] ⫻ [⫺0.52, ⫺0.5], the box in the lower left corner of part (b).

165

F RACTALS

f (R)

(a) (b)

Figure 4.9 Construction of a fractal basin boundary.

(a) The image of the rectangle R is an S-shaped strip. Points that map outside and

to the left of R are attracted to the sink A

, and points that map outside and to the

right of R are attracted to the sink A

. (b) The shaded regions are mapped out of

the rectangle in one iteration. Each of the three remaining vertical strips will lose

4 shaded substrips on the next iteration, and so on. The points remaining inside

forever form a Cantor set.

on whether the third iterate goes to the left, goes to the right, or stays in the

square.

This analysis implies that the subset of R that remains inside the square for

n iterates consists of 3

vertical strips. Each of these segments has three substrips

that will remain inside R for a total of n ⫹ 1 iterates. If we have set up the map

in a reasonable manner, the width of the vertical strips at the nth stage will

shrink geometrically to zero as n tends to inﬁnity. Thus we have a Cantor set

construction; that is, there is a Cantor set of vertical curves whose images will

remain inside R for all future times. Each of these vertical curves stretches from

the top of the square to the bottom, and each point in the union of the curves

has nearby points which go to A

and nearby points which go to A

. Therefore,

the Cantor set of vertical curves is the boundary between the basin of A

and the

basin of A

E XAMPLE 4.12

(Julia sets.) We return to the quadratic map, but with a difference: We now

view it as a function of one complex variable. Let P

(z) ⫽ z

⫹ c, where z is a

complex variable and c ⫽ a ⫹ bi is a complex constant. Notice that P

is a planar

map; one complex variable z ⫽ x ⫹ yi is composed of two real variables, x and y.

Multiplication of two complex numbers follows the rule

(u ⫹ vi)(x ⫹ yi) ⫽ ux ⫺ vy ⫹ (uy ⫹ vx)i

166

4.4 FRACTAL B ASIN B OUNDARIES

where i

⫽⫺1. In terms of real variables,

(x ⫹ yi) ⫽ (x ⫹ yi)

⫹ a ⫹ bi ⫽ x

⫺ y

⫹ a ⫹ (2xy ⫹ b)i.

We begin by considering the dynamics of this complex map when the

parameter c ⫽ 0. Then the map P

(z) ⫽ z

has an attracting ﬁxed point at z ⫽ 0

whose basin of attraction is 兵z : |z| ⬍ 1其, the interior of the unit disk. A point on

the unit circle

S ⫽ 兵z : |z| ⫽ 1其

maps to another point on the unit circle (the angle is doubled). The orbit of any

point in 兵z : |z| ⬎ 1其, the exterior of the unit disk, diverges to inﬁnity. The circle

S forms the boundary between the basin of z ⫽ 0 and basin of inﬁnity. Notice

that points in the invariant set S are not in either basin.

For different settings of the constant c, z ⫽ 0 will no longer be a ﬁxed

point. Since we are considering all complex numbers, the equation z

⫹ c ⫽ z

will have roots. Therefore P

has ﬁxed points. In fact, there is an easy way of

ﬁnding all the attracting ﬁxed and periodic points of P

, due to a theorem of

Fatou: Every attracting cycle for a polynomial map P attracts at least one critical

point of P. Actually, Fatou proved the result for all rational functions (functions

that are quotients of polynomials). Compare this statement with Theorem 3.29

of Chapter 3. Since our function P

has only one critical point (z ⫽ 0), it can

have at most one attracting periodic orbit.

Sometimes P

has no attractors. Consider, for example, P

⫺i

(z) ⫽ z

⫺ i.

Then P

(0) ⫽⫺1 ⫺ i, which is a repelling period-two point. We need look no

further for an attractor.

Recognizing the important role that the orbit of 0 plays in the dynamics of

, we deﬁne the Mandelbrot set as follows:

M ⫽ 兵c : 0 is not in the basin of inﬁnity for the map P

(z) ⫽ z

⫹ c其.

We have seen that c ⫽ 0andc ⫽⫺i are in the Mandelbrot set. Check that c ⫽ 1

is not. Figure 4.10 shows the set in white, where the number c ⫽ a ⫹ bi is plotted

in the plane as the point (a, b). See Color Plates 11–12 for color versions of the

Mandelbrot set.

For each c in the Mandelbrot set, there are orbits of P

that remain bounded

and orbits that do not. Therefore, the boundary of the basin of inﬁnity is non-

empty. This boundary is called the Julia set of P

, after the French mathematician

G. Julia. Technically, the Julia set is deﬁned as the set of repelling ﬁxed and

167

F RACTALS

1.0

⫺1.0

⫺1.50.6

Figure 4.10 The Mandelbrot set.

A constant c is colored white if the orbit of z

⫹ c with initial value 0 does not

diverge to inﬁnity.

periodic points together with the limit points of this set. In the case of polynomials,

however, the two deﬁnitions coincide.

In Figure 4.11 we show Julia sets for values of c inside the Mandelbrot set.

For c ⫽⫺0.17 ⫹ 0. 78i, there is a period-three sink, whose basin is shown in

Figure 4.11(a). Each point in white is attracted to the period-three sink. The

points in black diverge to inﬁnity. The boundary between these two basins is the

Julia set. This picture shows many “rabbits” and other interesting shapes. The

rabbit at the top of the picture is magniﬁed in part (b). Part (c) shows a Julia set

which is the boundary of the basin of a period-ﬁve sink.

The constants c used to make Figures 4.11(a) and (c) lie in distinctive

places in the Mandelbrot set. Each c chosen from the small lobe at the top of the

Mandelbrot set, such as c ⫽⫺0.17 ⫹ 0.78i, creates a white basin of a period-three

attractor, as in Figure 4.11(a). The period-ﬁve lobe lies at about 2 o’clock on the

Mandelbrot set; it contains c ⫽ 0.38 ⫹ 0.32i, whose period-ﬁve sink is shown in

Figure 4.11(c). Part (d) of the ﬁgure has a period-11 sink. The value of c used

lies in the period-11 lobe, which is almost invisible in Figure 4.10. For more on

Julia sets and the Mandelbrot set, consult (Devaney, 1986), (Devaney and Keen,

1989), or (Peitgen and Richter, 1986).

168

4.4 FRACTAL B ASIN B OUNDARIES

1.5

⫺1.5

⫺1.51.5

(a)

1.09

0.89

⫺0.19 0.01

(b)

1.3

⫺1.3

⫺1.31.3

(c)

1.3

⫺1.3

⫺1.31.3

(d)

Figure 4.11 Julia sets for the map

(

) ⴝ

ⴙ

(a) The constant is set at c ⫽⫺0.17 ⫹ 0.78i. The white points are the basin of

a period-three sink, marked with crosses, while the black points are the basin of

inﬁnity. The fractal basin boundary between black and white is the Julia set. (b) The

uppermost rabbit of (a) is magniﬁed by a factor of 15. (c) c ⫽ 0.38 ⫹ 0.32i. The white

points are the basin of a period-ﬁve sink, marked with crosses. (d) c ⫽ 0.32 ⫹ 0.043i.

The white points are the basin of a period-11 sink.

169

F RACTALS

➮ COMPUTER EXPERIMENT 4.3

Draw the Julia set for f(z) ⫽ z

⫹ c with c ⫽ 0.29 ⫹ 0.54i. Plot the basin

of inﬁnity in black. Divide the square [⫺1.3, 1.3] ⫻ [⫺1.3, 1.3] into an N ⫻ N

grid for N ⫽ 100. For each of the N

small boxes, iterate f(z) using the center

of the box as initial value. Plot a black point at the box (or better, ﬁll in the

box) if the iteration diverges to inﬁnity; plot a different color if the iteration stays

bounded. Your picture should bear some resemblance to the examples in Figure

4.11. What is the bounded attracting periodic sink for this Julia set? Locate c in

the Mandelbrot set. Increase N for better resolution. Further work: Can you ﬁnd

a constant c such that f(z) ⫽ z

⫹ c has a period-six sink?

E XAMPLE 4.13

(Riddled basins.) In the examples we have studied so far, a basin of attraction

is an open set. In particular, it contains entire disk neighborhoods. In this example,

each disk, no matter how small, contains a nonzero area of points whose orbits

move to different attractors. A basin that is shot through with holes in this sense

is called a riddled basin.

Deﬁne the map

f(z) ⫽ z

⫺ (1 ⫹ ai)z, (4.3)

where z ⫽ x ⫹ iy is a complex variable, and z ⫽ x ⫺ iy denotes the complex

conjugate of z. The number a is a parameter that we will specify later. The map

can be rewritten in terms of the real and imaginary parts, as

f(x, y) ⫽ (x

⫺ y

⫺ x ⫺ ay, 2xy ⫺ ax ⫹ y).

The line N

⫽ 兵z ⫽ x ⫹ iy : y ⫽ a 2其 is invariant under f, meaning that

any point on that line maps back on the line:

f(x ⫹ ia 2) ⫽ (x ⫹ ia 2)

⫺ (1 ⫹ ai)(x ⫺ ia 2)

⫽ x

⫺ 3a

 4 ⫺ x ⫹ i(a 2). (4.4)

If we consider the map restricted to that line, the above formula shows that it is

the one-dimensional quadratic map, g(x) ⫽ x

⫺ x ⫺ 3a

 4.

170

4.4 FRACTAL B ASIN B OUNDARIES

✎ E XERCISE T4.7

Show that the one-dimensional map g(x) ⫽ x

⫺ x ⫺ 3a

 4 is conjugate to

the map h(w) ⫽ w

⫺ c, where the constant c ⫽ 3(1 ⫹ a

) 4.

Deﬁne the lines N

and N

to be the result of rotating N

clockwise through

120

◦

and 240

◦

, respectively. It can be checked that the map on N

is the same

as the map on N

, except that the images lie on N

, and vice versa for the map

on N

.ThusN

and N

map to one another with quadratic one-dimensional

dynamics. The second iterate f

on N

is exactly g

,andthesameforN

In Figure 4.12 the three lines are shown in white along with three basins of

attraction, for a particular parameter value a ⫽ 1.0287137 ..., which is a value of

a such that c satisﬁes the equality c

⫺ 2c

⫹ 2c ⫺ 2 ⫽ 0. This value is chosen so

that the quadratic map h(w) ⫽ w

⫺ c,towhichg is conjugate, has the property

that h

(0) is a ﬁxed point. The reason for requiring this is hard to explain for now,

Figure 4.12 The riddled basin.

There are three attractors in the shaded region. Any disk of nonzero radius in this

region, no matter how small, contains points from all 3 basins. Color Plate 2 is a

color version of this ﬁgure.

171

F RACTALS

but we will see in Chapter 6 that when the critical point maps in three iterates to

a ﬁxed point for a one-dimensional map, a continuous natural measure is created,

which turns out to be desirable for this application.

The three attractors for this system are contained in the union of the three

lines. The ﬁrst, A

, is the union of two subintervals of the line N

, and the second,

, is the union of two slanted intervals that intersect A

. The third, A

,isan

“X” at the intersection of the lines N

and N

Figure 4.12 shows the basin of inﬁnity in white, and the basins of A

, A

and A

in dark gray, light gray, and black. The basins of all three attractors have

nonzero area, and are riddled. This means that any disk of nonzero radius in the

shaded region, no matter how small, has points from all 3 basins. Proving this fact

is beyond the scope of this book. Color Plate 2 is a color version of this ﬁgure,

which shows more of the detail.

The message of this example is that prediction can be difﬁcult. If we want

to start with an initial condition and predict the asymptotic behavior of the

orbit, there is no limit to the accuracy with which we need to know the initial

condition. This problem is addressed in Challenge 4 in a simpler context: When

a basin boundary is fractal, the behavior of orbits near the boundary is hard to

predict. A riddled basin is the extreme case when essentially the entire basin is

made up of boundary.

4.5 FRACTAL DIMENSION

Our operational deﬁnition of fractal was that it has a level of complication that

does not simplify upon magniﬁcation. We explore this idea by imagining the

fractal lying on a grid of equal spacing, and checking the number of grid boxes

necessary for covering it. Then we see how this number varies as the grid size is

made smaller.

Consider a grid of step-size 1 n on the unit interval [0, 1]. That is, there are

grid points at 0, 1 n, 2 n,...,(n ⫺ 1) n, 1. How does the number of grid boxes

(one-dimensional boxes, or subintervals) depend on the step-size of the grid? The

answer, of course, is that there are n boxes of grid size 1 n. The situation changes

slightly if we consider the interval [0, 8]. Then we need 8n boxes of size 1 n.The

common property for one-dimensional intervals is that the number of boxes of

size

⑀

required to cover an interval is no more than C(1

⑀

), where C is a constant

depending on the length of the interval. This proportionality is often expressed by

saying that the number of boxes of size

⑀

scales as 1

⑀

, meaning that the number

172

4.5 FRACTAL D IMENSION

of boxes is between C



⑀

and C



⑀

,whereC

and C

are ﬁxed constants not

depending on

⑀

The square 兵(x, y):0ⱕ x, y ⱕ 1其 of side-length one in the plane can be

covered by n

boxes of side-length 1 n. It is the exponent 2 that differentiates this

two-dimensional example from the previous one. Any two-dimensional rectangle

in ⺢

can be covered by C(1

⑀

)

boxes of size

⑀

. Similarly, a d-dimensional region

requires C(1

⑀

)

boxes of size

⑀

The constant C depends on the rectangle. If we consider a square of side-

length 2 in the plane, and cover by boxes of side-length

⑀

⫽ 1 n,then4(1

⑀

)

boxes are required, so C ⫽ 4. The constant C can be chosen as large as needed,

as long as the scaling C(1

⑀

)

holds as

⑀

goes to 0.

We are asking the following question. Given an object in m-dimensional

space, how many m-dimensional boxes of side-length

⑀

does it take to cover the

object? For example, we cover objects in the plane with

⑀

⫻

⑀

squares. For objects

in three-dimensional space, we cover with cubes of side

⑀

. The number of boxes,

in cases we have looked at, comes out to C(1

⑀

)

,whered is the number we

would assign to be the dimension of the object. Our goal is to extend this idea

to more complicated sets, like fractals, and use this “scaling relation” to deﬁne

the dimension d of the object in cases where we don’t start out knowing the

answer.

Notice that an interval of length one, when viewed as a subset of the plane,

requires 1

⑀

two-dimensional boxes of size

⑀

to be covered. This is the same

scaling that we found for the unit interval considered as a subset of the line, and

matches what we would ﬁnd for a unit interval inside ⺢

for any integer m.This

scaling is therefore intrinsic to the unit interval, and independent of the space

in which it lies. We will denote by N(

⑀

) the number of boxes of side-length

⑀

needed to cover a given set. In general, if S is a set in ⺢

, we would like to say

that S is a d-dimensional set when it can be covered by

⑀

) ⫽ C(1

⑀

)

boxes of side-length

⑀

, for small

⑀

. Stated in this way, it is not required that the

exponent d be an integer.

Let S be a bounded set in ⺢

. To measure the dimension of S,welayagrid

of m-dimensional boxes of side-length

⑀

over S. (See Figure 4.13.) Set N(

⑀

) equal

to the number of boxes of the grid that intersect S. Solving the scaling law for the

173

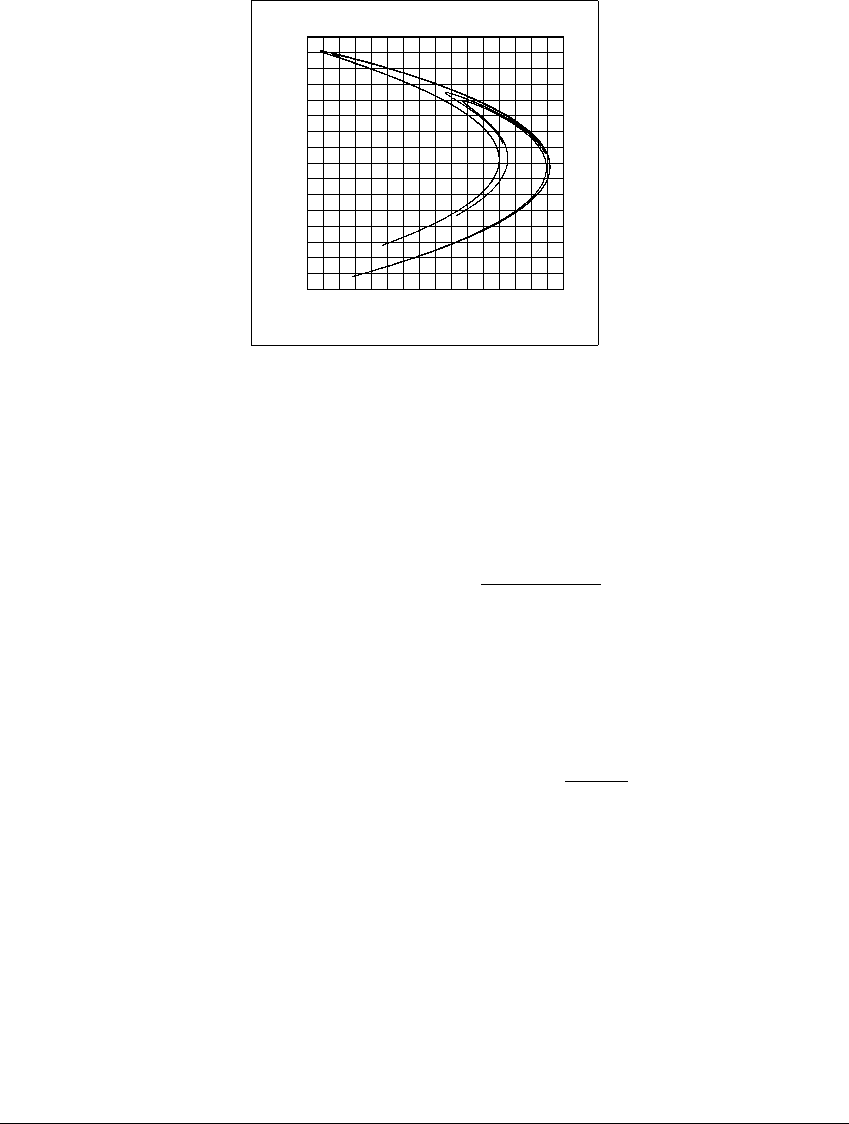
F RACTALS

-2

-2 0 2

Figure 4.13 Grid of boxes for dimension measurement.

The H

enon attractor of Example 4.10 is shown beneath a grid of boxes with side-

length

⑀

⫽ 1 4. Of the 256 boxes shown, 76 contain a piece of the attractor.

dimension d gives us

d ⫽

ln N(

⑀

) ⫺ ln C

ln(1

⑀

)

If C is constant for all small

⑀

, the contribution of the second term in the

numerator of this formula will be negligible for small

⑀

. This justiﬁes the following:

Deﬁnition 4.14 A bounded set S in ⺢

has box-counting dimension

boxdim(S) ⫽ lim

⑀

→0

ln N(

⑀

)

ln(1

⑀

)

when the limit exists.

We can check that this deﬁnition of dimension gives the correct answer for

a line segment in the plane. Let S be a line segment of length L. The number of

boxes intersected by S will depend on how it is situated in the plane, but roughly

speaking, will be at least L

⑀

(if it lies along the vertical or the horizontal) and no

more than 2L

⑀

(if it lies diagonally with respect to the grid, and straddles pairs

of neighboring boxes). As we expect, N(

⑀

) scales as 1

⑀

for this one-dimensional

set. In fact, N(

⑀

) is between L times 1

⑀

and 2L times 1

⑀

. This remains true for

inﬁnitesimally small

⑀

. Then Deﬁnition 4.14 gives d ⫽ 1.

174