Alligood K., Sauer T., Yorke J.A. Chaos: An Introduction to Dynamical Systems
Подождите немного. Документ загружается.

C HAOS
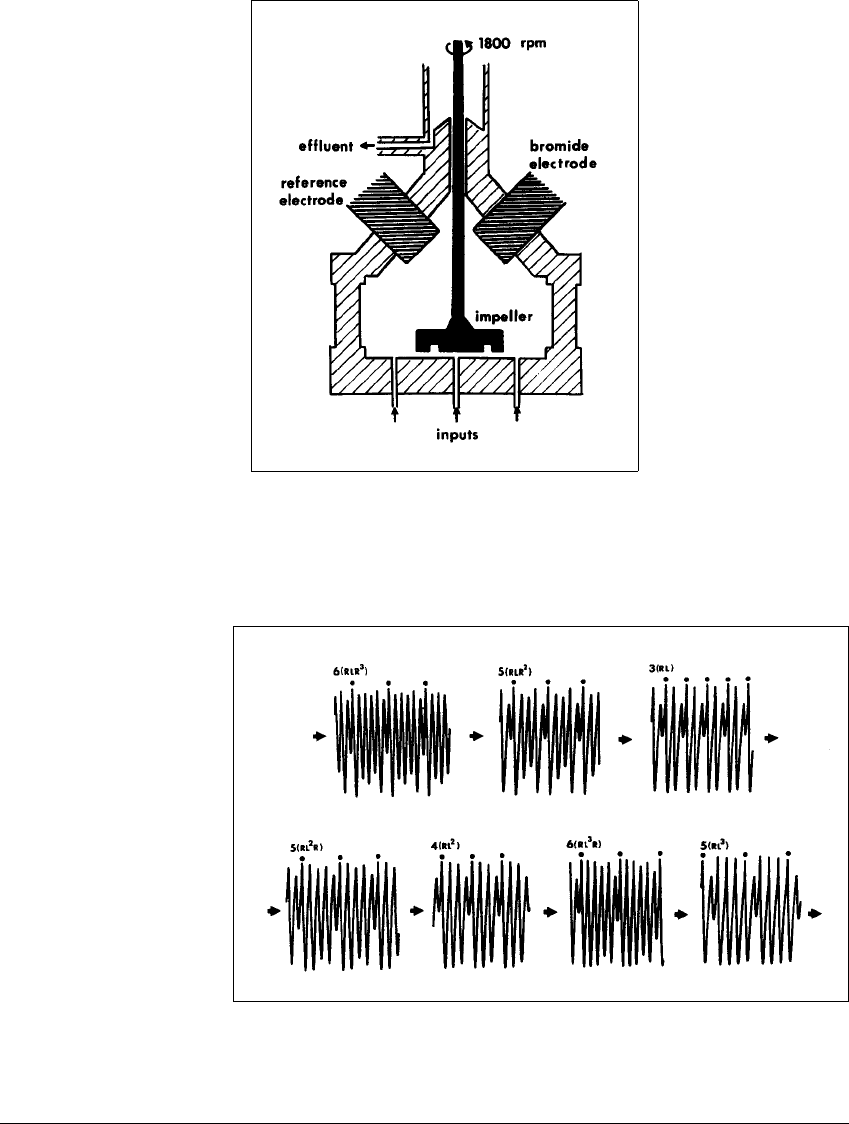
Figure 3.17 A schematic diagram of the chemical reactor used for the BZ
reaction.
The volume of the cylindrically symmetric chamber is 33 cc.
Figure 3.18 Periodic oscillations of the bromide concentration.
The horizontal axis is time, and the concentration is graphed vertically. Dots are
shown to mark the period of the oscillation.
144

L AB V ISIT 3
The time series of concentration in Figure 3.18 are quite compelling; cer-
tainly they reflect a periodic state in the chemistry. Chaotic states present a greater
challenge to data analysis. How can we see deterministic structure, if it exists, in a
single time series recording of bromide concentration? A solution to this problem
is illustrated in Figure 3.19. The bromide concentration B(t
i
) is plotted against
two delayed versions of itself, B(t
i
⫹ T)andB(t
i
⫹ 2T), in a 3-D plot. (The time
unit is seconds; T ⫽ 8.8 sec.) This type of plot, called a delay coordinate plot,
reveals the characteristic shape of a chaotic attractor. Delay coordinate plots are
discussed in more detail in Chapter 13.
From the plot, a one-dimensional map can be constructed as a Poincar
´
e
return map. Using the plane fragment shown, the horizontal coordinates of suc-
cessive intersections are recorded. If x denotes the bromide concentration at
one intersection, then f(x) is the concentration at the next intersection. The
resulting pairs of points (x, f(x)) are plotted in Figure 3.20. Using standard ap-
proximation techniques, a function f was drawn through the points that best fit
the experimental data.
Figure 3.19 Reconstruction of dynamics from the bromide time series.
The three coordinates are the concentrations at three equally spaced time intervals.
The Poincar
´
e section, shown as a plane, intersects the data essentially in a curve,
which allows a reduction to the one-dimensional map of Figure 3.20.
145
C HAOS
Figure 3.20 One-dimensional map reconstructed from the time series.
A spline fit was made to the data points from Poincar
´
e map of Figure 3.19.
The one-dimensional map derived from this process is quite easy to analyze
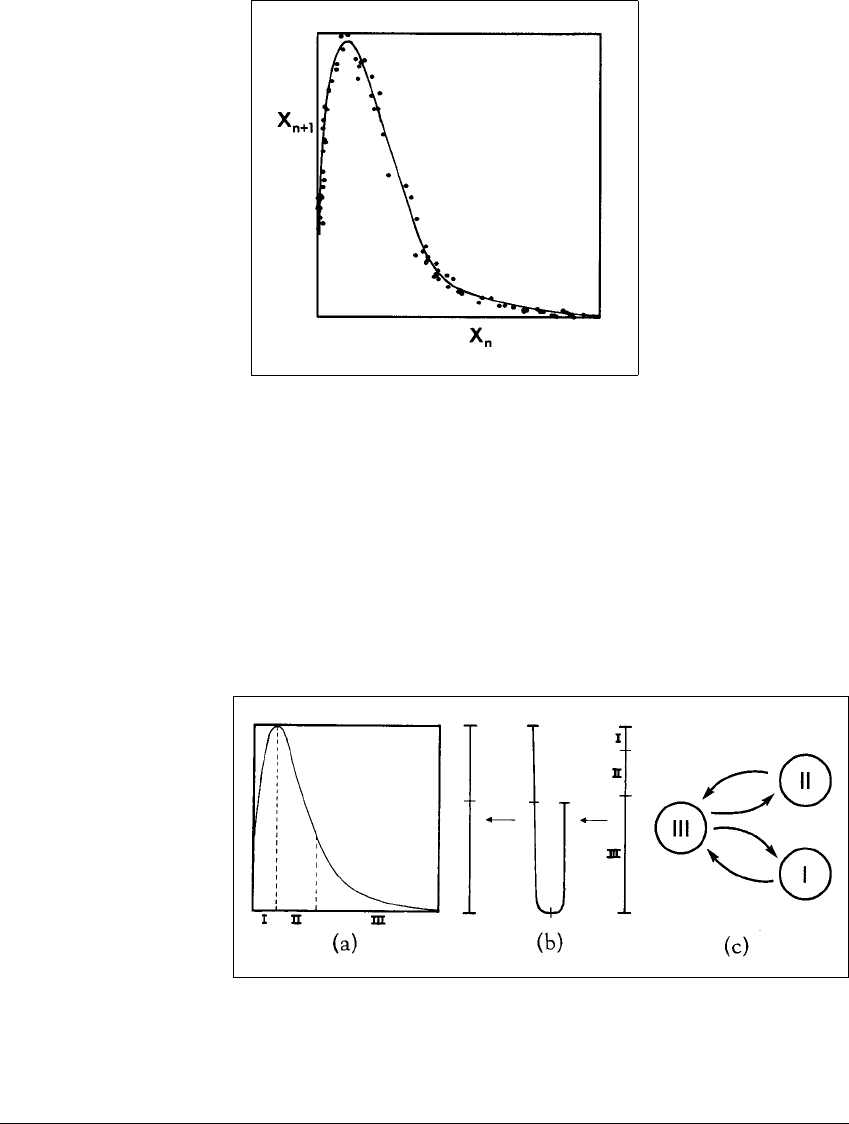
using the symbol sequences we have discussed in Chapter 3. The interval can be
divided into three subintervals I, II, and III. The effect of one iteration of the map
is shown in Figure 3.21. The subintervals I and II each stretch across subinterval
III, and III stretches across both I and II. The result is a transition graph as in
Figure 3.21. Using Figure 3.21 and Sharkovskii’s Theorem, one can find the set
Figure 3.21 Symbol analysis of the one-dimensional map.
(a) The one-dimensional map fit from the data in Figure 3.20. (b) Schematic
representation of the stretching and folding of the interval on the three subintervals
I, II, and III. (c) Transition graph of the dynamics.
146

L AB V ISIT 3
of periods possessed by periodic orbits of the system: all periods that are an even
number of returns to the Poincar
´
e surface of section shown in Figure 3.19.
An attempt was made to calculate the Lyapunov exponent from the one-
dimensional map of Figure 3.20. It was found that the calculation of this number
was very difficult, in the sense that small changes in the way the function approx-
imation was made had large effects on the Lyapunov exponent that was derived.
A careful estimate turned up
1
⬇ 0.3 ⫾ 0.1.
Partway through the series of experiments by the Texas group, they had an
opportunity to upgrade the laboratory apparatus, significantly improving the con-
trol of the conditions of the reaction. When they restarted the experiments, they
found that the same experimental conditions gave different results. In particular,
the one-dimensional map of Figure 3.20, although still chaotic, had significantly
changed.
A detailed analysis showed that the difference arose not from changes in
equipment but primarily from differences in the malonic acid reagent, which
now came from a new supplier. The group eventually bought malonic acid of
99.5% purity from seven different vendors, and found that each yielded its own
one-dimensional map. Results within any given sample of malonic acid were re-
producible over long periods of time, even with modified experimental apparatus.
Finally, the research group purified the different lots of malonic acid, and again
found identical dynamics independent of the supplier as well as the particular
purification procedure. As a result, there is great confidence in the reproducibility
of the results. One of the several morals of this story is the extreme sensitivity of
the dynamics with respect to system parameters.
147

C HAPTER F OUR
Fractal s
A
FRACTAL is a complicated geometric figure that, unlike a conventional com-
plicated figure, does not simplify when it is magnified. In the way that Euclidean
geometry has served as a descriptive language for the classical mechanics of mo-
tion, fractal geometry is being used for the patterns produced by chaos. Trajectories
of the two-body problem, for example, consist of conic sections: ellipses, parabo-
las, and hyperbolas. Chaotic attractors, on the other hand, often have features
repeated on many length or time scales.
Scientists know a fractal when they see one, but there is no universally
accepted definition. The term “fractal” was coined in the 1960’s by B. Mandelbrot,
a mathematician at IBM. It is generally acknowledged that fractals have some or
all of the following properties: complicated structure at a wide range of length
scales, repetition of structures at different length scales (self-similarity), and a
149
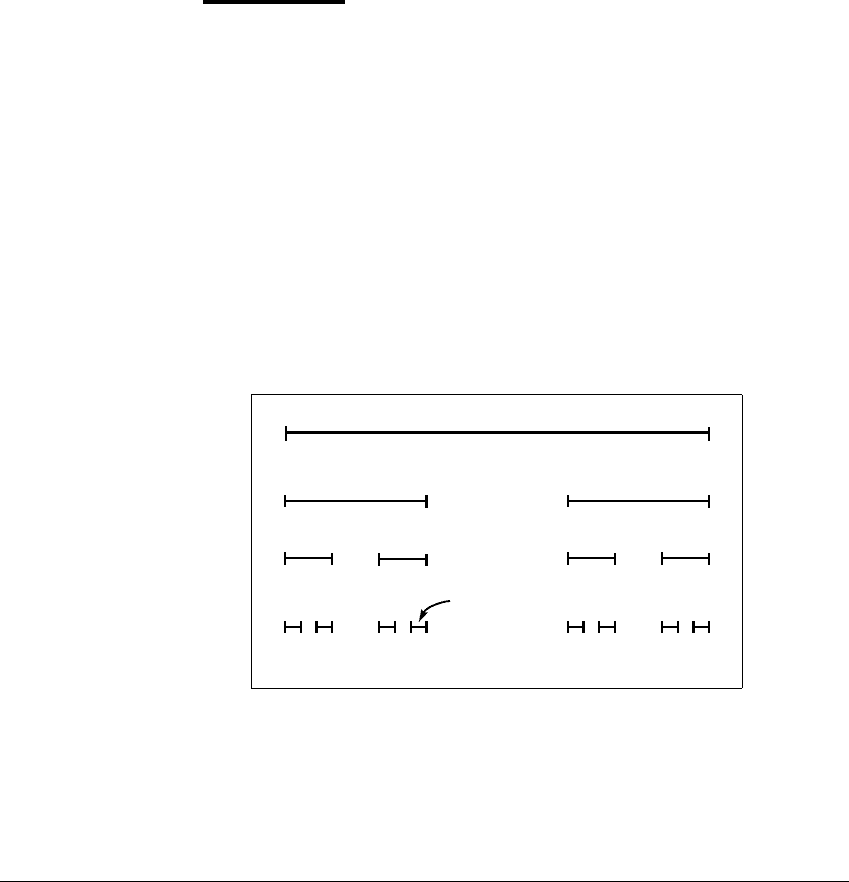
F RACTALS
“fractal dimension” that is not an integer. We will exhibit and analyze these
properties for several examples that are generally agreed to be fractals, and in
so doing define fractal dimension. Perhaps the simplest geometric object that
deserves to be called a fractal is a Cantor set.
4.1 CANTOR SETS
E XAMPLE 4.1
Begin with the unit interval I ⫽ [0, 1] and make a new set according
to the following instructions. (See Figure 4.1.) First remove the open interval
(1 3, 2 3), the middle third of I. The set of points that remain after this first step
will be called K
1
.ThesetK
1
is the union [0, 1 3] 傼 [2 3, 1]. In the second step,
remove the middle thirds of the two segments of K
1
. That is, remove (1 9, 2 9) 傼
(7 9, 8 9) and set K
2
⫽ [0, 1 9] 傼 [2 9, 3 9] 傼 [6 9, 7 9] 傼 [8 9, 1] to be what
remains after the first two steps. Delete the middle thirds of the four remaining
segments of K
2
to get K
3
. Repeating this process, the limiting set K ⫽ K
⬁
is called
the middle-third Cantor set.ThesetK is the set of points that belong to all of
the K
n
.
0
1
0
1
1
0
0
1
1/3
2/3
1/9 2/9
1/3
2/3 7/9
8/9
.0 .2
.00 .02 .20 .22
.022
Figure 4.1 Construction of the middle-third Cantor set.
In step 1, the middle third of the unit interval is removed. In further steps, the
middle third of every remaining subinterval is removed. Here three steps are shown.
The points that are never removed make up the Cantor middle-third set. The set
marked .02 consists of all numbers in the unit interval whose ternary expansion
begins with .02.
150

4.1 CANTOR S ETS
What is the length of the set K? First of all, the set K is contained in K
n
for each n.JustasK
1
consists of 2 intervals of length 1 3, and K
2
consists of
4 intervals of length 1 9, in general K
n
consists of 2
n
intervals, each of length
(1 3)
n
, so its total length is (2 3)
n
. Hence K can be “covered” by a collection
K
n
of intervals whose total length can be made as small as you like. For example,
K
40
has length less than 10
⫺6
.SinceK
⬁
is a subset of all of these sets, we say that
K
⬁
has length zero.
Although we doubt anyone disagrees on determining the length of an
interval [a, b], it can be a perplexing task to assign length to every possible set of
points. There is a field of mathematics called measure theory that tries to solve
this problem. We return to the concept of measure in Chapter 6. For now, it is
sufficient to say that there is a definition of zero length, or measure zero, that is
useful in practice.
AsetS is said to have measure zero if it can be covered with intervals
whose total length is arbitrarily small. In other words, for each predetermined
⑀
⬎ 0, one can find a countable collection of intervals containing S whose total
length is at most
⑀
. The logic is that if the set in question can be viewed as a
subset of sets with ordinary length as small as you want, then the set should be
assigned a length of zero.
The set 兵1, 2, 3,...,10其 has measure zero, since for any predetermined
⑀
⬎ 0, the set can be covered by 10 intervals of length
⑀
10 centered at the 10
integers. Therefore it has a covering set of length
⑀
, for
⑀
as small as you want. To
show that the set 兵1, 2, 3,...其 of natural numbers has measure zero takes a little
more work. Given the predetermined
⑀
, consider the countable set of intervals
of length 2
⫺n
⑀
centered at the natural number n. The sum total of the interval
lengths is
⑀
, as required. Finally, since the Cantor set K is covered by the set K
n
of
length (2 3)
n
, which is arbitrarily small for large enough n, we can say that the
Cantor set K has measure zero.
Although K has no length, it contains many points of the unit interval.
Obviously, 0 and 1 belong to K. Similarly, both endpoints of any deleted middle
third belong to K. After all, they will never end up in the middle third of a
remaining subinterval at any stage of the construction.
Surprisingly, the endpoints make up only an insignificant portion of the
points of K. For example, the number 1 4, although never an endpoint of a
subinterval of the construction, belongs to the middle-third Cantor set K.Tosee
this, it is useful to express the numbers between 0 and 1 in base-3 representation.
If 0 ⱕ r ⱕ 1, then r can be written
r ⫽ a
1
⫻ 3
⫺1
⫹ a
2
⫻ 3
⫺2
⫹⭈⭈⭈⫹a
n
⫻ 3
⫺n
⫹⭈⭈⭈
for numbers a
k
⫽ 0, 1, or 2. The a
k
’s are the ternary digits of r.
151

F RACTALS
To find the base 3 representation of a number r between 0 and 1, proceed
as follows. Multiply r by 3, and take the integer part of the result (which is 0,
1, or 2) as a
1
. Then take the fractional part and repeat this step to get a
2
,etc.
For example, the fraction 1 3 has a base-3 representation of .1, and 1 2has
a representation of .
1, that is, all digits are 1. This is analogous to the binary
representations introduced in Chapter 3.
This representation for r is unique except for numbers r ⫽ .a
1
a
2
...a
n
with
a finite base-3 representation. By a finite base-3 representation, we mean that the
ternary digit a
n
is nonzero, and 0 ⫽ a
n⫹1
⫽ a
n⫹2
⫽ ....Thenr is represented by
exactly two base-3 expansions:
r ⫽ .a
1
a
2
...a
n
⫽ .a
1
a
2
...(a
n
⫺ 1)222 .....
The subinterval [1 3, 2 3) consists of the points whose base-3 representa-
tions satisfy a
1
⫽ 1. The number 1 3 can be expressed in two ways, as .1 ⫽ .02
in base 3. Therefore, the set K
1
⫽ [0, 1 3] 傼 [2 3, 1] consists of all numbers in
[0, 1] that can be represented in base 3 with a
1
⫽ 0 or 2. Similarly the set
K
2
⫽ [0, 1 9] 傼 [2 9, 1 3] 傼 [2 3, 7 9] 傼 [8 9, 1]
from the second step of the Cantor set construction is a set that consists of all
numbers having representations with a
1
and a
2
each being either 0 or 2. We can
ask what the analogous property is for K
n
, and then ask what property a number
must have if it is simultaneously in all of the K
n
,thatis,ifitisinK
⬁
.Fromthis
reasoning follows a simple theorem.
Theorem 4.2 The middle-third Cantor set K consists of all numbers in the
interval [0, 1] that can be represented in base 3 using only the digits 0 and 2.
For example, the base-3 number r ⫽ .
02 belongs to K.Notethat
r ⫽ 0 ⫻ 3
⫺1
⫹ 2 ⫻ 3
⫺2
⫹ 0 ⫻ 3
⫺3
⫹ 2 ⫻ 3
⫺4
⫹ ...
⫽
2
9
(1 ⫹ 3
⫺2
⫹ 3
⫺4
⫹ ...)
⫽
2
9
1
1 ⫺ 1 9
⫽ 1 4.
As mentioned above, some numbers have two base-3 representations: for
example, one-third can expressed as either .0
2or.1 in ternary expansion. How-
ever, each number in K has exactly one representation that includes no 1’s.
152

4.1 CANTOR S ETS
We have been viewing the real numbers [0, 1] in terms of their base-3
expansions, but each number also has a binary expansion. That is, the number
can be expressed using base-2 arithmetic as an infinite sequence of two symbols,
0 and 1. Therefore Theorem 4.2 shows that there is a one-to-one correspondence
between the set [0, 1] and part of the Cantor set K, which is somewhat surprising
in view of the fact that K has no length. In particular, K is a typical example of
what is called an uncountable set, which we define next.
The idea of putting two sets in a one-to-one correspondence is the basis
of counting. Saying that a particular deck contains 52 cards means that we
can associate the cards with the set of numbers 兵1, 2,...,52其. Saying that the
correspondence is “one-to-one” means that for each number there is exactly one
card. No cards are counted twice, but all are counted. Another way of expressing
a one-to-one correspondence with the set 兵1,...,52其 is to say that we can make
a list with 52 entries. If there is no finite list containing all elements of the set,
we call the set infinite.
Cantor took this idea of counting a step further. He called a set countably
infinite if it can be put in a one-to-one correspondence with the natural numbers
(positive integers). We will say that a set is countable if it is a finite set or a
countably infinite set. Another way to say this is that a set is countable if its
elements can be put in a finite or infinite list with each element listed exactly
once. We call a set uncountable if it is not countable.
For example, the set of positive even integers is a countable set, as is the
set of squares 兵1, 4, 9,...其. A little more thought shows that the set of (positive
and negative) integers is countable. Moreover, a subset of any countable set is
countable. Thus the set of prime numbers is countable, even though no one knows
an explicit formula for the nth prime number.
✎ E XERCISE T4.1
(a) Show that the union of two countable sets is countable. (b) Let
S
1
,S
2
,S
3
,... be a countable collection of countable sets. Show that the
union of the S
i
is countable.
The set of rational numbers (fractions m n between 0 and 1, where m and
n are nonzero integers) is countable. A scheme for counting the rational numbers
in the interval (0, 1] is illustrated in Figure 4.2. Notice that there are repetitions
in the ordering; for example, 1 2, 2 4, 3 6, etc., are all counted separately, so
the figure shows that the rationals are a subset of a countable set, and therefore
countable. Furthermore, once we know that the rationals in (n, n ⫹ 1] form
153

F RACTALS
1
/2
1
/3
2/3
1
/4
2/4
3/4
1
/5
2/5
3/5
4/5
1
/6
2/6
Figure 4.2 A scheme for counting the rationals.
The set of rational numbers is called countable because they can be put into a single
(infinite) list.
a countable set for each integer n, then the entire set of rational numbers is a
countable union of countable sets, which according to Exercise T4.1 is again a
countable set.
Another example of a countable set is the set of all numbers in the middle-
third Cantor set K having a finite number of ternary digits. Verify that these
numbers are the right-hand endpoints of the removed open intervals of the
Cantor set construction process. The correspondence could go as follows:
Natural number Number in
K
1 .2
2 .02
3 .22
4 .002
5 .022
6 .202
7 .222
.
.
.
.
.
.
154
