Alligood K., Sauer T., Yorke J.A. Chaos: An Introduction to Dynamical Systems

Подождите немного. Документ загружается.

C HAOS

Theorem 3.9 The tent map T has inﬁnitely many chaotic orbits.

Proof: Since the absolute value of the slope of T is 2 whenever it exists

(for x ⫽ 1 2), the Lyapunov exponent of an orbit of T is ln 2 whenever it is

deﬁned. Any orbit that avoids 1 2 and is not asymptotically periodic is therefore

a chaotic orbit.

Any asymptotically periodic orbit of the tent map must be eventually peri-

odic. The reason is that the derivative of T

at a period-k orbit is 2

, so all periodic

orbits are sources and attract no orbits. According to Exercise T3.5, an eventually

periodic orbit must have an eventually repeating itinerary. There are inﬁnitely

many nonrepeating itineraries that correspond to distinct chaotic orbits.

3.3 CONJUGACY AND THE LOGISTIC MAP

In the previous section we established the fact that the tent map T has chaotic

orbits. In this section we see that the logistic map G(x) ⫽ 4x(1 ⫺ x)alsohas

chaotic orbits, and in particular has a chaotic orbit that ﬁlls up (is dense in) the

unit interval.

Calculations for the Lyapunov exponent of the tent map were extremely

easy: since the absolute value of the slope is exactly 2 at every point (except the

point of nondifferentiability), the exponential separation factor is ln 2 at every

iteration. The logistic map is more challenging; clearly the slope varies from

iteration to iteration along typical orbits. The logistic map is a smooth map (no

points of nondifferentiability) with the same general shape as the tent map. Our

strategy will be to show that the similarity extends far enough that the logistic

map, as well as the tent map, has chaotic orbits. The concept of conjugacy is a

way of making the similarity explicit.

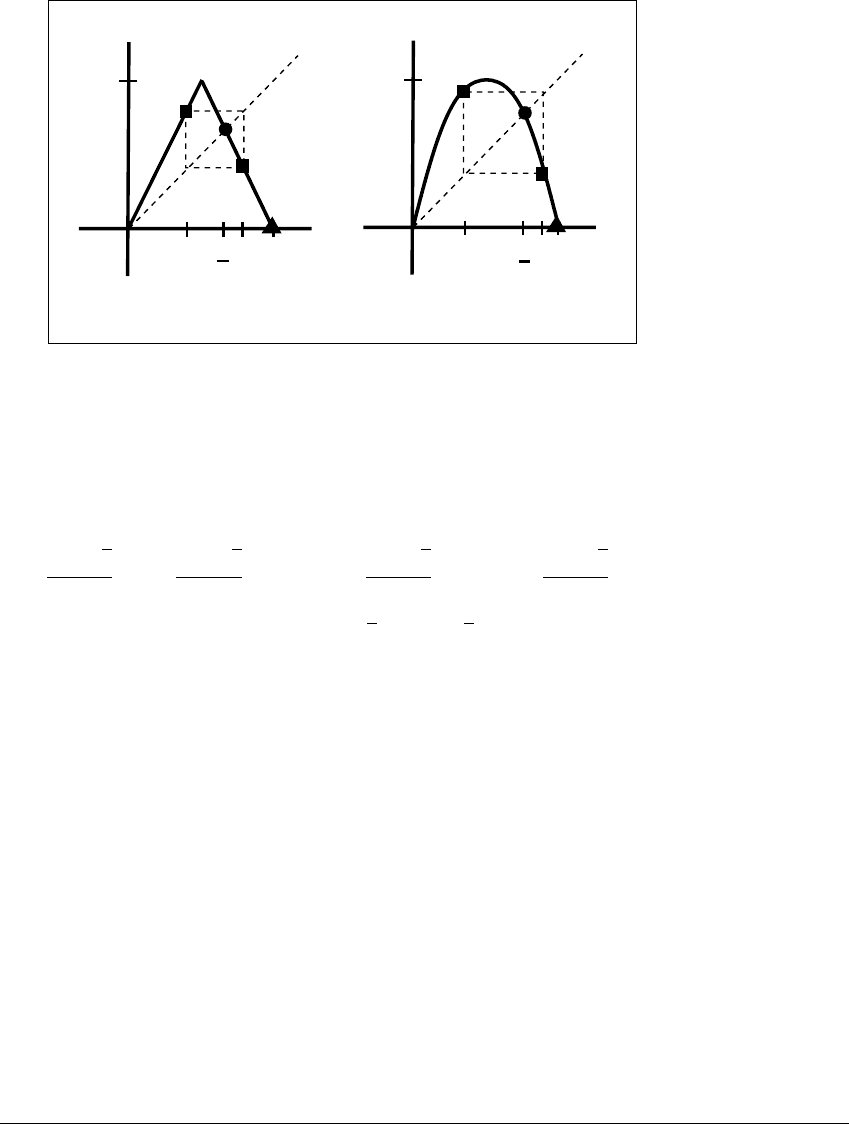
Figure 3.3 compares the two maps. They each have a critical point at

x ⫽ 1 2, which maps to 1 and then 0. Each has a ﬁxed point at zero, and one

other ﬁxed point: the tent map at x ⫽ 2 3 and the logistic map at x ⫽ 3 4. Each

has a single period-two orbit; the tent map has 兵0.4, 0.8其, and the logistic map has

兵(5 ⫺



5) 8, (5 ⫹



5) 8其. In each case, the period-two orbit lies in the same

relation to the other points; the left-hand point lies between the origin and the

critical point, and the right-hand point lies between the other ﬁxed point and 1.

More coincidences arise when we examine the stability of these orbits. The

derivative of T at its ﬁxed point x ⫽ 2 3 and the derivative of G at its ﬁxed

point x ⫽ 3 4 are both ⫺2, so both points are sources. The derivative of T

its period-two point x ⫽ 0.4isT



(0.4)T



(0.8) ⫽ (2)(⫺2) ⫽⫺4; likewise, the

114

3.3 CONJUGACY AND THE LOGISTIC M AP

.346

(a) (b)

Figure 3.3 Similarities in tent map and logistic map.

Both (a) the tent map and (b) the logistic map have a ﬁxed point (small circle) to

the right of the critical point x ⫽ 0.5. For each, the midpoint maps to 1 and then

to 0. Each has a single period-two orbit (small squares).

derivative of G

at its period-two point is





5 ⫹









5 ⫺





⫽



4 ⫺ 8



5 ⫹





4 ⫺ 8



5 ⫺





⫽ (⫺1 ⫺



5)(⫺1 ⫹



⫽ 1 ⫺ 5 ⫽⫺4.

Is the same sort of thing true for period-three orbits? (There should be two

such orbits, according to the periodic table, Table 1.3 of Chapter 1.) For period-

100 orbits? How far can we expect to push the similarity? At its extreme, it could

be expressed as follows: For each point x in the tent map domain [0, 1], there is

a speciﬁed companion point C(x) in the logistic map domain [0, 1] that imitates

its dynamics exactly. (Think of C as the “companion map”.) By that we mean

that the two image points of x and C(x) by their respective maps, the two points

T(x)andG(C(x)), are also companions. That would mean CT(x) ⫽ GC(x). If

there exists such a function C, then dynamical phenomena seen for the tent map

will be mimicked by its companions, or “conjugates”, in the logistic map. If C is

one-to-one, then the reverse is true as well.

Deﬁnition 3.10 The maps f and g are conjugate if they are related by

a continuous one-to-one change of coordinates, that is, if C ◦ f ⫽ g ◦ C for a

continuous one-to-one map C .

115

C HAOS

The conjugacy map C should be viewed as a correspondence between two

systems for assigning coordinates, similar to a translation from one language to

another. For example, we will show that the logistic map G and the tent map T

are conjugate by the one-to-one continuous map C(x) ⫽ (1 ⫺ cos

␲

x) 2, which

is shown in Figure 3.4. Notice that C is one-to-one from [0, 1] to [0, 1], which are

the domains of G and T.

To verify that G and T are conjugate by the conjugacy C, we need to check

that C(T(x)) ⫽ G(C(x)) for each x in [0, 1]. We will show how to do this for

0 ⱕ x ⱕ 1 2, and leave the other half to an exercise. The right hand side is

G(C(x)) ⫽ 4C(x)(1 ⫺ C(x))

⫽ 4



1 ⫺ cos

␲



1 ⫹ cos

␲



⫽ 1 ⫺ cos

␲

x ⫽ sin

␲

x. (3.1)

For the left side, we make use of the fact that T(x) ⫽ 2x for 0 ⱕ x ⱕ 1 2, so that

C(T (x)) ⫽

1 ⫺ cos

␲

T(x)

⫽

1 ⫺ cos 2

␲

⫽ sin

␲

x, (3.2)

where the last equality follows from the double angle formula for cos. Hence

G ◦ C(x) ⫽ C ◦ T(x) for 0 ⱕ x ⱕ 1 2.

y = C(x)

Figure 3.4 The conjugacy map.

The graph of C(x) ⫽ (1 ⫺ cos

␲

x) 2 is continuous and one-to-one. Since CT(x) ⫽

GC(x)forall0ⱕ x ⱕ 1, it is a conjugacy between the tent map and logistic map.

116

3.3 CONJUGACY AND THE LOGISTIC M AP

✎ E XERCISE T3.6

Check that C(T(x)) ⫽ G(C(x)) for all x in [1 2, 1], completing the veriﬁcation

of the conjugacy.

The meaning of the conjugacy between G and T is that there are two ways

to look at the map G—two ways to get from the domain of G to the range of G.

One way is to evaluate G(x); the second way is to ﬁnd the inverse image of x under

the one-to-one correspondence (which is C

⫺1

(x)), apply the map T,andthen

return to the original system by applying C. This amounts, of course, to saying

G(x) ⫽ CTC

⫺1

(x), which you proved in Exercise T3.6. In the second method,

the work of evaluating the map is done by T,andC is used to translate x in and

out of the language used by T.

The purpose of such a roundabout way of evaluating G is that T might be

easier to handle than G. Notice also that we can do multiple iterations of G this

way, with only one translation to and from T-language:

⫽ CTC

⫺1

CTC

⫺1

⭈⭈⭈CTC

⫺1

⫽ CT

⫺1

So if we have a lot of information about high iterates of T (which we do), we may

be able to make conclusions about high iterates of G.

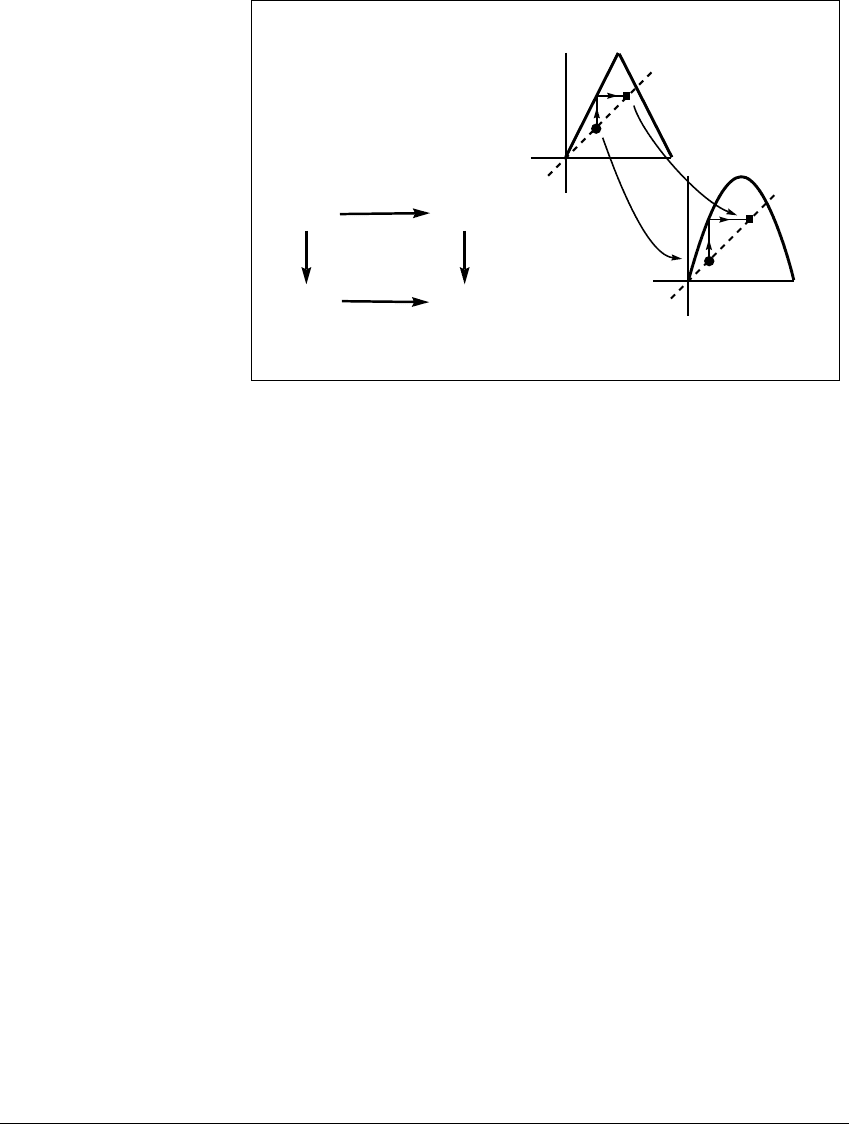
Figure 3.5(a) illustrates the directions of the maps. The conjugacy says that

if you begin with a number x in the upper left corner of the diagram, either choice

of direction to the lower right corner arrives at the same result. Either go across

ﬁrst and then down (which represents C(T(x))), or go down ﬁrst and then across

(which represents G(C(x))). Ending at the same number either way means that

C(T (x)) ⫽ G(C(x)). Figure 3.5(b) shows the correspondence between coordinate

systems in a more concrete way, for a typical x.

The fact that C is one-to-one means that there is a one-to-one correspon-

dence between a point x being mapped by T and the point C(x) being mapped

by G. Moreover, much of the behavior of one map corresponds to similar behavior

in the other. Suppose for instance that x is a ﬁxed point for T,sothatT(x) ⫽ x.

Then C (x) is a ﬁxed point for G,sinceGC(x) ⫽ CT(x) ⫽ C(x).

✎ E XERCISE T3.7

Show that if x is a period-k point for T,thenC(x) is a period-k point for G.

117

C HAOS

[0,1]

[0,1] [0,1]

n+1

=T(x

)

n+1

=G(y

)

(a) (b)

Figure 3.5 Two illustrations of the fact that the maps

and

are conjugate.

(a) Both ways of composing maps from upper left to lower right are equal. (b) If

⫽ C(x

) implies y

n⫹1

⫽ C(x

n⫹1

), then C is a conjugacy between the x-map and

the y-map.

The similar behavior of conjugate maps extends to stretching and shrinking

information. The chain rule says that



(T (x))T



(x) ⫽ G



(C(x))C



(x). (3.3)

Now suppose that x is a ﬁxed point for T and C



(x) ⫽ 0. Then T(x) ⫽ x implies

that T



(x) ⫽ G



(C(x)), meaning that the corresponding ﬁxed points x for the

map T and C(x) for the map G have the same derivative, and thus the same

stability. To get the same conclusion for period-two orbits, apply the conjugacy

to T

(x) to get CT(T(x)) ⫽ GC(T(x)) ⫽ GGC(x). Then apply the chain rule

to the result CT

(x) ⫽ G

C(x) to get



(x))(T

)



(x) ⫽ (G

)



(C(x))C



(x).

If x is a period-two point for T, and assuming C



(x) ⫽ 0, we have

)



(x) ⫽ (G

)



(C(x)),

meaning that the stability characteristics of the period-two orbit of T and the

corresponding period-two orbit of G are identical. This fact holds in general for

periodic orbits.

118

3.3 CONJUGACY AND THE LOGISTIC M AP

Theorem 3.11 Let f and g be conjugate maps, that is gC(x) ⫽ Cf(x) for all

x. If x is a period-k point for f, then C(x) is a period-k point for g. If also C



is never

zero on the periodic orbit of f, then

)



(C(x)) ⫽ (f

)



(x).

✎ E XERCISE T3.8

Use the chain rule (1.3) of Chapter 1 to provide a proof of Theorem 3.11.

The content of Theorem 3.11 is that the derivative at the ﬁxed point

x ⫽ 2 3ofT and C(x) ⫽ 3 4ofG are identical, as we stated above. These

points are both sources, since G



(3 4) ⫽ T



(2 3) ⫽⫺2. Note that Theorem

3.11 requires the assumption that the derivative C



is not zero on the orbit in

question. For example, the theorem does not apply to the other ﬁxed point x ⫽ 0

of T and its companion C(0) ⫽ 0ofG. The reason is that C



(0) ⫽ 0. The

derivatives T



(0) ⫽ 2andG



(0) ⫽ 4 disagree. A further application of Theorem

3.11 is the following fact:

All periodic points of the logistic map G are sources.

For any period-k point other than zero, the theorem applies and states that the

magnitude of the derivative of G

is 2

, the same as the corresponding period-k

point of T. Therefore all period-k points are sources with sensitivity to initial

conditions.

Conjugacies contain a great deal of information. If 兵x

,...,x

其 is a periodic

orbit of the logistic map G, its stability is determined by the derivative of G

evaluated at x

, which is the product G



) ⭈⭈⭈G



), according to the chain

rule. The derivatives of G on [0, 1] range between 0 and 4 (in magnitude)—there

is no a priori reason to expect the product of k of these numbers to have a simple

expression, or to have magnitude greater than one. In fact, the product amounts

to precisely 2

for a period-k orbit.

Finding a conjugacy between a map under study and an easier map is a

useful trick. Unfortunately, it is not always possible to ﬁnd such a conjugacy. For

the family g

(x) ⫽ ax(1 ⫺ x), no useful conjugacy exists for most values of the

parameter a.

Remark 3.12 There is one more fact (already used in Chapter 1) that is

a consequence of conjugacy. Because of the one-to-one correspondence C from

[0, 1] to itself, there is a direct correspondence between the itinerary subintervals

119

C HAOS

of Figure 3.2 (for the tent map) and Figure 1.12 of Chapter 1 (for the logistic map).

The logistic map subintervals are exactly the images of the tent map subintervals

under the transformation C. If the tent map subintervals are placed along the

x-axis of Figure 3.4, vertical lines are drawn to the curve C and then extended

horizontally to the y-axis, the logistic map subintervals will be produced.

The length of each tent map subinterval of level k (represented by a se-

quence S

...S

of R’s and L’s) is 2

⫺k

. If one of these subintervals is denoted by

], then the length of [C(x

),C(x

)] is

C(x

) ⫺ C(x

) ⫽





(x) dx ⫽



␲

sin

␲

xdx

ⱕ

␲



dx ⫽

␲

⫺ x

) ⫽

␲

k⫹1

. (3.4)

This establishes the upper bound

␲

 2

k⫹1

for the level-k subintervals of the logistic

map G.

To ﬁnish this section, we’ll use the tools we developed in this chapter to

compute the Lyapunov exponent of orbits of the logistic map G. In particular,

we’ll further exploit the correspondence between orbits of the logistic map and

the tent map T.

Consider an orbit 兵x

其 of T that does not contain the point 0. The conjugacy

provides a corresponding orbit C(x

) of the logistic map, as pictured in Figure 3.5.

We’ll use the chain rule (3.3) to get information about the derivatives G



(C(x

)),

and then ﬁnd the Lyapunov exponent. Equation (3.3) implies that



) ⭈⭈⭈T



)

⫽



(C(x

))C



)



k⫹1

)

⭈⭈⭈



(C(x

))C



)



)



(C(x

))C



)



)

⫽ G



(C(x

)) ⭈⭈⭈G



(C(x

))



)



k⫹1

)

. (3.5)

Then

ln |T



) ⭈⭈⭈T



)| ⫽



i⫽1

ln |T



⫽ ln |C



)| ⫺ ln |C



k⫹1

)| ⫹



i⫽1

ln |G



(C(x

))|.

Now we need to divide by k and take the limit. Note that lnC



) k → 0ask →

⬁

since the numerator is constant. Suppose that for the orbit we’re considering, the

120

3.3 CONJUGACY AND THE LOGISTIC M AP

condition

ln |C



k⫹1

→ 0as k →

⬁

(3.6)

is satisﬁed. Under this condition,

lim

k→

⬁



i⫽1

ln |T



)| ⫽ lim

k→

⬁



i⫽1

ln |G



(C(x

))|,

so that the Lyapunov exponents of the corresponding orbits of T and G are

identical.

Condition (3.6) holds, in particular, if the orbit of x never has the sequence

LL in its symbol sequence. For then the orbit never enters the intervals [0, 1 4]

or [7 8, 1]. Since C



(x) ⫽ (

␲

 2) sin

␲

x, we have

␲

sin

␲

ⱕ |C



(x)| ⱕ

␲

for any x in the orbit of x

under T . The natural log of the left-hand side is

therefore a lower bound (away from ⫺

⬁

) for ln |C



k⫹1

)|, and condition (3.6) is

satisﬁed.

More generally, if the orbit of T never has a sequence of m consecutive

L’s in its symbol sequence, then the orbit never enters the intervals [0, 2

⫺m

]or

[1 ⫺ 2

⫺m⫺1

, 1], and the Lyapunov exponent of the corresponding orbit of G will

be again ln 2.

In order to prove that many orbits of G are not periodic or eventually

periodic, we use the fact that the set of eventually periodic orbits of G is a

“countable” set, while the set of all orbits of G is an uncountable set. Readers

unfamiliar with these concepts may want to consult the ﬁrst section of Chapter

4, where the concept of countability is developed.

Theorem 3.13 The logistic map G has chaotic orbits.

Proof: Through the conjugacy with T, we can determine the periodic

points of G; this set is countable. We showed above that all periodic points of

G are sources, and therefore no orbits besides periodic orbits—and eventually

periodic orbits, another countable set—can be asymptotically periodic. Then any

orbit whose corresponding symbol sequence is not eventually periodic, and which

never contains the sequence LL, has Lyapunov exponent ln 2 and is chaotic.

How does what we have proved correspond with what we observe on a

computer screen? Suppose we begin with a typical number between 0 and 1, and

121

C HAOS

0.1

0.2

0.3

0.4

0.5

0.6

0.7

0.8

0.9

0 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1

Figure 3.6 The logistic map.

One hundred iterates are plotted on the x-axis; their images are plotted on the

vertical axis.

compute the resulting orbit of G. If you try this, you will see the iterates ﬁll up

the unit interval. Figure 3.6 shows the ﬁrst 100 iterates of a typical orbit.

We have developed enough mathematics by now to actually prove that

there is a chaotic orbit that travels throughout the entire unit interval. The

chaotic orbits of the proof, for example, never enter the intervals [0, 1 4] or

[7 8, 1]. With just a little extra work we can exhibit an orbit that visits every

neighborhood, no matter how small, of the unit interval [0, 1].

There is a term for a subset A, such as an orbit, that visits every vicinity of

asetB. We make the following deﬁnition.

Deﬁnition 3.14 Let A be a subset of B.ThesetA is dense in B if

arbitrarily close to each point in B there is a point of A. In other words, for each

point x in B and each

⑀

⬎ 0, the neighborhood N

⑀

(x) contains a point in A.

The set of rational numbers is dense in the set of real numbers. To see this,

let x be any real number. We assume that x is a number between 0 and 1, and leave

the general case to the reader. For a given

⑀

⬎ 0, choose n sufﬁciently large that

⫺n

⬍

⑀

. Let a

,...,a

be the ﬁrst n digits of x. Then |x ⫺ .a

...a

| ⬍

⑀

The rational number .a

...a

is in N

⑀

(x).

Orbits are countable by their nature, since the points are in one-to-one

correspondence with the natural numbers. Suppose we plot an orbit on a computer

screen, and observe it ﬁlling up the interval [0, 1]. Of course, speaking precisely,

122

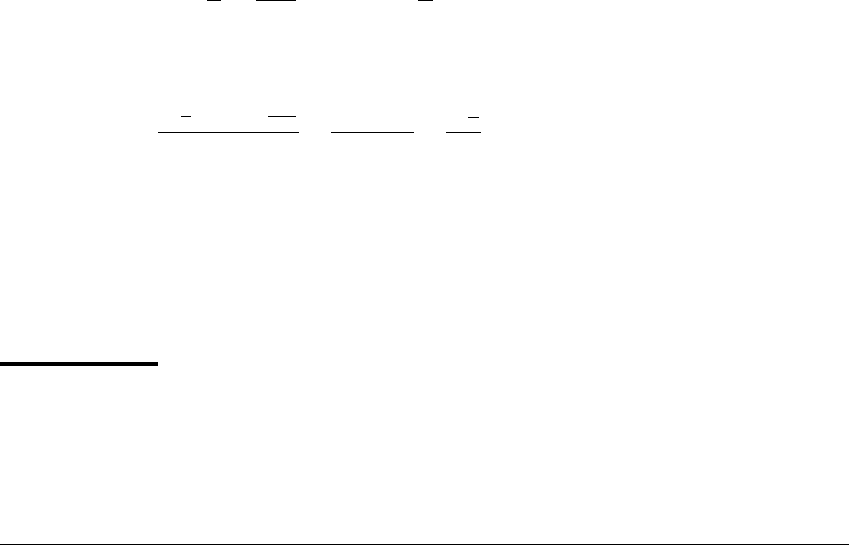
3.3 CONJUGACY AND THE LOGISTIC M AP

it is impossible for one orbit to be the entire interval—the orbit is countable

and the interval is uncountable. But an orbit that leaves no gap unﬁlled in the

interval, that eventually comes arbitrarily close to every point of the interval, is

an orbit that comes as close as is possible to ﬁlling up the interval. Such an orbit

is dense in the interval. Can we ﬁnd a dense chaotic orbit for the logistic map G

in [0, 1]?

Consider the candidate orbit whose itinerary begins with R and L, followed

by all possible pairs of R, L, followed by all triples of R, L,andsoon:

R L RR RL LR LL RRR RRL ...

This orbit is not eventually periodic. If it were, its itinerary would be eventually

periodic. Furthermore, given any interval of length 2

⫺n

represented by a symbol

sequence of n symbols, the orbit, after a sufﬁcient wait, enters that interval. This

is a dense orbit.

Now check the Lyapunov exponent of this dense orbit. If it is positive,

the orbit is a chaotic orbit that is dense in the unit interval. A little checking

veriﬁes that no sequence of m consecutive L’s occurs before the 2

th symbol of

the sequence. Therefore x

does not visit [0, 2

⫺m

]or[1⫺ 2

⫺m⫺1

, 1] until k ⬎ 2

If m is a positive integer, then for k ⬍ 2

␲

sin

␲

m⫹1

ⱕ |C



)| ⱕ

␲

Taking logs and dividing by k preserves the directions of the inequality. For k ⬍ 2

we have

␲

⫹ ln sin

␲

m⫹1

ⱕ

ln |C



ⱕ

␲

As k →

⬁

, both the far left and far right quantities approach zero (use L’Hospital’s

rule for the left side). Thus condition (3.6) is satisﬁed, and the Lyapunov exponent

of the orbit is ln 2.

We have shown that this orbit is not eventually periodic. It is not asymp-

totically periodic because G has no periodic sinks. Since the Lyapunov exponent

of the orbit is ln 2 ⬎ 0, it is a dense chaotic orbit.

E XAMPLE 3.15

While on the subject of conjugacy, there is another example that we have

been using implicitly all along. We will demonstrate using the tent map T.If

⭈⭈⭈is the itinerary of an initial condition x

,thenS

⭈⭈⭈is the itinerary

of T(x

). Because of this, we can deﬁne a map on the set of symbol sequences

123