Alligood K., Sauer T., Yorke J.A. Chaos: An Introduction to Dynamical Systems

Подождите немного. Документ загружается.

T WO-DIMENSIONAL M APS

The ﬁrst lunar swingby occurred on March 30, 1983. A schematic picture

of the satellite trajectory is shown in Color Plate 14. The 4 other near collisions

with the moon are shown in the following Color Plates 15–16. During the ﬁnal

swingby on Dec. 22, 1983, denoted by 5 in the ﬁgure, the satellite passed within

80 miles of the surface of the moon on its way toward the comet. ICE passed

through the tail of the Giacobini-Zinner comet on Sept. 11, 1985, exactly as

planned.

104

C HAPTER T HREE

Chaos

HE CONCEPT of an unstable steady state is familiar in science. It is not possible

in practice to balance a ball on the peak of a mountain, even though the conﬁgu-

ration of the ball perfectly balanced on the peak is a steady state. The problem is

that the trajectory of any initial position of the ball near, but not exactly at, the

steady state, will evolve away from the steady state. We investigated sources and

saddles, which are unstable ﬁxed points of maps, in Chapters 1 and 2.

What eventually happens to the ball placed near the peak? It moves away

from the peak and settles in a valley at a lower altitude. The valley represents a

stable steady state. One type of behavior for an initial condition that begins near

an unstable steady state is to move away and be attracted by a stable steady state,

or perhaps a stable periodic state.

We have seen this behavior in maps of the real line. Consider an initial

condition that is near a source p of a map f. At the beginning of such an orbit,

105

C HAOS

unstable behavior is displayed. Exponential separation means that the distance

between the orbit point and the source increases at an exponential rate. Each

iteration multiplies the distance between them by |f



(p)| ⬎ 1. We say that the

exponential rate of separation is |f



(p)| per iterate. That is, at least at ﬁrst, small

separations grow. After some wandering, the orbit may be attracted to a sink q.

As it nears the sink, the orbit will display convergent behavior—the distance

between the orbit point and the sink will change by the factor |f



(q)| ⬍ 1. As the

orbit nears the attractor, small distances shrink.

It is common to see behavior like this, in which unstable behavior is tran-

sient and gives way eventually to stable behavior in the long run. But there is no

reason that an initial condition starting near a source is forced to end up attracted

to a sink or periodic sink. Perhaps no stable states exist, as in the example of the

logistic map G(x) ⫽ 4x(1 ⫺ x) we discussed in Chapter 1.

A chaotic orbit is one that forever continues to experience the unstable

behavior that an orbit exhibits near a source, but that is not itself ﬁxed or

periodic. It never manages to ﬁnd a sink to be attracted to. At any point of such

an orbit, there are points arbitrarily near that will move away from the point

during further iteration. This sustained irregularity is quantiﬁed by Lyapunov

numbers and Lyapunov exponents. We will deﬁne the Lyapunov number to be

the average per-step divergence rate of nearby points along the orbit, and the

Lyapunov exponent to be the natural logarithm of the Lyapunov number. Chaos

is deﬁned by a Lyapunov exponent greater than zero.

In this chapter, we will study elementary properties of Lyapunov exponents

and exhibit some maps for which they can be explicitly calculated. For example,

we will see that for the logistic map, the Lyapunov exponent of most orbits (but

not all) is ln 2. We’ll also develop a ﬁxed point theorem for detecting ﬁxed and

periodic points, which will be used in Challenge 3 to establish a remarkable fact

called Sharkovskii’s Theorem.

3.1 LYAPUNOV EXPONENTS

We learned in Chapter 1 that for ﬁxed points of discrete dynamical systems,

stability is heavily inﬂuenced by the derivative of the map. For example, if x

is a

ﬁxed point of a one-dimensional map f and f



) ⫽ a ⬎ 1, then the orbit of each

point x near x

will separate from x

at a multiplicative rate of approximately a

per iteration, until the orbit of x moves signiﬁcantly far away from x

. That is, the

distance between f

(x)andf

) ⫽ x

will be magniﬁed by approximately a ⬎ 1

for each iteration of f.

106

3.1 LYAP U NOV E XPONENTS

For a periodic point of period k, we have to look at the derivative of the

kth iterate of the map, which, by the chain rule, is the product of the derivatives

at the k points of the orbit. Suppose this product of derivatives is A ⬎ 1. Then

the orbit of each neighbor x of the periodic point x

separates from x

at a

rate of approximately A after each k iterates. This is a cumulative amount of

separation—it takes k iterations of the map to separate by a distance A. It makes

sense to describe the average multiplicative rate of separation as A

1 k

per iterate.

The term Lyapunov number is introduced to quantify this average multi-

plicative rate of separation of points x very close to x

. (The Lyapunov exponent

will be simply the natural logarithm of the Lyapunov number.) A Lyapunov num-

ber of 2 (or equivalently, a Lyapunov exponent of ln 2) for the orbit of x

will

mean that the distance between the orbit of x

and the orbit of a nearby point x

doubles each iteration, on the average. For a periodic point x

of period k,thisis

the same as saying that

|(f

)



)| ⫽ |f



)||f



)| ⭈⭈⭈|f



)| ⫽ 2

But we want to consider this concept even when x

is not a ﬁxed point or periodic

point. A Lyapunov number of

would mean this distance would be halved on

each iteration, and the orbits of x and x

would move rapidly closer.

The signiﬁcance of the concept of Lyapunov number is that it can be applied

to nonperiodic orbits. A characteristic of chaotic orbits is sensitive dependence

on initial conditions—the eventual separation of the orbits of nearby initial

conditions as the system moves forward in time. In fact, our deﬁnition of a

chaotic orbit is one that does not tend toward periodicity and whose Lyapunov

number is greater than 1.

In order to formally deﬁne Lyapunov number and Lyapunov exponent for a

general orbit, we follow the analogy of the periodic case, and consider the product

of the derivatives at points along the orbit. We begin by restricting our attention

to one-dimensional maps.

Deﬁnition 3.1 Let f be a smooth map of the real line ⺢.TheLyapunov

number L(x

) of the orbit 兵x

,...其 is deﬁned as

L(x

) ⫽ lim

n→

⬁

(|f



)| ...|f



)|)

1 n

if this limit exists. The Lyapunov exponent h(x

)isdeﬁnedas

h(x

) ⫽ lim

n→

⬁

(1 n)[ln |f



)| ⫹⭈⭈⭈⫹ln |f



)|],

if this limit exists. Notice that h exists if and only if L exists and is nonzero, and

ln L ⫽ h.

107

C HAOS

Remark 3.2 Lyapunov numbers and exponents are undeﬁned for some

orbits. In particular, an orbit containing a point x

with f



) ⫽ 0 causes the

Lyapunov exponent to be undeﬁned.

✎ E XERCISE T3.1

Show that if the Lyapunov number of the orbit of x

under the map f is

L, then the Lyapunov number of the orbit of x

under the map f

is L

whether or not x

is periodic.

It follows from the deﬁnition that the Lyapunov number of a ﬁxed point x

for a one-dimensional map f is |f



)|, or equivalently, the Lyapunov exponent

of the orbit is h ⫽ ln |f



)|.Ifx

is a periodic point of period k, then it follows

that the Lyapunov exponent is

h(x

) ⫽

ln |f



)| ⫹⭈⭈⭈⫹ln |f



The point is that for a periodic orbit, the Lyapunov number e

h(x

)

describes the

average local stretching, on a per-iterate basis, near a point on the orbit.

Deﬁnition 3.3 Let f be a smooth map. An orbit 兵x

,... x

,...其 is

called asymptotically periodic if it converges to a periodic orbit as n →

⬁

;this

means that there exists a periodic orbit 兵y

,...,y

,...其 such that

lim

n→

⬁

⫺ y

| ⫽ 0.

Any orbit that is attracted to a sink is asymptotically periodic. The orbit

with initial condition x ⫽ 1 2ofG(x) ⫽ 4x(1 ⫺ x) is also asymptotically periodic,

since after two iterates it coincides with the ﬁxed point x ⫽ 0. The term eventually

periodic is used to describe this extreme case, where the orbit lands precisely on

a periodic orbit.

Theorem 3.4 Let f be a map of the real line ⺢. If the orbit 兵x

,...其

of f satisﬁes f



) ⫽ 0 for all i and is asymptotically periodic to the periodic orbit

兵y

,...其, then the two orbits have identical Lyapunov exponents, assuming both

exist.

Proof: We use the fact that a sequence average converges to the sequence

limit; that is, if s

is an inﬁnite sequence of numbers with lim

n→

⬁

⫽ s,then

lim

n→

⬁



i⫽1

⫽ s.

108

3.2 CHAOTIC O RBITS

Assume k ⫽ 1 to begin with, so that y

is a ﬁxed point. Since lim

n→

⬁

⫽ y

the fact that the derivative f



is a continuous function implies that

lim

n→

⬁



) ⫽ f



( lim

n→

⬁

) ⫽ f



Moreover, since ln |x| is a continuous function for positive x,

lim

n→

⬁

ln |f



)| ⫽ ln | lim

n→

⬁



)| ⫽ ln |f



)|.

This equation gives us the limit of an inﬁnite sequence. Using the fact that the

sequence average converges to the sequence limit, we see that

h(x

) ⫽ lim

n→

⬁



i⫽1

ln |f



)| ⫽ ln |f



)| ⫽ h(y

Now assume that k ⬎ 1, so that y

is not necessarily a ﬁxed point. Then y

is a ﬁxed point for f

, and the orbit of x

is asymptotically periodic under f

to the

orbit of y

. From what we proved above, the Lyapunov exponent of the orbit of

under f

is ln |f



)|. By Exercise T3.1, the Lyapunov exponent of x

under f

ln |(f

)



)| ⫽ h(y

✎ E XERCISE T3.2

Find the Lyapunov exponent shared by most bounded orbits of g(x) ⫽

2.5x(1 ⫺ x). Begin by sketching g(x) and considering the graphical represen-

tation of orbits. What are the possible bounded asymptotic behaviors? Do

all bounded orbits have the same Lyapunov exponents?

➮ COMPUTER EXPERIMENT 3.1

Write a program to calculate the Lyapunov exponent of g

(x) ⫽ ax(1 ⫺ x)

for values of the parameter a between 2 and 4. Graph the results as a function

of a.

3.2 CHAOTIC ORBITS

In Section 3.1 we deﬁned the Lyapunov exponent h of an orbit to be the natural

log of the average per-step stretching of the orbit. We were able to calculate h

109

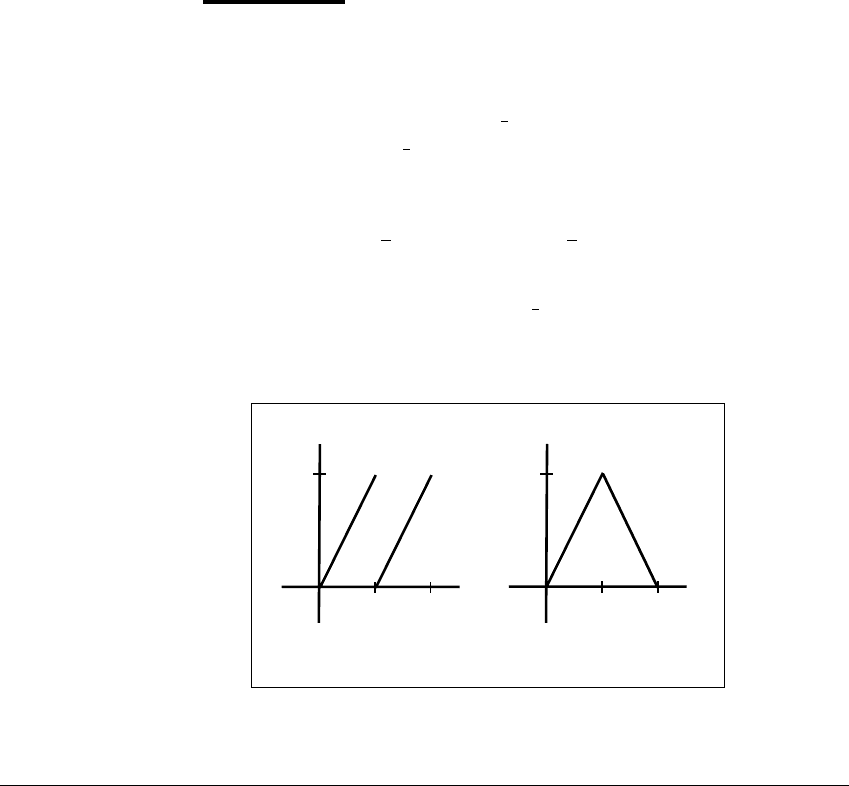
C HAOS

in certain special cases: for a ﬁxed point or periodic orbit we could express h in

terms of derivatives, and orbits converging to a periodic orbit share the same

Lyapunov exponent. More interesting cases involve bounded orbits that are not

asymptotically periodic. When such an orbit has a positive Lyapunov exponent,

it is a chaotic orbit.

Deﬁnition 3.5 Let f be a map of the real line ⺢,andlet兵x

,...其 be

a bounded orbit of f. The orbit is chaotic if

1. 兵x

,...其 is not asymptotically periodic.

2. the Lyapunov exponent h(x

) is greater than zero.

E XAMPLE 3.6

The map f(x) ⫽ 2x (mod 1) on the real line ⺢ exhibits positive Lyapunov

exponents and chaotic orbits. See Figure 3.1(a). The map is not continuous, and

therefore not differentiable, at x ⫽

. We restrict our attention to orbits that

never map to the point

. For these orbits, it is easy to compute the Lyapunov

exponent as

lim

n→

⬁



i⫽1

ln |f



)| ⫽ lim

n→

⬁



i⫽1

ln 2 ⫽ ln 2.

Therefore each orbit that forever avoids

and is not asymptotically periodic is a

chaotic orbit, with Lyapunov exponent ln 2.

1/2 1

(a) (b)

Figure 3.1 Two simple maps with chaotic orbits.

(a) 2x (mod 1) map. (b) The tent map.

110

3.2 CHAOTIC O RBITS

The action of this map on a real number in [0, 1] can be expressed easily if

we consider the binary expansion of the number (see accompanying box). The

map f applied to a number x expressed in a binary expansion chops off the leftmost

bit:

1 5 ⫽ .0011

0011

f(1 5) ⫽ .011

0011

(1 5) ⫽ .110011

(1 5) ⫽ .10011

(1 5) ⫽ .0011

Notice that x ⫽ 1 5 is a period-four orbit of f.

Since the map is so simple in the binary system, we can see immediately

which points in [0, 1] are periodic—they are the points with a repeating binary

B INARY N UMBERS

The binary expansion of a real number x has form

x ⫽ .b

...,

where each b

represents the 2

⫺i

-contribution to x. For example,

⫽ 0 ⭈ 2

⫺1

⫹ 1 ⭈ 2

⫺2

⫹ 0 ⭈ 2

⫺3

⫹ 0 ⭈ 2

⫺4

⫹⭈⭈⭈ ⫽ .010

and

⫽ 0 ⭈ 2

⫺1

⫹ 0 ⭈ 2

⫺2

⫹ 1 ⭈ 2

⫺3

⫹ 1 ⭈ 2

⫺4

⫹⭈⭈⭈ ⫽ .0011

where the overbar means inﬁnite repetition.

To compute the binary expansion of a number between 0 and 1,

multiply the number by 2 (using the decimal system if that’s easiest

for you) and take the integer part (if any) as the ﬁrst binary digit (bit).

Repeat the process, multiply the remainder by 2, and take the integer

part as the second bit, and so on. Actually, we are applying the 2x

(mod 1) map, recording a 1 bit when the mod truncation is necessary,

and a 0 bit if not.

111

C HAOS

expansion, like x ⫽ 1 5. The eventually periodic points are those with an even-

tually repeating binary expansion, like x ⫽ 1 4 ⫽ .01

0orx ⫽ 1 10 ⫽ .00011.

The only way to have an asymptotically repeating expansion is for it to be even-

tually repeating. We conclude that any number in [0, 1] whose binary expansion

is not eventually repeating represents a chaotic orbit. These are exactly the initial

points that are not rational.

E XAMPLE 3.7

Let f(x) ⫽ (x ⫹ q)(mod1),whereq is an irrational number. Although f is

not continuous as a map of the unit interval, when viewed as a map of the circle

(by gluing together the unit interval at the ends 0 and 1), it rotates each point

through a ﬁxed angle and so is continuous.

There are no periodic orbits, and therefore no asymptotically periodic orbits.

Each orbit wanders densely throughout the circle, and yet no orbit is chaotic. The

Lyapunov exponent of any orbit is 0. A bounded orbit that is not asymptotically

periodic and that does not exhibit sensitive dependence on initial conditions is

called quasiperiodic.

✎ E XERCISE T3.3

Let f (x) ⫽ (x ⫹ q)(mod1),whereq is irrational. Verify that f has no

periodic orbits and that the Lyapunov exponent of each orbit is 0.

In the remainder of this section we establish the fact that the tent map has

inﬁnitely many chaotic orbits. Since the Lyapunov exponent of each orbit for

which it is deﬁned is ln 2, proving chaos reduces to checking for the absence of

asymptotic periodicity, which we do through itineraries.

E XAMPLE 3.8

The tent map

T(x) ⫽



2x if x ⱕ 1 2

2(1 ⫺ x)if1 2 ⱕ x

on the unit interval [0, 1] also exhibits positive Lyapunov exponents. The tent

map is sketched in Figure 3.1(b). Notice the similarity of its shape to that of the

logistic map. It is the logistic map “with a corner”.

In analogy with the treatment of the logistic map, we set L ⫽ [0, 1 2]

and R ⫽ [1 2, 1]. The transition graph of T is shown in Figure 3.2(a), and the

112

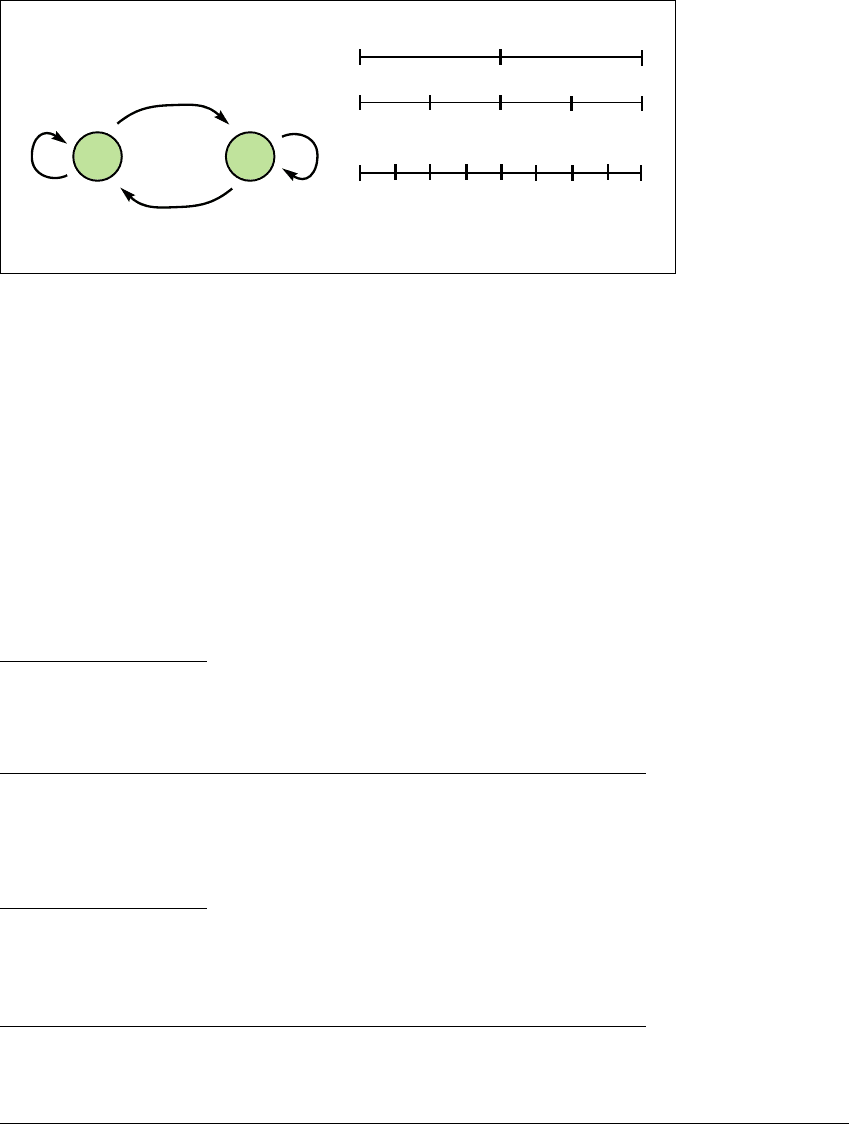
3.2 CHAOTIC O RBITS

LR RR

LLL

LLR

LRR LRL

RRL

RRR

RLR RLL

(a) (b)

Figure 3.2 Tent map symbolic dynamics.

(a) Transition graph and (b) schematic iteneraries for the tent map T.

itineraries of T are shown in Figure 3.2(b). Recall that the subinterval RRL, for

example, denotes the set of points x that satisfy x is in R, T(x)isinR,andT

(x)

is in L.

Because of the uniform shape of T(x), there is a uniformity in the lengths

of subintervals having a given ﬁnite itinerary. The set of points with itinerary

...S

has length 2

⫺k

, independent of the choice of symbols. Figures 3.2(a) and

(b) are identical to the corresponding ﬁgures in Chapter 1 for the logistic map

G(x) ⫽ 4x(1 ⫺ x), except that for the tent map the level-k itinerary subintervals

are all of equal length.

✎ E XERCISE T3.4

Explain why each inﬁnite itinerary of the tent map T represents the orbit

of exactly one point in [0, 1].

We conclude that if the orbits that contain x ⫽ 1 2 are ignored, then

the orbits of T are in one-to-one correspondence with inﬁnite sequences of two

symbols.

✎ E XERCISE T3.5

Explain why an eventually periodic orbit must have an eventually repeating

itinerary.

Using the correspondence between orbits of T and their itineraries, chaos

can be shown to exist in the tent map.

113