Alligood K., Sauer T., Yorke J.A. Chaos: An Introduction to Dynamical Systems

Подождите немного. Документ загружается.

C HAOS

[0,1]

S S

n+1

=T(x

)

LRRRLR...

RRRLR...

(a) (b)

Figure 3.7 Tent map conjugacy.

The map T is conjugate to the shift map on the two symbols L and R.(a)The

conjugacy betwen T and the shift s. (b) Schematic view of the action of the

conjugacy map C.

whose dynamical properties mirror those of T. The translation between them can

be thought of as a conjugacy.

Deﬁnition 3.16 The set S of all inﬁnite itineraries of a map is called the

symbol space for the map. The shift map s is deﬁned on the symbol space S as

follows:

s(S

...) ⫽ S

....

The shift map chops the leftmost symbol, which is the analogue on the itinerary

of iterating the map on the point.

Figure 3.7 is an analogue of Figure 3.5, but for the conjugacy of the tent

map with the shift map. The conjugacy C moves a point in [0, 1] to its itinerary.

An orbit of T in [0, 1] has a corresponding “orbit” in symbol space where the

dynamics consist of chopping off one symbol from the left end of the inﬁnite

sequence each iterate.

3.4 TRANSITION GRAPHS AND FIXED POINTS

Imagine that a 12-inch plastic ruler is melted and stretched lengthwise, beyond

its true length, and then laid down to completely cover a true 12-inch ruler. We’ll

allow the stretched ruler to be laid in the same orientation as the true ruler, or

124

3.4 TRANSITION G RAPHS AND F IXED P OINTS

in the reversed orientation. In either case there must be a real number between

0 and 12 for which the rulers line up exactly. This fact is expressed in Theorem

3.17.

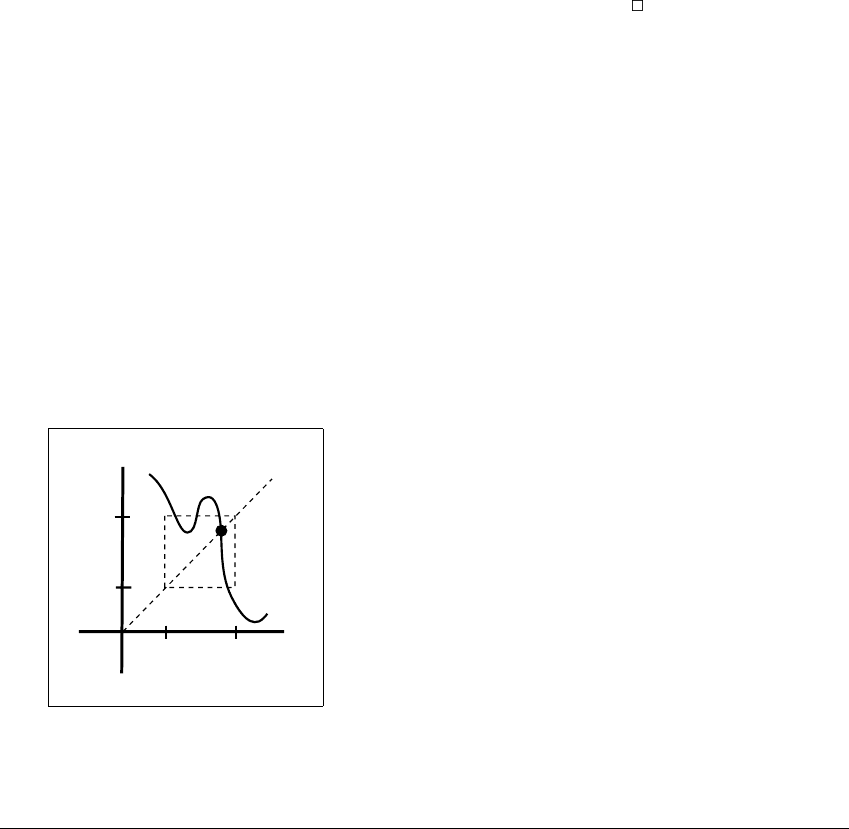
Theorem 3.17 [Fixed-Point Theorem] Let f be a continuous map of the real

line, and let I ⫽ [a, b] be an interval such that f(I) 傶 I. Then f has a ﬁxed point in I.

Proof: Since f(I) contains numbers as large as b and as small as a,there

is a point in I for which the function f(x) ⫺ x ⱖ 0, and a point in I for which

f(x) ⫺ x ⱕ 0. By the Intermediate Value Theorem, there is a point c in I such

that f(c) ⫺ c ⫽ 0.

This Fixed-Point Theorem says that if the image of an interval I covers the

interval I itself, then I contains a ﬁxed point. Since periodic points of a map are

ﬁxed points of higher iterates of the map, the same theorem can be exploited

to prove the existence of periodic points. Assume that I

,...,I

are closed

intervals, and that f(I

) 傶 I

,f(I

) 傶 I

,...,f(I

n⫺1

) 傶 I

,andthatf(I

) 傶 I

In that case we can conclude that f

) 傶 I

,andthatf

has a ﬁxed point in I

It corresponds to a periodic orbit of f (of period n or possibly less), that moves

through the intervals I

in succession before returning to I

Our goal in this section is to use this theorem in conjunction with the

itineraries developed in the previous section to establish the existence of large

quantities of periodic orbits. Recall the deﬁnition of transition graphs in Chapter

1. We begin with a partition of the interval I of interest, which is a collection of

Figure 3.8 The content of Theorem 3.17:

If a function f maps the interval [a, b] across itself, as in the picture, then f must

have a ﬁxed point in that interval.

125

C HAOS

subintervals that are pairwise disjoint except at the endpoints, whose union is I.

The arrows in a transition graph are drawn subject to the following rule.

C OVERING R ULE FOR T RANSITION G RAPHS

An arrow is drawn from A to B in a transition graph if and only if the

image f(A) contains the subinterval B.

Figure 3.2(a) shows a transition graph for the tent map. The set 兵L, R其 is an

example of a partition of the unit interval.

The covering rule has a very interesting consequence for paths in the graph

that are allowed by the arrows. First note that set containment is preserved by

amap.Thatis,ifA 傺 B,thenf(A) 傺 f(B). The covering rule means that if

A → B → C is an allowed path in the transition graph, then f(A) 傻 B and

f(B) 傻 C.Sincef

(A) 傻 f(B), it follows that f

(A) covers C. More generally, if

the sequence S

...S

k⫹1

is an allowable path, then f

) 傻 S

k⫹1

Now we can see how Theorem 3.17, the Fixed-Point Theorem, can be

used to establish the existence of periodic orbits. Assume that 兵S

,...,S

其 is a

partition. If the transition graph of f allows a sequence of symbols that returns to

the same symbol, such as S

...S

,thenf

) 傶 S

,sothatf

has a ﬁxed point

lying in S

. Of course, the periodic orbit we have found may not be a period-k

orbit of f—its period could be an integer that divides evenly into k. We can sum

this up as a consequence of the Fixed-Point Theorem.

Corollary 3.18 Assume that S

...S

is a path in the transition graph

of a map f. Then the subinterval denoted by S

⭈⭈⭈S

contains a ﬁxed point

of f

For the logistic map G(x) ⫽ 4x(1 ⫺ x), Corollary 3.18 can be used as another

way to prove the existence of periodic orbits of every period. For example, the

transition graph of G in Chapter 1 shows that there is an orbit with sequence

beginning LRLRRLL. We can immediately conclude that there is a ﬁxed point

of G

belonging to the subinterval L. What can we say about the corresponding

periodic orbit of G? From what we know so far, it could be an orbit of period 1,

2, 3, or 6. But we know a little more from the itinerary. The orbit cannot be a

ﬁxed point of G; according to the itinerary, it moves between L and R,andthe

126

3.4 TRANSITION G RAPHS AND F IXED P OINTS

only point in both L and R is x ⫽ 1 2, which does not have this itinerary. If

the corresponding orbit of G were a period-two orbit, then the symbols would be

forced to repeat with period two (for example, as LRLRLRL). So the orbit is not a

period-two orbit of G, nor period-3, by similar reasoning. So there is a period-6

orbit for G in L. An argument of this type can be used to prove the existence of a

periodic orbit for any period.

✎ E XERCISE T3.9

(a) Find a scheme to provide, for any positive integer n, a sequence

...S

n⫹1

of the symbols L and R such that S

⫽ S

n⫹1

,andsuchthat

the sequence S

...S

is not the juxtaposition of identical subsequences of

shorter length. (b) Prove that the logistic map G has a periodic orbit for

each integer period.

✎ E XERCISE T3.10

Period-three implies all periods! Consider the period-three map of

Chapter 1, shown in Figure 1.14. (a) Find itineraries that obey the transition

graph of the period-three map for any period, which are not periodic for

any lower period. (b) Prove that the period-three map has periodic orbits

for each positive integer period.

Exercise T3.10 applies only to the particular map of the type drawn in

Figure 1.14 of Chapter 1. This is because we veriﬁed the transition graph only for

this particular case. However, the fact is that the existence of a period-three orbit

for a continuous map implies the existence of points of every period. An even

more general result, called Sharkovskii’s Theorem, is the subject of Challenge 3

at the end of this chapter.

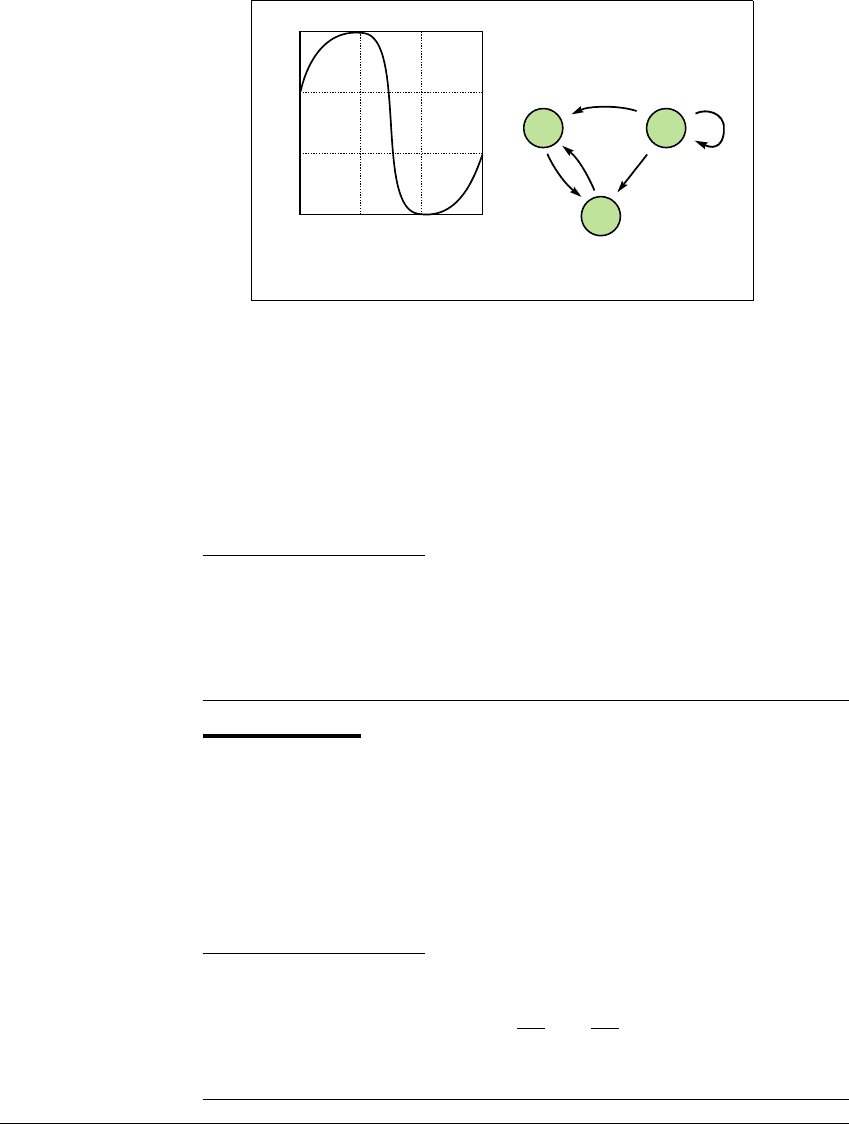
E XAMPLE 3.19

Consider the map f graphed in Figure 3.9. The three subintervals I, J,and

K form a partition. The transition graph is shown in Figure 3.9(b). From the

transition graph we can write down some valid symbol sequences. For example,

J, meaning an inﬁnite sequence of the symbol J, is valid according to the ﬁgure.

The symbol sequences

I and K are not valid. In fact, we can conclude from the

ﬁgure that

J, IK, KI, and each of the latter two preceded by a ﬁnite number of J’s,

are the only valid sequences.

127

C HAOS

J K

(a) (b)

Figure 3.9 Example 3.19.

(a) The subintervals I, J,andK form a partition for the map shown. (b) Transition

graph.

So far we are guaranteed a ﬁxed point (because JJ is a path in the transition

graph) and a period-two orbit (because IKI is legal, and because the corresponding

ﬁxed point of f

clearly cannot be a ﬁxed point of f).

✎ E XERCISE T3.11

(a) Prove that f in Figure 3.9(a) has a ﬁxed point and no other periodic

points whose period is an odd number. (b) Prove that every periodic orbit

has period 1 or 2. Where are they?

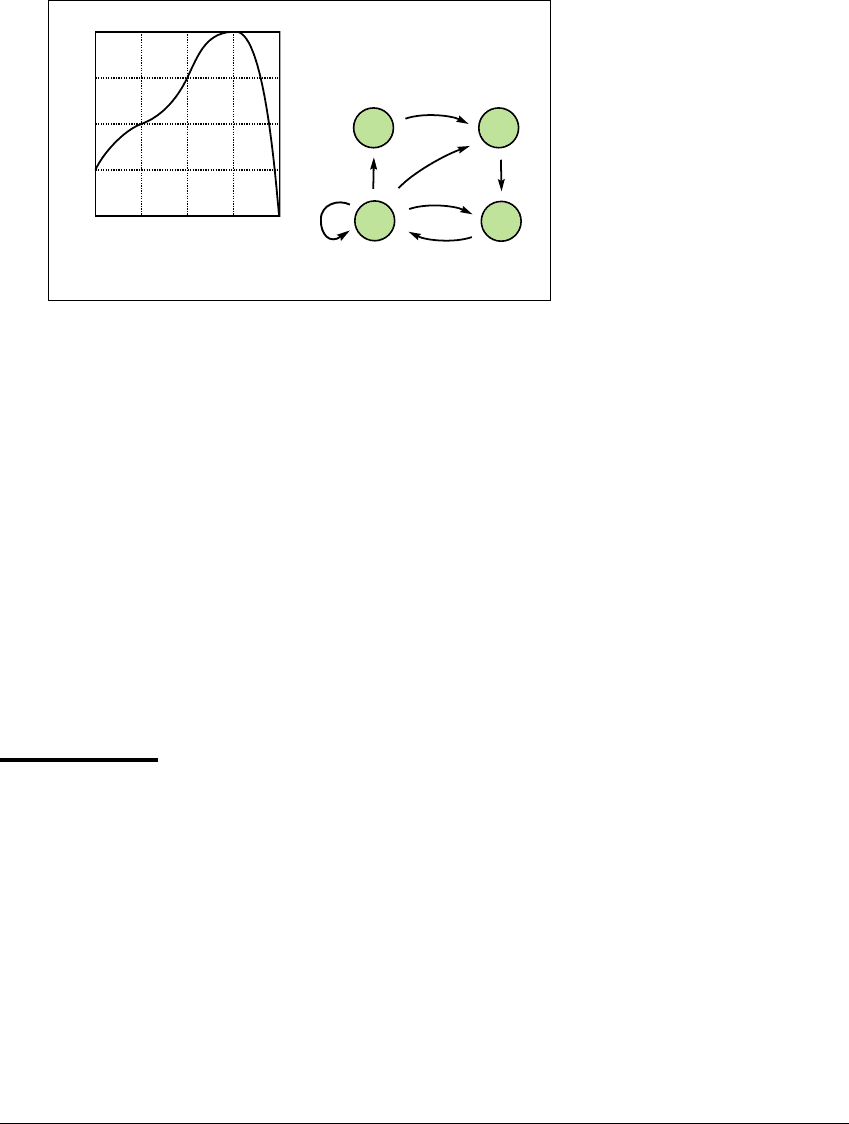
E XAMPLE 3.20

Consider the map f graphed in Figure 3.10(a). There are four subintervals

I, J, K,andL that form a partition. The transition graph is shown in Figure 3.10(b).

This time, notice that the sequence JKLJ is possible so the map f has a period-three

orbit. Note also that JKL ...LJ is possible. This implies that f has periodic orbits

of all periods.

✎ E XERCISE T3.12

List all periodic sequences for periodic orbits of f in Figure 3.10 of period

lessthanorequalto5.Note:

JKL and KLJ are not distinct since they

represent the same orbit.

128

3.5 BASINS OF ATTRACTION

I J

(a) (b)

Figure 3.10 A map with a four-piece partition.

(a) The subintervals I, J, K, L form a covering partition for the map shown. (b) Tran-

sition graph for I, J, K, L.

3.5 BASINS OF ATTRACTION

The concept of “stable manifold” was introduced in Chapter 2 to refer to the set

of points whose forward orbits converge to a ﬁxed or periodic point. In this section

we investigate more closely the set of points whose orbits converge to an attracting

ﬁxed point or periodic point, called the “basin of attraction” or just “basin” of the

sink, and prove a useful theorem about attractors for one-dimensional maps.

Deﬁnition 3.21 Let f beamapon⺢

and let p be an attracting ﬁxed

point or periodic point for f.Thebasin of attraction of p, or just basin of p, is

the set of points x such that | f

(x) ⫺ f

(p) |→ 0, as k →

⬁

E XAMPLE 3.22

For the map f(x) ⫽ ax on ⺢

with |a| ⬍ 1, zero is a ﬁxed point sink whose

basin is the entire real line. More generally, if f is a linear map on ⺢

whose matrix

representation has distinct eigenvalues that are less than one in magnitude, then

the origin is a ﬁxed sink whose basin is ⺢

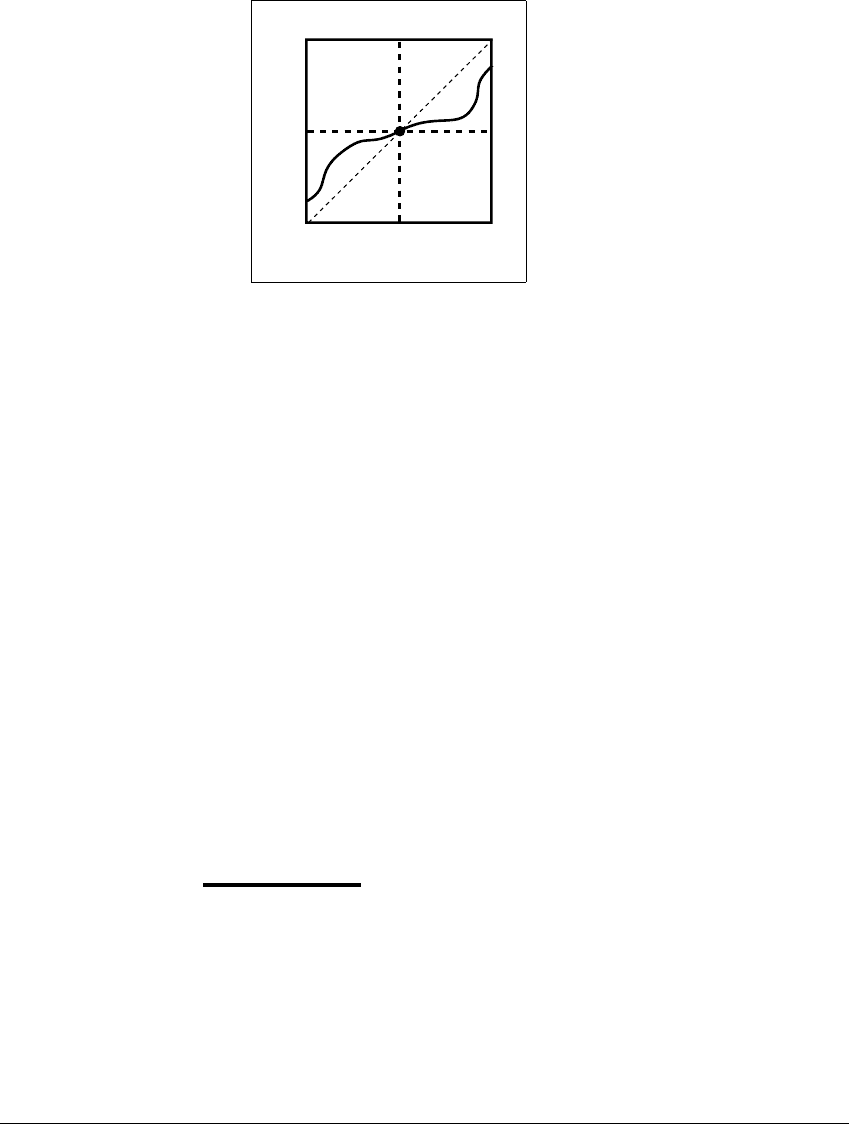
Theorem 3.23 is useful for ﬁnding basins for sinks of some simple maps

on ⺢

Theorem 3.23 Let f be a continuous map on ⺢

(1) If f(b) ⫽ bandx⬍ f(x) ⬍ bforallxin[a, b),thenf

(a) → b.

(2) If f(b) ⫽ bandb⬍ f(x) ⬍ xforallxin(b, c],thenf

129

C HAOS

a b

Figure 3.11 Illustration of Theorem 3.23.

The sink shown at x ⫽ b attracts all initial values in the interval [a, c].

The content of this theorem is expressed in Figure 3.11, which shows the

graph of a map f on ⺢

. Part (1) of the theorem says that the basin of b contains

all initial values to the left of b, and part (2) says it contains all initial values to

the right of b.

Proof: We establish (1), and leave (2) to the reader. Let x

⫽ a, x

i⫹1

⫽

f(x

) for i ⱖ 0. If x 僆 [a, b), then f(x) 僆 [a, b). In fact, a ⱕ x ⬍ f(x) ⬍ b.Thusall

僆 [a, b). Further, the x

are strictly increasing and bounded above by b.Since

increasing bounded sequences must converge, x

→ x

ⴱ

for some x

ⴱ

僆 [a, b]. Taking

limits, we have

ⴱ

⫽ lim

i→

⬁

i⫹1

⫽ lim

i→

⬁

f(x

) ⫽ f(x

ⴱ

by the continuity of f.Sinceb is the only ﬁxed point in [a, b], x

ⴱ

⫽ b.

E XAMPLE 3.24

Consider the map f(x) ⫽ (4

␲

) arctan x on ⺢

. See Figure 3.12. This map

has three ﬁxed points: ⫺1, 0, 1. Using Theorem 1.9 of Chapter 1, it is easy to

check that ⫺1 and 1 are sinks, and that 0 is a source. It follows from Theorem

3.23 that the basin of the ﬁxed point 1 is the set of all positive numbers. The

basin of 1 is colored gray in Figure 3.12. Likewise, the basin of ⫺1isthesetofall

negative numbers, and is shown in black.

130

3.5 BASINS OF ATTRACTION

-1

Figure 3.12 The map

ⴝ

(

) ⴝ (4

␲

)arctan

The basin of the sink ⫺1 is shown in black, and the basin of 1 is in gray.

E XAMPLE 3.25

Consider the logistic map f(x) ⫽ ax(1 ⫺ x), shown in Figure 1.5 of Chap-

ter 1. If 0 ⬍ a ⬍ 1, there is a single attracting ﬁxed point x ⫽ 0. Theorem 3.23

says that the interval ((a ⫺ 1) a, 1] lies in the basin of x ⫽ 0. From graphical

representation of orbits, it is clear that in addition, the interval [1, 1 a)iscon-

tained in the basin of 0. It is also clear that the intervals (⫺

⬁

, (a ⫺ 1) a)and

(1 a,

⬁

) consist of initial conditions that diverge to inﬁnity. We could say that

these points belong to the “basin of inﬁnity”.

If 1 ⬍ a ⬍ 2, the sink has moved to the right from 0 to (a ⫺ 1) a.Theorem

3.23 and some graphical analysis implies that the basin of the sink (a ⫺ 1) a is

(0, 1).

E XAMPLE 3.26

Consider the map of the plane deﬁned by

f(r,

␪

) ⫽ (r

␪

⫺ sin

␪

where r ⱖ 0and0ⱕ

␪

⬍ 2

␲

are polar coordinates. There are three ﬁxed points

(the origin, (r,

␪

) ⫽ (1, 0) and (1,

␲

)). The origin and inﬁnity are attractors. Ev-

ery initial condition inside the unit circle tends toward the origin upon iteration,

and every point outside the unit circle tends toward inﬁnity. The basins of these

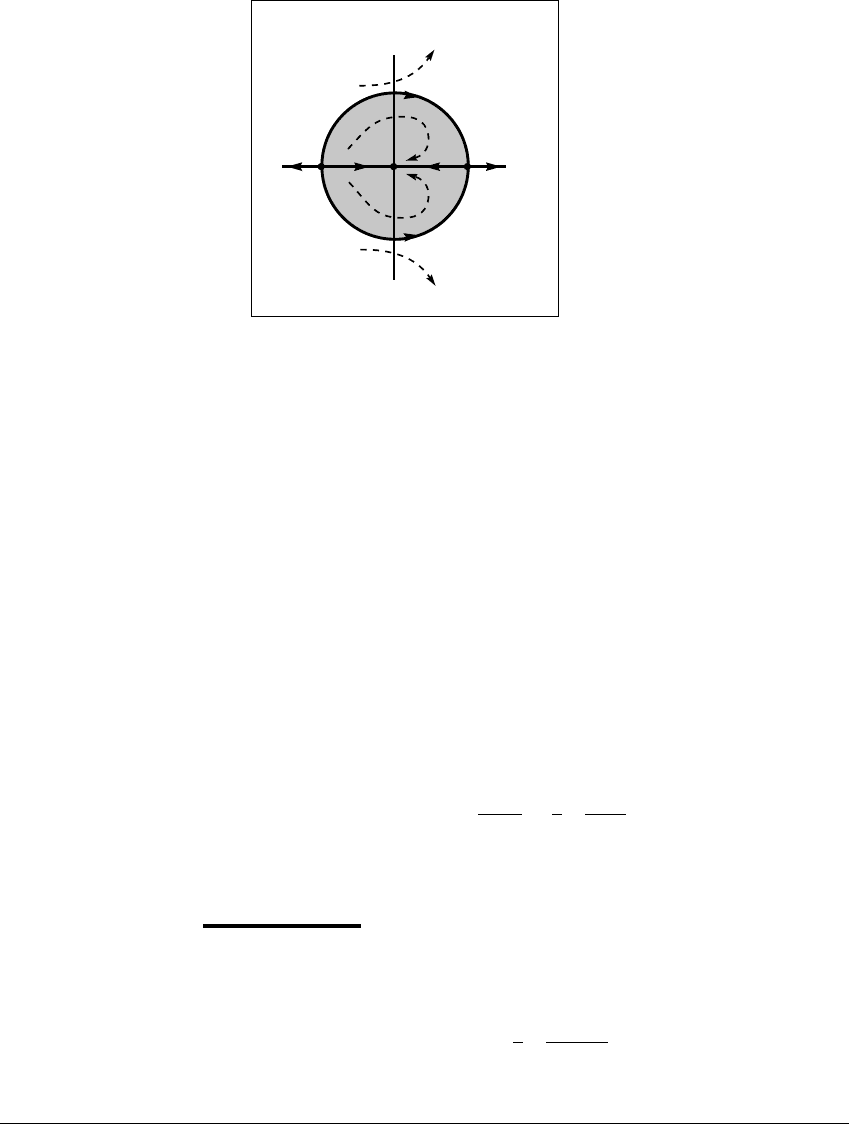
two attractors are shown in gray and white, respectively, in Figure 3.13.

The dynamics on the dividing circle are also rather tame; there is a ﬁxed

point at (r,

␪

) ⫽ (1, 0) to which all points on the circle tend, except for the ﬁxed

point (r,

␪

) ⫽ (1,

␲

). The basin boundary itself is unstable, in the sense that

points near it are repelled, except for points precisely on the boundary.

131

C HAOS

Figure 3.13 The map of Example 3.26.

The gray region is the basin of the origin. The white region is the basin of inﬁnity.

One of the most interesting features of nonlinear maps is their ability to

have more than one attractor. The arctan map of Example 3.24 has coexisting

sinks. However, the diagram of attractors of the logistic family of maps in Figure

1.6 of Chapter 1 appears not to have coexisting attractors—for each value of the

parameter a, only one attractor is visible. This section is devoted to proving that

this observation is correct. It is useful to introduce the Schwarzian derivative for

this purpose. Theorem 3.29 states that maps like the logistic map, with negative

Schwarzian and ﬁnite basins, can have at most one attracting periodic orbit. The

remainder of this section pertains only to one-dimensional maps.

Deﬁnition 3.27 Let f be a smooth map on ⺢

.TheSchwarzian deriva-

tive of f is deﬁned by

S(f)(x) ⫽



(x)



(x)

⫺





(x)



(x)



We will say that a map has negative Schwarzian if S(f)(x) is negative whenever



(x) ⫽ 0.

E XAMPLE 3.28

Check that g(x) ⫽ ax(1 ⫺ x) has Schwarzian derivative

S(g )(x) ⫽⫺



⫺2a

a ⫺ 2ax



and therefore has negative Schwarzian.

132

3.5 BASINS OF ATTRACTION

✎ E XERCISE T3.13

Show that if f and g have negative Schwarzian, then f ◦ g has negative

Schwarzian. Therefore if f has negative Schwarzian, so does each iterate f

of f .

In the following theorem, we say that a ﬁxed point or periodic point p has

an “inﬁnite basin” if the basin of p contains an interval of inﬁnite length. Recall

that a “critical point” of a map f is a point c such that f



Theorem 3.29 If the map f on ⺢

has negative Schwarzian, and if p is a ﬁxed

point or a periodic point for f, then either:

1. p has an inﬁnite basin; or

2. there is a critical point of f in the basin of p; or

3. p is a source.

Proof: We will assume that p is not a source nor a sink with an inﬁnite

basin, and prove that there is a critical point c of f in the basin of p.

First consider the simpler case f(p) ⫽ p, f



(p) ⱖ 0. If p is itself a critical

point of f, then we are done. Otherwise, 0 ⬍ f



(p) ⱕ 1, since p is not a source.

Note that f



(x) cannot be constant in a neighborhood of p, since on that interval



⫽ f



⫽ 0 would imply S(f) ⫽ 0.

It is clear from Theorem 3.23 that since p does not have an inﬁnite basin, we

can conclude that either f has a critical point in the basin of p, in which case we are

done, or there exists an interval (a,b) in the basin containing p such that f



(a) ⱖ 1

and f



(b) ⱖ 1. Since f



(p) ⱕ 1, there is a local minimum m for f



in the basin

of p.Notethatf



(m) ⫽ 0andf



(m) ⬎ 0, so that negative Schwarzian implies



(m) ⬍ 0. By the Intermediate Value Theorem there is a number c between p

and m such that f



and a ⬍ c ⬍ b, we have found a critical point in the basin of p.

We can now describe the general case, in which p is a periodic point of

period k.Sincep is not a source orbit nor a sink orbit with inﬁnite basin for the map

f, the same is true for the ﬁxed point p of the map f

. Since (f

)



(p) ⫽ (f

)



(p)

we know that 0 ⱕ (f

)



(p) ⱕ 1. If (f

)



(p) ⫽ 0, then there is a critical point in

the orbit of p (check this), and therefore in the basin, and we are done. We are

left with the case 0 ⬍ (f

)



(p) ⱕ 1, and we can apply the above argument to f

since by Exercise T3.13, it also has negative Schwarzian. We conclude that f

has a critical point in the basin of p,andsof has also.

133