Alligood K., Sauer T., Yorke J.A. Chaos: An Introduction to Dynamical Systems

Подождите немного. Документ загружается.

4.1 CANTOR S ETS

Note that every point in the Cantor set with a terminating ternary expansion is

identiﬁed with one of the natural numbers. By analogy, the subset of the Cantor

set consisting of left-hand endpoints is also a countable set. Next we will show

that the entire Cantor set is not a countable set.

✎ E XERCISE T4.2

Characterize the set of left-hand endpoints of the removed intervals for

the Cantor set in terms of ternary expansions.

Cantor invented a technique for showing that certain sets are uncountable.

A set is uncountable if every attempt to list all the elements must miss some of

the set. We will demonstrate his technique by using it to show that the set K is

uncountable (even though the subset of elements that have a terminating ternary

expansion is countable).

Any list of numbers in K can be written

Integer Number in

ⴥ

1 r

⫽ .a

...

2 r

⫽ .a

...

3 r

⫽ .a

...

n r

⫽ .a

...

where each entry a

is a 0 or 2. Deﬁne the number r ⫽ .b

...in the following

way. Choose its ﬁrst digit b

to be 0 if a

is2and2ifa

is 0. In general, choose its

nth digit b

to be a 0 or 2 but different from a

. Notice that the number r we have

deﬁned cannot be in the list—in particular, it can’t be the seventh number on the

list, for the seventh digit b

does not agree with a

. Every element in the list has

at least one digit that doesn’t match. We know that each element of the Cantor

set has exactly one representation using 0 and 2. We conclude that no single list

can contain all the elements of K. Therefore the middle-third Cantor set is an

uncountable set. With similar reasoning, using the symbols 0 and 1 instead of 0

and 2, we can show that the unit interval [0, 1] is an uncountable set.

155

F RACTALS

4.2 PROBABILISTIC CONSTRUCTIONS

FRACTALS

In the ﬁrst section we described a deterministic process which produced the

middle-third Cantor set. Next we devise a probabilistic process which reproduces

this set.

E XAMPLE 4.3

Play the following game. Start with any point in the unit interval [0, 1]

and ﬂip a coin. If the coin comes up heads, move the point two-thirds of the

way towards 1. If tails, move the point two-thirds of the way to 0. Plot the point

that results. Then repeat the process. Flip the coin again and move two-thirds of

the way from the new point to 1 (if heads) or to 0 (if tails). Plot the result and

continue.

Aside from the ﬁrst few points plotted, the points that are plotted appear to

ﬁll out a middle-third Cantor set. More precisely, the Cantor set is an attractor for

the probabilistic process described, and the points plotted in the game approach

the attractor at an exponential rate.

The reason for this is clear from the following thought experiment. Start

with a homogeneous distribution, or cloud, of points along the interval [0, 1].

The cloud represents all potential initial points. Now consider the two possible

outcomes of ﬂipping the coin. Since there are two equally likely outcomes, it is

fair to imagine half of the points of the cloud, randomly chosen, moving two

thirds of the way to 0, and the other half moving two-thirds of the way to 1. After

this, half of the cloud lies in the left one-third of the unit interval and the other

half lies in the right one-third. After one hypothetical ﬂip of the coin, there are

two clouds of points covering K

⫽ [0, 1 3] 傼 [2 3, 1] with a gap in between.

After the second ﬂip, there are four clouds of points ﬁlling up K

. Reasoning

in this way, we see that an orbit that is generated randomly by coin ﬂips will stay

within the clouds we have described, and in the limit, approach the middle-third

Cantor set. In fact, the reader should check that after k ﬂips of the coin, the

randomly-generated orbit must lie within 1 (3

6) of a point of the Cantor set.

Verify further that the Cantor set is invariant under the game: that is, if a point in

the Cantor set is moved two-thirds of the way either to 0 or 1, then the resulting

point is still in the Cantor set.

The game we have described is an example of a more general concept we

call an iterated function system.

156

4.2 PROBABILISTIC C ONSTRUCTIONS OF F RACTALS

Deﬁnition 4.4 An iterated function system on ⺢

is a collection

兵f

,...,f

其 of maps on ⺢

together with positive numbers p

,...,p

(to be

treated as probabilities) which add up to one.

Given an iterated function system, an orbit is generated as follows. Begin

with a point in ⺢

, and choose a map from the system with which to iterate the

point. The map is chosen randomly according to the speciﬁed probabilities, thus

map f

is chosen with probability p

. Use the randomly chosen map to iterate the

point, and then repeat the process.

For certain kinds of maps f

, the iterated function system will generate a

fractal. For example, assume that each f

is an afﬁne contraction map on ⺢

deﬁned to be the sum of a linear contraction and a constant. This means that

(v) ⫽ L

v ⫹ c

where L

is an m ⫻ m matrix with eigenvalues smaller than one

in magnitude. Then for almost every initial condition, the orbit generated will

converge exponentially fast to the same bounded set.

Example 4.3 is an iterated function system on ⺢

.Letf

(x) ⫽ x 3and

(x) ⫽ (2 ⫹ x) 3, with associated probabilities p

⫽ p

⫽ 1 2. Check that both

maps are afﬁne contraction maps and have unique sinks at 0 and 1, respectively.

Recently, iterated function systems have proved to be useful tools in data

and image compression. See (Barnsley, 1988) for an introduction to this subject.

➮ COMPUTER EXPERIMENT 4.1

The experiments in this chapter require the ability to plot graphics on a

computer screen or printer. Deﬁne an iterated function system by

(x, y) ⫽ (x 2,y 2), f

(x, y) ⫽ ((1 ⫹ x) 2,y 2), f

(x, y) ⫽ (x 2, (1 ⫹ y) 2)

with probabilities p

⫽ p

⫽ 1 3. Begin with any point in the unit square

[0, 1] ⫻ [0, 1] and use a random number generator or three-headed coin to gen-

erate an orbit. Plot the attractor of the iterated function system. This fractal is

revisited in Exercise 4.9.

E XAMPLE 4.5

Consider the skinny baker map on ⺢

shown in Figure 4.3. This map

exhibits the properties of stretching in one direction and shrinking in the other

157

F RACTALS

1/3 2/3

1/2

0 1

(a)

1/3 2/3

(b) (c)

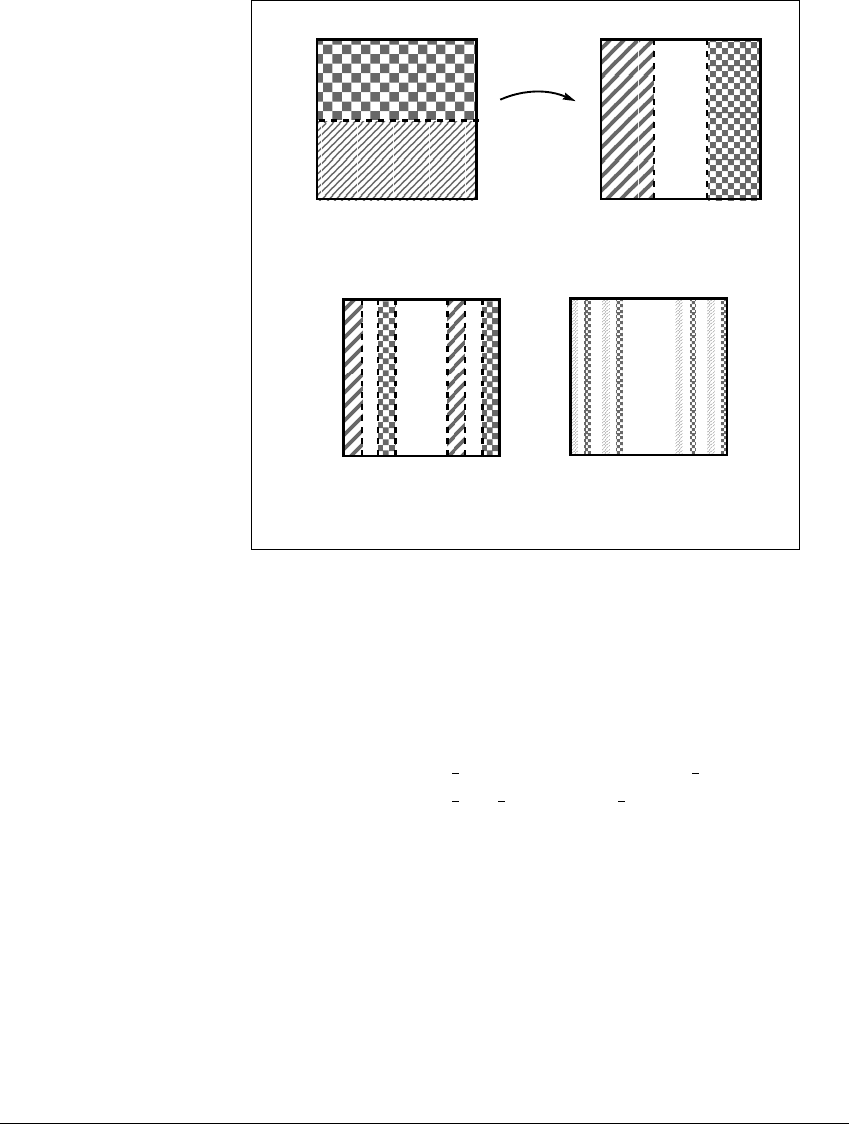
Figure 4.3 Deﬁnition of the skinny baker map.

(a) The top half maps to the right strip. The bottom half maps to the left strip.

(b) The second and (c) third iterate of the map. In the limit, the invariant set is a

Cantor middle-third set of vertical lines.

that are typical for chaotic two-dimensional maps. The equations of the map are

B(x, y) ⫽



(

x, 2y)if0ⱕ y ⱕ

(

x ⫹

, 2y ⫺ 1) if

⬍ y ⱕ 1.

The map is discontinuous, since points (x, y)wherey is less than 1 2 are mapped

to the left side of the unit square, while points with y greater than 1 2 are mapped

to the right. So there are pairs of points on either side of the line y ⫽ 1 2that

are arbitrarily close but are mapped at least 1 3unitapart.

After one application of the map, the image of the unit square lies in the

left one-third and right one-third of the square. After two iterations, the image

of the unit square is the union of four strips, as shown in Figure 4.3(b). The set

to which all points of the unit square are eventually attracted is a Cantor set of

line segments. In fact, there is a close relationship between the skinny baker map

and the probabilistic game of Example 4.3. Sending the bottom half of the square

158

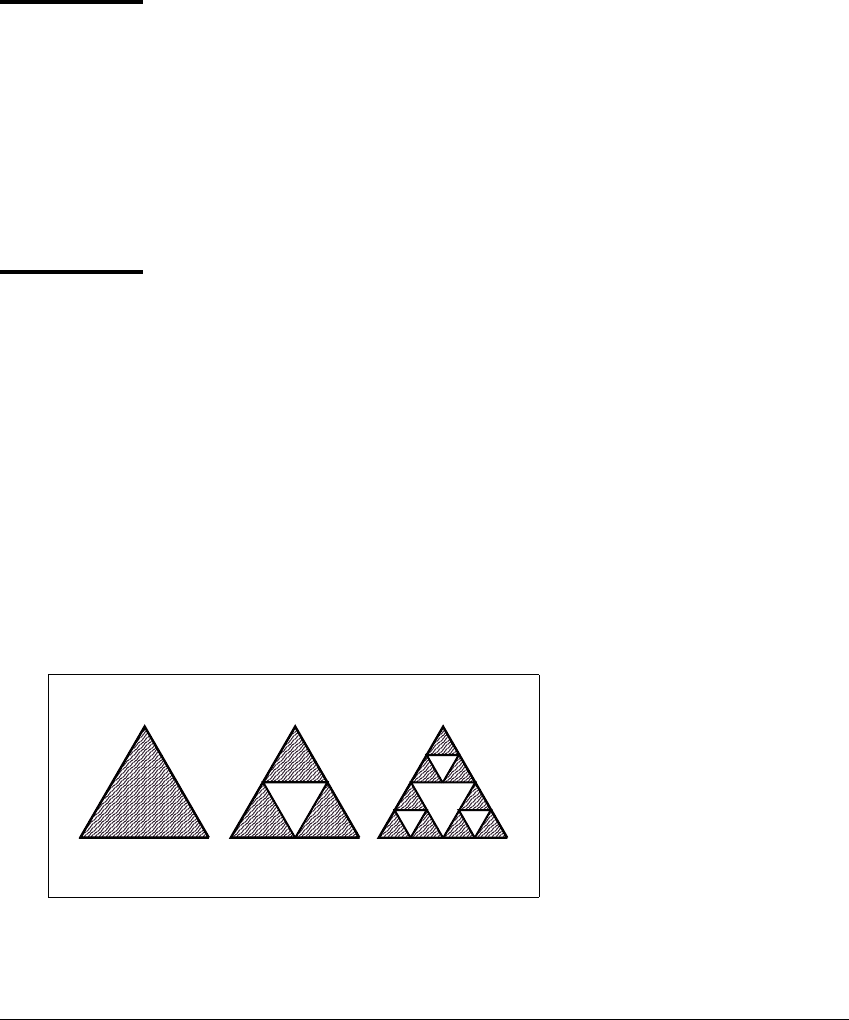
4.2 PROBABILISTIC C ONSTRUCTIONS OF F RACTALS

two-thirds of the way to the left and the top half two-thirds of the way to the

right in the skinny baker map is analogous to the thought experiment described

there.

E XAMPLE 4.6

The Cantor set construction of Example 4.1 can be altered to create inter-

esting fractals in the plane. Start with a triangle T

with vertices A, B, and C,as

in Figure 4.4. Delete the middle triangle from T

, where by middle triangle we

mean the one whose vertices are the midpoints of the sides of T

. The new shape

is the union of 3 subtriangles. Repeat the process indeﬁnitely by deleting the

middle triangles of the remaining 3 subtriangles of T

, and so on. The points that

remain make up the Sierpinski gasket.

E XAMPLE 4.7

As with the Cantor set, there is a probabilistic game that leads to the Sier-

pinski gasket. This game was introduced in Computer Experiment 4.1, although

the triangle differs from Figure 4.4. Let A, B, and C be the vertices of a triangle.

Start with a random point in the plane, and move the point one-half of the

distance to one of the vertices. Choose to move with equal likelihood toward

each of A, B, and C. From the new point, randomly choose one of the vertices

and repeat.

The attractor for this process is the Sierpinski gasket. Initial points asymp-

totically approach the attractor at an exponential rate. Except for the ﬁrst few

points, the picture is largely independent of the initial point chosen (as it is for

the Cantor set game). This is another example of an iterated function system.

B B C

Figure 4.4 Construction of the Sierpinski gasket.

Start with a triangle, remove the central triangle, and repeat with each remaining

triangle.

159

F RACTALS

✎ E XERCISE T4.3

(a) Find the maps f

, f

to express Example 4.6 as an iterated function

system. Assume that the triangle is equilateral with side-length one. (b) Find

the exponential convergence rate of an orbit to the attractor. That is, if

is a point inside the triangle with vertices A, B, and C, ﬁnd an upper

limit for the distance from the point x

of the orbit of the iterated function

system to the Sierpinski gasket.

E XAMPLE 4.8

A similar construction begins with a unit square. Delete a symmetric cross

from the middle, leaving 4 corner squares with side-length 1 3, as in Figure 4.5.

Repeat this step with each remaining square, and iterate. The limiting set of this

process is called the Sierpinski carpet.

✎ E XERCISE T4.4

Repeat Exercise T4.3 using the Sierpinski carpet instead of the gasket. Find

four maps and the exponential convergence rate.

➮ COMPUTER EXPERIMENT 4.2

Plot the Sierpinski gasket and carpet in the plane using the iterated function

systems developed in Exercises 4.3 and 4.4.

Figure 4.5 Construction of the Sierpinski carpet.

Remove a central cross from the square, and repeat for each remaining square.

160

4.3 FRACTALS FROM D ETERMINISTIC S YSTEMS

4.3 FRACTALS FROM DETERMINISTIC SYSTEMS

In this section we see how the complexities of the previous abstract examples

occur in familiar maps. One of the most basic maps on the real line is the tent

map, which we studied in Chapter 3. We deﬁne a slightly more general version

here. For a ⬎ 0, the tent map with slope a is given by

(x) ⫽



ax if x ⱕ 1 2

a(1 ⫺ x)if1 2 ⱕ x

This map is continuous, but not smooth because of the corner at x ⫽ 1 2.

In the case of the slope-2 tent map (a ⫽ 2), the unit interval I ⫽ [0, 1] is

mapped onto itself by T

(x). The itineraries and transition graph were developed

in Chapter 3, and it was noted that T

exhibits sensitive dependence on initial

conditions.

In the case 0 ⬍ a ⬍ 1, the tent map has a single ﬁxed point at 0, which is

attracting. All initial conditions are attracted to 0. For a ⬎ 1, the complement

of I maps to the complement of I. Therefore if a point x is mapped outside of

I, further iterations will not return it to I. For 1 ⱕ a ⱕ 2, the points of I stay

within I. For a ⬎ 2 most of the points of the unit interval eventually leave the

interval on iteration, never to return.

✎ E XERCISE T4.5

For the tent map, deﬁne the set L of all points x in [0, 1] such that f

(x) ⬍ 0

for some n.(a)Provethatiff

(x) ⬍ 0, then f

(x) ⬍ 0 for all k ⱖ n.(b)Prove

that for any a ⬎ 2, the length of L is 1 (the complement of L has measure

zero). (c) Prove that for 0 ⱕ a ⱕ 2, L ⫽⭋, the empty set.

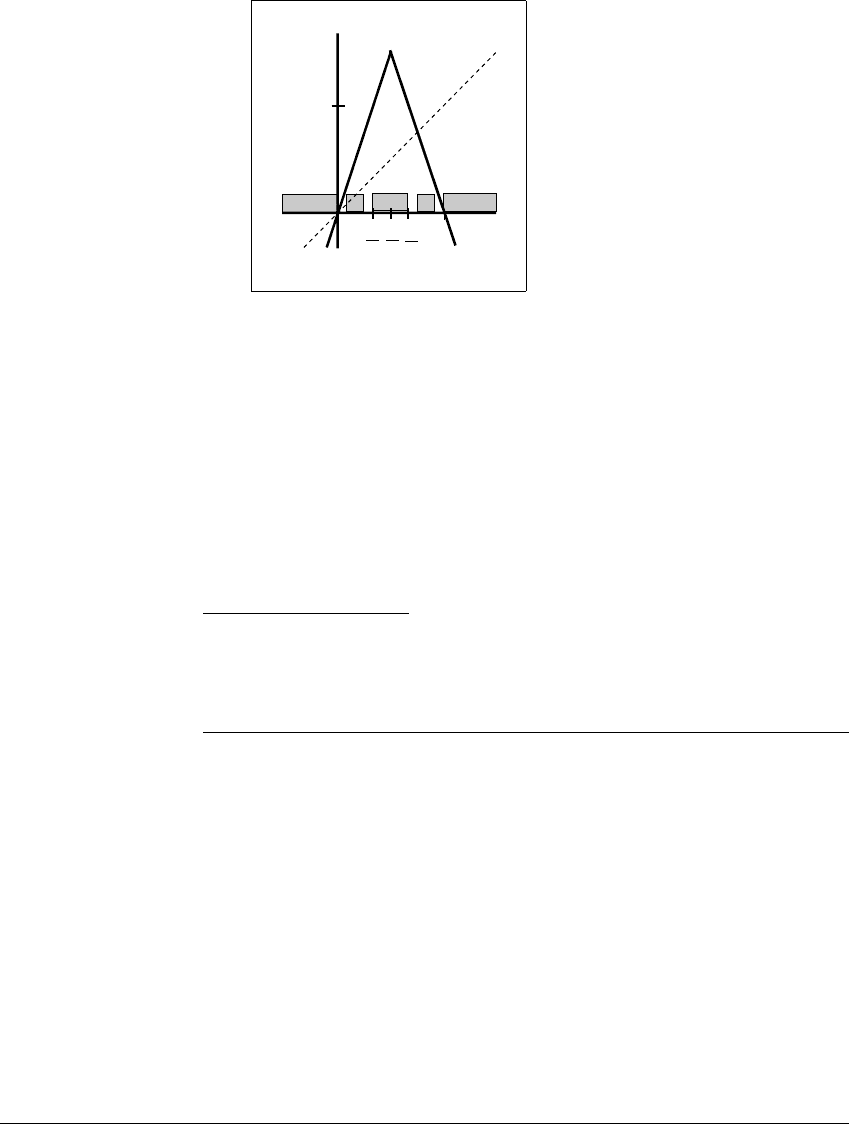
E XAMPLE 4.9

Consider the particular tent map T

, which is sketched in Figure 4.6. The

slope-3 tent map has dynamical properties that differ from those of the slope-2

tent map and its conjugate, the logistic map. For the slope-3 tent map, the basin

of inﬁnity is interesting. From the graph of T

in Figure 4.6, it is clear that initial

conditions in the intervals (⫺

⬁

, 0) and (1,

⬁

) converge to ⫺

⬁

upon iteration by

. The same is true for initial conditions in (1 3, 2 3), since that interval maps

into (1,

⬁

161

F RACTALS

Figure 4.6 The tent map with slope 3.

The shaded points map out of the unit interval after two or fewer iterations. There

is another region of points (not shown) that maps out after three iterations, and so

on. All points not lying in the middle-third Cantor set are attracted to ⫺

⬁

Let B be the basin of inﬁnity, the set of points whose orbits diverge

to ⫺

⬁

. So far we have noted that B contains (⫺

⬁

, 0) 傼 (1,

⬁

)aswellas

(1 3, 2 3), since T

(1 3, 2 3) 傺 (1,

⬁

). Further, B contains (1 9, 2 9), since

(1 9, 2 9) 傺 (1,

⬁

). The same goes for (7 9, 8 9). The pattern that is emerg-

ing here is summarized in the next exercise.

✎ E XERCISE T4.6

Show that B, the basin of inﬁnity of T

is the complement in ⺢

of the

middle-third Cantor set C.

The long-term behavior of points of ⺢

under T

can now be completely

understood. The points of B tend to ⫺

⬁

. The points of C, the remainder, bounce

around within C in a way that can be described efﬁciently using the base-3

representation of C.

Up to this point, the examples of this chapter are almost pathologically

well-organized. They are either the result of highly patterned constructions or, in

the case of iterated function systems, achieved by repeated applications of afﬁne

contraction mappings. Sets such as these that repeat patterns on smaller scales

are called self-similar. For example, if we magnify by a factor of three the portion

of the middle-third Cantor set that is in the subinterval [0, 1 3], we recover the

entire Cantor set. Next we will see that this type of regularity can develop in

more general nonlinear systems.

162

4.3 FRACTALS FROM D ETERMINISTIC S YSTEMS

(a) (b)

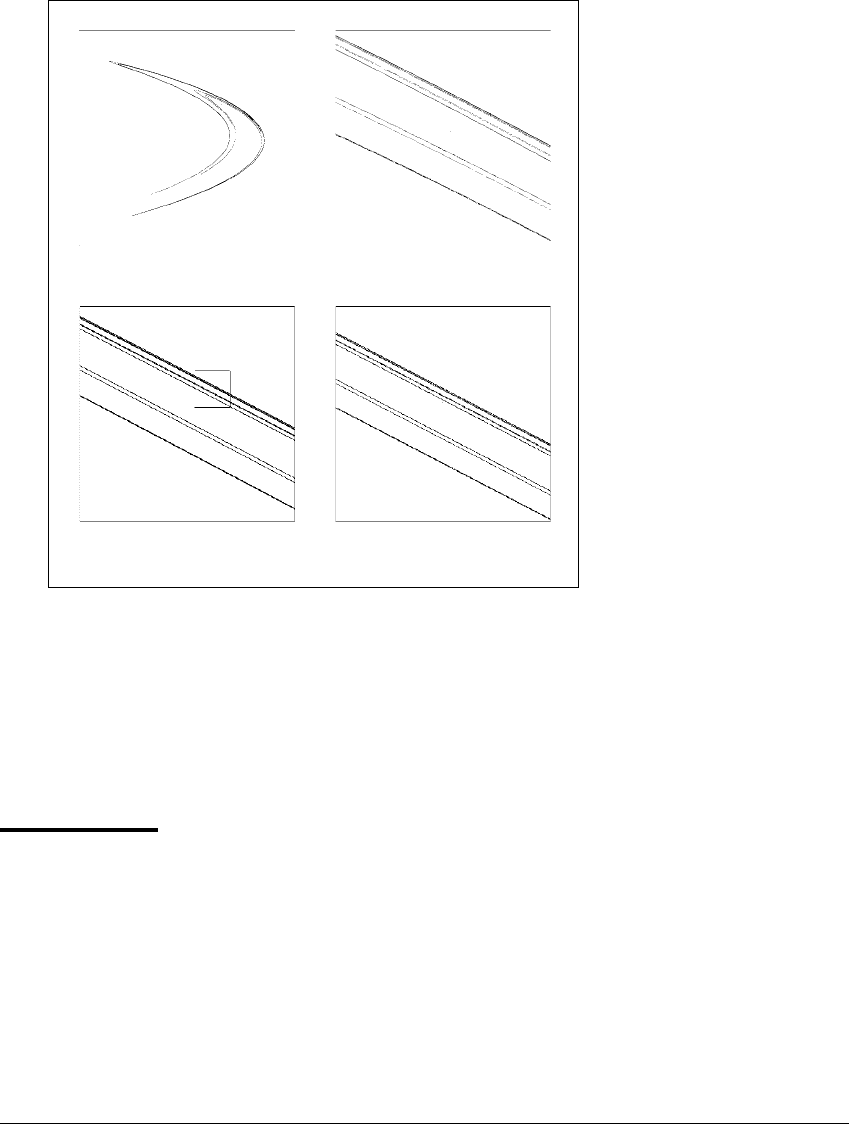
Figure 4.7 Self-similarity of the H

enon attractor.

(a) An attracting orbit of (4.1). Parts (b),(c),(d) are successive magni-

ﬁcations, showing the striated structure repeated on smaller and smaller

scales. This sequence is zooming in on a ﬁxed point. (a) [⫺2.5, 2.5] ⫻

[⫺2.5, 2.5]. (b) [0.78, 0.94] ⫻ [0.78, 0.94]. (c) [0.865, 0. 895] ⫻ [0.865, 0.895]. (d)

[0.881, 0.886] ⫻ [0.881, 0.886].

E XAMPLE 4.10

Figure 4.7(a) depicts an orbit of the H

enon map of the plane

f(x, y) ⫽ (1.4 ⫺ x

⫹ 0.3y, x). (4.1)

After ten million iterations, the orbit remains in the region shown but (appar-

ently) does not converge to a periodic orbit. M. H

enon proposed this map as an

example of a dynamical system with a fractal attractor. The orbit of almost any

initial point in this region will converge to this attractor. In Figure 4.7(b)(c)(d),

the attractor is shown on progressively smaller scales.

163

F RACTALS

E XAMPLE 4.11

Often, fractal structure is revealed indirectly, as in the case of basin bound-

aries. Consider, for example, the plane H

enon map with different parameter

values:

f(x, y) ⫽ (1.39 ⫺ x

⫺ 0.3y, x). (4.2)

Figure 4.8(a) shows in black all initial conditions in a rectangular region whose

orbits diverge to inﬁnity, that is, the basin of inﬁnity. The orbits of the initial

conditions colored white stay within a bounded region. In Figure 4.8(b)(c) suc-

cessive blow-ups reveal the fractal nature of the boundary between the black and

white regions.

4.4 FRACTAL BASIN BOUNDARIES

Figure 2.3 of Chapter 2 shows basins of a period-two sink of the H

enon map. In

part (a) of the ﬁgure, the basin boundary is a smooth curve. Part (b) of the ﬁgure

shows a much more complicated basin. In fact, the boundary between two basins

for a map of the plane can be far more complicated than a simple curve. In order

to understand how complicated boundaries can develop, we investigate a simple

model.

Consider a square R whose image is an S-shaped conﬁguration, mapping

across itself in three strips, as in Figure 4.9(a). The map also has two attracting

ﬁxed points outside the square, and we might assume that all points in the square

that are mapped outside the square to the left eventually go to the sink A

the left. Similarly, assume all points in this square that are mapped to the right

of the square will eventually go to the sink A

on the right. We will see that this

innocuous set of assumptions already implies a fractal basin boundary.

In Figure 4.9(b) the vertical strips shaded light grey represent points that

map out of the square to the left in one iterate, while points in the strips shaded

dark grey map out to the right in one iterate. The points in the three strips that are

not shaded stay in the square for one iterate. Each of these strips maps horizontally

across the square and contains two substrips which, on the next iteration, will map

to the left and two that map to the right. We could therefore think of continuing

the shading in this ﬁgure so that each white strip contains two light grey vertical

substrips alternating with two dark grey vertical substrips. The white substrips in

between will be further subdivided and points will be shaded or not, depending

164