Alligood K., Sauer T., Yorke J.A. Chaos: An Introduction to Dynamical Systems

Подождите немного. Документ загружается.

C HAOS IN T WO-DIMENSIONAL M APS

Deﬁnition 5.2 Let f be a map of ⺢

,mⱖ 1, and let 兵v

, v

,...其 be

a bounded orbit of f. The orbit is chaotic if

1. it is not asymptotically periodic,

2. no Lyapunov number is exactly one, and

3. L

) ⬎ 1.

In terms of Lyapunov exponents, part 3 of Deﬁnition 5.2 is equivalent to

) ⬎ 0.

E XAMPLE 5.3

The skinny baker map was deﬁned in Chapter 4. It is a map of the unit

square S in the plane which exhibits many typical properties of chaotic maps.

See Figure 4.3 of Chapter 4 to recall the geometric behavior. The equations are

written there, but we write them again in a slightly different form:

B(x

) ⫽

















if 0 ⱕ x

ⱕ







⫹



⫺1



⬍ x

ⱕ 1.

(5.1)

The middle third of the rectangles that remain are mapped out on each

iteration. Deﬁne the invariant set A of B to be the points that lie in B

(S) for

every positive and negative integer n. The invariant set is a middle-third Cantor

set of vertical lines. We call the set A invariant because it has the property that

⫺1

(A) ⫽ A.

✎ E XERCISE T5.1

Find the area of B

(S). Note that B is an area-contracting map, hence its

name.

We are interested in the following questions about the skinny baker map.

First, what are the Lyapunov exponents for orbits? Second, are there periodic

orbits, and what do they look like? Finally, are there chaotic orbits? We begin

with the ﬁrst question, which is relatively easy to answer. We will defer the

discussion of the periodic orbits until later in the chapter, where it will motivate

the development of a ﬁxed-point theorem and covering partitions in a direct

analogy with those concepts in Chapter 3.

196

5.1 LYAP U NOV E XPONENTS

The Jacobian matrix is constant for each point in the unit square for which

it is deﬁned:

DB(v) ⫽





for all v except along the discontinuity line x

⫽ 1 2. Consider a small circle of

radius r centered at a point in the unit square. After one iteration of the skinny

baker map, it is transformed into an ellipse with axes of length

r in the horizontal

direction and 2r in the vertical. After n iterates, the ellipse is (

)

r by 2

r.(Allof

this is true provided that the ellipses never map across the line x

⫽

,inwhich

case they get chopped in two on the next iterate. To avoid this, consider an even

smaller initial circle.) We conclude that the Lyapunov numbers of B are

and

2, or equivalently, that the Lyapunov exponents are ⫺ ln 3 and ln 2 for every

orbit. Since ln 2 ⬎ 0, every orbit that is not asymptotically periodic is chaotic.

Determining orbits that are not asymptotically periodic will be left for later in

the chapter.

✎ E XERCISE T5.2

Find a general formula for (area-contracting) skinny baker maps, where the

strips have width w instead of 1 3. Find the area contraction factor (per

iteration) and the Lyapunov exponents.

E XAMPLE 5.4

The cat map, introduced in Challenge 2 (Chapter 2), is also fairly simple

to analyze for Lyapunov exponents. The map on the unit square in ⺢

is deﬁned





⫽







(mod 1) ⫽ Av (mod 1).

The Jacobian matrix Df(v) is the constant matrix A for any point v. Unlike the

skinny baker map case, it is not diagonal, so we turn to Theorem 2.24 of Chapter

2 in order to calculate the ellipses formed by applying f to an inﬁnitesimal disk.

The theorem says that the axes of the ellipse formed by applying f

will be

the square roots of the eigenvalues of A

)

.SinceA is a symmetric matrix

(A ⫽ A

), these are the same as the eigenvalues of A

, which can be found as e

where e

are the eigenvalues of A. We calculate e

⫽ (3 ⫹



5) 2 ⬇ 2.618 and

⫽ (3 ⫺



5) 2 ⬇ 0.382. The product of the two eigenvalues is 1 ⫽ det(A).

197

C HAOS IN T WO-DIMENSIONAL M APS

This tells us that a disk of radius r is transformed into an ellipse with axes re

and re

by the cat map, and into an ellipse with axes re

and re

by n applications

of the cat map. Since e

⬎ 1ande

⬍ 1, the ﬁxed point 0 ⫽ (0, 0) is a saddle.

The Lyapunov numbers L

and L

for the ﬁxed point 0 and for any other orbit of

the cat map are e

and e

, and the Lyapunov exponents are h

⫽ ln e

⬇ 0.962

and h

⫽ ln e

⬇ ⫺0.962.

The cat map is unusual in that the Jacobian matrix Df is independent of

v. Ordinarily, unless the orbit is periodic, computing eigenvalues of individual

Jacobians tells nothing about Lyapunov numbers.

Since every orbit of the cat map has a positive Lyapunov exponent (and

no Lyapunov exponent equal to 0), any orbit that is not asymptotically periodic

will be chaotic. In the remainder of this example, we argue that a large number

of orbits are not asymptotically periodic.

By Step 4 of Challenge 2, the periodic points of the cat map are those points

in the unit square with both coordinates rational. This set is countable. Since all

periodic orbits are saddles, the only asymptotically periodic orbits are these saddles

and the orbits of points on their stable manifolds. As described in Chapter 2, the

stable manifold of a saddle in the plane is a one-dimensional curve containing

the saddle point. In the case of the cat map, a stable manifold emanates from a

saddle at an irrational angle (from the horizontal). In order to understand the

behavior of a stable manifold globally, we need to think of the cat map as deﬁned

on the torus (as described in Challenge 2), where it is continuous. Any one stable

manifold will then wind around the torus without end. Viewing the torus as the

unit square with left and right sides glued and top and bottom glued, we can see

how this curve repeatedly crosses the line segment I ⫽ 兵(x, 0) : 0 ⱕ x ⬍ 1其, a

cross-sectional circle on the torus.

Following one branch of the stable manifold as it emanates from a saddle p,

we count successive crossings of the manifold with I. Since the slope is irrational,

there will be inﬁnitely many of these crossings; however, the set of all crossings

will be countable. (This can be seen by the fact that there is a deﬁnite ordering

of the crossings as we follow the stable manifold from p.) Taking the union of all

crossings for all stable manifolds, we have a countable union of countable sets,

which is again countable. Since I contains an uncountable number of points,

there must be points in I that are not on any stable manifold. Therefore, the cat

map has chaotic orbits.

In Deﬁnition 5.2 the condition that 0 not be a Lyapunov exponent (of a

chaotic orbit) is included to rule out cases of “quasiperiodicity”, as illustrated by

the next example.

198

5.2 NUMERICAL C ALCULATION OF LYA PU N OV E XPONENTS

E XAMPLE 5.5

Let

f(r,

␪

) ⫽ (r

␪

⫹ q),

where r and

␪

are polar coordinates, and q is an angle irrationally related to 2

␲

The orbits of all points inside the unit circle converge to the origin, which is a

ﬁxed point. The unit circle is invariant under f, as points on it rotate through the

angle q. Outside the unit circle, orbits are unbounded. The quasiperiodic orbits at

r ⫽ 1 have Lyapunov exponents ln 2 and 0. Although they are not asymptotically

periodic and they do exhibit sensitive dependence (due to a positive Lyapunov

exponent in the r direction), we do not want the deﬁnition of “chaotic orbit” to

apply to these orbits since their motion is quite predictable.

➮ COMPUTER EXPERIMENT 5.1

Plot the orbit of the two-dimensional Tinkerbell map

f(x, y) ⫽ (x

⫺ y

⫹ c

x ⫹ c

y, 2xy ⫹ c

x ⫹ c

where c

⫽⫺0.3, c

⫽⫺0.6, c

⫽ 2, c

⫽ 0.5, with initial value (x, y) ⫽

(0.1, 0.1). The orbit tends toward an oval-shaped quasiperiodic attractor. Find

out what replaces the quasiperiodic attractor when the parameter c

is decreased

or increased.

5.2 NUMERICAL CALCULATION OF

LYAPUNOV EXPONENTS

For most interesting maps, there is no direct way to determine Lyapunov expo-

nents from knowledge of the map and its Jacobian matrices. The skinny baker

map and the cat map of the previous section are exceptions to this rule. Nor-

mally, the matrix J

⫽ Df

) is difﬁcult to determine exactly for large n,and

we must resort to the approximation of the image ellipsoid J

N of the unit sphere

by computational algorithms.

199

C HAOS IN T WO-DIMENSIONAL M APS

The ellipsoid J

N has semi-major axes of length s

in the directions u

.The

direct approach to calculating the Lyapunov exponents would be to explicitly form

and ﬁnd its eigenvalues s

. In the case that the ellipsoid has stretching and

shrinking directions, it will be very long and very thin for large n. The eigenvalues

of J

will include both very large and very small numbers. Because of the

limited number of digits allowed for each stored number, computer calculations

become difﬁcult when numbers of vastly different sizes are involved in the same

calculation. The problem of computing the s

gets worse as n increases. For this

reason, the direct calculation of the ellipsoid J

N is usually avoided.

The indirect approach that works better in numerical calculations involves

following the ellipsoid as it grows. Since

U ⫽ Df(v

n⫺1

) ⭈⭈⭈Df(v

)N, (5.2)

we can compute one iterate at a time. Start with an orthonormal basis

兵w

,...,w

其 for ⺢

, and compute the vectors z

,...,z

⫽ Df(v

,...,z

⫽ Df(v

. (5.3)

These vectors lie on the new ellipse Df(v

)N, but they are not necessarily orthog-

onal. We will remedy this situation by creating a new set of orthogonal vectors

兵w

,...,w

其 which generate an ellipsoid with the same volume as Df(v

)N.

Use the Gram-Schmidt orthogonalization procedure, which deﬁnes

⫽ z

⫺

⭈ y

||y

⫽ z

⫺

⭈ y

||y

⫺

⭈ y

||y

⫽ z

⫺

⭈ y

||y

⫺⭈⭈⭈⫺

⭈ y

m⫺1

||y

m⫺1

, (5.4)

where ⭈ denotes the dot or scalar product and || ⭈ || denotes Euclidean length.

Notice what the equations do: First z

is declared to be kept as is in the new

set. The part of z

which is perpendicular to z

is retained as y

; the term being

subtracted away is just the projection of z

to the z

direction. The vector y

deﬁned to be the part of z

perpendicular to the plane spanned by z

and z

,and

so on.

200

5.2 NUMERICAL C ALCULATION OF LYA PU N OV E XPONENTS

✎ E XERCISE T5.3

Write the result of the Gram-Schmidt orthogonalization procedure as an

m ⫻ m matrix equation Z ⫽ YR, where the columns of Y are y

,...,y

the columns of Z are z

,...,z

,andR is an upper triangular matrix. Show

that det(R) ⫽ 1, so that det(Y) ⫽ det(Z). Explain why this implies that the

ellipsoids YN and ZN have equal m-dimensional volume. Depending on your

matrix algebra skills, you may want to start with the case m ⫽ 2.

According to Exercise T5.3, if we set w

⫽ y

,...,w

⫽ y

for the new

orthogonal basis, they will span an ellipsoid of the same volume as Df(v

)N.

Next apply the Jacobian Df(v

) at the next orbit point, and reorthogonalize

the set

Df(v

,...,Df(v

(5.5)

to produce a new orthogonal set 兵w

,...,w

其. Repeating this step n times gives

aﬁnalset兵w

,...,w

其 of vectors which approximate the semi-major axes of the

ellipsoid J

The total expansion r

in the ith direction after n iterations, referred to in

Deﬁnition 5.1, is approximated by the length of the vector w

.Thus||w

1 n

the approximation to the ith largest Lyapunov number after n steps.

To eliminate the problem of extremely large and small numbers, this algo-

rithm should be amended to normalize the orthogonal basis at each step. Denote

the y vectors recovered from the application of Gram-Schmidt orthogonalization

Df(v

,...,Df(v

by y

j⫹1

,...,y

j⫹1

.Setw

j⫹1

⫽ y

j⫹1

 ||y

j⫹1

||, making the w

j⫹1

unit vectors. Then

||y

j⫹1

|| measures the one-step growth in direction i, and since r

⬇ ||y

|| ⭈⭈⭈||y

||,

the expression

ln ||y

|| ⫹⭈⭈⭈⫹ln ||y

is a convenient estimate for the ith largest Lyapunov exponent after n steps.

E XAMPLE 5.6

Consider the H

enon map introduced in Chapter 2 with parameters a ⫽ 1.4

and b ⫽ 0.3. Typical initial conditions have Lyapunov exponents which can be

approximated by the method described above. Reasonably accurate approxima-

tions are h

⫽ 0.42 and h

⫽⫺1.62.

201

C HAOS IN T WO-DIMENSIONAL M APS

Figure 5.3 The Ikeda attractor of Example 5.7.

The attractor has fractal structure and a largest Lyapunov exponent of approximately

0.51.

E XAMPLE 5.7

The Ikeda map is given by

F(x, y) ⫽ (R ⫹ C

(x cos

␶

⫺ y sin

␶

),C

(x sin

␶

⫹ y cos

␶

)), (5.6)

where

␶

⫽ C

⫺ C

 (1 ⫹ x

⫹ y

), and R, C

, and C

are real parameters.

This map was proposed as a model, under some simplifying assumptions, of the

type of cell that might be used in an optical computer. The map is invertible with

Jacobian determinant C

for each (x, y), therefore L

⫽ C

. In certain ranges

of the parameters, there are two ﬁxed point sinks, corresponding to two stable

light frequencies in the cell. Setting R ⫽ 1,C

⫽ 0.4,C

⫽ 0.9, and C

⫽ 6,

one of these sinks has developed into what is numerically observed to be a

chaotic attractor, with Lyapunov numbers L

⫽ 1.66 and L

⫽ 0.487 (Lyapunov

exponents 0.51 and ⫺0.72). The orbit of one initial condition is shown in Figure

5.3. The orbits of most initial points chosen in a neighborhood of the attractor

appear to converge to the same limit set.

➮ COMPUTER EXPERIMENT 5.2

Write a program to measure Lyapunov exponents. Check the program by

comparing your approximation for the H

enon or Ikeda map with what is given in

202

5.3 LYAP U NOV D IMENSION

the text. Calculate the Lyapunov exponents of the Tinkerbell map quasiperiodic

orbit from Computer Exercise 5.1 (one should be zero). Finally, change the ﬁrst

parameter of Tinkerbell to c

⫽ 0.9 and repeat. Plot the orbit to see the graceful-

looking chaotic attractor which gives the map its name.

5.3 LYAPUNOV DIMENSION

There is a relationship between the Lyapunov exponents and the fractal dimen-

sion of a typical chaotic attractor. A deﬁnition of dimension that acknowledges

this relationship has been proposed, called the Lyapunov dimension. In general,

this dimension gives a different number than the box-counting dimension, al-

though they are usually not far apart. The appealing feature of this dimension is

that it is easy to calculate, if the Lyapunov exponents are known. No boxes need

to be counted. We will begin with the deﬁnition, which is fairly simple to state,

and then explain where it comes from.

Deﬁnition 5.8 Let f be a map on ⺢

. Consider an orbit with Lyapunov

exponents h

ⱖ ⭈⭈⭈ ⱖ h

,andletp denote the largest integer such that



i⫽1

ⱖ 0. (5.7)

Deﬁne the Lyapunov dimension D

of the orbit by

⫽











0ifnosuchp exists

p ⫹

p⫹1



i⫽1

if p ⬍ m

m if p ⫽ m

(5.8)

In the case of a two-dimensional map with h

⬎ 0 ⬎ h

and h

⫹ h

⬍ 0

(for example, the H

enon map and the skinny baker map), (5.8) yields

⫽ 1 ⫹

. (5.9)

Inserting the Lyapunov exponents for the skinny baker map into the Lyapunov

dimension formula yields

⫽ 1 ⫹

ln 2

ln 3

. (5.10)

203

C HAOS IN T WO-DIMENSIONAL M APS

This number exactly agrees with the box-counting dimension of the skinny baker

invariant set (see Exercise T4.9). To be precise, the deﬁnition of Lyapunov di-

mension applies to an orbit. In dealing with an arbitrary invariant set, such as a

chaotic attractor, we are making the assumption that the orbit whose dimension

we have calculated is in some way representative of the invariant set. For exam-

ple, we have seen that the invariant set of the logistic map (the unit interval)

contains a dense orbit. (Recall that a “dense” orbit is one that comes arbitrarily

close to each point in the invariant set.) The idea of chaotic attractors contain-

ing representative orbits (and, in particular, dense orbits) is developed further in

Chapter 6.

All that remains is to explain the reasoning behind the deﬁnition. We start

with an invariant set of a map on ⺢

, such as that of the skinny baker map. We

assume that the Lyapunov exponents satisfy h

ⱖ 0 ⱖ h

and h

⫹ h

⬍ 0. There

is one direction with a stretching factor of e

⬎ 1 per iterate (on average), and a

perpendicular direction with shrinking factor 0 ⬍ e

⬍ 1. In the vicinity of the

orbit, areas change at a rate proportional to e

⫽ e

⫹h

⬍ 1 per iterate, which

means that they decrease toward zero.

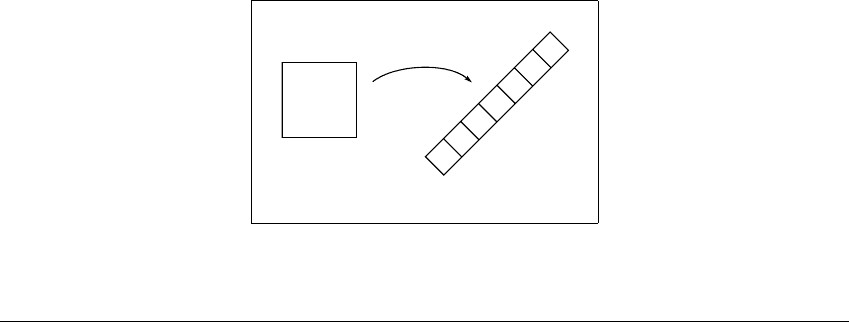
Figure 5.4 illustrates the situation. A small square of side d becomes (approx-

imately) a rectangle with sides de

and de

after k iterates of the map f. The area

is d

⫹h

)

, which tends to zero, but the dimension of the resulting invariant set

is at least 1, due to the expansion in one direction. Assuming that the invariant

set of the map is bounded, the box shrinks down into a long one-dimensional

curve that eventually doubles back on itself; this is repeated indeﬁnitely. We

expect the dimension of the invariant set to be one plus a fractional amount due

to fractal structure perpendicular to the expanding direction.

With this picture in mind, we can count boxes as we did in Chapter 4, the

difference being that instead of having an actual set to cover, all we have is Figure

5.4. We can cover the image of the initial box under f

by de

 de

boxes of

Figure 5.4 Image of a square under a plane map.

A square of side d is mapped approximately into a rectangle by f

204

5.3 LYAP U NOV D IMENSION

side

⑀

⫽ de

. Proceeding as in the case of box dimension, we ﬁnd that for an

invariant set which can be covered by N(

⑀

) boxes of side length

⑀

ln N(

⑀

)

⫺ ln

⑀

⬇ ⫺

ln N(d)e

k(h

⫺h

)

ln de

⫽⫺

k(h

⫺ h

) ⫹ ln N(d)

⫹ ln d

(5.11)

⫽

⫺ h

⫹ [ln N(d)] k

⫺ (ln d) k

If we let the box size

⑀

go to zero by letting k approach inﬁnity, we ﬁnd the value

1 ⫺ h

 h

for the dimension. We call the result of this heuristic argument the

Lyapunov dimension D

⫽ 1 ⫹ h

 |h

|, which agrees with our general deﬁnition

above.

E XAMPLE 5.9

The Lyapunov dimension of the invariant set of the H

enon map discussed

above is 1 ⫹ 0.39 1.59 ⬇ 1.25.

✎ E XERCISE T5.4

Find the Lyapunov dimensions of the invariant sets of the cat and Ikeda

maps described above.

For completeness, note that the case 0 ⬎ h

ⱖ h

is trivial, since it corre-

sponds to an invariant set that is discrete (such as a periodic sink). The formula

(5.8) gives 0 in this case. If 0 ⬍ h

ⱕ h

, area is expanding on the bounded

invariant set, and the formula gives a dimension of 2.

To complete this section we will extend our heuristic argument to higher

dimensions, in order to understand the deﬁnition of Lyapunov dimension for maps

on ⺢

. To decide on the size of boxes that are relevant, we need to ﬁnd the largest

integer p for which p-dimensional volume is not shrinking under the application

of the map f. For example, for the area-contracting H

enon map of Example 5.6,

p ⫽ 1, since area is contracting by a factor of 0.3 per iteration, while the map

is typically expanding in one direction. Then we visualize the invariant set as

p-dimensional tubes winding around one another, giving a dimension somewhat

larger than p. It is clear that p is the largest integer such that e

⫹...⫹h

ⱖ 1, or

equivalently, such that h

⫹⭈⭈⭈⫹h

ⱖ 0.

We will illustrate a couple of interesting cases in ⺢

, assuming that there

is a single positive Lyapunov exponent. With the assumption h

⬎ 0 ⬎ h

ⱖ h

(5.8) distinguishes two cases, depending on the sign of h

⫹ h

. Thus arises the

spaghetti-lasagna dichotomy.

205