Alligood K., Sauer T., Yorke J.A. Chaos: An Introduction to Dynamical Systems

Подождите немного. Документ загружается.

C HAOS IN T WO-DIMENSIONAL M APS

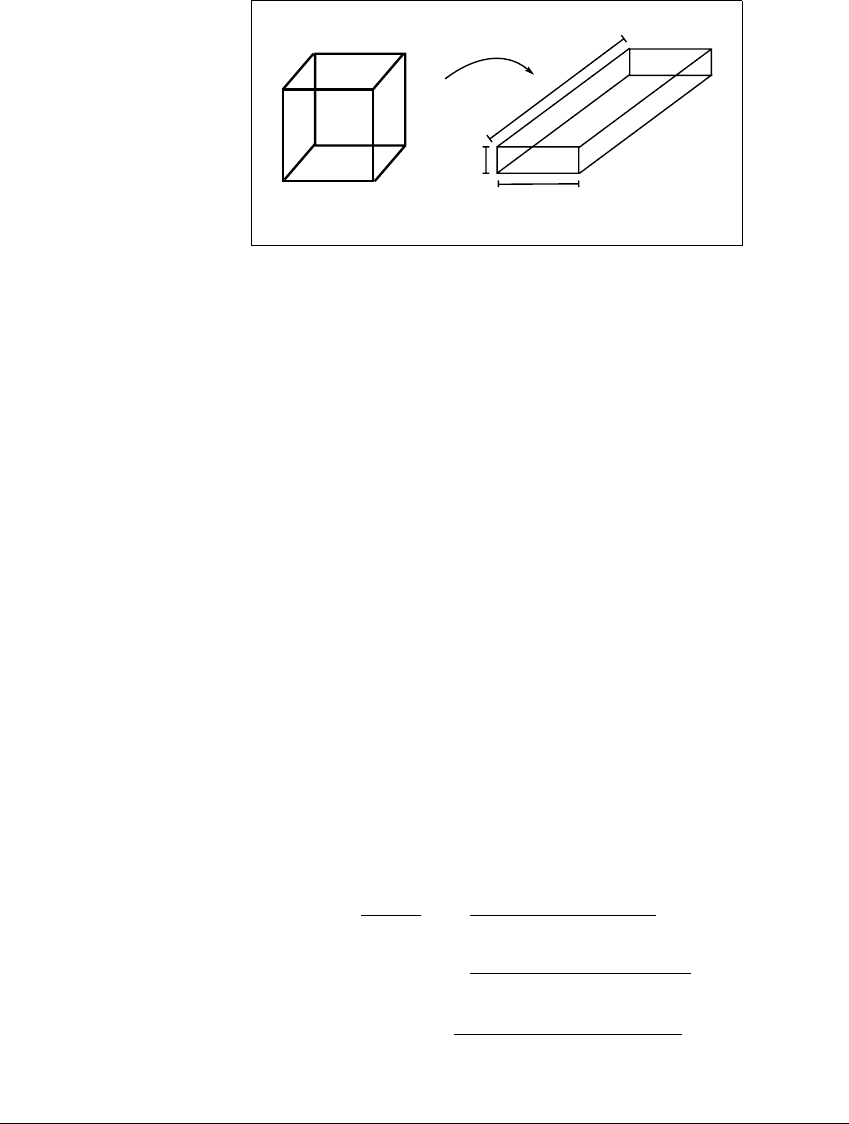
Figure 5.5 Three-dimensional version of Figure 5.4.

A small cube of side d maps into box.

Case 1. h

⫹ h

⬍ 0.

In this case p ⫽ 1, meaning that the box in Figure 5.5 shrinks toward a

one-dimensional curve which winds around itself as in Figure 5.6(a). The curves

have lengths and widths regulated by h

and h

, while the perpendicular direction

associated to h

is irrelevant, since the invariant set contracts to a plane (locally) in

this direction. Ignoring this direction, we cover the invariant set by 2-dimensional

boxes of side de

as in Figure 5.4, and get D

⫽ 1 ⫹ h

 |h

Case 2. h

⫹ h

ⱖ 0.

Now p ⫽ 2, so that the invariant set is the limiting case of two-dimensional

“ribbons” winding throughout a bounded region of ⺢

, as in Figure 5.6(b). The

fractal width of this limit will be decided by the h

direction. Imagine cutting up

the rectangles with thickness in this ﬁgure into three-dimensional cubes of side

. The number we need is the product of e

 e

along one direction and

 e

along the other. In total, it takes e

k(h

⫺h

)

⫻ e

k(h

⫺h

)

of these boxes to

cover, resulting in

ln N(

⑀

)

⫺ ln

⑀

⬇ ⫺

ln N(d)e

k(h

⫺h

)⫹k(h

⫺h

)

ln de

⫽⫺

k(h

⫹ h

⫺ 2h

) ⫹ ln N(d)

⫹ ln d

⫽

⫺ h

⫹ [ln N(d)] k

⫺ (ln d) k

, (5.12)

which approaches D

⫽ 2 ⫹ (h

⫹ h

) |h

| in the limit as k →

⬁

,sinceh

⬍ 0.

206

5.4 A TWO-DIMENSIONAL F IXED-POINT T HEOREM

(a) (b)

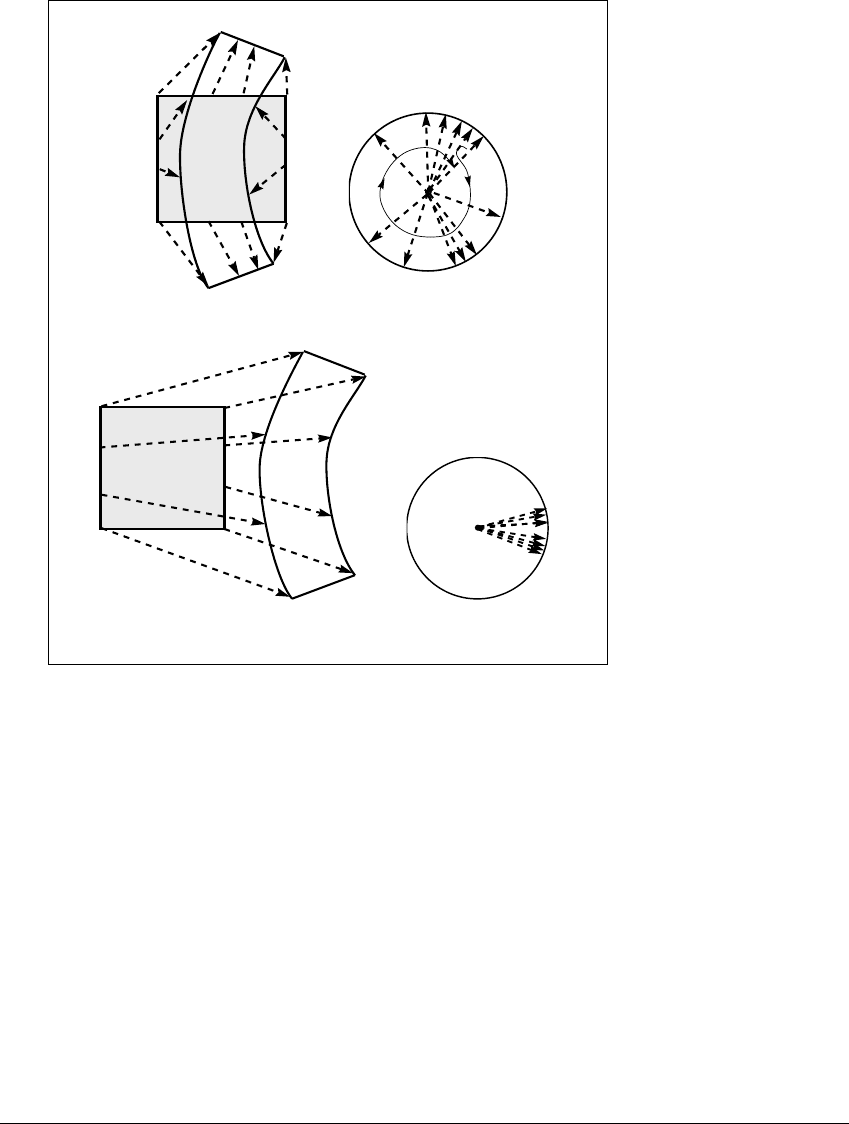
Figure 5.6 The spaghetti-lasagna dichotomy.

(a) Illustration of Case 1. Since h

⫹ h

⬍ 0, a cube eventually shrinks into strands

of spaghetti. (b) In Case 2, where h

⫹ h

ⱖ 0, you get lasagna.

The general case is an extension of this reasoning. Assuming that h

⫹⭈⭈⭈⫹

ⱖ 0andh

⫹⭈⭈⭈⫹h

⫹ h

p⫹1

⬍ 0, we can use (p ⫹ 1)-dimensional boxes of side

p⫹1

. The number of boxes needed is e

k(h

⫺h

p⫹1

)

⫻ e

k(h

⫺h

p⫹1

)

⫻⭈⭈⭈⫻e

k(h

⫺h

p⫹1

)

resulting in a Lyapunov dimension of

ln N(

⑀

)

⫺ ln

⑀

⬇ ⫺

k(h

⫹ ...⫹ h

⫺ ph

p⫹1

)

p⫹1

⫹ ln d

→ p ⫹

⫹ ...⫹ h

p⫹1

. (5.13)

5.4 A TWO-DIMENSIONAL

FIXED-POINT THEOREM

In Section 3.4 of Chapter 3, we developed a ﬁxed-point theorem in conjunc-

tion with itineraries for the purpose of determining the periodic points of one-

dimensional maps. A two-dimensional analogue is shown in Figure 5.7. Start with

a geographical map of a rectangular area, say the state of Colorado. Take a second

identical map, shrink it in one direction, stretch it in the other, and lay it across

the ﬁrst. Then there must be a point in Colorado that lies exactly over itself in

the two maps. The exact orientation of the maps is not important; if the top map

is moved a little from the position shown in Figure 5.7, the ﬁxed point may be

moved slightly, but there will still be one. The principal hypothesis is that the

horizontal sides of the top map are both outside the horizontal sides of the lower

207

C HAOS IN T WO-DIMENSIONAL M APS

COLORADO

Denver

COLORADO

Figure 5.7 The Colorado Corollary.

If a map of Colorado is overlaid with a stretched version of the same map, then

there must be a place in the state lying over itself on the two maps.

map, and the vertical sides of the top one are both inside the vertical sides of the

lower one.

We want to extract the fundamental elements of this interesting fact and

explain why it works. Let f be a continuous map on the plane and S be a rectangular

region. Imagine the image f(S) as some deformed version of a rectangle (as in

Figure 5.8). Now consider restricting your view of the map to the boundary of S

only. In the ﬁgure, vectors are drawn connecting each point v on the boundary

to its image point f(v). If you begin at one point on the rectangle boundary and

make one trip around, returning to where you started, the (directions of the)

vectors V(x) ⫽ f(x) ⫺ x will make an integer number of turns. The vectors will

travel through a cumulative n ⭈ 360

◦

for some integer n.Hereweareconsidering

the net effect of going around the entire boundary; the vectors could go several

turns in one direction, and then unwind to end up with zero net turns by the time

you return to the starting point. The net rotations must be an integer, since you

return to the vector V(x) where you started. In Figure 5.8, part (a) shows a net

rotation of 1 turn on the boundary, while part (c) shows a net rotation of 0 turns.

The next theorem guarantees that (a) implies the existence of a ﬁxed point; (c)

does not.

Theorem 5.10 Let f be a continuous map on ⺢

, and S a rectangular region

such that as the boundary of S is traversed, the net rotation of the vectors f(x) ⫺ x is

nonzero. Then f has a ﬁxed point in S.

Proof: There is nothing to do if the center c of the rectangle is already a

ﬁxed point. If it isn’t, we slowly shrink the rectangle down from its original size

to the point c, and ﬁnd a ﬁxed point along the way. As the rectangle shrinks,

208

5.4 A TWO-DIMENSIONAL F IXED-POINT T HEOREM

e f

(a) (b)

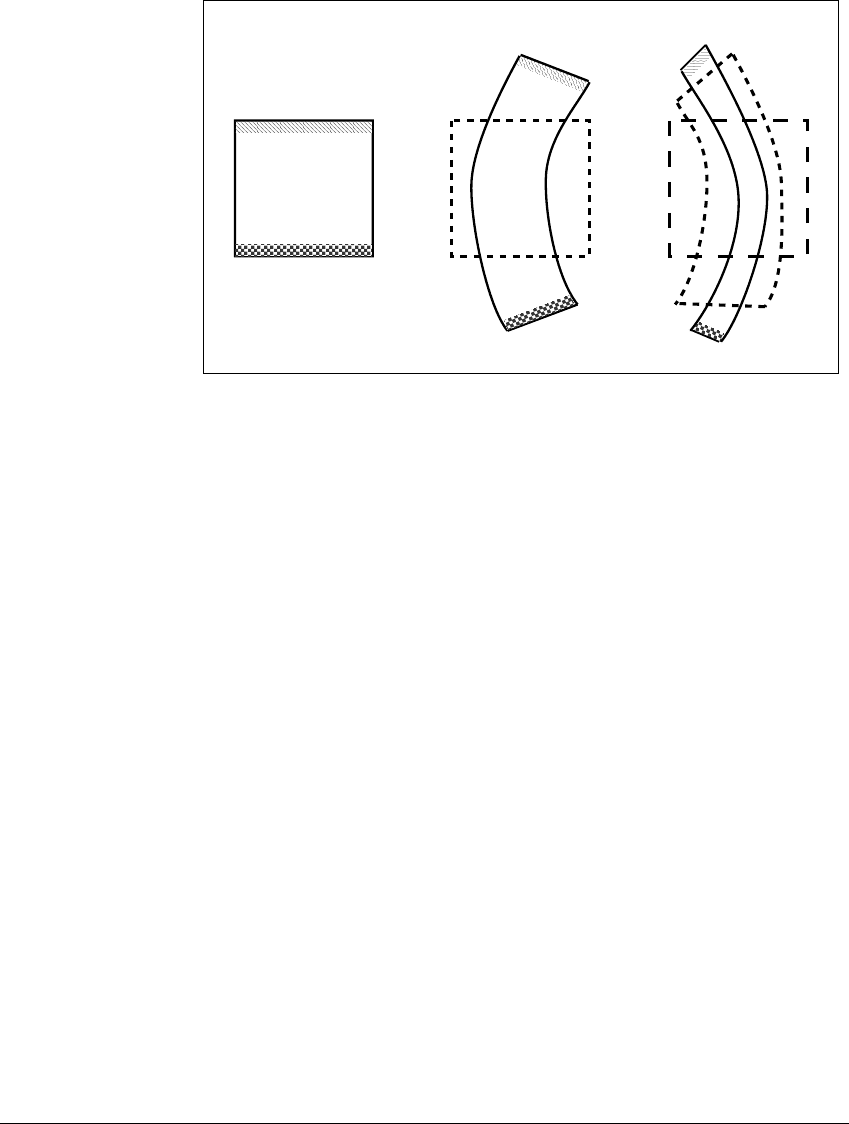
Figure 5.8 Illustration of Fixed-Point Theorem.

A direction V(x) ⫽ f(x) ⫺ x is deﬁned for each x on the rectangle’s boundary,

assuming that f(x) ⫺ x is never zero on the boundary. (a) As x is followed counter-

clockwise around the rectangle, the directions V(x) make one complete clockwise

turn when f(S) lies across S. (b) The direction vectors from (a) are normalized to

unit length and moved to a unit circle. A net rotation of one can be seen. (c) A

rectangle on which the map does not have a ﬁxed point. (d) The vector directions

have a net rotation of zero turns.

the image shrinks, and the vectors V(x) deﬁned along the boundary of S change

continuously, but they must continue to make at least one full turn, unless there

is some point x where the direction V(x) fails to make sense because V(x) ⫽



(The net rotation is an integer and cannot jump from one integer to another while

the vector directions are changing continuously.) Of course, V(x) ⫽



0 implies a

ﬁxed point x ⫽ f(x).

209

C HAOS IN T WO-DIMENSIONAL M APS

But this failure must occur, because when the shrinking rectangle gets small

enough, its image must move completely away from it, as in Figure 5.8(c), since

f(c) is a nonzero distance from c,andf is continuous. At this point the net rotation

of V(x) is zero, so that such a failure must have occurred sometime during the

shrinking process.

What is really happening here is that as we shrink the rectangle, we will in

fact develop a ﬁxed point on the boundary of the rectangle, so the net rotation

is not deﬁned. At this point the net rotation can jump discontinuously. As the

rectangle gets very small, all the vectors on its boundary nearly point in the same

direction and the net rotation must be zero.

In fact, this technique could be used to locate a ﬁxed point. Consider a

computer program that computes the net rotation for a rectangle; then when

the rectangle has a nonzero rotation number, the program shrinks the rectangle

slightly. The rotation number will be unchanged. The program keeps shrinking

it until the rotation number suddenly jumps. This locates a rectangle with a ﬁxed

point on it. The program could then search the rectangle’s boundary to locate the

ﬁxed point with high accuracy.

More about ﬁxed point theorems and the use of net rotation, or winding

number, to prove them can be found in texts on elementary topology (Chinn and

Steenrod, 1966).

Remark 5.11 The Fixed-Point Theorem is a property of the topology of

the map alone, and doesn’t depend on starting with a perfect rectangle, as long

as the region has no holes.

Figure 5.9(a) shows a general rectangular set S, and part (b) shows an image

f(S) lying across S, similar to the situation with the map of Colorado. Note that

f(S

) lies entirely to the right of S

, f(S

) lies entirely to the left of S

, f(S

) lies

entirely above S

,andf(S

) lies entirely below S

. These facts imply that the

net rotation is one counterclockwise turn. The theorem says that there must be a

ﬁxed point lying in S.

✎ E XERCISE T5.5

Prove the Brouwer Fixed-Point Theorem in two dimensions: If f is a one-

to-one map, S is a square and f(S) is contained in S, then there is a ﬁxed

point in S.

210

5.4 A TWO-DIMENSIONAL F IXED-POINT T HEOREM

f(S

)

f(S

)

f(S

)

f(S

)

f(S

)

f(S

)

f(S

)

f(S

)

(a) (b) (c)

Figure 5.9 The setting for Corollary 5.12.

(a) The domain rectangle S. (b) The image f(S) lies across S consistent with the

hypotheses of Corollary 5.12. There must be a ﬁxed point of f inside S.(c)Another

way the hypotheses can be satisﬁed.

We summarize these ideas in the next corollary. Check that the nonzero

rotation hypothesis of Theorem 5.10 is satisﬁed by the hypothesis of Corollary

5.12.

Corollary 5.12 (The Colorado Corollary.) Let f be a continuous map

on ⺢

,andletS be a rectangle in ⺢

with vertical sides s

and s

, and horizontal

sides s

and s

. Assume that f(s

)andf(s

) are surrounded by s

and s

(in

terms of x-coordinates) and that f(s

)andf(s

) surround s

and s

(in terms of

y-coordinates). Then f has a ﬁxed point in S.

Referring to Figure 5.10, we will say that “f(A) lies across B vertically” if

the images of the right and left sides of A lie inside the right and left sides of B (in

terms of x-coordinates), and the images of the top and bottom sides lie outside

B, one on or above the top of B and one on or below the bottom of B.Thereis

a similar deﬁnition where f(A) lies across B horizontally. In fact, if f is invertible

and f(A) lies across B,thenf

⫺1

(B) lies across A.

Note that this “lying across” property is transitive. That is, if f(A) lies

across B and if f(B) lies across C with the same orientation, then some curvilinear

subrectangle of f

(A) lies across C with this orientation. (See Figure 5.10.) If

211

C HAOS IN T WO-DIMENSIONAL M APS

f(B)

(A)

f(A)

Figure 5.10 Transitivity of “lying across”.

If f(A) lies across B,andf(B) lies across C,thenf

(A) lies across C.

there is a sequence S

...S

such that f(S

) lies across S

, f(S

) lies across S

etc., and f(S

) lies across S

, then we conclude that f

) lies across S

,andby

Theorem 5.10, there is a ﬁxed point of f

in S

. The orbit of this point travels

through all of the S

, so there is a ﬁxed point of f

in each of the S

Corollary 5.13 Let f be a map and 兵S

,...,S

其 be rectangular sets in

⺢

such that f(S

) lies across S

i⫹1

for 1 ⱕ i ⱕ k ⫺ 1andf(S

) lies across S

,all

with the same orientation. Then f

has a ﬁxed point in S

5.5 MARKOV PARTITIONS

We are now ready to update our deﬁnition of covering partition from Chapter 3

to two-dimensional maps. Let f be a one-to-one map of ⺢

Deﬁnition 5.14 Assume that S

,...,S

are rectangular subsets of a rect-

angle S whose interiors do not overlap. For simplicity we will assume that the

rectangles are formed from segments parallel to the coordinate axes and that the

map f stretches the rectangles in the direction of one axis and contracts in the

direction of the other. Assume that whenever f(S

) intersects S

in a set of nonzero

area, f(S

) “lies across S

” so that stretching directions are mapped to stretching

directions, and shrinking directions to shrinking directions. Then we say that

兵S

,...,S

其 is a Markov partition of S for f.

212

5.5 MARKOV PARTITIONS

Corollary 5.13 gives a way of constructing ﬁxed points from symbol se-

quences of Markov partitions. We can deﬁne itineraries of an orbit by assigning a

symbol to each subset in the Markov partition and tracing the appearances of the

orbit in these subsets. To illustrate this idea, we return to the skinny baker map.

E XAMPLE 5.15

The skinny baker map B in (5.1) has a Markov partition of the unit square

consisting of two rectangles L and R. It is clear from Figure 5.11 that L maps across

L and R vertically under the map B, and similarly for R.

We will construct itineraries for the points in the unit square that belong

to the invariant set of B; that is, those points whose forward iterates and inverse

images all lie in the unit square. In Example 5.3 we denoted the invariant set

by A.

In contrast to one-dimensional Markov partitions, the itineraries for the

skinny baker map B are “bi-inﬁnite”; that is, they are deﬁned for ⫺

⬁

⬍ i ⬍

⬁

.The

itinerary of a point v ⫽ (x

) is a string of subsets from the Markov partition

⭈⭈⭈S

⫺2

⫺1

•

⭈⭈⭈,

where the symbol S

is deﬁned by B

(v) 僆 S

.NotethatB is one-to-one, so that

⫺1

is deﬁned on the image of B, and in particular for the invariant set A of the

square S. We will form itineraries only for points that lie in the invariant set A

0 0 1

1/3

2/3

1/2

L R

B(L)

B(R)

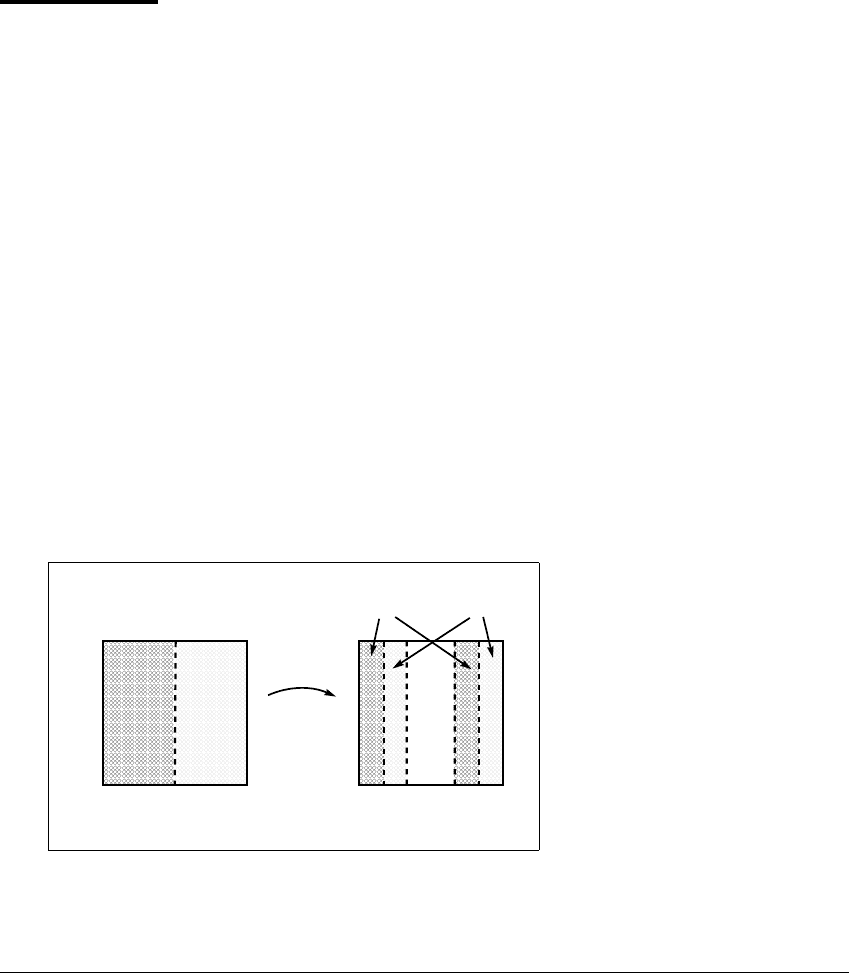
Figure 5.11 A Markov partition of the skinny baker map.

The partition consists of the left and right halves of the unit square. The center

third of the square has no pre-images.

213

C HAOS IN T WO-DIMENSIONAL M APS

of the map B; these points have inverse images B

⫺i

(v) for all i. Note also that

⫺i

(v)isinS

if and only if v is in B

To see what itineraries look like, we ﬁrst investigate the right-hand side

of the decimal point. Figure 5.12(a) shows the subsets of the unit square that

begin with

•

L and

•

R, respectively. The lower half is denoted

•

L because after one

iteration of B, those points all land in the left half of the square. The

•

L rectangle

is divided into

•

LL and

•

LR in Figure 5.12(b), separating the points in the lower

half of

•

L, which map to the left side after two iterations from the points of the

upper half of

•

L, which map to the right after two iterations. Further subdivisions,

which track the third iterate of B, are displayed in Figure 5.12(c).

We can already see the use of Markov partitions for locating periodic points

of B. For example, the strip marked

•

LL in Figure 5.12 must contain a ﬁxed point,

as does

•

RR, because of the repeated symbol. (The ﬁxed points are (0, 0) and

(1, 1), respectively.)

✎ E XERCISE T5.6

Find the (x

)-coordinates of the period-two orbits in the strips

•

LRL

and

•

RLR of Figure 5.12. Are there any other period-two orbits?

Figure 5.13 shows the forward images of the unit square under the map B.

Figures 5.13(a)-(c) show the images of B, B

,andB

, respectively. The part of the

1/2

.RR

.RL

.LR

.LL

1/2

.RRR

.RRL

.RLR

.RLL

.LRR

.LRL

.LLR

.LLL

(a) (b) (c)

Figure 5.12 Forward itineraries of points of the unit square under the skinny

baker map.

The unit squares in (a), (b), and (c) show successive reﬁnements of regions deﬁned

by itineraries. The points in

•

RLR, for example, map to the right half under B,the

left half under B

, and the right half under B

214

5.5 MARKOV PARTITIONS

1/3 2/3

L. R.

1/3 2/3

LL. RL. LR. RR.

1/3 2/3

RRL.

LRL.

(a) (b) (c)

Figure 5.13 Backward itineraries of points of the unit square under the skinny

baker map.

Each point p in RRL

•

, for example, satisﬁes p is in L, p is in B(R), and p is in B

(R).

itinerary to the left of the decimal point shows the inverse image history of that

point. For example, consider a point lying in the vertical strip denoted by RRL.

Reading symbols from right to left, the point lies in L, it is the iterate of a point

in R, and it is the second iterate of a point p

in R. (The reader is encouraged

to choose a point in RRL

•

and determine p

and p

visually.)

It is clear from Figure 5.12 that the horizontal strip represented by

•

⭈⭈⭈S

has width 2

⫺k

. An inﬁnite sequence

•

⭈⭈⭈ corresponds to a single hori-

zontal line. Similarly, Figure 5.13 shows that the points with symbol sequence

⫺k

⭈⭈⭈S

⫺1

•

form a vertical strip of width 3

⫺(k⫹1)

, and any particular inﬁnite

sequence extending to the left corresponds to a single vertical line of points.

✎ E XERCISE T5.7

Construct the periodic table for the skinny baker map, for periods up to 6.

Putting these facts together, we see that each bi-inﬁnite sequence of symbols

is owned by a single point in the unit square. So the itinerary of a point in the

invariant set A gives us a good address to identify that point. The correspondence

between bi-inﬁnite sequences and points in A is not quite one-to-one, since some

sequences identify the same point. For example,

•

RL and L

•

LR both identify the

point (0, 1 2).

215