Алексеев В.В. Физическое и математическое моделирование экосистем

Подождите немного. Документ загружается.

Так

как при больших массах М^ величина М

приближенно

равна M

/(2 + 712/Р), a coo пропорциональна УМ

, с увеличением

амплитуда колебаний жертв растет пропорционально М

, хищ-

ников

— пропорционально УМ

. Колебания биомасс хищников

отстают от колебаний биомасс жертв на 90°, колебания биомасс

жертв сдвинуты по фазе на

угол,

близкий к 180°.

Случай произвольных значений параметров хотя и может быть

рассчитан, но

дает

очень громоздкие выражения для амплитуды

колебаний.

Результаты интегрирования модели

(5.44)

на ЭВМ

области автоколебаний (методом Рунге — Кутта [74]) приве-

дены на рис. 5.19. Аналогичные колебания были получены и для

ПЯТИВИДОРОЙ

системы (см. табл. 5.1,

структура

7) [62].

5.5.2.

Автостохастический

режим

замкнутой

четырехвидовой

экосистеме

Одним из сравнительно недавних открытий в качественной

теории дифференциальных уравнений явилось установление факта,

что в некоторых детерминированных динамических системах на-

блюдается стохастическое поведение траекторий, несмотря на от-

сутствие внешних случайных воздействий.

Подобно

тому как предельный цикл в фазовом пространстве

динамической

системы является образом периодических автоколе-

баний,

так и хаотическое притягивающее множество — «странный

аттрактор», на котором все траектории неустойчивы и

ведут

себя

сложно и запутанно, — является математическим образом

стоха-

стических автоколебаний. В настоящее время «странные аттрак-

торы»

обнаружены в динамических моделях с нелинейными взаи-

модействиями достаточно простого вида, используемых в метеоро-

логии,

нелинейной оптике, радиофизике и т. д. [65, 97, 140, 148].

В природных экосистемах возможная стохастичность поведе-

ния

обычно затушевана множеством случайных воздействий. Од-

нако

лабораторные эксперименты [265, 291, 292, 300] показали,

что и в специально созданных постоянных условиях среды обита-

ния

некоторые популяции демонстрируют режим стохастических

автоколебаний. Наиболее часто стохастичность обнаруживается

системах с выраженной возрастной структурой популяций, что

связано

с существованием запаздывания в отклике на изменения

во внешней среде (см. гл. 6). Примером поддержания стохастиче-

ских автоколебаний в системе без возрастной структуры (сооб-

щество микроводорослей) может служить экспериментальная си-

стема, созданная и исследованная Рингельбергом [291, 292].

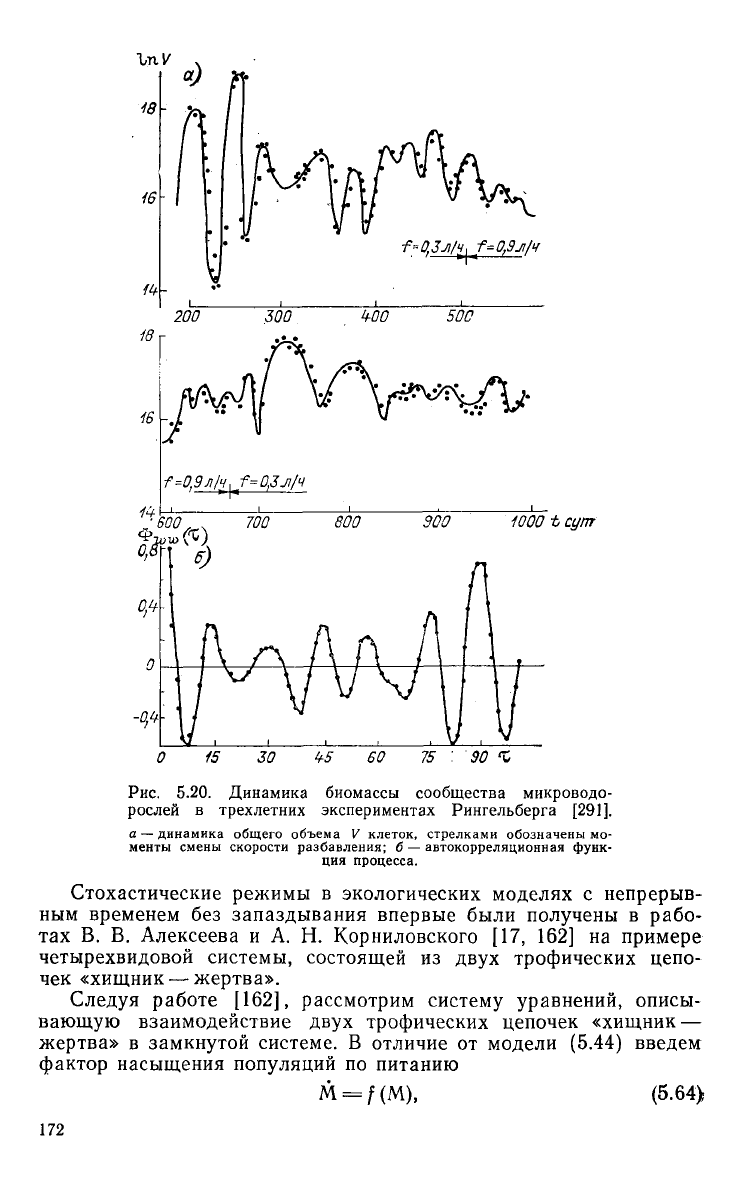
В установке, схема которой приведена на рис. 5.20 а, сообщество,

состоящее из семи видов микроводорослей, существовало более

трех

лет. Динамика общей биомассы водорослей и автокорреля-

ционная

функция процесса показаны на рис. 5.20 б, в. Несмотря

на

строго постоянные условия эксперимента, в системе наблюда-

лись стохастические автоколебания с периодом около 45 суток.

171

1000 t

cynr

Рис.

5.20. Динамика биомассы сообщества микроводо-

рослей в трехлетних экспериментах Рингельберга [291].

—

динамика общего объема

клеток, стрелками обозначены

мо-

менты смены скорости разбавления;

б —

автокорреляционная функ-

ция

процесса.

Стохастические режимы

экологических моделях

непрерыв-

ным

временем

без

запаздывания впервые были получены

рабо-

тах

В. В.

Алексеева

и А. Н.

Корниловского

[17, 162] на

примере

четырехвидовои системы, состоящей

из

двух

трофических цепо-

чек «хищник

—жертва».

Следуя работе [162], рассмотрим систему уравнений, описы-

вающую взаимодействие

двух

трофических цепочек «хищник

—

жертва»

замкнутой системе.

отличие

от

модели

(5.44)

введем

фактор насыщения популяций

по

питанию

= /

(М),

(5.64)

172

где

М = {М

;

}, f = {ft), i=Tl,

Л = -е,М,

M,M

/(l + аМ.) + PM,S/(1 + bS),

fi= — e

4-Y2M,M

/(l +aM,) Y2

Yi.

-eiM

YiM

/(l

+ а'м

) +

piM

S/(l

+ b's),

—E2M

+ Y2M

/(l

а'Мз), Y2

y'u

(

- + S = M

= const > 0

(b,

b' и а,

а' — константы полунасыщения соответственно для

жертв и хищников).

Исследуем условия существования

устойчивости стационар-

ного состояния системы (5.64),

котором биомассы

всех

видов

отличны от нуля (положительны).

Фазовое пространство системы

(5.64)

ограничено

представ-

ляет собой четырехмерную пирамиду, образованную координат-

ными

гиперплоскостями Mi = 0 (г

4) и

гиперплоскостью

0. Фазовые траектории никогда не пересекают ограничиваю-

щие

гиперплоскости

определены, таким образом, при любых

/е(0,

сю). На координатных гиперплоскостях всегда

существуют

стационарные точки, но они не

будут

рассматриваться, так как

попадание

них фазовых траекторий соответствует вымиранию

одного из видов.

Введем безразмерные параметры

а = ае

Д>2, а' = а

/^2,

(5.65)

Будем

считать,

что 6'

б.

Для

случая

координаты

стационарной

точки

опреде-

ляются

выражениями

п —

bKE+H(l-6)+K-^

~~ а(1-а)

2ЬКН

(5.66)

KQj-(y-6)/b

Г)

Чз

а'

(1-а')

К'

где

(l_

)/p,

/('=

;(l-a')/p\

Е = М

+ (6'

Ь)1ЬК'.

Я = 1 + К/К',

= {[ЬКЕ — Н (1

К]

+ АК

ЬЕ + 4КНЪ}''\

173

Стационарная

точка

(5.66)

положительно определена, если выпол-

няются

следующие условия для коэффициентов:

а>0,

(5.67)

кр—

(I-a)

a'{l—a')

YI^C—

)

ft'(1—6')

Устойчивость стационарного решения определяется величиной соб-

ственных значений оператора линеаризации df =

^гт- .(Q) }• Ха-

рактеристическое уравнение для определения собственных чисел

X имеет вид полинома четвертого порядка

det

П (X) = X* -

Х + «4 =

(5.68)

где

—

X D

—X

•

Л*

—Я,

D =

-via/a

- PQ,S, R = y\a (l - a') Q

- Y'QSS,

p =

(1 —

Z = yW/a —

V =

(\-

a')

S=l

вопрос об устойчивости определяется условиями Раусса — Гур-

вица:

(i = 171),

—

aia

— аз > 0.

(5.69)

Коэффициент

положителен всегда. Можно показать, что при

выполнении

неравенства

a(l-a) + a'(l-a')

коэффициент

аг отрицателен, и, следовательно, устойчивость ста-

ционарного

решения нарушается. При больших M

условие

Й1

>0 в пространстве параметров возможно лишь в тонком ци-

линдре, параллельном оси M

и содержащем ее. Площадь его се-

чения

стремится к нулю при M

-*-oo.

174

Более детально условия устойчивости

(5.69)

были проанали-

зированы

на ЭВМ. Для

упрощения исследования значения

неко-

торых параметров были зафиксированы:

Ё2

= а' =

= V.

Условия существования положительного стационарного реше-

ния

(5.66)

этом

случае

при-

обретают

вид

< 1/2, М

> 3Q./2 + 2Q

где

Условие

чивости

нарушения

устой-

(5.70)

может быть

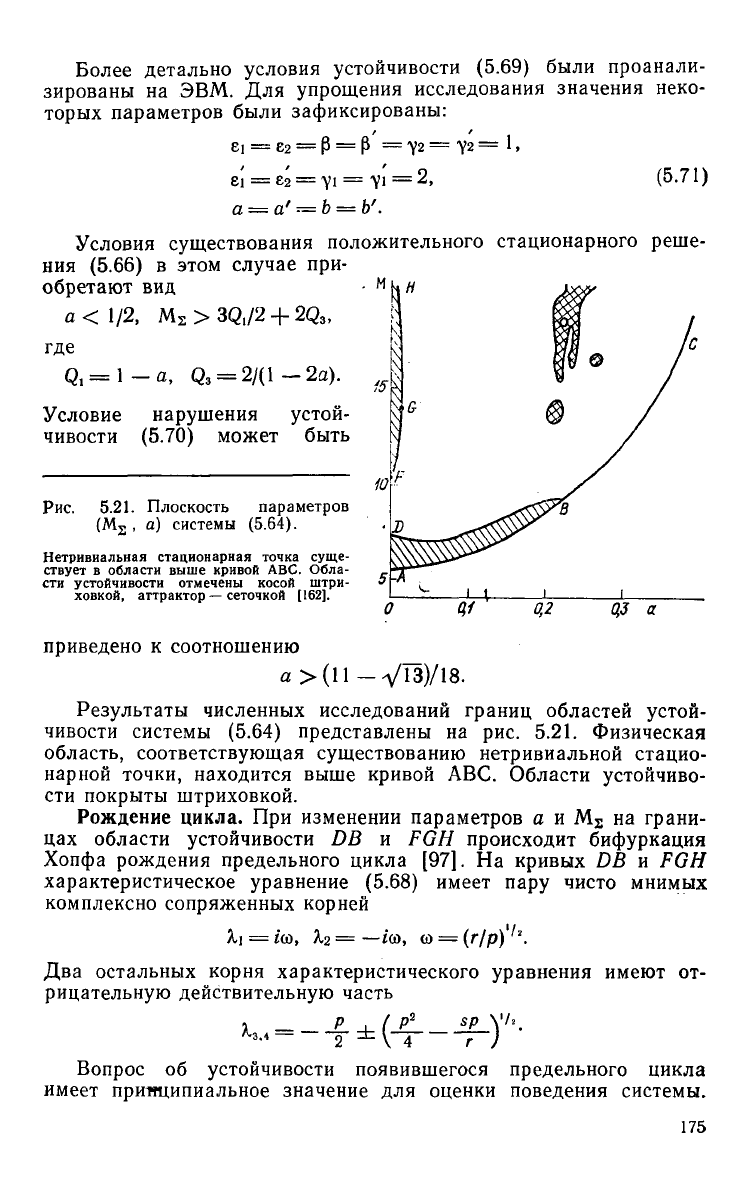
Рис.

5.21. Плоскость параметров

, а) системы (5.64).

Нетривиальная

стационарная точка суще-

ствует

области выше кривой

ABC.

Обла-

сти устойчивости отмечены косой штри-

ховкой, аттрактор

—

сеточкой [162].

приведено

соотношению

>(11 -VW18.

Результаты численных исследований границ областей устой-

чивости системы

(5.64)

представлены

на рис. 5.21.

Физическая

область, соответствующая существованию нетривиальной стацио-

нарной

точки, находится выше кривой

ABC.

Области устойчиво-

сти покрыты штриховкой.

Рождение

цикла. При

изменении параметров

а и M

на

грани-

цах области устойчивости

DB и FGH

происходит бифуркация

Хопфа рождения предельного цикла

[97]. На

кривых

DB и FGH

характеристическое уравнение

(5.68)

имеет пару чисто мнимых

комплексно

сопряженных корней

Я.]

го»,

—/со, со

(rip)'''.

Два остальных корня характеристического уравнения имеют

от-

рицательную действительную часть

Лз.4

— - -J- ± ^"4

—

Вопрос

об

устойчивости появившегося предельного цикла

имеет принципиальное значение

для

оценки поведения системы.

175

Если

порожденный предельный цикл окажется неустойчивым,

фазовые траектории

будут

уходить

от равновесия, и при ограни-

ченном

фазовом пространстве движение становится запутанным.

Устойчивость предельного цикла можно определить по знаку так

называемого коэффициента Ляпунова L [38]. При L отрицатель-

ном

предельный цикл является устойчивым, при L положитель-

ном

— неустойчивым.

Для системы уравнений стандартного вида

Xi =

+£

iik

XjX

+ £

XjX

+ ....

(5.72)

/. k i, к. i

точке бифуркации коэффициент L вычисляется по формуле,

предложенной Неймарком [38]:

L = 3 (а

ш2

2i)

— 2/

(а

212

222

—

п2

и1

)/ф

—

— 2 X {2аш

{п22к

+ айн) X

(А* — 2ш) +

4со

)}

(коэффициенты

а,-,•*,

ацы предполагаются симметричными).

Сведение системы

(5.64)

к стандартному виду

(5.72)

можно

осуществить с помощью линейного преобразования координат, при

котором характеристическая матрица П(Х) системы линейных

уравнений для определения устойчивости становится диаго-

нальной.

Нетрудно видеть, что правый верхний минор третьего порядка

матрицы П (X) (см. (5.68))

D А А

det

-X О О

В R — X Z

является базисным и отличен от нуля при любых значениях па-

раметров и любых характеристических числах, удовлетворяющих

характеристическому уравнению. При построении вектора диаго-

нализации

е(Х) первая координата может быть выбрана произ-

вольно,

е(к) имеет вид

+ X), PA(Z-R + X),

+ X (АВ — CZ) — s/V, Ve

(X)/X}.

Матрица T=

{e(Xi)}

определяет необходимую замену переменных

М,=

ZjlXi

+ Qt,

(5.73)

сводящую систему

(5.64)

к стандартной форме (5.72). Таким об-

разом, хотя вычисление коэффициента Ляпунова L достаточно

176

громоздко,

оно

сводится

конечному числу алгебраических

опе-

раций.

Численное

определение коэффициента Ляпунова

для

границ

устойчивости

DB и FGH

показало,

что L на них

отрицательно

(рис.

5.22),

поэтому

зонах неустойчивости вблизи границ

ста-

ционарная

точка

плавно переходит

малый устойчивый

пре-

дельный цикл.

Переход

к стохастическим колебаниям.

Удаление

от

бифурка-

ционных

кривых

DB и FGH со-

провождается ростом предель-

ного цикла.

Для

рассматривае-

мой

системы можно оценить

мак-

симально возможные размеры

аттрактора.

Поскольку

фазовый объем

си-

стемы представляет собой четы-

рехмерную пирамиду, естественно

аппроксимировать аттрактор

пло-

скостями,

параллельными

гра-

ницам.

Можно показать,

что

cr-fO

Рис.

5.22.

Значения

коэффициента

Ляпу-

нова

на

границах областей устойчивости

(а) и FGH (б).

-ЛР-

предельный цикл может увеличиваться только

пределах плоскостей

I»

= М' =

М^

— AM,

1=1

M'-Q

ДМ

min (6/6(1

—

6),

b'lb'(\—

(5.74)

Границы

аттрактора образуют замкнутую поверхность, которую

траектории пересекают только

направлении вовнутрь.

Дальнейшее изменение параметра

ведет

изгибу предель-

ного цикла

и его

бифуркации. Вблизи области, заштрихованной

«сеточку»

на рис. 5.21,

наблюдались серии бифуркаций

удвое-

ния

периода:

определенном интервале значений параметра

период процесса составлял

Т; в

некотором новом интервале

зна-

чений

а — 27, в

следующем интервале

— 4Г и т. д.,

причем интер-

вал значений параметра,

котором период составлял

2пТ,

с ростом

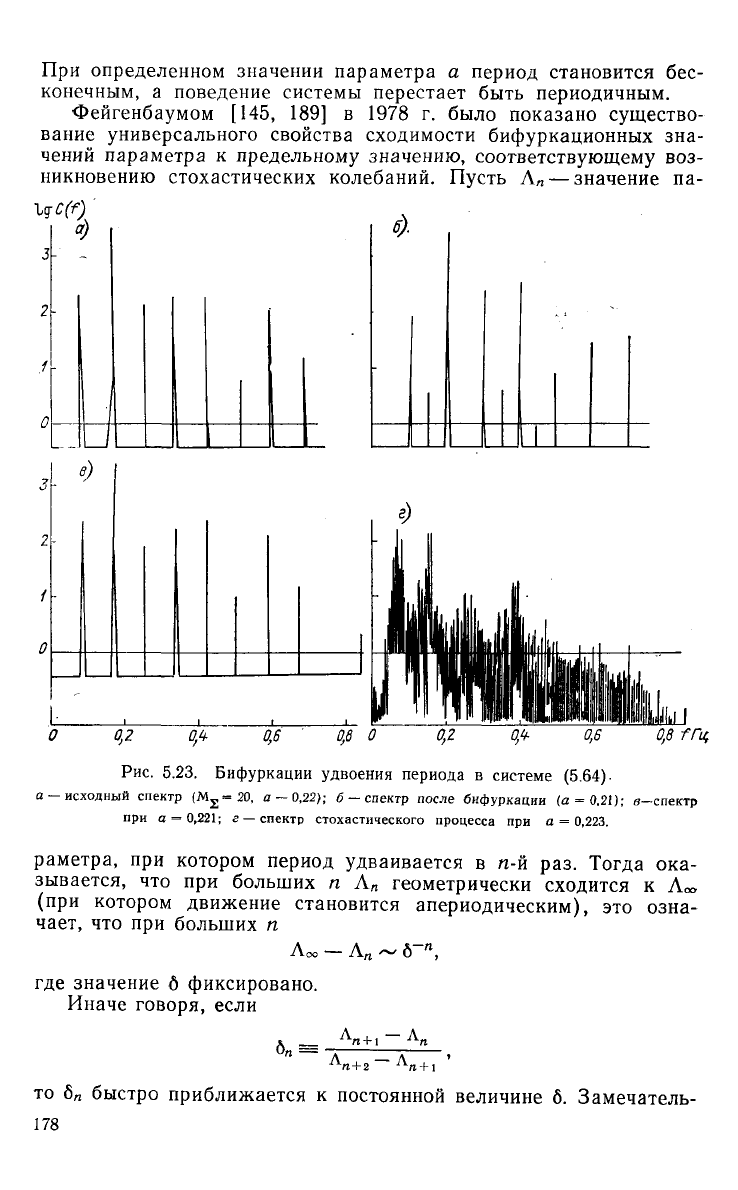
уменьшался. Спектры последовательных бифуркаций

при

переходе

стохастическому режиму показаны

на рис. 5.23.

12 Заказ

№ 57

177

При

определенном значении параметра а период становится бес-

конечным,

а поведение системы перестает быть периодичным.

Фейгенбаумом [145, 189] в 1978 г. было показано существо-

вание универсального свойства сходимости бифуркационных зна-

чений

параметра к предельному значению, соответствующему воз-

никновению

стохастических колебаний. Пусть Л„ — значение па-

c(fY

0,2 0,6

Рис.

5.23. Бифуркации удвоения периода в системе (5.64)-

—исходный спектр (М

=20, а —

0,22);

б — спектр после бифуркации (а -

0,21);

в—спектр

при а = 0,221; г — спектр стохастического процесса при а = 0,223.

раметра, при котором период удваивается в п-й раз. Тогда ока-

зывается, что при больших п А

геометрически сходится к Лоо

(при

котором движение становится апериодическим), это озна-

чает, что при больших п

Лоо — Л„ ~ Ь~

где значение 6 фиксировано.

Иначе

говоря, если

6„

то б„ быстро приближается к постоянной величине б. Замечатель-

178

ным

является то, что у

всех

систем, испытывающих удвоение

периода, значение б одинаково и равно универсальному числу

[145, 189]:

4,6692016....

Для системы

(5.64)

константа Фейгенбаума рассчитывалась

при

= 14,0; бифуркации наблюдались для следующих значе-

ний

о: oi =

0,223

±5-Ю-

;

= 0,218 ± 5- 1Q-

; о

0,21774

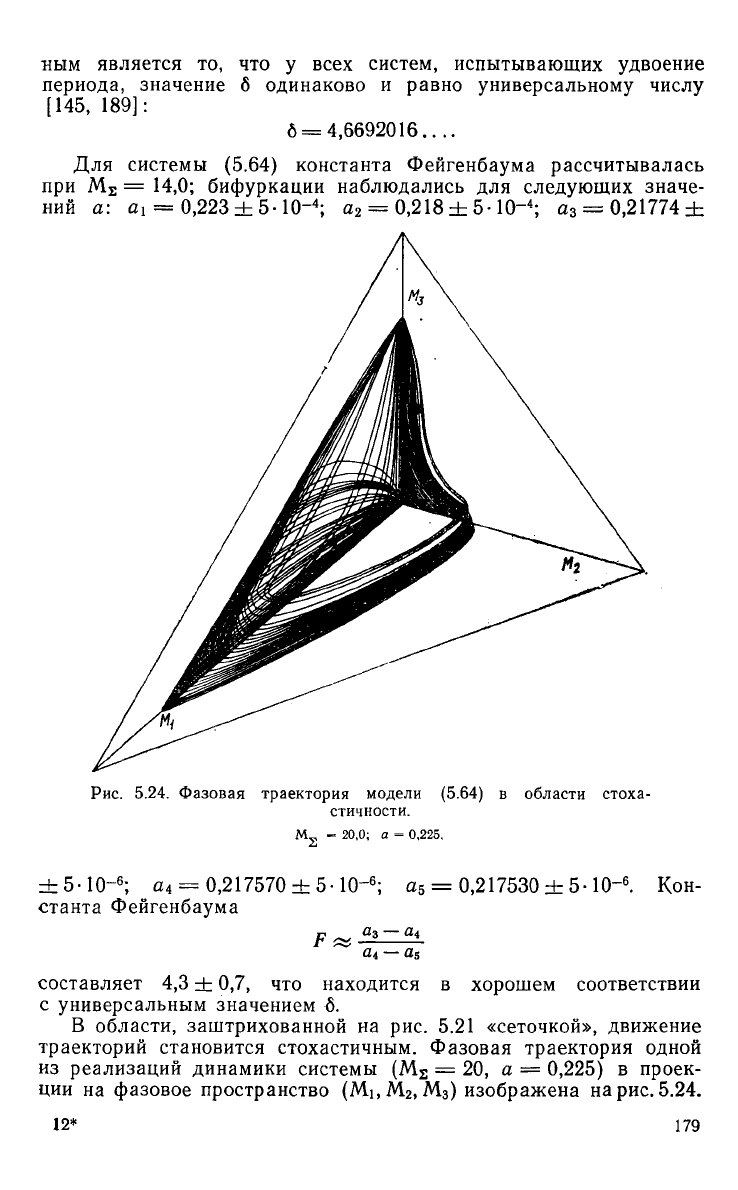
Рис.

5.24.

Фазовая

траектория модели (5.64) в области стоха-

стичности.

20,0; а = 0,225.

±5-Ю-

;

0,217570

±5-Ю-

;

станта Фейгенбаума

0,217530

±5-Ю-

Кон-

составляет 4,3 ± 0,7, что находится в хорошем соответствии

с универсальным значением б.

В области, заштрихованной на рис. 5.21 «сеточкой», движение

траекторий становится стохастичным. Фазовая траектория одной

из

реализаций динамики системы (M

= 20, а =

0,225)

в проек-

ции

на фазовое пространство (Mi,M

, М

) изображена на рис. 5.24.

12*

179

Наиболее распространенным способом выявления стохастич-

ности

в системе является анализ спектров процесса. Как известно,,

периодические процессы в модельных динамических системах ха-

рактеризуются дискретным спектром с распределением мощности

сигнала по одной или нескольким частотам. При переходе к сто-

*l U

100

200

300

WO., t

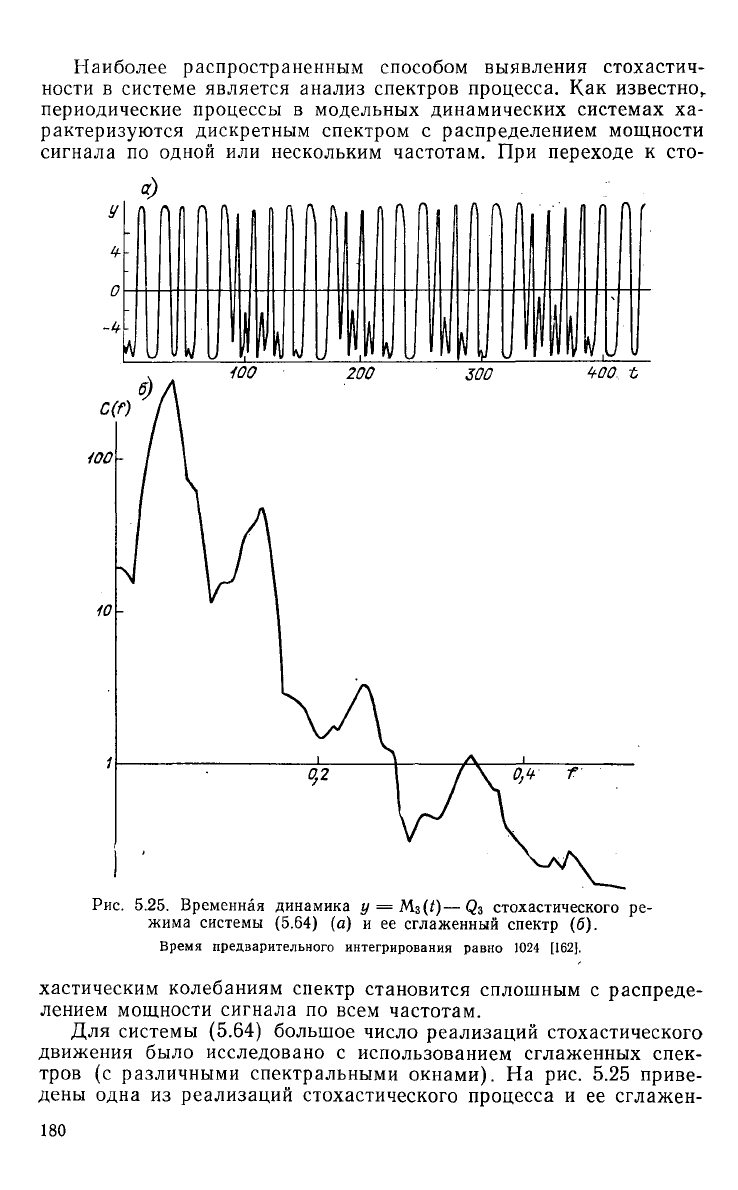
Рис.

5.25. Временная динамика у =

(t)—Q

стохастического ре-

жима системы

(5.64)

(а) и ее сглаженный спектр (б).

Время предварительного интегрирования равно

1024

[162].

хастическим колебаниям спектр становится сплошным с распреде-

лением мощности сигнала по всем частотам.

Для системы

(5.64)

большое число реализаций стохастического

движения было исследовано с использованием сглаженных спек-

тров (с различными спектральными окнами). На рис. 5.25 приве-

дены одна из реализаций стохастического процесса и ее сглажен-

180