Алексеев Г.В. Классические методы математической физики. Часть 2
Подождите немного. Документ загружается.


u r t
ϕ
0
ϕ
1
θ
u|
t=0
= ϕ
0
(r),
∂u
∂t
t=0
= ϕ
1
(r), 0 ≤ r < R.
ϕ
0
ϕ
1
[0, R)
u θ
1
a
2
∂
2
u
∂t
2
=
∂
2
u
∂r
2
+
1
r
∂u
∂r
.
u(r, t) = w(r)T (t).
T
′′
(t)
a
2
T (t)
=
w
′′
(r) +
1
r
w
′
(r)
w(r)
= −λ
2
.
λ
2
T w
T
′′
(t) + λ
2
a
2
T (t) = 0,
w
′′
(r) +
1
r
w
′
(r) + λ
2
w(r) = 0.
w
w(R) = 0.
λ
2
u
r = R
ν = 0 ν
W
′′
(r) +
1
r
W
′
(r) +
λ
2
−
ν
2
r
2
W (r) = 0.

J
ν
(λr)
N
ν
(λr)
H
(1)
ν
(λr) = J
ν
(λr) + iN
ν
(λr), H
(2)
ν
(λr) = J
ν
(λr) − iN
ν
(λr).
J
ν
λr N
ν
r = 0
H
(1)
ν
H
(2)
ν
r = 0
r = 0
u
Ω r = 0
J
0
(λr) N
0
(λr)
r = 0
|w(0)| < ∞,
r = 0
w(r) = C
1
J
0
(λr) + C
2
N
0
(λr),
C
1
C
2
C
2
= 0 C
2
= 0
C
1
6= 0
J
0
(λR) = 0 .
λR = µ
J
0
(µ) = 0.
sinµ = 0
µ
n

0 < µ
1
< µ
2
< ... < µ
k
< ... , lim
k→∞
µ
k
= ∞.
µ
k
λ
2
k
w
k
λ
2
k
=
µ
k
R
2
, w
k
(r) = J
0
µ
k
r
R
, k = 1, 2, 3, ... .
J
0
(µ
k
r/R)
sinµ
k
x
w
k
L
2
r
(0, R) L
2
r
(0, R)
(w, v) ≡
R
Z
0
w(r)v
∗
(r)rdr ∀w, v ∈ L
2
r
(0, R).
∗
(w
k
, w
l
) ≡
R
Z
0
J
0
µ
k
r
R
J
0
µ
l
r
R
rdr =
1
2
R
2
J
2
1
(µ
k
), k = l,
0, k 6= l.
J
1
{w
k
}
∞
k=1
L
2
r
(0, R)
λ
2
k
w
k
λ = λ
k
= µ
k
/R
T
k
(t) = a
k
cos
aµ
k
t
R
+ b
k
sin
aµ
k
t
R
,
a
k
b
k
u
k
(r, t) =
a
k
cos
aµ
k
t
R
+ b
k
sin
aµ
k
t
R
J
0
µ
k
r
R

k
u(r, t) =
∞
X
k=1
a
k
cos
aµ
k
t
R
+ b
k
sin
aµ
k
t
R
J
0
µ
k
r
R
t Q
T
r t Q
T
a
k
b
k
∂u
∂t
=
∞
X
k=1
aµ
k
R
b
k
cos
aµ
k
t
R
− a
k
sin
aµ
k
t
R
J
0
µ
k
r
R
,
t
ϕ
0
(r) =
∞
X
k=1
a
k
J
0
µ
k
r
R
, ϕ
1
(r) =
∞
X
k=1
aµ
k
R
b
k
J
0
µ
k
r
R
.
ϕ
0
ϕ
1
L
2
r
(0, R)
w
k
a
k
b
k
ϕ
0
ϕ
1
rJ
0
(µ
k
r/R) (0, R)
a
k
=
2
R
2
J
2
1
(µ
k
)
R
Z
0
rϕ
0
(r)J
0
µ
k
r
R
dr, b
k
=
2
aµ
k
RJ
2
1
(µ
k
)
R
Z
0
rϕ
1
(r)J
0
µ
k
r
R
dr.
a
k
b
k
u(r, t) =
∞
X
k=1
α
k
J
0
µ
k
r
R
sin
aµ
k
t
R
+ ϕ
k
.

u
k
(r, t) = α
k
J
0
µ
k
r
R
sin
aµ
k
t
R
+ ϕ
k
.
(r, θ) Ω
ω
k
T
k
ω
k
=
aµ
k
R
=
µ
k
R
s
T
ρ
, T
k
=
2π
ω
k
=
2πR
aµ
k
,
ϕ
k
A
k
(r) = a
k
J
0
(µ
k
r/R)
r = r
0
J
0
µ
k
r
0
R
= 0,
A
k
k
k = 1 k = 2 k = 3
J
0
Ω

(0, l) R
R
2
ω
S a
∆u + k
2
u = 0
D S
αu + β
∂u
∂n
S
= g
S
u(x) = O(|x|
−1
),
∂u(x)
∂|x|
− iku(x) = o(|x|
−1
)
|x| → ∞.
k = ω/c ω c = const
α, β g S g
S α β
α = 1, β = 0
S α = 0, β = 1
S

r, θ, ϕ
∂
∂r
r
2
∂u
∂r
+ ∆
θ,ϕ
u + k
2
r
2
u = 0,
∆
θ,ϕ
u =
1
sinθ
∂
∂θ
sinθ
∂u
∂θ
+
1
sin
2
θ
∂
2
u
∂ϕ
2
.
u(r, θ, ϕ) = R(r)v(θ, ϕ).
(r
2
R
′
)
′
+ k
2
r
2
R
R
= −
∆
θ,ϕ
v
v
= λ,
λ
(r
2
R
′
)
′
+ (k
2
r
2
− λ)R = 0
R
∆
θ,ϕ
v + λv ≡
1
sinθ
∂
∂θ
sinθ
∂v
∂θ
+
1
sin
2
θ
∂
2
v
∂ϕ
2
+ λv = 0
v
C
∞
(S
1
)
S
1
= {(r, θ, ϕ), r = 1, 0 ≤ θ ≤ π, 0 ≤ ϕ < 2π}
v(θ, ϕ + 2π) = v(θ, ϕ),
ϕ
1
sinθ
d
dθ
sinθ
dv
dθ
+ λv = 0, θ ∈ (0, π).

x = cosθ : [0, π] → [−1, 1], v(θ) = P (x),
d
dθ
=
dx
dθ
d
dx
= −sinθ
d
dx
, (4.11a)
d
dx
1 − x
2
dP
dx
+ λP = 0, x ∈ (−1, 1).
C
∞
[−1, 1]
λ = λ
n
≡ n(n + 1), n = 0, 1, 2, ... .
d
dx
1 − x
2
dP
dx
+ n(n + 1)P = 0, x ∈ (−1, 1)
P
n
(x)
P
n
(x)
P
n
(x) =
1
2
n
n!
d
n
dx
n
(x
2
− 1)
n
, n = 0, 1, ... .
P
n
(−x) = (−1)
n
P
n
(x)
{P
n
(x)}
∞
n=0
L
2
(−1, 1)
(P
n
, P
m
) =
1
Z
−1
P
n
(x)P
m
(x)dx =
2
2n+1
, n = m,
0, n 6= m.
P
0
(x) = 1, P
1
(x) = x, P
2
(x) =
1
2
(3x
2
− 1), P
3
(x) =
1
2
(5x
3
− 3x),
P
4
(x) =
1
8
(35x
4
− 30x
2
+ 3), P
5
(x) =
1
8
(63x
5
− 70x
3
+ 15x) .
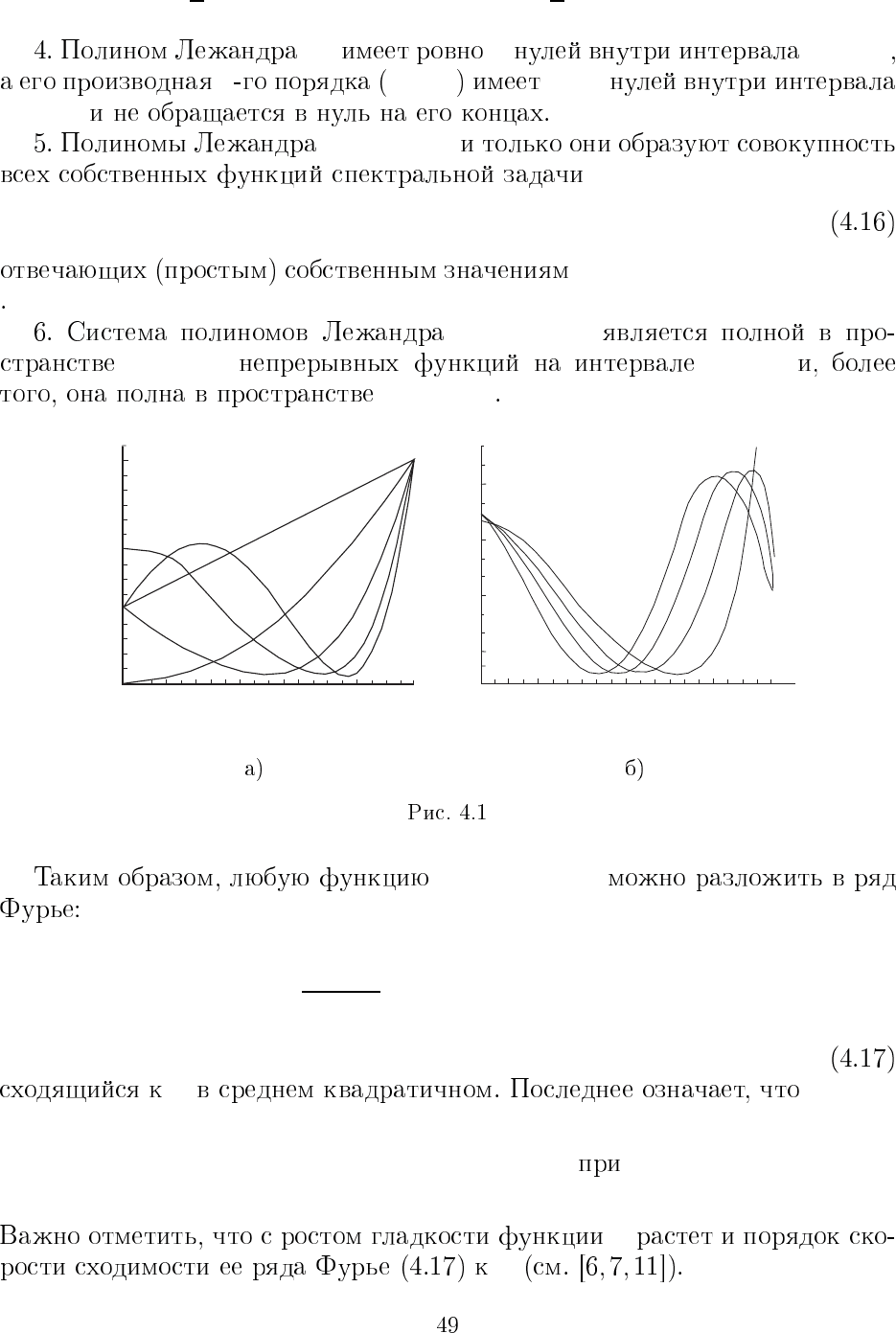
P
n
n (−1, 1)
k k ≤ n n−k
(−1, 1)
{P
n
(x)}
∞
n=0
[(1 − x
2
)P
′
]
′
+ λP = 0, P ∈ C
2
(−1, 1) ∩ C[−1, 1 ],
λ
n
= n(n+1), n = 0, 1, 2, ...
{P
n
(x)}
∞
n=0
C[−1, 1] [−1, 1]
L
2
(−1, 1)
x
P
x
P
0.1
0.2 0.3
0.4
0.5
0.6
0.7
0.8
0.9
1.0
-1.0
-0.8
-0.6
-0.4
-0.2
0
0.2
0.4
0.6
0.8
1.0
1.2
1.4
1.6
1.0
0.5
-0.5
0
0.5
1.0
f ∈ L
2
(−1, 1)
f(x) =
∞
X
n=0
a
n
P
n
(x), a
n
=
(f, P
n
)
kP
n
k
2
, (f, P
n
) =
1
Z
−1
f(x)P
n
(x)dx, kP
n
k
2
=
1
Z
−1
P
2
n
dx,
f
kf(x) −
N
X
n=0
a
n
P
n
(x)k
L
2
(−1,1)
→ 0
N → ∞.
f
f

v(θ, ϕ) = Q(θ)Φ(ϕ).
sin
2
θ
1
Qsinθ
d
dθ
sinθ
dQ
dθ
+ λ
= −
Φ
′′
Φ
= µ,
µ
1
sinθ
d
dθ
sinθ
dQ
dθ
+
λ −
µ
sin
2
θ
Q = 0
Q
Φ
′′
+ µΦ = 0
Φ
µ = m
2
, m = 1, 2, ... .
µ = m
2
Φ(ϕ) = acosmϕ + bsinmϕ,
a b
Q(θ) = P (cosθ) = P (x) ,
d
dx
(1 − x
2
)
dP
dx
+
λ −
m
2
1 − x
2
P = 0
(−1, 1).
[−1, 1]
m = 0
[−1, 1]
P
m
λ
v(θ, ϕ) = ( acosmϕ + bsinmϕ)P
m
λ
(cosθ)
