Alciatore D.G., Histand M.B. Introduction to Mechatronics and Measurement Systems

Подождите немного. Документ загружается.

Confirming Pages

Figure 6.4 AND realization schematic of the security system.

ABCD

6.7 Finding a Boolean Expression Given a Truth Table 211

Because there are a total of four AND gates and six inverters, the circuit can be

constructed with two ICs: one quad AND gate IC (e.g., the 7408), which contains

four AND gates, and one hex inverter IC (e.g., the 7404), which contains six inverters.

Equation 6.30 could also be implemented using two ICs because only two OR gates

and two AND gates are required. Therefore, for the security system, the all-AND

realization did not reduce the number of ICs. However, for more complex Boolean

expressions, a single-type gate realization will usually reduce the number of ICs.

The solution just presented is known as a hardware solution because it uses inte-

grated circuit gates to provide the desired logic. An alternative is to implement the

logic using a program running on a microcontroller. This solution, called a software

solution, is presented in Example 7.5 in Section 7.5.2.

■ CLASS DISCUSSION ITEM 6.3

Everyday Logic

Make a list of devices that you interact with on a daily basis that use logic for con-

trol purposes. For each, describe what logic is being performed.

6.7 FINDING A BOOLEAN EXPRESSION

GIVEN A TRUTH TABLE

As an alternative to the method presented in Sections 6.6.1 and 6.6.2 , where we

defined a logic problem in words and then wrote quasi-logic statements, sometimes

it is more convenient to express the complete input/output combinations with a truth

table. In these situations, there are two methods for directly obtaining the Boolean

expression that performs the logic specified in the truth table. Both methods are

described here, and an example is given to demonstrate their application.

alc80237_ch06_197-257.indd 211alc80237_ch06_197-257.indd 211 11/01/11 3:53 PM11/01/11 3:53 PM

Confirming Pages

212 CHAPTER 6 Digital Circuits

The first method is known as the sum-of-products method. It is based on the fact

that we can represent an output as a sum of products containing combinations of the

inputs. For example, if we have three inputs A, B, and C and an output X, the sum of

products would be a Boolean expression containing input terms AND-ed together to

form product terms that are OR-ed together to define the output X as a Boolean sum.

The following equation is an example of what a sum-of-products expression looks like:

XABC⋅⋅()ABC⋅⋅()ABC⋅⋅()++=

(6.34)

If we form a product for every row in the truth table that results in an output of

1 and take the sum of the products, we can represent the complete logic of the table.

For rows whose output values are 1, we must ensure that the product represent-

ing that row is 1. In order to do this, any input whose value is 0 in the row must be

inverted in the product. By expressing a product for every input combination whose

value is 1, we have completely modeled the logic of the truth table because every

other combination will result in a 0.

The second method is known as the product-of-sums method. It is based on

the fact that we can represent an output as a product of sums containing combina-

tions of the inputs. For example, if we have three inputs A, B, and C and an output X,

the product of sums would be a Boolean expression containing input terms OR-ed

together to form sum terms that are AND-ed together to define the output X as a

Boolean product. The following equation is an example of what a product-of-sums

expression looks like:

X ABC++()ABC++()ABC++()⋅⋅=

(6.35)

If we form a sum for every row in the truth table that results in an output of 0

and take the product of the sums, we can represent the complete logic of the table.

For rows whose output values are 0, we must ensure that the sum representing that

row is 0. In order to do this, any input whose value is 1 in the row must be inverted

in the sum. By expressing a sum for every input combination (row) whose value is 0,

we have completely modeled the logic of the truth table because every other combi-

nation will result in a 1.

In performing binary arithmetic, the simplest operation is summing the two least significant

bits resulting in a sum bit and a carry bit. The four possible combinations for adding two bits

are shown below.

0011A

+1 +0 +1 +B

0110

The last column shows the terminology used. The two input bits are labeled A and B, the

sum of the two bits is labeled S, and the carry bit, if there is one, is labeled C. Only in the last

case (1  1) is the carry bit 1; otherwise it is 0.

Sum of Products and Product of Sums

EXAMPLE 6.4

alc80237_ch06_197-257.indd 212alc80237_ch06_197-257.indd 212 11/01/11 3:53 PM11/01/11 3:53 PM

Confirming Pages

6.7 Finding a Boolean Expression Given a Truth Table 213

The truth table for this operation is

ABSC

0000

0110

1010

1001

We apply the sum-of-products and product-of-sums methods to both of the these outputs to

illustrate how the methods differ.

Using the procedure in the paragraph after Equation 6.34 , the sum-of-products method

applied to output S yields

SAB⋅()AB⋅()+=

The product (AND) terms represent rows two and three where S is 1.

Using the procedure in the paragraph after Equation 6.35 , the product-of-sums method

applied to output S yields

SAB+

()

AB+

()

⋅=

The sum (OR) terms represent rows one and four where S is 0.

The sum-of-products method applied to output C yields

CAB⋅

()

The product (AND) term represents row four where C is 1.

The product-of-sums method applied to output C yields

CAB+()AB+()AB+()⋅⋅=

The sum (OR) terms represent rows one, two, and three, where C is 0.

Note that the sum-of-products method was easier to apply to output C because only a

single row has an output of 1. You can verify all of the derived expressions by testing each

with a truth table, comparing the results to the desired truth table ( Question 6.29 ).

If we use the product-of-sums result for S and the sum-of-products result for C, we

obtain a circuit using the fewest number of gates:

This circuit is known as a half adder because it applies only to the two least significant bits

of a sum of two multiple-bit numbers. The higher-order bits require a lower-order carry bit

as an additional input, and the circuit is called a full adder (see Question 6.31 ).

alc80237_ch06_197-257.indd 213alc80237_ch06_197-257.indd 213 11/01/11 3:54 PM11/01/11 3:54 PM

Confirming Pages

Figure 6.5 Clock pulse edges.

logic

positive

edge

negative

edge

negative

edge

positive

edge

level: high

level: low

214 CHAPTER 6 Digital Circuits

An alternative to the sum-of-products and product-of-sums methods is Karnaugh

mapping. This method results in a simplified Boolean expression through truth table

manipulation. Internet Link 6.3 describes the method and provides examples.

6.8 SEQUEN TIAL LOGIC

Combinational logic devices generate an output based on the input values, inde-

pendent of the input timing. With sequential logic devices, however, the timing or

sequencing of the input signals is important. Devices in this class include flip-flops,

counters, monostables, latches, and more complex devices such as microprocessors.

Sequential logic devices usually respond to inputs when a separate trigger signal

transitions from one level to another. The trigger signal is usually referred to as the

clock (CK) signal. The clock signal can be a periodic square wave or an aperiodic

collection of pulses. Figure 6.5 illustrates edge terminology in relation to a clock

pulse, where an arrow is used to indicate edges where state transitions occur. Posi-

tive edge-triggered devices respond to a low-to-high (0 to 1) transition, and nega-

tive edge-triggered devices respond to a high-to-low (1 to 0) transition. This topic

is addressed again in Section 6.9.1 where it is applied to flip-flops.

6.9 FLIP-FLOPS

Because digital data is stored in the form of bits, digital memory devices such as

computer random access memory (RAM) require a means for storing and switch-

ing between the two binary states. A flip-flop is a sequential logic device that can

perform this function. The flip-flop is called a bistable device, because it has two

and only two possible stable output states: 1 (high) and 0 (low). It has the capability

to remain in a particular output state (i.e., storing a bit) until input signals cause it

to change state. This is the basis of all semiconductor information storage and pro-

cessing in digital computers; in fact, flip-flops perform many of the basic functions

critical to the operation of almost all digital devices.

Internet Lin

6.3Karnaugh

Mapping

■ CLASS DISCUSSION ITEM 6.4

Equivalence of Sum of Products and Product of Sums

Draw the logic circuits for S and C in Example 6.4 using only the product-of-sums

results and then do the same for the sum-of-products results. Compare your circuits

to the one shown in the example. Also, show that the sum-of-products and product-

of-sums results are equivalent.

alc80237_ch06_197-257.indd 214alc80237_ch06_197-257.indd 214 11/01/11 3:54 PM11/01/11 3:54 PM

Confirming Pages

6.9 Flip-Flops 215

A fundamental flip-flop, an RS flip-flop, is schematically shown in Figure 6.6 .

S is the set input, R is the reset input, and Q and Q are the complementary outputs.

Most flip-flops include both outputs, where one output is the inverse (NOT) of the

other. The RS flip-flop operates based on the following rules:

1 . As long as the inputs S and R are both 0, the outputs of the flip-flop remain

unchanged.

2 . When S is 1 and R is 0, the flip-flop is set to Q  1 and Q  0.

3 . When S is 0 and R is 1, the flip-flop is reset to Q  0 and Q  1.

4 . It is “not allowed” (NA) to place a 1 on S and R simultaneously because the

output will be unpredictable.

A truth table is a valuable tool for describing the functionality of a flip-flop.

The truth table for a basic RS flip-flop is given in Table 6.4 . The first row shows the

memory state where the flip-flop retains the last value set or reset. Q

is the value of

the output Q before the indicated input conditions were established; 1 is logic high

and 0 is logic low. The NA in the last row indicates that the input condition for that

row is not allowed. Because we are precluded from applying the S  1, R  1 input

condition, the RS flip-flop is seldom used in actual designs. Other more versatile

flip-flops that avoid the NA limitation are presented in subsequent sections.

To understand how flip-flops and other sequential logic circuits function, we

will look at the internal design of an RS flip-flop illustrated in Figure 6.7a. It consists

of combinational logic gates with internal feedback from the outputs to the inputs

of the NAND gates. Figure 6.7b illustrates the timing of the various signals, which

are affected by very short propagation delays through the NAND gates. Immediately

after signal R transitions from 0 to 1, the inputs to the lower NAND gate are 0 and Q,

which is still 1. This changes Q to 1 after a slight propagation delay Δ t

. Feedback of

Q to the top NAND gate drives Q to 0 after a slight delay Δ t

. Now the flip-flop is

Figure 6.6 RS flip-flop .

Table 6.4 Truth table for the RS flip-flop

Inputs Outputs

SRQ Q

101 0

010 1

11 NA

alc80237_ch06_197-257.indd 215alc80237_ch06_197-257.indd 215 11/01/11 3:54 PM11/01/11 3:54 PM

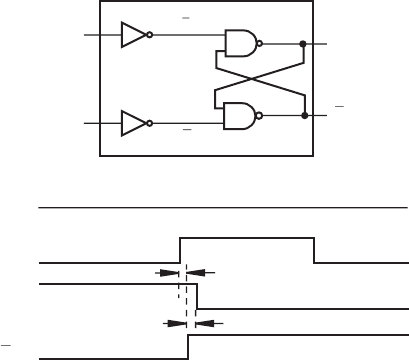
Confirming Pages

Figure 6.7 RS flip-flop internal design and timing.

(a) internal design

Δt

(b) timing diagram

216 CHAPTER 6 Digital Circuits

reset, and it remains in this state even after R returns to 0. The set operation functions

in a similar manner. The propagation delays Δ t

and Δ t

are usually in the nanosec-

ond range. All sequential logic devices depend on feedback and propagation delays

for their operation.

6.9.1 Triggering of Flip-Flops

Flip-flops are usually clocked; that is, a signal designated “clock” coordinates or

synchronizes the changes of the output states of the device. This allows the design

of complex circuits such as a microprocessor where all system changes are triggered

by a common clock signal. This is called synchronous operation because changes in

state are coordinated by the clock pulses. The outputs of different types of clocked

flip-flops can change on either a positive edge or a negative edge of a clock pulse.

These flip-flops are termed edge-triggered flip-flops. Positive edge triggering is

indicated schematically by a small angle bracket on the clock input to the flip-flop

(see Figure 6.8a ). Negative edge triggering is indicated schematically by a small

circle and angle bracket on the clock input (see Figure 6.8b ).

The function of the edge-triggered RS flip-flop is defined by the following rules:

1 . If S and R are both 0 when the clock edge is encountered, the output state

remains unchanged.

2 . If S is 1 and R is 0 when the clock edge is encountered, the flip-flop output is

set to 1. If the output is at 1 already, there is no change.

3 . If S is 0 and R is 1 when the clock edge is encountered, the flip-flop output is

reset to 0. If the output is at 0 already, there is no change.

4 . S and R should never both be 1 when the clock edge is encountered.

alc80237_ch06_197-257.indd 216alc80237_ch06_197-257.indd 216 11/01/11 3:54 PM11/01/11 3:54 PM

Confirming Pages

Figure 6.8 Edge-triggered RS flip-flops.

(a) positive edge-triggered (b) negative edge-triggered

Table 6.5 Positive edge-triggered RS flip-flop truth table

R CK Q

↑

0,1,↓

Figure 6.9 Positive edge-triggered RS flip-flop timing diagram.

6.9 Flip-Flops 217

The truth table for a positive edge-triggered RS flip-flop ( Figure 6.8a ) is given

in Table 6.5. The up-arrow ↑ in the clock (CK) column represents the positive edge

transition from 0 to 1. The NA in the second to last row indicates that the input con-

dition for that row is not allowed. As long as there is no positive edge transition, the

values of S and R have no effect on the output as shown by the X symbols in the last

row of the table. An example timing diagram is shown in Figure 6.9 . The output is

reset (Q  0) at the first positive edge of the clock signal, where R  1 and S  0,

and the output is set (Q  1) at the second positive edge, where S  1 and R  0.

There are special devices that are not edge triggered in the way just described.

An important example is called a latch. Its schematic symbol is shown in Figure 6.10 .

The output Q tracks the input D as long as CK is high. When a negative edge occurs

(i.e., when CK goes low), the flip-flop will store (latch) the value that D had at the

negative edge, and that value will be retained at the output. Because the output fol-

lows the input when the clock is high, we say the latch is transparent during this

alc80237_ch06_197-257.indd 217alc80237_ch06_197-257.indd 217 11/01/11 3:54 PM11/01/11 3:54 PM

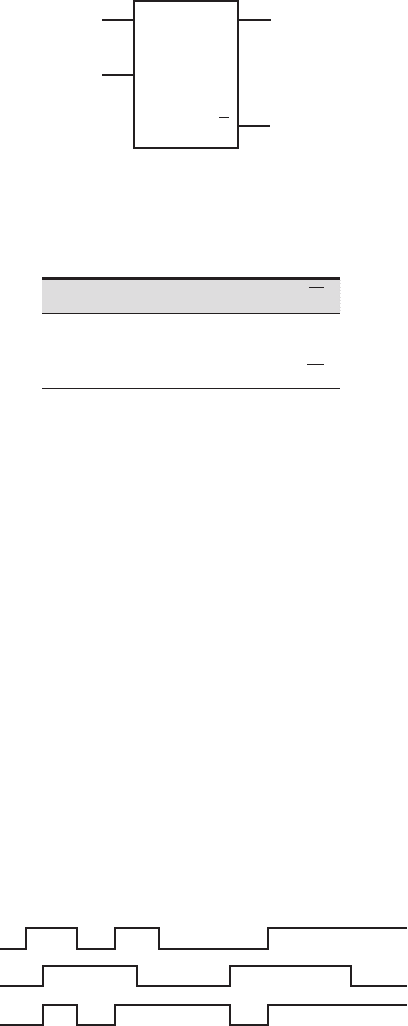
Confirming Pages

Table 6.6 Latch truth table

D CK Q Q

0101

011

Figure 6.10 Latch.

Figure 6.11 Latch timing diagram.

218 CHAPTER 6 Digital Circuits

time. The latch can also be referred to as a positive-level-triggered device. The truth

table for a latch is given in Table 6.6 , and a timing diagram example is shown in

Figure 6.11 . Note how the output (Q) tracks the input (D) while the clock level is

high (CK  1). The X in the last row of the table indicates that the value of D has no

effect on the output as long as CK is low.

6.9.2 Asynchronous Inputs

Flip-flops may have preset and clear functions that instantaneously override any

other inputs. They are called asynchronous inputs, because their effect may be

asserted at any time. They are not triggered by a clock signal. The preset input is

used to set or initialize the output Q of the flip-flop to high (1). The clear input is

used to clear or reset the output Q of the flip-flop to low (0). The small inversion

symbols shown at the asynchronous inputs in Figure 6.12 are typical of most devices

and imply that the function is asserted when the asynchronous input signal is low.

Such an input is referred to as an active low input. Both preset and clear should not

be asserted simultaneously. Either of these inputs can be used to define the state of a

flip-flop after power-up; otherwise, at power-up the output of a flip-flop is uncertain.

alc80237_ch06_197-257.indd 218alc80237_ch06_197-257.indd 218 11/01/11 3:54 PM11/01/11 3:54 PM

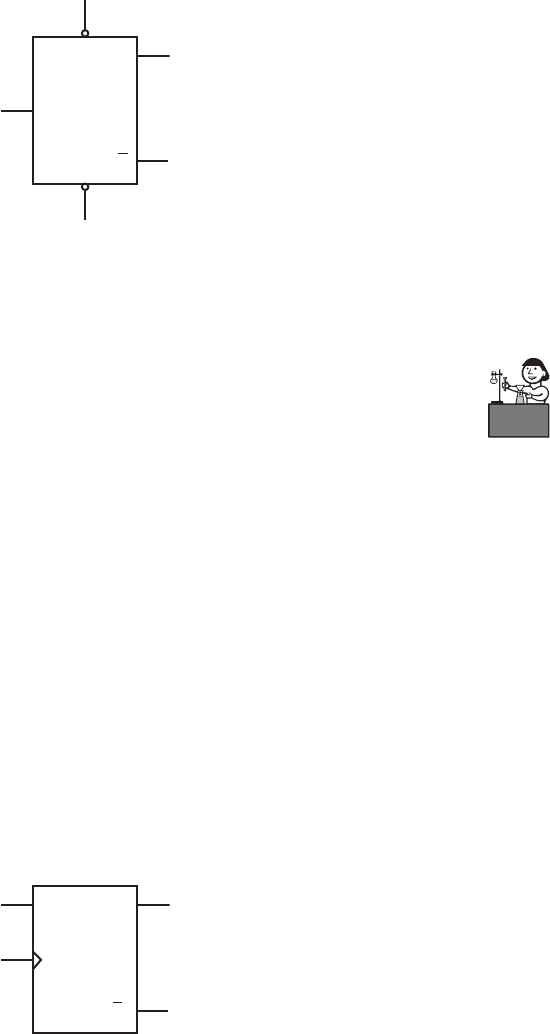
Confirming Pages

Figure 6.12 Preset and clear flip-flop functions.

Preset

Clear

Figure 6.13 Positive edge-triggered D flip-flop.

6.9 Flip-Flops 219

6.9.3 D Flip-Flop

The D flip-flop, also called a data flip-flop, has a single input D whose value is stored

and presented at the output Q at the edge of a clock pulse. A positive edge-triggered

D flip-flop is illustrated in Figure 6.13 , and its truth table is given in Table 6.7.

Unlike a latch, a D flip-flop does not exhibit transparency. The output changes only

when triggered by the appropriate clock edge (in this case, a positive edge).

Lab Exercise 7 explores latches and D flips-flops and shows how their functions

differ. The exercise also deals with logic gates and shows how to wire switches for

input into logic circuits.

6.9.4 JK Flip-Flop

The JK flip-flop is similar to the RS flip-flop where the J is analogous to the S (set)

input and the K is analogous to the R (reset) input. The major difference is that the

J and K inputs may both be high simultaneously. This state causes the output to

toggle, which means the output changes value (i.e., a 1 would become 0, and a 0

would become 1). The schematic representation and truth table for a negative edge-

triggered JK flip-flop are shown in Figure 6.14 and Table 6.8. The first two rows of

the table describe the preset or clear functions that can be used to initialize the output

of the flip-flop. Recall that these features are active low and override the other inputs.

The third row precludes presetting and clearing simultaneously. The symbol ↓

represents the negative edge of the clock signal, which causes the change in the

Lab Exercise

Lab 7Digital

circuits—logic

and latching

alc80237_ch06_197-257.indd 219alc80237_ch06_197-257.indd 219 11/01/11 3:54 PM11/01/11 3:54 PM

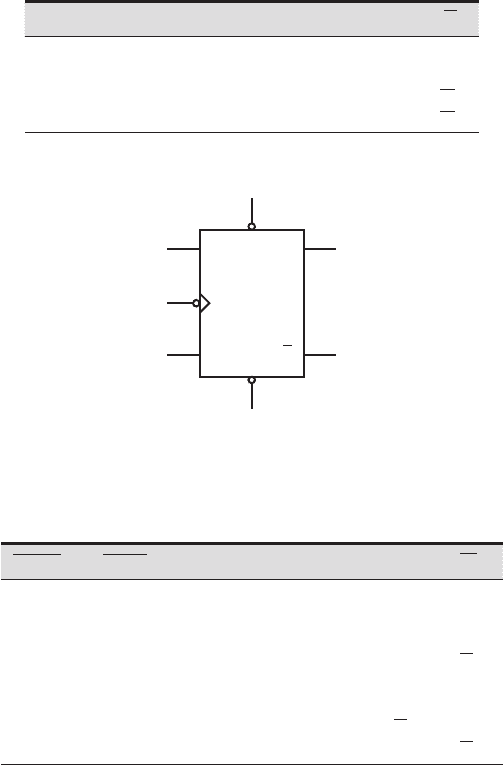
Confirming Pages

Table 6.7 Positive edge-triggered D flip-flop truth table

CK Q

↑

Figure 6.14 Negative edge-triggered JK flip-flop.

Preset

Clear

220 CHAPTER 6 Digital Circuits

Table 6.8 Truth table for a negative edge-triggered JK flip-flop

Preset Clear CK JK QQ

01XXX10

10XXX01

00 NA

11↓ 00

11↓ 10 10

11↓ 01 01

11↓ 11

1 1 0, 1 X X

output. The last row describes the memory feature of the flip-flop in the absence of

a negative edge.

The JK flip-flop has a wide range of applications, and all flip-flops can easily

be constructed from it with proper external wiring. The T (toggle) flip-flop serves

as a good example of this. The symbol for a positive edge-triggered T flip-flop and

the equivalent JK flip-flop implementation are shown in Figure 6.15 . The T flip-flop

simply toggles the output every time it is triggered. The preset and clear functions

are necessary to provide direct control over the output because the T input alone

provides no mechanism for initializing the output value. The truth table is given in

Table 6.9.

alc80237_ch06_197-257.indd 220alc80237_ch06_197-257.indd 220 11/01/11 3:54 PM11/01/11 3:54 PM