Alciatore D.G., Histand M.B. Introduction to Mechatronics and Measurement Systems

Подождите немного. Документ загружается.

Confirming Pages

5.14 The Real Op Amp 191

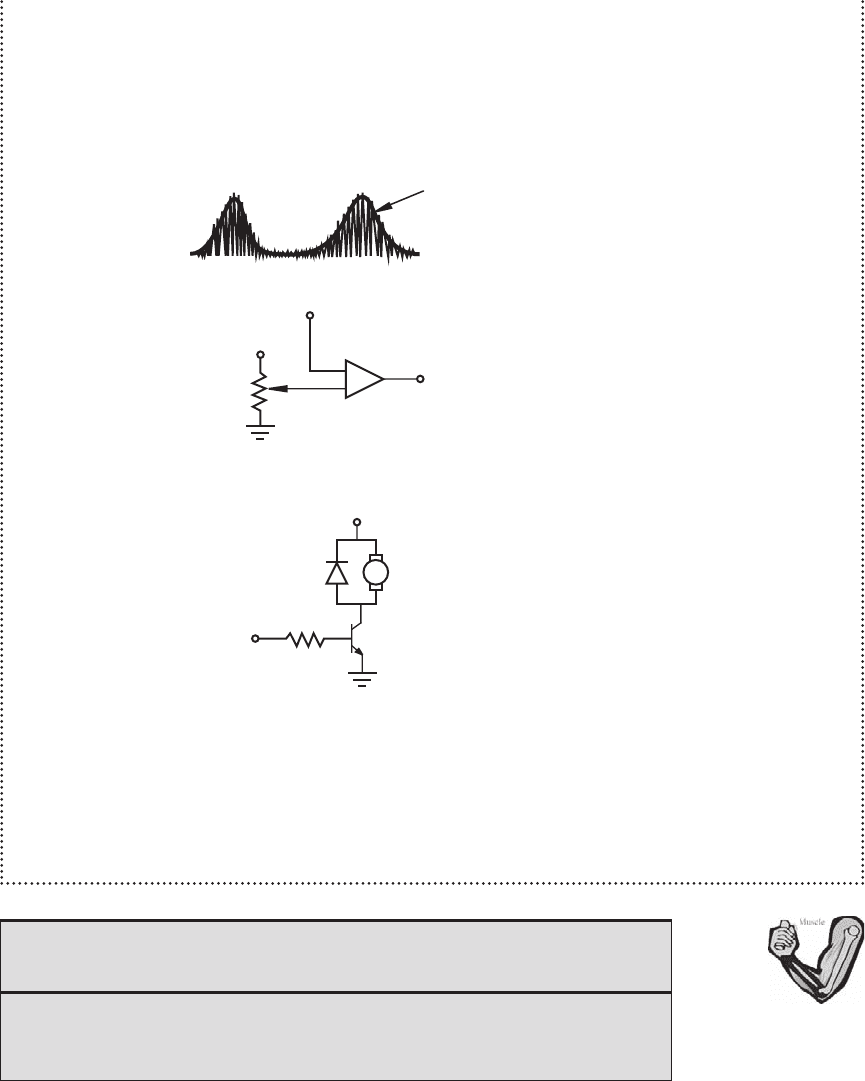
The precision-rectified EMG and the resulting low-pass-filtered signals look like those

shown in the next figure. The low-pass-filtered signal is basically the envelope of the recti-

fied signal. Now we have a signal that can be input to a comparator (see the figure that fol-

lows next) to provide a binary control signal (signal “D”), which will be on when the muscle

is contracted and off when relaxed. The designer or user can adjust the reference voltage

with the potentiometer for the desired sensitivity.

low-pass-filtered

signal

5 V

–

As shown in the final figure, the output of the rectifier can then be input to a power

transistor circuit to control the current in a motor.

supply

DC motor

In summary, we have used a variety of op amp circuits to process an analog signal. It

exemplifies the extraction of a very low level signal in the presence of noise, a variety of

analog signal processing methods, and the interface to an actuator to control mechanical

power. In this case, we have converted the EMG signal into a binary control signal for on-off

control of a DC motor that could, for example, flex the elbow in a prosthetic arm. A more

complete and detailed solution to a similar problem, where an EMG signal is used to control

an industrial robot, is presented in Section 11.4.

■ CLASS DISCUSSION ITEM 5.8

Bidirectional EMG Controller

In Design Example 5.1 , we discussed turning on and off a motor via an EMG sig-

nal. Unfortunately, the controller can actuate the joint in one direction only. Discuss

how you might change the design to allow bidirectional movement.

alc80237_ch05_161-196.indd 191alc80237_ch05_161-196.indd 191 1/3/11 4:10 PM1/3/11 4:10 PM

Confirming Pages

192 CHAPTER 5 Analog Signal Processing Using Operational Amplifiers

QUESTIONS AND EXERCISES

Section 5.5 Inverting Amplifier

5.1. An inverting op amp circuit is designed with 1/4 W resistors (i.e., they are capable of

dissipating up to 1/4 W of energy without failure). If the input voltage is 5 V, what

are the minimum required values for the input and feedback resistors if the gain is

a. 1

b . 1 0

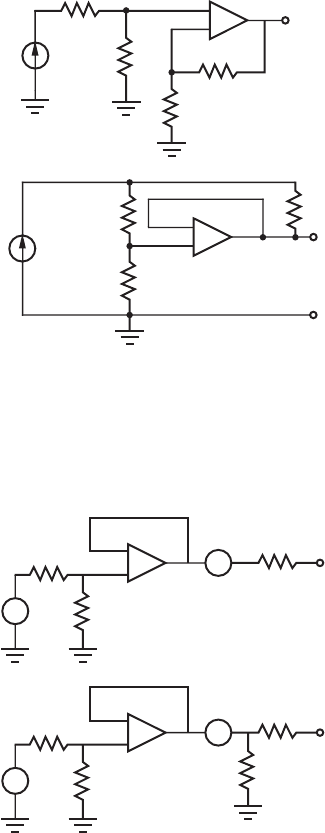
5.2. Determine V

out

as a function of I (provided by a current source) and the resistor

values for each of the op amp circuits that follows. Assume ideal op amp behavior.

(a)

out

–

(b)

–

Section 5.6 Noninverting Amplifier

5.3. If resistor R

shown in Figure 5.10 is replaced with a short (i.e., R

 0), what is the

gain of the circuit?

5.4. Determine V

out

in the following circuits with R

 R

 1 kΩ, V

 10 V, and

 5 V. Assume ideal op amp behavior.

(b)

–

(a)

out

–

alc80237_ch05_161-196.indd 192alc80237_ch05_161-196.indd 192 1/3/11 4:10 PM1/3/11 4:10 PM

Confirming Pages

Questions and Exercises 193

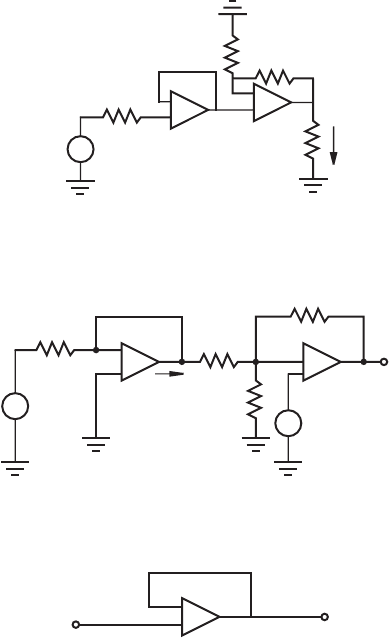
5.5. Determine I

in terms of V

, R

, and R

in the following circuit. Assume ideal

op amp behavior.

–

5.6. For the following circuit, express I

out

and V

out

in terms of V

, V

, and R.

out

–

5.7. Explain why V

out

 V

in the following circuit.

out

–

Section 5.7 Summer

5.8. Analyze the summer circuit in Figure 5.13 and determine an equation for the out-

put voltage V

out

in terms of the input voltages V

and V

and the resistances R

, R

and R

. Use this result to verify that Equation 5.19 is correct. Show and explain all

work.

5.9. If a voltage source V

is inserted between ground and the noninverting input in the

summer circuit shown in Figure 5.13 , what is the resulting equation for the output

voltage V

out

in terms of the input voltages V

and V

if R

 R

Section 5.8 Difference Amplifier

5.10. Derive Equation 5.24 for the difference amplifier without using the principle of

superposition.

alc80237_ch05_161-196.indd 193alc80237_ch05_161-196.indd 193 1/3/11 4:10 PM1/3/11 4:10 PM

Confirming Pages

194 CHAPTER 5 Analog Signal Processing Using Operational Amplifiers

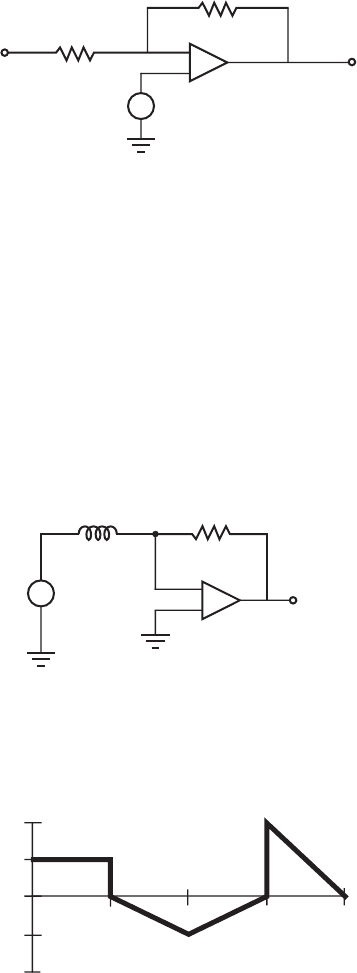
5.11. Use the principle of superposition to derive an expression for the output voltage in

the following circuit and explain why the circuit is called a level shifter.

ref

–

Section 5.9 Instrumentation Amplifier

5.12. Derive Equation 5.31 that expresses V

out

in terms of the V

and V

shown in

Figure 5.17 .

Section 5.10 Integrator

5.13. Solve and generate plots for Class Discussion Item 5.4 for a 100 Hz sine wave with

an amplitude of 1 V and a DC offset of 0.1 V. Plot the output for 5 cycles of the

sinusoid.

Section 5.11 Differentiator

5.14. Find V

out

( t ) given V

( t ) in the op amp circuit that follows.

out

(t)

–

5.15. Derive Equation 5.36 assuming the input and output voltages are both zero and the

currents flowing into each op amp input are equal.

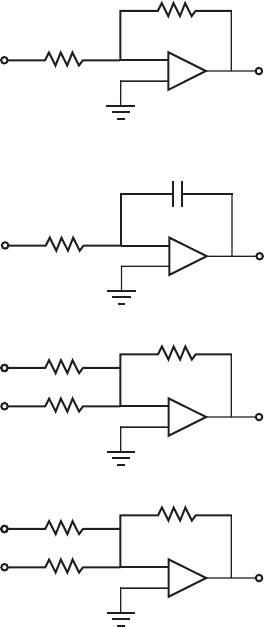
5.16. Using the following input waveform, sketch the corresponding output waveform for

each op amp circuit (a through d). Assume ideal op amp behavior.

–1

–2

volts

, V

sec

alc80237_ch05_161-196.indd 194alc80237_ch05_161-196.indd 194 1/3/11 4:10 PM1/3/11 4:10 PM

Confirming Pages

Questions and Exercises 195

(a)

50 kΩ

out

25 kΩ

–

(c)

5 kΩ

out

5 kΩ

10 kΩ

–

(d)

5 kΩ

out

5 kΩ

10 kΩ

–

(b)

100 kΩ

–

10 μF

Section 5.13 Comparator

5.17. Using a standard output (not open-collector) comparator, draw a circuit that could be

used to turn on an LED when an input voltage exceeds 5 V.

5.18. Using an open-collector output comparator, draw a circuit that could be used to turn

on an LED when an input voltage exceeds 5 V.

Section 5.14 The Real Op Amp

5.19. If the short-circuit output current of a real op amp is 10 mA, calculate the minimum

resistance required for the feedback resistor in an inverting op amp circuit with a gain

of 10 and a maximum output voltage of 10 V.

alc80237_ch05_161-196.indd 195alc80237_ch05_161-196.indd 195 1/3/11 4:10 PM1/3/11 4:10 PM

Confirming Pages

196 CHAPTER 5 Analog Signal Processing Using Operational Amplifiers

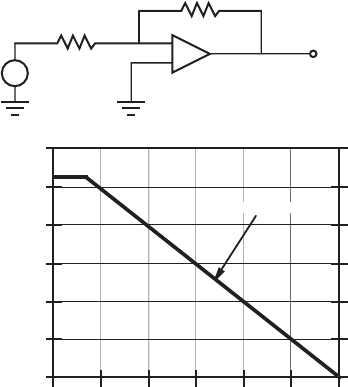
5.20. Given the following circuit and op amp open loop gain curve, what is the fall-off

frequency for the circuit when R

 20 kΩ and R  2 kΩ?

100

1000

100

120

frequenc

(Hz)

gain

1 10 100 1000

out

–

open loop gain

5.21. Document a complete and thorough answer to Class Discussion Item 5.7.

BIBLIOGRAPHY

Coughlin, R. and Driscoll, F., Operational Amplifiers and Linear Integrated Circuits,

4th Edition, Prentice-Hall, Englewood Cliffs, NJ, 1991.

Horowitz, P. and Hill, W., The Art of Electronics, 2nd Edition, Cambridge University Press,

New York, 1989.

Johnson, D., Hilburn, J., and Johnson, J., Basic Electric Circuit Analysis, 2nd Edition,

Prentice-Hall, Englewood Cliffs, NJ, 1984.

McWhorter, G. and Evans, A., Basic Electronics, Master Publishing, Richardson, TX, 1994.

Mims, F., Engineer’s Mini-Notebook: Op Amp IC Circuits, Radio Shack Archer Catalog

No. 276-5011, 1985.

Mims, F., Getting Started in Electronics, Radio Shack Archer Catalog No. 276-5003A, 1991.

Texas Instruments, Linear Circuits Data Book, Volume 1—Operational Amplifiers, Dallas,

TX, 1992.

alc80237_ch05_161-196.indd 196alc80237_ch05_161-196.indd 196 1/3/11 4:10 PM1/3/11 4:10 PM

Confirming Pages

197

CHAPTER

Digital Circuits

his chapter presents digital electronic devices used for logic, display,

sequencing, timing, and other functions in mechatronic systems. The fun-

damentals presented in this chapter are important in understanding the basic

functioning of all digital components and systems used in the control of mechatronic

systems. ■

INPUT SIGNAL

CONDITIONING

AND INTERFACING

discrete circuits

- amplifiers

- filters

- A/D, D/D

OUTPUT SIGNAL

CONDITIONING

AND INTERFACING

- D/A, D/D

- PWM

- power transistors

- power op amps

GRAPHICAL

DISPLAYS

- LEDs

digital displays

- LCD

- CRT

SENSORS

- switches

- potentiometer

- photoelectrics

- digital encoder

- strain gage

- thermocouple

- accelerometer

- MEMs

ACTUATORS

- solenoids, voice coils

- DC motors

- stepper motors

- servo motors

- hydraulics, pneumatics

MECHANICAL SYSTEM

- system model - dynamic response

DIGITAL CONTROL

ARCHITECTURES

logic circuits

- microcontroller

- SBC

- PLC

sequencing and timing

logic and arithmetic

- control algorithms

- communication

- amplifiers

CHAPTER OBJECTIVES

After you read, discuss, study, and apply ideas in this chapter, you will:

1. Be able to define a digital signal

2. Understand how the binary and hexadecimal number systems are used in

coding digital data

3. Know the characteristics of different logic gates

4. Know the differences between combinational and sequential logic

alc80237_ch06_197-257.indd 197alc80237_ch06_197-257.indd 197 11/01/11 3:53 PM11/01/11 3:53 PM

Confirming Pages

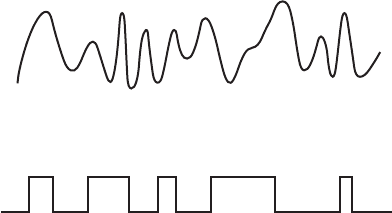
Figure 6.1 Analog and digital signals.

analog signal

digital signal

198 CHAPTER 6 Digital Circuits

5. Be able to draw a timing diagram for a digital circuit

6. Be able to use Boolean mathematics to analyze logic circuits

7. Be able to design logic networks

8. Be able to use a variety of flip-flops for storing data

9. Understand differences between TTL and CMOS logic devices

10. Know how to construct an interface between TTL and CMOS devices

11. Be able to use counters for different counting applications

12. Know how to display numerical data using LED displays

6.1 INTRODUCTION

In contrast to an analog signal that changes in a continuous manner, a digital signal

exists only at specific levels or states and changes its level in discrete steps. An ana-

log signal and a digital signal are illustrated in Figure 6.1 . Most digital signals have

only two states: high and low. A system using two-state signals allows the applica-

tion of Boolean logic and binary number representations, which form the foundation

for the design of all digital devices.

Digital devices are categorized according to their function as combinational

logic or sequential logic devices. Digital devices convert digital inputs into one or

more digital outputs. The difference between the two categories is based on signal

timing. For sequential logic devices, the timing, or sequencing history, of the input

signals plays a role in determining the output. This is not the case with combinational

logic devices whose outputs depend only on the instantaneous values of the inputs.

Before we introduce the various digital devices, we will review the binary num-

ber system and the application of binary numbers in digital calculations. Then we

discuss Boolean algebra, which is the mathematical basis for digital computations.

Finally, we discuss a number of specific combinational and sequential logic devices

and their applications.

alc80237_ch06_197-257.indd 198alc80237_ch06_197-257.indd 198 11/01/11 3:53 PM11/01/11 3:53 PM

Confirming Pages

6.2 Digital Representations 199

6.2 DIGITAL REPRESENTATIONS

We grow up becoming proficient using the base 10 decimal number system. The

base of the number system indicates the number of different symbols that can

be used to represent a digit. In base 10, the symbols are 0, 1, 2, 3, 4, 5, 6, 7, 8,

and 9. Each digit in a decimal number is a placeholder for different powers of 10

according to

n 1–

. . .

n 1–

⋅

. . .

⋅ d++

⋅ d

⋅+=

(6.1)

where n is the number of digits and each digit d

is one of the ten symbols. Note that

the highest power of 10 is ( n  1), 1 less than the number of digits. As an example,

the decimal number 123 can be expanded as

123 = 1 × 10

+ 2 × 10

+ 3 × 10

(6.2)

Fractions may also be included if digits for negative powers of 10 are included

( d

 1

, d

 2

, . . .).

In order to represent and manipulate numbers with digital devices such as com-

puters, we use a base 2 number system called the binary number system. The rea-

son for this is that the operation of digital devices is based on transistors that switch

between two states: the ON or saturated state and the OFF or cutoff state. These

states are designated by the symbols 1 (ON) and 0 (OFF) in the base 2 system. The

digits in a binary number, as with the base 10 system, correspond to different powers

of the base. A binary number can be expanded as

n 1–

. . .

)

n 1–

·2

n 1–

. . .

·2

d++

·2

(6.3)

where each digit d

is one of the two symbols 0 and 1. The trailing subscript 2 is used

to indicate that the number is base 2 and not the normally assumed base 10. As an

example of Equation 6.3 , the binary number 1101 can be expanded as

1101

⋅+⋅ 02

⋅ 12

⋅++ 8

++ 13

===

(6.4)

The digits of a binary number are also called bits, and the first and last bits have

special names. The first, or leftmost, bit is known as the most significant bit (MSB)

because it represents the largest power of 2. The last, or rightmost, bit is known

as the least significant bit (LSB) because it represents the smallest power of 2.

A group of 8 bits is called a byte.

In general, the value of a number represented in any base can be expanded and

computed with

n 1–

. . .

()

n 1–

⋅

. . .

⋅ d

⋅+⋅++()=

(6.5)

where b is the base and n is the number of digits. Often it is necessary to convert from

one base system to another. Equation 6.5 provides a mechanism to convert from an

arbitrary base to base 10. To convert a number from base 10 to some other base, the

procedure is to successively divide the decimal number by the base and record the

alc80237_ch06_197-257.indd 199alc80237_ch06_197-257.indd 199 11/01/11 3:53 PM11/01/11 3:53 PM

Confirming Pages

200 CHAPTER 6 Digital Circuits

Table 6.1 Decimal to binary conversion

Successive Divisions Remainder

123/2 1 LSB

61/2 1

30/2 0

15/2 1

7/2 1

3/2 1

1/2 1 MSB

Result 1111011

remainders after each division. The remainders, when written in reverse order from

left to right, form the digits of the number represented in the new base. Table 6.1

illustrates this procedure by converting the decimal number 123 to its binary equiva-

lent. You can use Equation 6.3 to verify the binary result by calculating its expansion.

Binary arithmetic is carried out in the same way as the more familiar base 10

arithmetic. Example 6.1 illustrates the similarities. Video Demo 6.1 shows a binary

counting machine using marbles as bits and wood toggle switches to store values. It

quite nicely illustrates how binary counting and bit-carry work.

Video Demo

6.1Binary

counting machine

using marbles

and wood toggle

switches

This example illustrates the analogy between decimal addition and multiplication and binary

addition and multiplication. Note that, when adding two 1 bits (1  1), the sum is 0 with a

carry of 1 to the next higher order bit. This occurs in the addition example below, where a 1

is carried from bit one to bit two and from bit two to bit three:

1 1

9 1001 9 1001

 3  0011  3  0011

12 1100 27 1001

 1001

 0000

11011

Binary Arithmetic

EXAMPLE 6.1

Because binary numbers can be long and cumbersome to write and display,

often the hexadecimal (base 16) number system is used as an alternative representa-

tion. Table 6.2 lists the symbols for the hexadecimal system along with their binary

and decimal equivalents. Note that the letters A through F are used to represent the

digits larger than 9.

To convert a binary number to hexadecimal, divide the number into groups of

four digits beginning with the least significant bit and replace each group with its

hexadecimal equivalent. For example,

123

0111 1011

(6.6)

alc80237_ch06_197-257.indd 200alc80237_ch06_197-257.indd 200 11/01/11 3:53 PM11/01/11 3:53 PM