9-й Международный симпозиум по электромагнитной совместимости и электромагнитной экологии
Подождите немного. Документ загружается.


381
ELECTROMAGNETIC FIELD STUCTURE ANALYSIS IN THE PRESENCE
OF RADIO ABSORBING COATED COVER
M. Yu. Z
VEZDINA
1
, R
USSIA
, Yu. A. Z
VEZDINA
1
, R
USSIA
, S. N. Z
ABELKIN
1
, R
USSIA
,
A.
V.
P
ODZOROV
2
, R
USSIA
, A. N. S
AMODELOV
3
, R
USSIA
1
Rostov Technology Institute of Service and turism of South Russian State University of Economy and Service,
e-mail: zvezdina_m@mail.ru,
2
Rostov Military Institute of Missile Corps,
3
South Russian State University of Economy
and Service, e-mail:
samodelov@gmail.com
One of the ways for increasing the electromagnetic
compatibility of the radioelectronic devices is the appli-
cation of the radio absorbing coatings. The coatings are
designed multilayer to work in the broadband, the meta-
materials with magnetodielectric properties are used to
improve their absorption. The variety of the metamate-
rial design specifies using the closed form solutions of
the electromagnetic wave diffraction problem for the
metallic coated body. The closed form allows carrying
out the full-waveform analysis of the excited electro-
magnetic field structure.
In spite of their canonical form, the well-known so-
lutions of the diffraction problem do not consider the
case of metallic circular cylinder of resonant size with
multilayer magnetodielectric coating. Thus the bordering
method with an account of diagonal matrix of unknown
spectral coefficients of field expanding is proposed to
solve the problem in a closed form
The bordering method modification allows writing
down the analytic correlations that describe the inverse
matrix. The computational costs estimation for finding
the field expansion coefficients shows that when using
the solution obtained with the bordering method it is not
necessary to store the initial
1
4
−
M
х
1
4
−
M
matrix if
its band structure is taken into an account. The obtained
correlations can be used to find the unknown coefficients
directly. The obtained solution independence of the ex-
ternal source disposition towards the coating layers, the
explicit form of the inverse matrix and thus the substan-
tial decrease of the computational costs are the advan-
tages of the proposed solution. Non-uniqueness of the
inverse matrix in passing from the block matrix repre-
sentation to element representation is its disadvantage.
One of the possible ways to overcome it is to decompose
the initial matrix into square blocks of a smaller dimen-
sion (not
4
4
×
, but
2
2
×
).
The scattered electromagnetic field structure analy-
sis was carried out in the far region using the proposed
scientific technique. It is shown that the application of a
two-layer coating made of composite metamaterials with
metallic inclusion gives more opportunities to manage
the scattered electromagnetic field structure comparing
to a single layer coating. The recommendations are given
for choosing the coating refraction index distribution in
vertical direction to provide the minimum level of scat-
tered field. Thus, the minimum level of the field scat-
tered by a cylinder in the forward direction for E-
polarized incident wave can be achieved by choosing the
two-layer coating parameters in a way that guarantees
the total reflection on the bottom boundary of the coating
at lower incident angle.
Backlobe level can be reduced by 5..7 dB for H-
polarized wave and by 2..3 dB for E-polarized wave by
using the two-layer coating comparing to a single layer
coating. Moreover, the directional pattern beamwidth
narrows by 7 degrees in average comparing to the un-
coated cylinder.
382
МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ В ЗАДАЧАХ РАСЧЕТНОГО
ПРОГНОЗИРОВАНИЯ БЛИЖНЕГО ЭЛЕКТРОМАГНИТНОГО ПОЛЯ
ЗЕРКАЛЬНЫХ АНТЕНН
Е.
А.
А
ЛАШЕЕВА
,
Р
ОССИЯ
,
М.
Ю.
М
АСЛОВ
,
Р
ОССИЯ
,
Д.
В.
С
КАЧКОВ
,
Р
ОССИЯ
Поволжский государственный университет телекоммуникаций и информатики, e-mail: mike@psati.ru
Аннотация. В задачах расчетного прогнозирования ближнего электромагнитного поля зеркальных
антенн наряду с традиционным апертурным методом в последние годы активно развиваются подхо-
ды, основанные на интегрировании истинных функций распределения токов на поверхности зеркала.
При этом токи определяются методами теории дифракции. В докладе проанализированы способы
решения, нашедшие широкое применение для решения рассматриваемого класса задач. Особое вни-
мание уделено проблеме выбора базиса разложения токовой функции. Приводятся результаты чис-
ленного моделирования ближних полей антенн с различной конфигурацией зеркала.
Abstract. In problems of settlement forecasting of near electromagnetic field of reflector antennas along
with a traditional aperture method last years the approaches based on integration of true functions of current
distribution on a reflector surface actively develop. Thus currents are defined by methods of the diffraction
theory. In the report the modes of solution, found wide application for the decision of a considered class of
problems are analyzed. The special attention is given to a choice of basis functions for decomposition the
current distribution. Results of numerical modeling of near antenna fields for various configurations of mir-
rors are resulted.
Введение
При решении ряда прикладных задач электроди-
намики и теории антенн часто возникает проблема ана-
лиза электромагнитного поля, рассеянного проводя-
щими телами, расположенными в непосредственной
близости от излучающей системы. К подобным задачам
относятся расчет ближних полей апертурных антенн, а
также учет влияния подстилающей поверхности и
иных материальных тел, расположенных вблизи антен-
ны, таких как затеняющие металлоконструкции, импе-
дансные структуры и т.п. При этом в ряде случаев рас-
сеивающие тела могут быть представлены тонкими
проводящими поверхностями ограниченных размеров.
В связи с имеющим место в последние десятиле-
тия активным развитием методов вычислительной
математики, применяемых для решения задач об из-
лучении, возникло множество методик решения ин-
тегральных уравнений, имеющих смысл тех или иных
граничных условий, наиболее распространенными из
которых являются различные модификации метода
моментов [1, 4].
Однако, упомянутые выше методики встречают-
ся в литературе в основном для решения задач ди-
фракции, сводимых к одномерным интегральным
уравнениям [2]. Практически нигде не встречаются
оценки эффективности существующих алгоритмов и
четкие методики решения задач дифракции, сводимых
к двумерным интегральным уравнениям.
Вывод исходных уравнений
Сведение задачи дифракции к системе двумер-
ных интегральных уравнений Фредгольма подразуме-
вает более общее решение поставленной задачи, так
как появляется возможность отказаться от специаль-
ных систем координат. Кроме того, отпадает необхо-
димость выбора среди всех возможных решений диф-
ференциального уравнения частного решения, удов-
летворяющее данной задаче. В данном случае прямо
получается единственное решение, за исключением
тех редких случаев, когда уравнение имеет бесконеч-
но много решений или вовсе не имеет решения.
Еще одним толчком для исследования двумерных
задач дифракции послужил ряд открытий в области
вычислительной математики. Например, вейвлет-
функции появились сравнительно недавно, в середине
80-х годов, и завоевали популярность в связи с рядом
преимуществ перед классическими ортогональными
системами базисных функций, включая тригономет-
рические полиномы, ряды Фурье, алгебраические по-
линомы, для широкого круга задач. Это обстоятельст-
во делает перспективным применение wavelet-систем
для численного решения многомерных интегральных
уравнений. Методы работы с псевдоразреженными
матрицами широко представлены в [3].
В докладе приводятся результаты разработки ма-
тематических моделей двумерных идеально проводя-
щих излучающих структур на основе аппарата дву-
мерных интегральных уравнений. Разработан новый
эффективный алгоритм решения двумерных инте-
гральных уравнений, к которым сводятся внутренние
электродинамические задачи для следующих излу-
чающих структур:
– идеально проводящий плоский экран;
– зеркало в форме параболического цилиндра;
– зеркало в форме параболоида вращения,
возбуждаемых элементарным электрическим излуча-
телем (ЭЭИ) и элементарным магнитным излучателем
(ЭМИ).
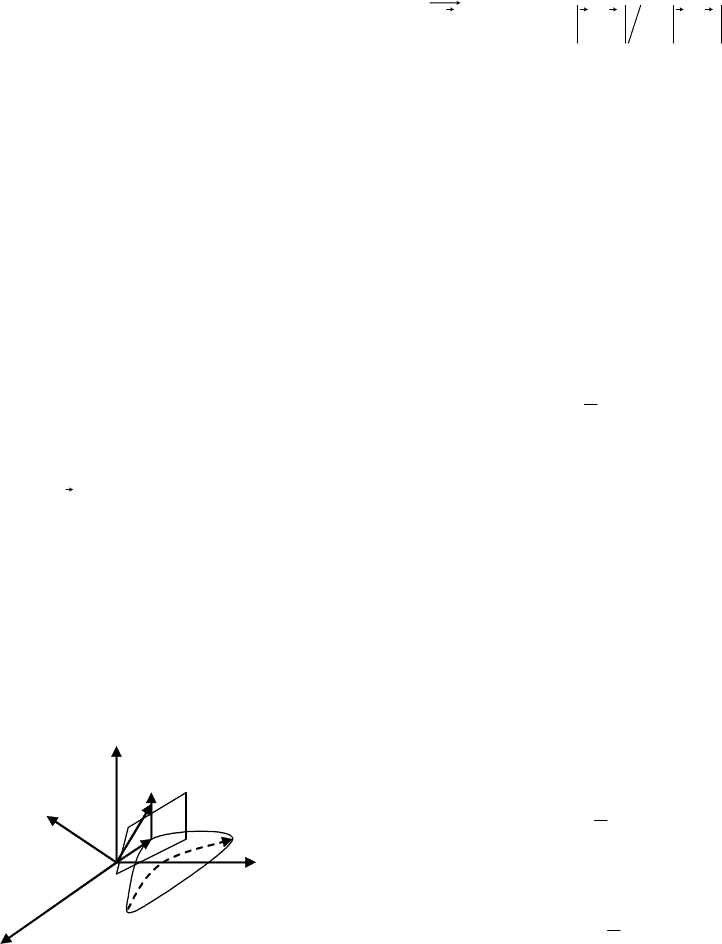
383
Разработка численных методов решения задач
дифракции открыла широкие возможности для анали-
за влияния поверхностей произвольной конфигурации
на структуру электромагнитного поля. При этом воз-
никла проблема создания общих вычислительных
алгоритмов, позволяющих исследовать широкий
класс задач. Методы, разработанные на основе при-
менения различного математического аппарата, жест-
ко связаны с определенными классами незамкнутых
поверхностей и неприменимы для поверхностей про-
извольной формы. В этом отношении универсальным
математическим аппаратом являются интегро-
дифференциальные уравнения, которые позволяют
подойти с единых позиций к анализу дифракции ра-
диоволн на поверхностях произвольной формы.
Рассмотрим общий принцип построения инте-
гральных уравнений для электродинамических задач,
который затем применяется для моделирования иссле-
дуемых задач. Особенность данной модели заключает-
ся в том, что задача рассеяния электромагнитного поля
тонким телом исследована не как краевая задача для
неоднородного уравнения Гельмгольца, а как система
интегральных (интегро-дифференциальных) уравнений
(ИУ), относительно поверхностной плотности тока или
тангенциальных компонент суммарных электрического
или магнитного полей. Система ИУ может быть полу-
чена из интегральных соотношений для векторного или
скалярного потенциалов вторичного поля [2].
Пусть элементарный излучатель находится в точ-
ке с координатами
},,{
'''
'
zyxr =
(рис. 1) вблизи про-
водящего тела. Амплитуда тока, возбуждающего из-
лучатель I, длина излучателя l. Здесь и далее штрихо-
ванные координаты обозначают точки источников
первичного поля. Геометрические параметры задачи
очевидны из рис. 1.
},,{ zyxr
=
-
радиус
–
вектор
точки
наблюдения
,
{
}
zyxr
′
′
′
=
′
,,
-
радиус
–
вектор
точки
источника
,
{
}
zyxr
′
′
′
′
′
′
=
′
′
,,
-
радиус
–
вектор
точки
на
по
-
верхности
экрана
.
x
y
z
r
′
r
r
r
r
r
′′
n
r
S
Рис
. 1.
К
выводу
интегральных
уравнений
.
П
p
и
выводе
ИУ
воспользуемся
граничным
усло
-
вием
для
магнитного
поля
на
поверхности
проводя
-
щего
тела
в
следующей
форме
:
0
0
=−
S
НН
ττ
r
r
, (1)
где
0
τ
H
r
и
S
H
τ
r
,
соответственно
,
тангенциальные
компоненты
вектора
напряженности
первичного
маг
-
нитного
поля
и
поля
рассеяния
на
поверхности
S.
Для
тангенциальной
компоненты
магнитного
по
-
ля
рассеяния
справедливо
выражение
:
(
)
(
)
(
)
dSrr
S
Gr
S
jr
S
Н ],[grad
′′′
∫
×
′′
=
r
r
r
r
r
r
τ
, (2)
где
(
)
r
S
j
′′
r
r
-
вектор
плотности
тока
на
поверхности
S
,
n
r
-
вектор
нормали
в
точке
с
координатами
r
′
′
r
,
)"4("exp()",( rrrrkirrG −−⋅⋅−=
π
-
функция
Грина
для
свободного
пространства
,
λ
π
/2
=
k
-
вол
-
новое
число
.
Штрих
у
оператора
grad
в
(2)
указывает
на
то
,
что
дифференцирование
производится
по
коор
-
динатам
r
′
′
r
.
Выражение
(2)
с
учетом
граничного
условия
(1)
можно
представить
в
виде
:
(
)
(
)
(
)
( ) ( )
,],[gradlim
0
0000
∫
⋅
′′′
×
′′
×
×=×
→
S
S
rr
dSrrGrj
rnrНrn
rrr
r
r
r
r
r
r
r
rr
(3)
где
0
r
r
–
текущая
координата
на
поверхности
S.
Вычисление
предела
в
(3) c
помощью
теории
потен
-
циалов
приводит
к
следующему
интегральному
урав
-
нению
[5]:
( ) ( ) ( ) ( )
( ) ( )
[ ]
{
}
. ,grad
2
1
0
00000
dSrrGrj
rnrjrНrn
S
S
S
′
′′
×
′′
×
×−=×
∫
rrr
r
rrr
r
r
r
rr
(4)
Векторное
уравнение
(4)
можно
представить
в
виде
совокупности
двух
скалярных
уравнений
сле
-
дующим
образом
[5, 6].
Введем
два
ортогональных
базисных
вектора
в
плоскости
,
касательной
поверх
-
ности
S,
таким
образом
,
что
(
)
(
)
(
)
00201
rnrr
r
r
r
r
r
r
=×
ττ
. (5)
Очевидно
,
что
введенные
орты
соотносятся
меж
-
ду
собой
следующим
образом
:
(
)
(
)
(
)
( ) ( ) ( )
01002
02001
rrnr
rrnr
rrrrrr
r
r
r
r
r
r
ττ
ττ
=×
−=×
, (6)
Тогда
(4)
распадается
на
два
уравнения
относи
-
тельно
двух
ортогональных
компонент
вектора
плот
-
ности
тока
:
( ) ( ) ( ) ( )
( ) ( ) ( )
[ ]
{ }
,,grad
2
1
002
0010002
dSrrGrjr
rjrrНr
S
S
S
′
′′
×
′′
⋅−
−⋅−=⋅
∫
rrr
r
rr
r
r
rrr
r
rr
τ
ττ
(7)
( ) ( ) ( ) ( )
( ) ( ) ( )
[ ]
{ }
. ,grad
2
1
001
0020001
dSrrGrjr
rjrrНr
S
S
S
′
′′
×
′′
⋅+
+⋅−=⋅−
∫
rrr
r
rr
r
r
rrr
r
rr
τ
ττ
(8)
В
зависимости
от
вида
элементарного
излучате
-
ля
,
вертикального
ЭЭИ
,
горизонтального
ЭЭИ
,
верти
-
кального
ЭМИ
,
горизонтального
ЭМИ
,
левые
части
уравнений
будут
иметь
различный
вид
[5, 6].
384
Численное решение
Решение электродинамической задачи можно
разделить на три этапа:
- получение математических соотношений между
интересующими нас физическими величинами;
- введение определенных ограничений на пове-
дение полей и источников на соответствующих по-
верхностях;
- получение численных результатов.
Для решения поставленной задачи будем исполь-
зовать метод моментов, сравним следующие его виды:
метод Галеркина (Бубнова – Галеркина) [4], метод
наименьших квадратов, метод разделения области:
- метод Галеркина удобен тем, что базисные
функции совпадают с весовыми;
- метод наименьших квадратов удобен тем, что
матрица системы, получаемой при дискретизации
уравнения симметрична, однако существуют ограни-
чения в его применении, например, в случае вибрато-
ра с плоскими торцами имеется известная особен-
ность на ребре, наличие этой особенности приводит к
ошибкам в определении величины рассеянного поля
вблизи торцов;
- метод разделения области удобен тем, что при
выборе весовых функций в виде дельта – функций
все интегрирование сводится лишь к вычислению ин-
тегрального оператора.
При дискретизации уравнения в процессе решения
его методом моментов часто возникают СЛАУ доволь-
но высоких порядков, решение которых занимает дли-
тельное время. Поэтому приведём описание прибли-
женных методов: метод разряжённой матрицы и итера-
ционные методы. В рамках представления данных ме-
тодов разработан оригинальный алгоритм с использо-
ванием открытых недавно вейвлет – функций, который
приводит к применению разряжённых технологий. Это
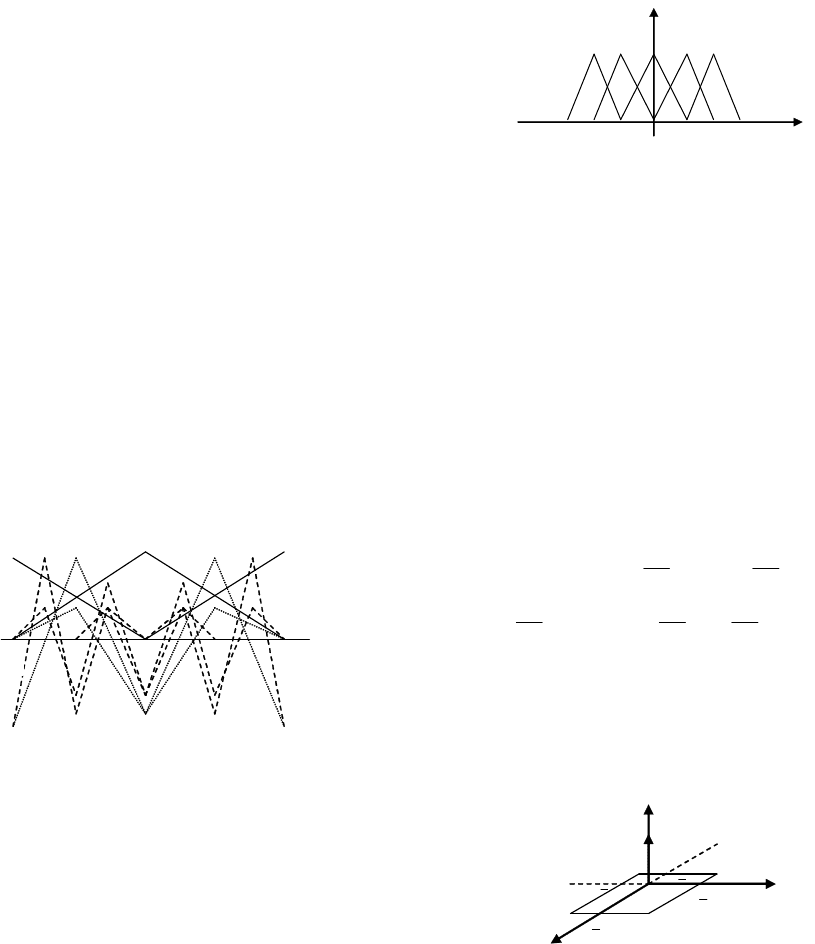
возможно из-за особенностей вейвлет – базиса (рис. 2),
так как одни его элементы малы по абсолютной вели-
чине по сравнению с другими.
а
с
Рис.2. Базис, составленный из линейных сплай-
нов, обыкновенных и граничных вейвлет.
Известно, что существует два вида систем базис-
ных функций: базисы полной области (базисные
функции определены на всей области определения
интегрального оператора) и базисы подобластей (ба-
зисные функции финитные). Системы базисных
функций полной области наиболее эффективно ис-
пользовать в случае предполагаемого гладкого реше-
ния электродинамической задачи, а базисы подобла-
стей, напротив, лучше использовать в случае получе-
ния предполагаемого негладкого решения. В [6] выде-
лены особенности решения двумерной задачи: здесь
пространство рассматривается как тензорное произве-
дение подпространств (9), что существенно увеличи-
вает порядок получаемой СЛАУ.
yx
LLL ×= (9)
Существует множество примеров базисных
функций подобластей и полной области. Например,
поставленную задачу можно решать с использованием
в качестве базиса сплайновых функций.
)()(),(
1,
yxyxJ
j
m
ji
iij
ϕϕα
∑
=
=
, (10)
где )(),( yx
ji
ϕϕ
- сплайны степени m-1 дефекта 1
(линейные сплайны) (рис. 3):
x
y
-a/2 a/2
Рис. 3. Линейные сплайны.
Решение поставленной задачи ищется методом
Галеркина – совпадение базисных функций с весовыми
существенно упрощает алгоритм решения. В качестве
базисных функций наиболее рационально использовать
разложение искомой функции в двумерный ряд Фурье.
При таком выборе базис по форме близок к ожидаемо-
му результату, что значительно снижает порядок мат-
рицы импедансов, получаемой при дискретизации ин-
тегрального уравнения. Кроме того, в данном случае
область определения интегрального оператора доволь-
но проста, поэтому можно выбрать базис полной об-
ласти. Применение двумерного ряда Фурье вместо
вейвлет – базиса и сплайнового базиса значительно
сокращает время вычисления.
Решение поставленной задачи ищется в виде:
...,
2
cos
2
coscos
2
2
sin
2
cos),(
54
321
+++
+++=
yxaya
xaxaayxJ
λ
π
λ
π
λ
π
λ
π
λ
π
(11)
где
λ
– длина волны.
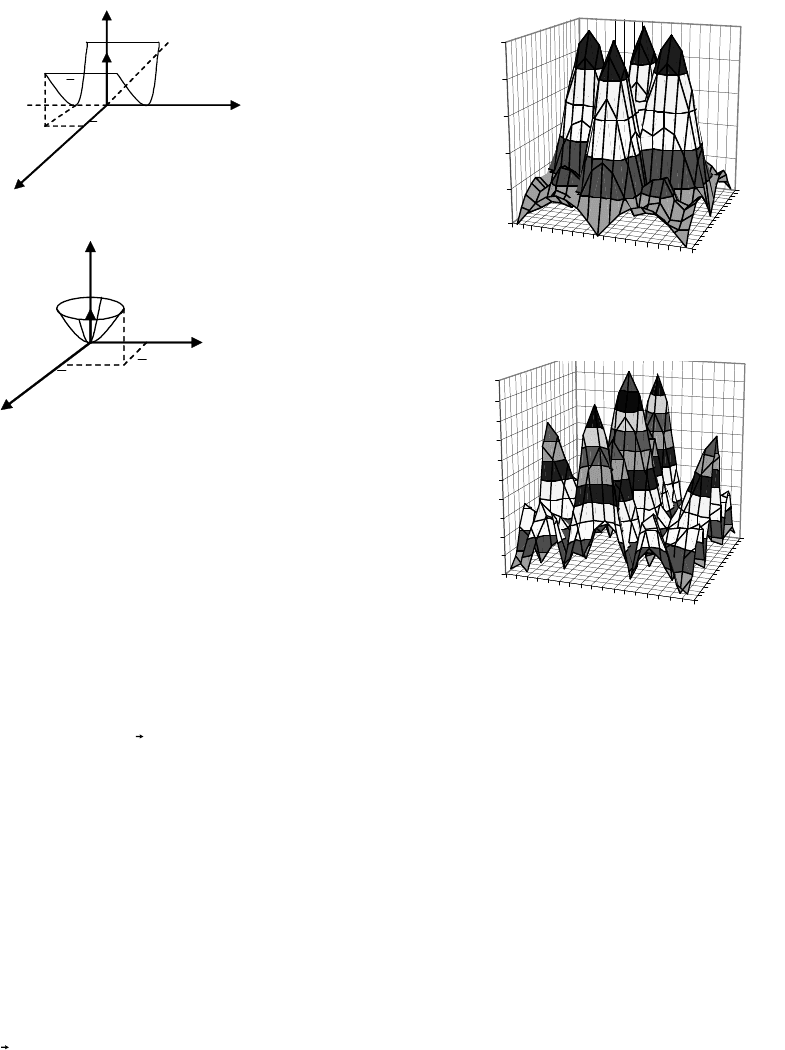
Будем искать распределения поверхностной плот-
ности тока на следующих структурах: идеально прово-
дящий плоский экран (рис. 4); зеркало в форме парабо-
лического цилиндра (рис. 5); зеркало в форме парабо-
лоида вращения (рис. 6).
x
y
z
Ω
2
a
2
a
−
2
b
2
b
−
r
′
r
Рис. 4. Идеально проводящий плоский экран.
385
x
y
z
r
′
r
Ω
2
a
2
b
−
Рис.5. Зеркало в форме параболического цилиндра.
x
y
z
r
′
r
2
a
2
a
−
Рис. 6. Зеркало в форме параболоида вращения.
Отметим, что при реализации алгоритма следует
учесть особенности каждой поверхности, т.е. преобра-
зовать уравнения, выведенные в первом разделе, с
целью наиболее удобной реализации алгоритма их
решения [6].
Результаты и обсуждение
При расчетах полагаем
(
)
001
xr
r
r
r
=
τ
,
(
)
002
yr
r
r
r
=
τ
,
(
)
00
zrn
r
r
r
=
. На рис. 7 представлено норми-
рованное распределение поверхностной плотности
тока
j
на идеально проводящем плоском экране:
ba
×
=
Ω
,
a
=
λ
,
2
=
=
ba
м,
}25.0,0,0{
'
ar =
. В каче-
стве облучателя – вертикальный ЭЭИ.
Расстояние между экстремумами (пучностями
плотности тока) равно половине длины волны, что
соответствует физическому смыслу. Полученное рас-
пределение плотности тока полностью симметрично,
как и ожидалось, т.к. вертикальный излучатель распо-
ложении строго над центром облучаемого плоского
экрана квадратной формы.
На рис.8 представлено распределение поверхно-
стной плотности тока
j
на зеркале в форме парабо-
лического цилиндра
2
axz =
,
]5.0,5.0[ aay
−
∈
,
a
=
λ
,
1
=
a
м
,
}25.0,0,0{
'
ar =
.
В
качестве
облучателя
использован
вертикаль
-
ный
ЭМИ
.
По
представленным
результатам
можно
сделать
следующий
вывод
:
в
случае
вертикального
излучателя
сечения
по
двум
различным
направлениям
поверхно
-
сти
плотности
распределения
тока
совпадают
.
1
Р1
0
0.2
0.4
0.6
0.8
1
J/Jmax
x0,a
y0,а
-1
-1
1
Рис
.7.
Нормированное
распределение
поверхностной
плотности
тока
на
идеально
проводящем
плоском
эк
-
ране
.
1
Р1
0
0.1
0.2
0.3
0.4
0.5
0.6
0.7
0.8
0.9
1
J/Jmax
x0,а
y0,а
-1/2
-1/2
1/
1/2
Рис
.8.
Распределение
поверхностной
плотности
тока
на
зеркале
в
форме
параболического
цилиндра
.
Приведенные
результаты
соответствуют
априор
-
ным
соображениям
о
характере
решения
ИУ
.
Обсуж
-
даемый
метод
вполне
применим
для
решения
задач
рассматриваемого
типа
.
Литература
1.
Никольский
,
В
.
В
.
Электродинамика
и
распро
-
странение
радиоволн
[
Текст
]/
Никольский
В
.
В
. –
М
.:
Наука
, 1973. – 607
с
.
2. Poggio A.J., Miller E.K. Integral Equation
Solutions of Three-Dimensional Scattering Problems,
Chapt. IV in Computer Techniques for Electromagnetics,
edited by Mittra R., Pergamon Press, New York, 1973. –
P. 125-132.
3.
Блатов
,
И
.
А
.
Об
алгебрах
операторов
с
псевдо
-
разреженными
матрицами
и
их
приложениях
//
Си
-
бирский
мат
.
журнал
.
Т
. 37. N 1. 1996.
стр
. 36-59.
4. Harrington, R.F. Field Computation by Moment
Method [Text]/ Harrington R.F. – Macmillan, New York,
1968 – 150 p.
5.
Алашеева
Е
.
А
.,
Блатов
И
.
А
.,
Маслов
М
.
Ю
.
Ре
-
шение
задачи
рассеяния
электромагнитного
поля
эле
-
мента
электрического
тока
проводящим
экраном
ко
-
нечных
размеров
//
Инфокоммуникационные
техноло
-
гии
,
№
2, 2007
г
.,
стр
. 8-14.
6.
Алашеева
Е
.
А
.
Анализ
излучения
двумерных
идеально
проводящих
структур
методом
интеграль
-
ных
уравнений
//
Диссертация
на
соискание
ученой
степени
кад
.
ф
-
м
.
наук
.
Самара
ПГУТИ
, 2009
г
.

386
MATHEMATICAL MODELLING IN PROBLEMS OF SETTLEMENT
FORECASTING OF THE REFLECTOR ANTENNAS NEAR
ELECTROMAGNETIC FIELDS
E.
A.
A
LASHEEVA
,
R
USSIA
,
M.
Y.
M
ASLOV
,
R
USSIA
,
D.
V.
S
KACHKOV
,
R
USSIA
Povolgskiy State University of Telecommunications and Informatics, e-mail: mike@psati.ru
In problems of settlement forecasting of near
electromagnetic fields of the reflector antennas along with a
traditional aperture method last years the approaches based
on integration of true functions of current distribution on a
reflector surface are actively developed. Thus currents are
defined by methods of the theory of diffraction.
The problem of diffraction of electromagnetic waves on not
closed surface can be reduced or to the integrated equation,
or to system of the two-dimensional integrated equations,
concerning density of the currents directed at surfaces by the
falling electromagnetic field of a kind:
( ) ( ) ( ) ( ) ( ) ( )
[ ]
{
}
,,grad
2
1
02010002
dSrrGrjrrjrНr
S
S
S
′
′′
×
′′
⋅−⋅−=×
∫
rrr
r
rrr
r
rr
r
rr
τττ
( ) ( ) ( ) ( )
( ) ( ) ( )
[ ]
{ }
. ,grad
2
1
01
0020001
dSrrGrjr
rjrrНr
S
S
S
′
′′
×
′′
⋅+
+⋅−=×−
∫
rrr
r
rr
r
r
rrr
r
rr
τ
ττ
By working out of algorithms of the numerical decision
of the integrated equations character of behaviour of
decisions in a vicinity of edges of a surface (trailer points of
a contour), as a rule, is considered.
The decision of an electrodynamic problem can be
divided into three stages. The first stage is the reception of
mathematical parities between physical sizes interesting for
us.
The given parities are turned out from Maxwell
equations in the integrated or differential form which are a
better approach to a problem.
The second stage of the decision of a problem
consists in introduction of certain restrictions on
behaviour of fields and sources on corresponding
surfaces. The various approached mathematical
models which yield reasonable results for a
physical problem can be for this purpose used.
The third stage - reception of numerical
results. For this purpose often transform the
formal decision to a kind more convenient for
carrying out of numerical calculations.
Optimum procedures of the decision
irrespective of the mathematical form demand
about identical volume of calculations for
reception of numerical result. The approach based
on the integrated equations, possesses a number
of the advantages connected with its flexibility.
In the report ways of the decision, found
wide application of a considered class of
problems are analyzed.
The special attention is given to a choice of
decomposition basis for current function. Results
of numerical modeling for near fields of antennas
with a various mirror configuration are given.
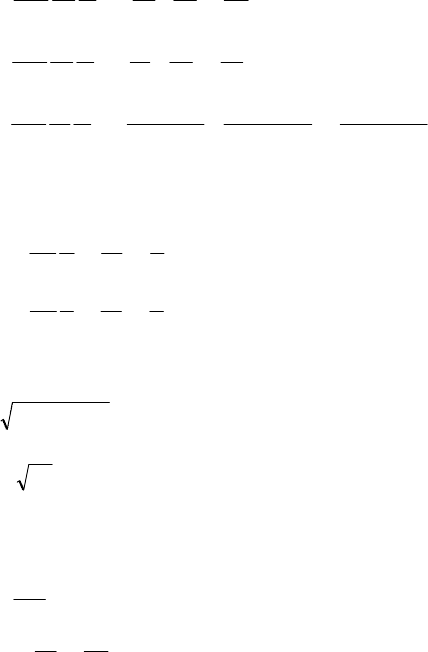
387
ФОРМИРОВАНИЕ ВОЛНОВОГО ПОЛЯ
В БЛИЖНЕЙ ЗОНЕ ИЗЛУЧАЮЩЕЙ СИСТЕМЫ
М.Ю.
М
АСЛОВ
,
Р
ОССИЯ
,
Д.В.С
КАЧКОВ
,
Р
ОССИЯ
Поволжский государственный университет телекоммуникаций и информатики, e-mail: mike@psati.ru
Аннотация.
В
прикладных задачах радиодиагностики и неразрушающего контроля весьма острой
является проблема компоновки оборудования с учетом требований к сформированному волновому
полю в рабочей области. В метровом диапазоне и диапазоне более длинных волн это сопряжено с не-
обходимостью размещения антенны на достаточно большом расстоянии от исследуемого объекта,
что не всегда удобно и возможно. Обойти это ограничение можно путем искусственного формирова-
ния волнового поля в ближней зоне антенны. В докладе приводятся результаты численного модели-
рования и обсуждаются эффекты, связанные с формированием волнового поля в области, традици-
онно определяемой как зона индукции.
Abstract. In applied problems of radio-diagnostic and nondestructive control an assembling of the equip-
ment subject to the requirements of the formed wave field in the workspace is a very important problem. At
wave-lengths up to UHF range it is connected with the need to place an antenna far enough away from in-
vestigated object, this is not always convenient and possible. To circumvent this limitation is possible by
forming an artificial wave field in near zone of the antenna. Results of numerical simulation are contained in
the report. The effects associated with the formation of the wave field in an area traditionally defined as the
zone of induction are discussed.
Введение
В прикладных задачах радиодиагностики и не-
разрушающего контроля весьма острой является про-
блема компоновки оборудования с учетом требований
к сформированному волновому полю в рабочей об-
ласти. Для сантиметрового и миллиметрового диапа-
зона решение поставленной задачи, как правило, не
составляет труда. В метровом диапазоне и диапазоне
более длинных волн это сопряжено с необходимостью
размещения антенны на достаточно большом расстоя-
нии от исследуемого объекта, что не всегда удобно и
возможно. Обойти это ограничение можно путем ис-
кусственного формирования волнового поля в ближ-
ней зоне антенны.
В докладе рассмотрены вопросы создания волно-
вого поля в ближней зоне излучающей системы путем
искусственного обеспечения синфазности электриче-
ского и магнитного полей создаваемых источниками
различной природы – электрическими токами и сис-
темами, имитирующими магнитные токи. Для про-
верки данной гипотезы рассмотрена систему апертур,
возбуждаемую в общем случае электрическими и
магнитными токами. Совокупность электрических и
магнитных токов, произвольно расположенных в
плоскости можно моделировать, используя ориги-
нальную математическую модель базового излучаю-
щего элемента - скрещенного элемента Гюйгенса
(СЭГ).
Вывод исходных уравнений
Запишем выражения для компонент вектора на-
пряженности электрического поля, создаваемого эле-
ментарным электрическим излучателем (ЭЭИ), нахо-
дящегося в центре декартовой системы координат и
ориентированного вдоль оси oz [1, стр.109]:
( )
krti
x
e
r
k
i
r
k
r
i
Il
r
xz
E
−
++−=
ω
ωπε
2
232
33
4
1
&
; (1.1)
( )
krti
y
e
r
k
i
r
k
r
i
Il
r
yz
E
−
++−=
ω
ωπε
2
232
33
4
1
&
; (1,2)
(
)
(
)
(
)
( )
krti
z
e
r
krz
i
r
krz
r
rz
i
Il
r
E
−
−
+
−
+
−
−=
ω
ωπε
222
2
22
3
22
2
331
4
1
&
. (1.3)
И выражения для компонент вектора напряжен-
ности магнитного поля:
( )
krti
x
e
r
k
i
r
Il
r
y
H
−
+−=
ω
π
2
1
4
1
&
; (2.1)
( )
krti
y
e
r
k
i
r
Il
r
x
H
−
+−=
ω
π
2
1
4
1
&
; (2.2)
0=
z
H
&
. (2.3)
где:
222
zyxr ++=
– расстояние от геометрическо-
го центра ЭЭИ до исследуемой точки пространства;
εµω
=k
– волновое число;
f
πω
2=
– циклическая частота.
Для упрощения дальнейших преобразований вы-
делим некоторые общие коэффициенты:
ikr
e
r
K
−
=
π
4
1
0
&
; (4)
( )
r
ak
i
r
a
aK +=
2
1
&
; (5)
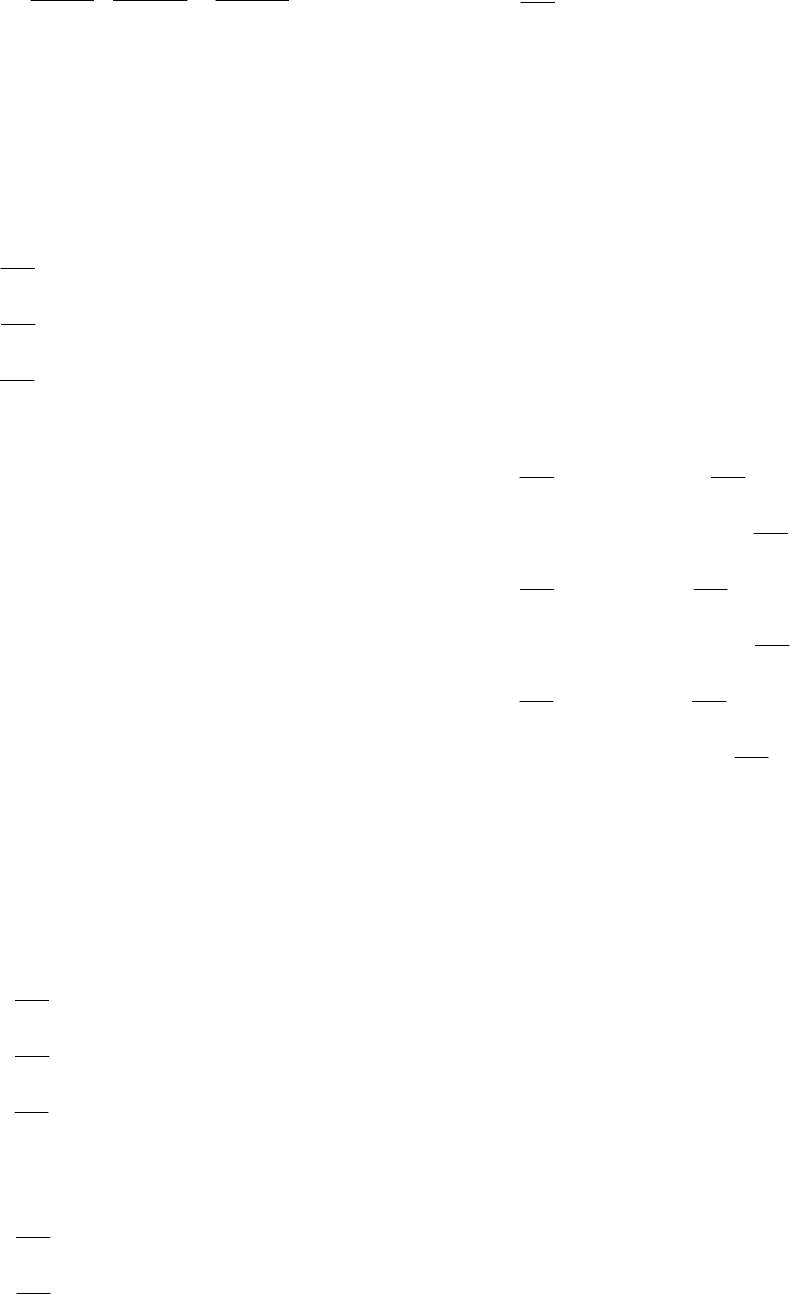
388
( )
(
)
(
)
(
)
r
kba
i
r
kba
r
ba
ibaK
2
23
2
33
,
+
+
+
+
+
−=
&
. (6)
Где a и b – функции пространства, т.е. перемен-
ных x, y и z.
От комплексных изображений перейдем к ком-
плексным амплитудам напряженностей электромаг-
нитного поля, для этого опустим множитель
ti
e
ω
.
Используя (4) и (6) можно переписать выражения
для компонент вектора напряженности электрическо-
го поля, создаваемого элементарным электрическим
излучателем в следующем виде:
( )
0,
2
0
xzK
r
K
IlE
mx
&
&
&
⋅⋅=
εω
; (7.1)
( )
0,
2
0
yzK
r
K
IlE
my
&
&
&
⋅⋅=
εω
; (7.2)
( )
22
2
0
, rzK
r
K
IlE
mz
−⋅⋅=
&
&
&
εω
. (7.3)
Используя (4) и (5) можно переписать выражения
для компонент вектора напряженности магнитного
поля, создаваемого элементарным электрическим из-
лучателем в следующем виде:
(
)
yKKIlH
mx 10
&&&
⋅⋅−=
; (8.1)
(
)
xKKIlH
my
10
&&&
⋅⋅=
; (8.2)
0=
mz
H
&
. (8.3)
Предположим, что элементарный электрический
излучатель (ЭЭИ) расположен в плоскости x0y произ-
вольным образом. Тогда его можно представить в ви-
де двух скрещенных излучателей, ориентированных
вдоль осей x и y, соответственно. Назовем такую аб-
стракцию – скрещенный элементарный электрический
излучатель (СЭЭИ). При этом следует полагать, что
по каждому из элементарных излучателей течет раз-
ный ток Ix и Iy, а поле в любой точке пространства
можно представить в виде суперпозиции полей, соз-
даваемых каждым излучателем.
Воспользовавшись поворотом системы коорди-
нат и заменой соответствующих переменных, запи-
шем выражения для компонент вектора напряженно-
сти электрического поля излучателя, ориентированно-
го вдоль оси x:
( )
22
2
0
, rxK
r
K
lIE
xxmx
−⋅⋅=
&
&
&
εω
; (9.1)
( )
0,
2
0
xyK
r
K
lIE
xxmy
&
&
&
⋅⋅=
εω
; (9.2)
( )
0,
2
0
xzK
r
K
lIE
xxmz
&
&
&
⋅⋅=
εω
. (9.3)
И выражения для компонент вектора напряжен-
ности электрического поля излучателя, ориентиро-
ванного вдоль оси y:
( )
0,
2
0
xyK
r
K
lIE
yymx
&
&
&
⋅⋅=
εω
; (10.1)
( )
22
2
0
, ryK
r
K
lIE
yymy
−⋅⋅=
&
&
&
εω
; (10.2)
( )
0,
2
0
yzK
r
K
lIE
yymz
&
&
&
⋅⋅=
εω
. (10.3)
Аналогичным образом преобразуем выражения
для компонент вектора напряженности магнитного
поля излучателя, ориентированного вдоль оси x:
0=
mx
H
&
; (11.1)
(
)
zKKlIH
xxmy
10
&&&
⋅⋅−=
; (11.2)
(
)
yKKlIH
xxmz
10
&&&
⋅⋅=
. (11.3)
И выражения для компонент напряженности маг-
нитного поля излучателя, ориентированного вдоль оси
y:
(
)
zKKlIH
yymx
10
&&&
⋅⋅=
; (12.1)
0=
my
H
&
; (12.2)
(
)
xKKlIH
yymz
10
&&&
⋅⋅−=
. (12.3)
Запишем выражения для нахождения суммарных
компонент вектора напряженности электрического
поля СЭЭИ:
( )
( )
0,,
2
0
22
2
0
xyK
r
K
lIrxK
r
K
lIE
yyxxmx
&
&
&
&
&
⋅⋅+−⋅⋅=
εωεω
;
( )
( )
[ ]
r
K
xyKlIrxKlIE
yyxxmx
εω
0
2
22
2
0,,
&
&&&
⋅⋅+−⋅=
;(13.1)
( )
( )
22
2
0
2
0
,0, ryK
r
K
lIxyK
r
K
lIE
yyxxmy
−⋅⋅+⋅⋅=
&
&
&
&
&
εωεω
;
( )
( )
[ ]
r
K
ryKlIxyKlIE
yyxxmy
εω
0
22
22
,0,
&
&&&
⋅−⋅+⋅=
;(13.2)
( ) ( )
0,0,
2
0
2
0
yzK
r
K
lIxzK
r
K
lIE
yyxxmz
&
&
&
&
&
⋅⋅+⋅⋅=
εωεω
;
( ) ( )
[ ]
r
K
yzKlIxzKlIE
yyxxmz
εω
0
22
0,0,
&
&&&
⋅⋅+⋅=
. (13.3)
И выражения для нахождения суммарных компо-
нент вектора напряженности магнитного поля СЭЭИ:
(
)
zKKlIH
yymx
10
&&&
⋅⋅=
; (14.1)
(
)
zKKlIH
xxmy
10
&&&
⋅⋅−=
; (14.2)
(
)
(
)
xKKlIyKKlIH
yyxxmz
1010
&&&&&
⋅⋅−⋅⋅=
;
(
)
(
)
[
]
011
KxKlIyKlIH
yyxxmz
&&&&
⋅⋅−⋅=
. (14.3)
Воспользовавшись принципом перестановочной
двойственности, запишем выражение для нахождения
компонент поля вблизи скрещенного элементарного
магнитного излучателя (СЭМИ) ориентированного в
плоскости xoy аналогично СЭЭИ. Для этого произве-
дем замену следующих величин:
HE
→
;
EH
→
;
µ
ε
−
→
;
M
II −→
;
где IM – магнитный ток, протекающий по маг-
нитному излучателю.

389
Запишем выражения для нахождения суммарных
компонент вектора напряженности электрического
поля СЭМИ:
(
)
zKKlIE
yMymx 10
&&&
⋅⋅−=
; (15.1)
(
)
zKKlIE
xMxmy 10
&&&
⋅⋅=
; (15.2)
(
)
(
)
[
]
011
KyKlIxKlIE
xMxyMymz
&&&&
⋅⋅−⋅=
. (15.3)
И выражения для нахождения суммарных компо-
нент вектора напряженности магнитного поля СЭМИ:
; (16.1)
( )
( )
[ ]
r
K
ryKlIxyKlIH
yMyxMxmy
µω
0
22
22
,0,
&
&&&
⋅−⋅+⋅=
; (16.2)
( ) ( )
[ ]
r
K
yzKlIxzKlIH
yMyxMxmz
µω
0
22
0,0,
&
&&&
⋅⋅+⋅=
. (16.3)
Сложив соответствующие компоненты можно
записать выражения для нахождения поля, создавае-
мого совокупностью СЭЭИ и СЭМИ, т.е. обобщен-
ным элементом Гюйгенса, произвольно ориентиро-
ванным в плоскости x0y:
(
)
(
)
( )
]
01
2
22
2
0,,
KzKlI
r
xyK
lI
r
rxK
lIE
yMy
yyxxmx
&&
&&
&
⋅⋅−
−⋅+
−
⋅=
εωεω
; (17.1)
(
)
(
)
( )
]
01
22
22
,0,
KzKlI
r
ryK
lI
r
xyK
lIE
xMx
yyxxmy
&&
&&
&
⋅⋅+
+
−
⋅+⋅=
εωεω
; (17.2)
(
)
(
)
( ) ( )
]
011
22
0,0,
KyKlIxKlI
r
yzK
lI
r
xzK
lIE
xMxyMy
yyxxmz
&&&
&&
&
⋅⋅−⋅+
+⋅+⋅=
εωεω
. (17.3)
(
)
(
)
( )
]
01
2
22
2
0,,
KzKlI
r
xyK
lI
r
rxK
lIH
yy
yMyxMxmx
&&
&&
&
⋅⋅+
+⋅+
−
⋅=
µωµω
; (18.1)
(
)
(
)
( )
]
01
22
22
,0,
KzKlI
r
ryK
lI
r
xyK
lIH
xx
yMyxMxmy
&&
&&
&
⋅⋅−
−
−
⋅+⋅=
µωµω
; (18.2)
(
)
(
)
( ) ( )
]
011
22
0,0,
KxKlIyKlI
r
yzK
lI
r
xzK
lIH
yyxx
yMyxMxmz
&&&
&&
&
⋅⋅−⋅+
+⋅+⋅=
µωµω
. (18.3)
Для нахождения поля СЭГ, сдвинутого в плоско-
сти x0y, произведем соответствующую замену коор-
динат:
xxx
′
−→
;
yyy
′
−→
;
rrr
′
−→
.
Таким образом, зная распределение электриче-
ского и магнитного токов на произвольной поверхно-
сти, расположенной в плоскости x0y, можно найти
поле в любой точке пространства, создаваемое этими
токами.
Литература
1. Айзенберг Г.З., Коротковолновые антенны.
«СВЯЗЬИЗДАТ», М.: 1962 г.
( )
( )
[ ]
r
K
xyKlIrxKlIH
yMyxMxmx
µω
0
2
22
2
0,,
&
&&&
⋅⋅+−⋅=
390
FORMATION OF THE WAVE FIELD IN NEAR ZONE OF THE
RADIATING SYSTEM
M.
Y.
M
ASLOV
,
R
USSIA
,
D.
V.
S
KACHKOV
,
R
USSIA
Povolgskiy State University of Telecommunications and Informatics, e-mail: mike@psati.ru
In applied problems of radiodiagnostics and
nondestructive control the problem of configuration of
the equipment subject to the requirements of the formed
wave field in the workspace is a very important. For
centimeter-wave and millimeter-wave solution of this
problem is not difficult usually. For meter-wave and
longer it is involves with the need to placement an
antenna far enough away from investigated object, that's
not always convenient and possibly. Work around this
limitation is possible by forming an artificial wave field
in near zone of the antenna.
In this report are discussed the issues of creating a
wave field in near zone of the radiating system by means
of artificial support in phase electric and magnetic fields
generated by sources of different nature – electric
currents and systems simulating the magnetic currents.
In order to verification this hypothesis, a system of
apertures excited in a general case electric and magnetic
currents is considered. The set of electric and magnetic
currents, arbitrary placed in the plane can be modeled
using the original mathematical model of the basic
radiating element – a crossed Huygens element.
Functions in the expressions determined by the
orientation of the emitters and their position on the
aperture.
Results of numerical simulation contained in the
report, and effects associated with the formation of the
wave field in an area traditionally defined as the zone of
induction are discussed.
