9-й Международный симпозиум по электромагнитной совместимости и электромагнитной экологии

Подождите немного. Документ загружается.

371

Из анализа рис. 1 следует, что в заданном на-

правлении прихода помех сформирован «нуль» ре-

зультирующей ДН. При этом среднее отклонение в

области боковых лепестков основной и компенсаци-

онной ДН составило -27.55 дБ, а КНД АР

84.26

КНД основной подрешетки равен

59.28

тогда

как КНД АР без компенсации, ДН которой построена

по методу амплитудно-фазового синтеза, равен

25.30

. Даже одна пара излучателей в компенса-

ционной канале позволяет сформировать провал не

только в направлении помехи, но в некоторой облас-

ти вероятного прихода помех.

На рис. 2 представлены ДН, соответствующие

приведенным на рис. 1, но при добавлении двух из-

лучателей в компенсационный канал, т.е. в компен-

сационном канале становится четыре излучателя с

номерами {10,21,31,42}. Благодаря выбору располо-

жения компенсационных излучателей удалось до-

биться снижения среднего отклонения ДН до -

27.77дБ. КНД АР повысился до

85.27

, основной

подрешетки снизился

26.28

Рис. 2.

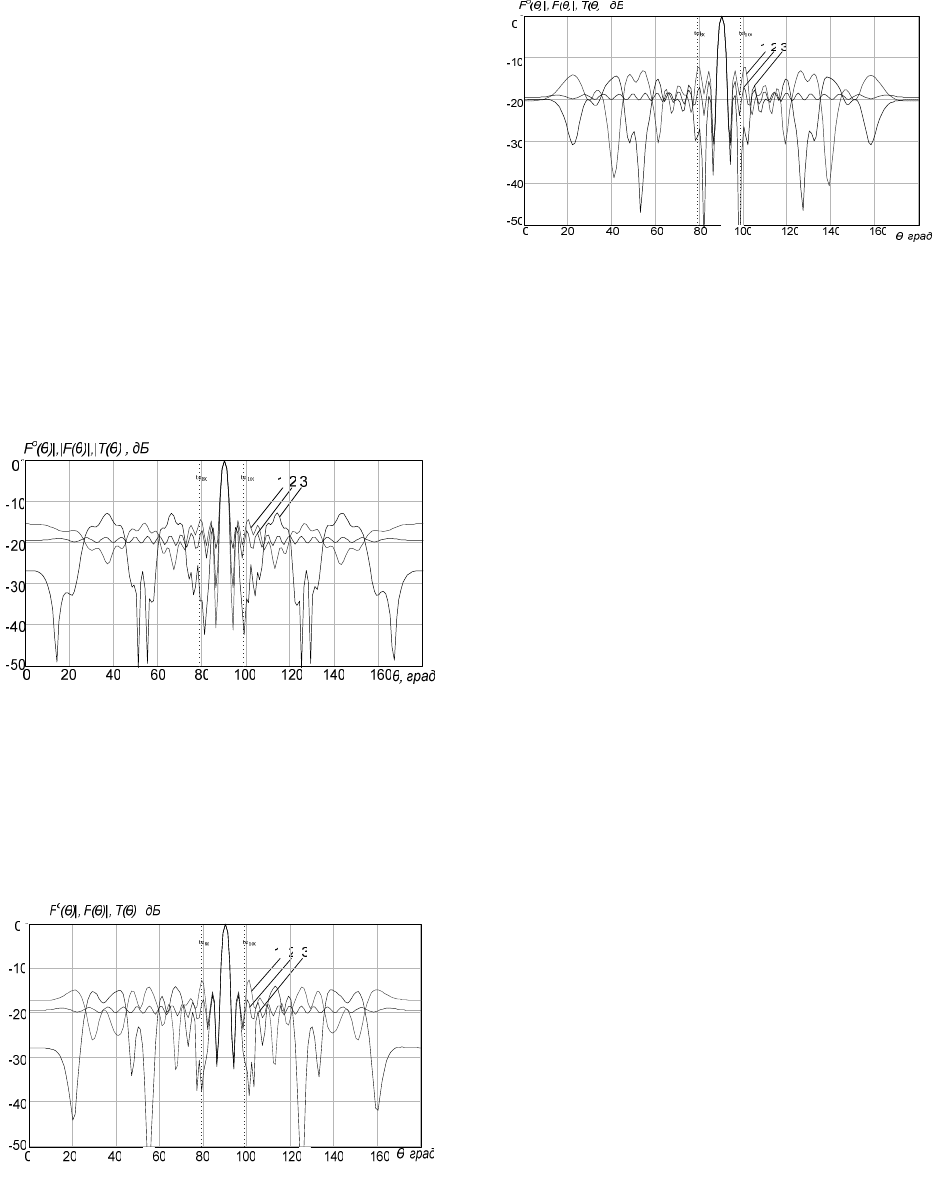
На рис. 3 представлены ДН, соответствующие

приведенным на рис. 1 и 2, но для формирования

компенсационной ДН используется 6 излучателей с

номерами {1,10,21,31,42,51}. При этом среднее от-

клонение ДН в области боковых лепестков составило

–30.24 дБ, КНД АР повысился до

24.30

, основ-

ной подрешетки снизился

55.26

Рис. 3.

Рис. 4 иллюстрирует результаты, полученные

при использовании в компенсационном канале АР 8-

ми излучателей. При этом отклонение в области бо-

ковых лепестков основной и компенсационной ДН

уменьшилось до -30.25 дБ, а КНД всей АР вырос до

27.31

, основной −

7.25

Рис. 4

Отсюда следует, что при уменьшении числа из-

лучателей в составе основной АР ее КНД уменьша-

ется, но при этом КНД всей АР возрастает.

При использовании в компенсационном канале

двух излучателей решение рассматриваемой задачи

приближается к решению задачи амплитудно-

фазового синтеза АР методом наименьших квадратов

по заданной безлепестковой ДН. Это позволяет ут-

верждать, что степень приближения ДН основной и

компенсационной АР во всей области боковых лепе-

стков ограничена. Можно добиться глубокого подав-

ления помех только в более узком секторе углов.

При проведении исследований требование (3) предъ-

являлось к УБЛ в области

5±

от направления при-

хода помех.

Заключение

Таким образом, отличие предлагаемого метода

синтеза АР с компенсацией помех от известных со-

стоит в том, что при реализации градиентной проце-

дуры искомые комплексные весовые коэффициенты

схемы суммирования определяются параллельно с

учетом требований к ДН основной и компенсацион-

ной подрешеткам АР. Полученные в настоящее вре-

мя численные результаты показывают возможность

снижения уровня боковых лепестков синтезирован-

ной АР с компенсацией помех на 15 дБ в требуемом

секторе пространственных углов при снижении ко-

эффициента направленного действия не более 15%

относительно КНД синтезированной АР с ДН без

компенсации помех. Метод позволяет также решать

задачи, связанные с выполнением требований к ДН

подрешеткам АР, например, задачи формирования

многолучевых ДН для отслеживания нескольких

целей, а также одновременного формирования не-

скольких ДН различной формы.

Литература

1. М. В. Максимов, М.П. Бобнев, Б.Х. Кривиц-

кий и др. Защита от радиопомех. М., «Сов. радио»,

1976 г., 496 с.

372

THE DECISION OF THE SYNTHESIS PROBLEM FOR ANTENNA ARRAY

WITH COMPENSATION OF THE INTERFERENCE BY THE GRADIENT

METHOD

AHOV

USSIA

ISCHENKO

USSIA

The Rostov military institute of the rocket troops,

The Rostov institute of the service and tourism, mihome@yandex.ru

Increasing to noise-immunity of the radiosystems in

condition of the powerful mutual interference often is

reached by using antennas, which realizing the method of

the compensations of the interference in practice. Broad

using of this method is in practice conditioned by its rela-

tive simplicity. However it has a defect: as a rule, method

efficient for noise-balancing within one minor lobe. The

expansion of the spatial sector of corners, in which a pos-

sibility of realization of the method is appear, is connected

with increase the number of the channel compensations of

the hindrances, that is with complication of the antenna.

In the report other approach to the problem is consid-

ered, which allows increasing the efficiency of the inter-

ference compensation method for the most simple two-

channel antenna. The interference compensation is accom-

plished by an optimization that forms radiation pattern of

antenna array for the main channel and radiation pattern of

the compensation channel in the field of minor lobe.

The difference of the proposed method of the synthe-

sis of the antenna array with compensation of the interfer-

ence from the known consists in that the sought complex

balance factors of the scheme of the summation antenna

array defined parallel with provision of requirements to

radiation pattern of the main and compensation channels

antenna array during realization gradient procedures. In

preceding work like problems of the syntheses antenna

array solve for the main channel of the antenna array with

given parameters of compensation channel of the antenna

array or, on the contrary, for compensation channel under

the known parameters of the main channel of the antenna

array with compensation of the interference.

Results of the numerical study of the proposed meth-

od with an example of the linear antenna array synthesis

are presented in report. The collation of the energy features

and parameters of the radiation pattern of the non direc-

tional lobe antenna array without compensation of the in-

terference with parameters of the synthesized antenna ar-

ray with compensation of the hindrances depending on

numbers and coordinates of the geometry of the radiation

elements of the compensation channel, chosen from com-

position antenna array, as well as depending on require-

ments to width of the ray main antenna array was con-

ducted in the course of studies.

In order to find the gradient vector of the considered

optimization problem it necessary to combine two criteri-

ons in one. The step of the approach and initial amplitude-

phase distribution is assigned. Iteration procedure of the

algorithm is concluded in incremental approximation to

required decision. Radiation patterns of the main and com-

pensation channels are calculated on each step of the itera-

tion process on the grounds of got result of decision, but

got decision is subjected on checking for performing by

the conditions. The conditions define the minimization

vector of target function. If they are executed, that got de-

cision becomes initial one and is realized transition to the

following iteration toward minimum of the target function.

If condition is not executed, that step is divided on two.

The decision which got in the course of realization of the

algorithm, with given by accuracy meets the requirements,

are presented for radiation pattern of the main and com-

pensation channels simultaneously. The resulting radiation

pattern is built by subtractions of the compensation radia-

tion pattern from the main. The part of elements is used for

shaping the compensation channel antenna array for deci-

sion of the problem of the noise-balancing. The choice of

the geometry of the elements of compensation channel is

realized as follows:

1. From all variations of the location one pair of

symmetrical for the centre antenna array elements, is cho-

sen optimum, under which condition of the noise-

balancing and minimization of the target function under

highest value of directive gain of the antenna array is exe-

cuted.

2. One more pair of elements, chosen in accordance

with condition of the point 1, is added in compensation

channel. The accompaniment of new pairs of elements can

be realized until requirement of directive gain of the an-

tenna array is executed.

The numerical results show the possibility of the re-

duction of the minor lobe level of the synthesized antenna

array with compensation of the interference on 15 dB in all

sector spatial corners by reduction of the directional lobe

not more than 15% comparatively with the directivity fac-

tor of the synthesized antenna array with non-lobe radia-

tion pattern without the interference compensation. Here-

with 15% of elements were chosen in compensation chan-

nel from composition source antenna array.

373

ИСПОЛЬЗОВАНИЕ РАССЕИВАТЕЛЕЙ СПЕЦИАЛЬНОЙ ФОРМЫ

ДЛЯ УЛУЧШЕНИЯ ЭЛЕКТРОМАГНИТНОЙ СОВМЕСТИМОСТИ

РАДИОЭЛЕКТРОННЫХ СИСТЕМ

Е.

Д.

ЕЗУГЛОВ

ОССИЯ

Д.

АБРИЭЛЬЯН

ОССИЯ

Ростовский технологический институт сервиса и туризма (филиал) ФГБОУ ВПО ЮРГУЭС, sim-ka@mail.ru

Аннотация. Проведено исследование распределения поверхностного электрического тока и полей в

ближней и дальней зоне при дифракции электромагнитных волн на селективных структурах в виде

цилиндра со звездным контуром. Проанализированы возникающие эффекты и дана их физическая

трактовка.

Abstract. The investigation of distribution surface electric current and fields in the near and far region in

diffraction of electromagnetic waves on selective structure is carried out in the paper. The structure is star-

shaped cylinder. Occurring effects are analyzed and physical insights are presented.

Введение

Одно из возможных направлений решения во-

просов электромагнитной совместимости радиоэлек-

тронных систем (РЭС) является использование на-

правленных свойств антенн, входящих в состав РЭС.

Как известно, значительную роль в формировании

направленных свойств излучения антенн (диаграмм

направленности) играют несущие конструкции, на

которых устанавливаются излучающие элементы.

Таким образом, улучшение ЭМС и ЭМЭ в усло-

виях плотного размещения РЭС связано с совершен-

ствованием антенн радиодиапазона, в частности, с

применением структур, реализующих пространст-

венные частотно-селективные свойства, что позволя-

ет расширить диапазон управления характеристика-

ми излучения и рассеяния антенн.

Построение таких структур рассматривается в

большом количестве работ, например, [1-10]. В то же

время данные структуры, как правило, предназначе-

ны для реализации фактически двух состояний – или

полного отражения электромагнитных волн, или

прохождения волн практически без отражения. Для

построения антенн частотно селективные структуры

такого типа не находят применения.

Для построения антенн, позволяющих улучшить

ЭМС и ЭМЭ необходимо использовать селективные

структуры, обеспечивающие полное отражение элек-

тромагнитных волн с переменным по фазе коэффи-

циентом отражения. При этом коэффициент отраже-

ния должен изменяться с частотой, а законы измене-

ния должны быть различными для вертикальной и

горизонтальной поляризации.

Одним из вариантов построения таких частотно

селективных структур (ЧСС) является цилиндриче-

ская поверхность, поперечное сечение которой имеет

звездный контур.

Целью доклада является анализ основных зако-

номерностей распределения полей в ближней и

дальней зоне при дифракции E- и H-поляризованной

волны на идеально проводящем цилиндре со звезд-

ным контуром.

Результаты исследований

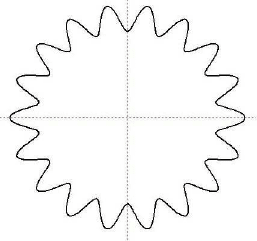
Рассмотрим бесконечный вдоль образующей

идеально проводящий цилиндр с поперечным сече-

нием в виде звезды, на который падает плоская E-

или H-поляризованная волна. Контур поперечного

сечения, показанный на рис. 1, описывается уравне-

нием

(

)

ϕϕ

NRRR cos)(

∆+=

, (1)

где

NRR , ,

∆

- геометрические параметры контура.

Рис. 1.

С направления, определяемого углом

, на ци-

линдр падает плоская волна, вектор напряженности

электрического или магнитного поля во фронте ко-

торой ориентирован вдоль образующей цилиндра.

Требуется определить распределение полей в ближ-

ней и дальней зоне, включая и распределение плот-

ности электрического тока на поверхности цилиндра.

Вид интегральных уравнений, к которым сво-

дится решение краевой задачи при дифракции E- и

H-поляризованных волн, приведен в [1–14]. Решение

интегральных уравнений проводится с учетом

периодичности законов распределения полей и то-

ков, а также параметров цилиндрической структуры

[13].

Результаты исследований диаграммы рассеяния

плоской H-поляризованной волны рассматриваемой

ЧСС представлены на рис. 2–4. Радиус цилиндра

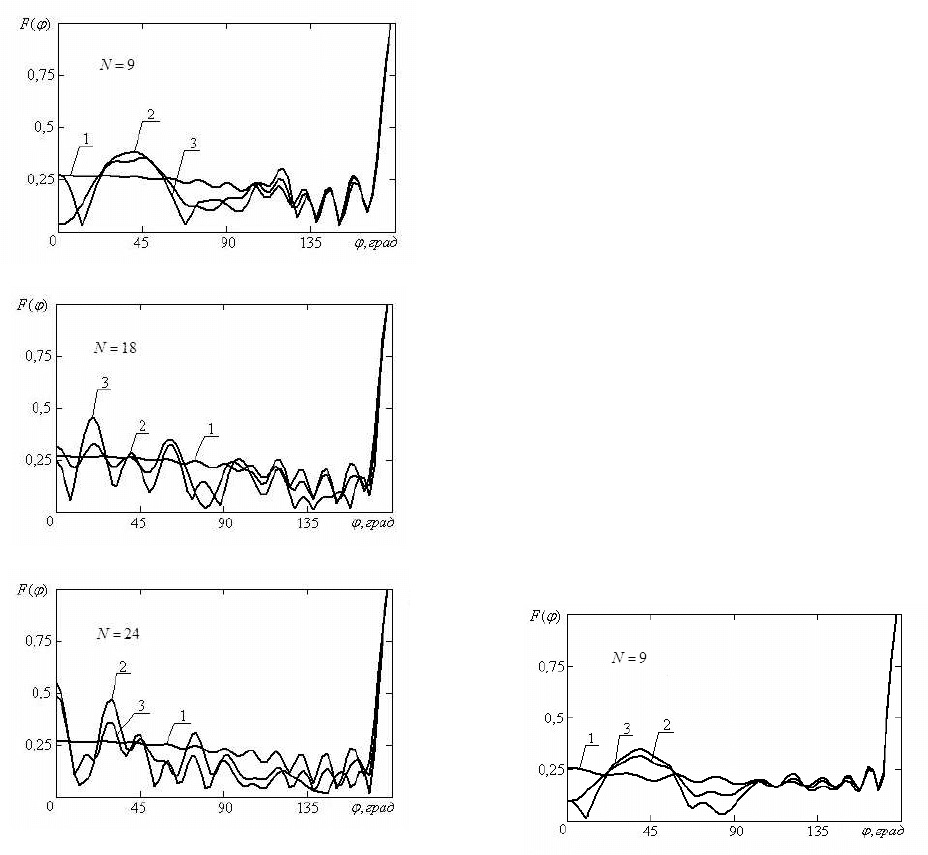
374

составлял

25.2

, параметр N выбирался 9, 18 и 24

соответственно. Кривые 1-3 на каждом рисунке по-

лучены при

∆

(круговой цилиндр),

15.0

∆

25.0

∆

соответственно.

Рис. 2.

Рис. 3.

Рис. 4.

При определенном сочетании параметров кон-

тура

∆

между комплексными амплитудами

полей в канавках возникает сдвиг фаз, обеспечи-

вающий возникновение поверхностных волн.

Необходимо подчеркнуть, что амплитуды и фазовые

скорости возникающих поверхностных волн зависят

от глубины и периода следования гребней на цилин-

дре (параметра N). Возникновение поверхностных

волн и зависимость их амплитуд и фазовых скоро-

стей от параметров звездного контура определяет

наличие пространственных селективных свойств

структур в виде цилиндра со звездным контуром.

Возбуждение поверхностных волн приводит к

появлению осцилляций диаграммы рассеяния за ис-

ключением главного лепестка. С точки зрения при-

менения селективных структур данный эффект озна-

чает возможность управления полем рассеяния при

изменении геометрических параметров контура.

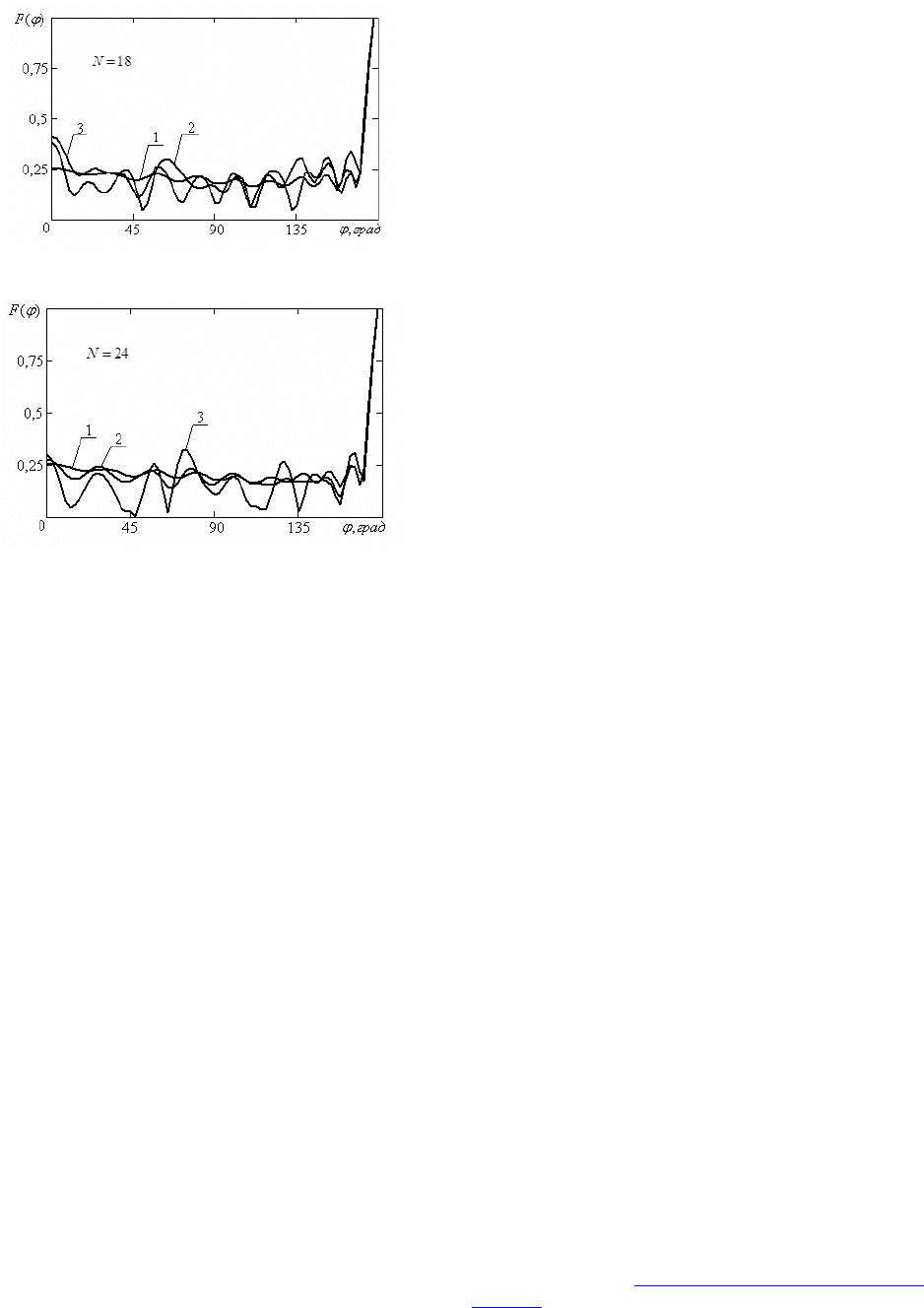
Аналогичные результаты исследований диа-

граммы рассеяния, полученные для случая дифрак-

ции E-поляризованной волны при различных значе-

ний параметров контура, приведены на рисунках 5-7.

Значения параметров

∆

выбирались таки-

ми же, как и соответствующие значения для преды-

дущего случая.

Анализ приведенных зависимостей показывает,

что, как и в случае дифракции H-поляризованной

волны для цилиндра со звездообразным контуром в

формировании диаграммы рассеяния значительно

больший вклад вносят азимутальные гармоники с

высокими номерами. Увеличение амплитуды таких

гармоник обусловлено интерференцией падающей

волны и отраженных от дна канавок волн. Амплиту-

да и фаза отраженных волн значительно изменяются

в зависимости от значений параметров

∆

Существующая ярко выраженная зависимость связа-

на с тем, что E-поляризованная волна достигает

только глубины, на которой расстояние между стен-

ками канавки приблизительно равно критическому

размеру плоского волновода для волны типа ТЕ.

Дальше амплитуда поля в направлении дна канавки

быстро уменьшается. Таким образом, фаза возни-

кающей отраженной волны существенным образом

зависит от

∆

, следствием чего является воз-

никновение частотно-селективных свойств такой

структуры.

Рис. 5.

Однако при дифракции E-поляризованной вол-

ны амплитуда возникающих осцилляций значитель-

но меньше, что определяется меньшим затеканием

токов в область тени.

375

Рис. 6.

Рис. 7.

При определенном сочетании параметров кон-

тура

∆

между комплексными амплитудами

полей в канавках возникает сдвиг фаз, обеспечи-

вающий возникновение поверхностных волн.

Необходимо подчеркнуть, что амплитуды и фазовые

скорости возникающих поверхностных волн зависят

от глубины и периода следования гребней на цилин-

дре (параметра

). Возникновение поверхностных

волн и зависимость их амплитуд и фазовых скоро-

стей от параметров звездного контура определяет

наличие пространственных селективных свойств

структур в виде цилиндра со звездным контуром.

Таким образом, в докладе рассмотрены особен-

ности рассеяния падающей плоской H- и E-

поляризованной электромагнитной волны на струк-

туре в виде идеально проводящего цилиндра со

звездным контуром. Проанализированы особенности

дифракции волн обеих поляризаций, связанные с

условиями их распространения в волноводах попе-

речного сечения. Приведено объяснение возникаю-

щих физических явлений, связанных с особенностя-

ми возбуждения высших гармоник поверхностного

электрического тока и соответственно изменением

диаграммы рассеяния.

Материалы, помещённые в доклад, выполнены в

рамках работы по аналитической ведомственной це-

левой программе «Развитие научного потенциала

высшей школы (2009-2011 годы)», подраздел 2.1.2.

«Проведение фундаментальных исследований в об-

ласти технических наук» на тему «Теоретические

основы решения задач управления–идентификация–

оценивания на основе объединенного принципа мак-

симума».

Литература

1. Вайнштейн Л.А. Электромагнитные волны.

М.: Радио и связь, 1988. 440с.

2. Y. Cai and Y. Jay. Guo. Dipole Uniform Circular

Array Backed By a Cylindrical Reflector // Asia-Pacific

Conference on Communications, pp. 1-5, 2006.

3. Z. Chudy, and L. Kachel, “Direction finding de-

vice with eight element circular antenna array”, 17th

International Conference on Microwaves, Radar and

Wireless Communications, pp. 1-4, 1921 May, 2008.

4. B. Sheleg, “A matrix-fed circular array for con-

tinuous scanning”, Proceedings of the IEEE, vol. 56, no.

11, pp. 2016-2027, 1968.

5. P. Ioannides, and C. A. Balanis, «Uniform Circu-

lar Arrays for Smart Antennas», IEEE Antennas and

Propagation Magazine, vol. 47, no. 4, pp. 192-206, 2005.

6. J-A Tsai, and B. D. Woerner, “Adaptive beam-

forming of uniform circular array (UCA) for wireless

CDMA system”, 35th Asilomar Conference on Signals,

Systems and Computers, 2001.

7. J. Zhou, L. J. Dong, M. W. Huang, and Hisakazu

Kikuchi, “Performance of MIMO with circular antenna

array using correlation matrix”, Asia-Pacific Conference

on Communications, pp. 1-5, 2006.

8. S.L. Prosvirnin, S. Zouhdi. Multi-layered arrays

of conducting strips: switchable photonic band

gap structures. Int. J. Electron. Commun., 2001, v. 55,

no. 4, pp. 260-265.

9. S.L. Prosvirnin, S.A. Tretyakov, P.L. Mla-

dyonov, Electromagnetic wave diffraction by planar

periodic gratings of wavy metal strips. J. Electromag-

netic Waves and Applications, vol. 16, no.

3, pp. 421-435, 2002.

10. Mitchell A., Kokotoff D.M., Austin M.W.

Closed-form expressions for the numerical dispersion

and reflection in FEM simulations involving // IEEE

Trans. Antennas and Propag. 2001. AP-49, №2. С.158-

164.

11. Кюркчан А.Г., Зимнов М.Х. Связь между ан-

теннами в присутствии ребристых структур // Радио-

техника и электроника. 1985. Т.30. №12. С. 2308-

2315.

12. Габриэльян Д.Д. и др. Особенности дифрак-

ции Е- и Н-поляризованных волн на цилиндре со

звездным контуром // Электромагнитные волны и

электронные системы. 2010. Т.15. №5. С. 19-21.

13. Лабунько О.С. Строгий метод в задачах ди-

фракции на цилиндрах с учетом свойств

−

пе-

риодичности // Электромагнитные волны и элек-

тронные системы. 2009. Т.14. №5. С.18-20.

14. Canto J.R. et all. Effects of losses in layered

structure containing DPS and DNG media // PIER

Online. 2008. v.4 №5. P.546-550. [Электронный ре-

сурс]: URL:

http://www.jpier.org/PIER/pier.php?

volume=85. (дата обращения 20.09.2010г.).

376

USE OF SCATTERERS OF THE SPECIAL FORM

FOR IMPROVEMENT OF ELECTROMAGNETIC COMPATIBILITY

RADIO-ELECTRONIC SYSTEMS

EZUGLOV

USSIA

D.G

ABRIEL

’

YAN

USSIA

Rostov technology institute of service and tourism, sim-ka@mail.ru

Improvement EMC and EME in the conditions of

dense placing radio-electronic means is connected with

perfection of antenna of radio frequency range, in par-

ticular, with application of the structures realizing spatial

frequency-selective properties. Existing frequency-

selective structures are intended for realization actually

two conditions – or full reflection of electromagnetic

waves, or passage of waves practically without reflec-

tion. At creation of antenna it is frequency selective

structures of this kind practically aren't applied.

For construction of the aerials, that allow improving

EMC and EME, it is necessary to use the selective struc-

tures providing full reflection of electromagnetic waves

with variable on a phase in coefficient of reflection. Thus

the reflection coefficient should change with frequency,

and change laws should be various for vertical and hori-

zontal polarization. One of variants of construction of

such selective structures is the cylindrical surface which

cross-section section has a star contour.

The basic laws of distribution of fields in a near and

far zone at diffraction E- and the H-polarized waves on

perfectly conducting cylinder with star game-round are

analyzed in the report.

The contour of cross-section section is described by

the equation

(

)

ϕϕ

NRRR cos)(

∆+=

where

NRR , ,

∆

- geometrical parameters of a contour.

Cases of excitation flat wave, a vector of intensity

electric are considered or a magnetic field in which front

is focused along forming the cylinder.

The basic result of researches is distribution of ab-

sent-minded fields in a distant zone – the dispersion dia-

gram.

For an establishment of the basic laws the cylinder

which contour was defined by parameters was consid-

ered

25.2

at values

∆

, the equal

15.0

2.0

25.0

Occurrence of polarizing-selective properties in the

given structure is connected with distinction of distribu-

tion TE- and the TM-polarized waves. The contour of

considered structure in a radial direction represents set of

wave guides of variable cross-section. At diffraction the

TM-polarized waves always will reach a bottom of

deepening though their phase speed will change at vari-

ous of width of deepening. At the same time the TE-

polarized waves can not reach a deepening bottom if the

width of deepening is less than critical size.

The specified features lead to occurrence of superfi-

cial waves and occurrence of azimuthal harmonics with

high numbers. Thus in the shined area distribution of

amplitude of a superficial current has strongly pro-

nounced oscillatory the character, bending around which

coincides with distribution of a superficial current to the

circular cylinder.

Change of a phase of a superficial current in the

shined area and in the field of a shade for the circular

cylinder of the considered radius has almost linear char-

acter depending on a corner

. For the cylinder with a

star contour at

15.0

∆

in the shined area the phase

of distribution of density of a surface current remains

almost linear, however changes more slowly that testifies

to excitation of "slow" waves. Considerable reduction of

amplitude of density of a current at diffraction of the TE-

polarized wave in the directions corresponding to direc-

tions on a bottom of flutes, is connected by that the fal-

ling wave at the specified parameters of structure does

not reach a flute bottom. It is caused by that the TE-

polarized wave reaches only depths, on which distance

between flute walls to the approximately equally critical

size of a flat wave guide for a wave of type TE. Further

the field exponential fades.

It is necessary to underline that the amplitudes and

phase speeds of arising superficial waves depend, as

appears from resulted above the analysis, from depth and

the period of following of crests on the cylinder (pa-

rameter N). Occurrence of superficial waves and de-

pendence of their amplitudes and phase speeds from pa-

rameters of a star contour defines presence of spatial

selective properties for structures in the form of the cyl-

inder with a star contour.

377

АНАЛИЗ СТРУКТУРЫ ЭЛЕКТРОМАГНИТНОГО ПОЛЯ

В ПРИСУТСТВИИ НЕСУЩЕЙ КОНСТРУКЦИИ

С РАДИОПОГЛОЩАЮЩИМ ПОКРЫТИЕМ

М. Ю. З

ВЕЗДИНА

, Р

ОССИЯ

, Ю.

А.

ВЕЗДИНА

, Р

ОССИЯ

, С. Н. З

АБЕЛКИН

, Р

ОССИЯ

А.

В.

ОДЗОРОВ

, Р

ОССИЯ

, А. Н.

АМОДЕЛОВ

, Р

ОССИЯ

Ростовский технологический институт сервиса и туризма (филиал)

ГОУ ВПО «Южно-Российский государственный университет экономики и сервиса»,

e-mail: zvezdina_m@mail.ru

Ростовский военный институт ракетных войск им. М.И. Неделина, e-mail: exus201@mail.ru

Южно-Российский государственный университет экономики и сервиса, e-mail:

samodelov@gmail.com

Аннотация. Приводится алгоритм решения задачи дифракции на круговом металлическом цилиндре

с покрытием, основывающийся на использовании метода окаймления с учетом диагональной матри-

цы неизвестных спектральных коэффициентов разложения поля. Показано, что полученное аналити-

ческое представление обратной матрицы дает возможность не только значительно сократить вычис-

лительные затраты при моделировании структуры возбуждаемого поля, но и проводить полноволно-

вой анализ данного поля. Приводятся результаты исследований влияния параметров двухслойного

покрытия на характеристики диаграммы рассеяния металлического цилиндра при падении на него

плоской волны.

Abstract. The algorithm of diffraction problem solution on circular coated metal cylinder is given. The al-

gorithm is based on the bordering method with an account of diagonal matrix of unknown spectral coeffi-

cients of field expanding. It is shown that the obtained analytic representation allows not only reducing the

computational costs significantly when simulating the structure of the excited field, but also carrying out the

full-waveform analysis of the field under investigation. The investigation results for the two-layer coating

parameters influence on the directivity pattern characteristics for the metallic cylinder with incident plane

wave are given.

Введение

Одним из направлений повышения электромаг-

нитной совместимости радиоэлектронных средств

является применение радиопоглощающих покрытий

[1]. В целях обеспечения их широкополосной работы

покрытия выполняются в виде многослойных, а для

улучшения поглощающих характеристик в качестве

материалов все чаще используются метаматериалы с

магнитодиэлектрическими свойствами. Разнообразие

способов реализации данных материалов и покрытий

из них обусловливает необходимость использовать

при моделировании свойств покрытия решения зада-

чи дифракции электромагнитной волны на металли-

ческом теле с покрытием, полученные в замкнутой

форме. Такая форма записи решения дает возмож-

ность проводить полноволновой анализ структуры

возбуждаемого электромагнитного поля.

Известные решения задачи дифракции электро-

магнитной волны, несмотря на каноническую форму

поверхности тела, не рассматривают случай метал-

лического кругового цилиндра резонансных разме-

ров с многослойным магнитодиэлектрическим по-

крытием. В связи с этим в докладе приводится алго-

ритм решения подобной задачи, полученный на ос-

нове использования метода окаймления с учетом

диагонального характера матрицы неизвестных

спектральных коэффициентов разложения поля.

Описание модифицированного метода

окаймления

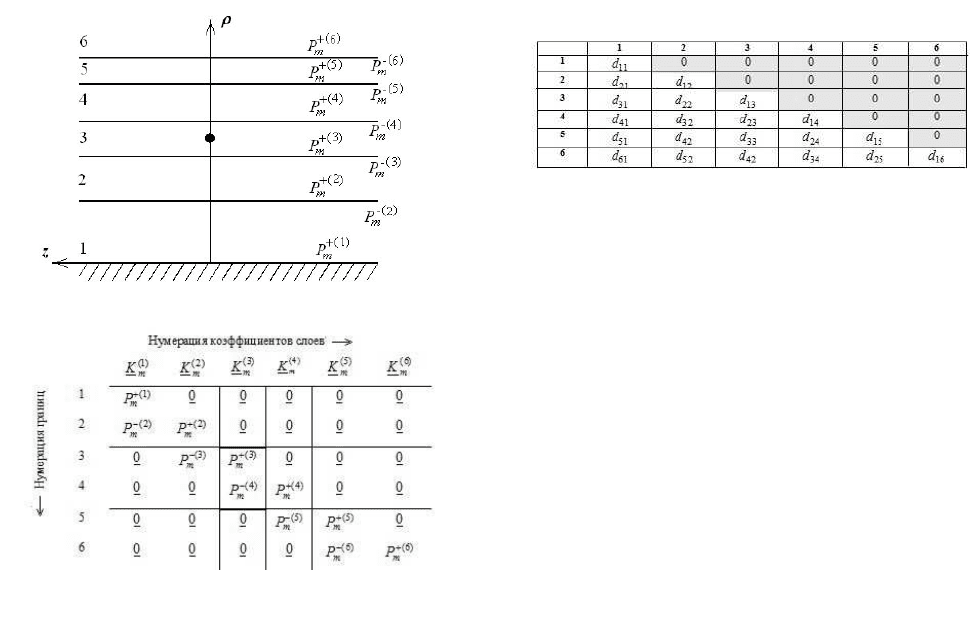
Применение метода окаймления для решения

задачи дифракции рассмотрим для частного случая,

когда покрытие, расположенное на круговом метал-

лическом цилиндре выполнено из

слоев, отсчет

которых осуществляется снизу (от поверхности ме-

таллического цилиндра) вверх. Верхний,

-й

слой, представляет собой свободное пространство.

Сторонний источник размещается в

−

м слое по-

крытия (

1,,2,1

Mj K

Необходимо

найти

реше

ние

задачи

дифракции

возбуждаемой

волны

на

теле

данной

конфигурации

Предположим

для

конкретности

что

покрытие

имеет

пять

слоев

(

сторонний

источник

располагается

слое

номером

«3»,

как

показано

на

рис

.1.

378

Для рассматриваемого случая матрица неиз-

вестных коэффициентов спектрального разложения

электромагнитных полей имеет диагональный вид,

приведенный на рис.2. Утолщенными линиями пока-

зан слой со сторонним источником. Блочные элемен-

ты

][

)( j

][

)( j

−

определяют тангенциальные

компоненты электрического и магнитного полей на

верхней (знак «+») и нижней (знак «-») поверхностях

−

го слоя покрытия. Выражения для данных блоч-

ных элементов приведены в работе [2].

Для получения обратной матрицы неизвестных

коэффициентов спектрального разложения полей

применим метод окаймления [3]. С учетом двухдиа-

гонального характера исходной матрицы использо-

вание метода окаймления для совокупности первых

четырех верхних блочных элементов

исходной

матрицы выражение для обратной матрицы имеет

вид:













−













−−−

−

111

DCAD

. (1)

Применяя последовательно указанное соотно-

шение к последующим элементам ленты, несложно

представить полную обратную матрицу в виде, пока-

занном на рис.3. Матрица является нижней тре-

угольной и диагональной. Элементы

(

1,,2,1

Mi K

) главной диагонали обратной мат-

рицы определяются соотношением:

(

)

)(

−

. (2)

На

-й (

1,,3,2

Mj K

)

поддиагонали

−

элемент

может

быть

найден

использованием

соот

ношения

( )

( ) ( )

dPPd

)1(













−=

∏

−+−

−

−++

. (3)

Для

рассматриваемой

пятислойной

структуры

получаем

следующие

значения

элементов

матрицы

на

главной

(

первой

)

диагонали

(

)

)(

(

−

Pdiagd

, (4)

на

второй

поддиагонали

(

)

(

)

(

)

)1()2(

)2(

−

+−

−

−=

mmm

PPPd

(

)

(

)

(

)

)2()3(

)3(

−

+−

−

−=

mmm

PPPd

(

)

(

)

(

)

)3()4(

)4(

−

+−

−

−=

mmm

PPPd

(

)

(

)

(

)

)4()5(

)5(

−

+−

−

−=

mmm

PPPd

(

)

(

)

(

)

)5()6(

)6(

−

+−

−

−=

mmm

PPPd

, (5)

на

третьей

поддиагонали

(

)

(

)

(

)

(

)

(

)

)1()2(

)2()3(

)3(

−

+−

−

+−

−

mmmmm

PPPPPd

(

)

(

)

(

)

(

)

(

)

)2()3(

)3()4(

)4(

−

+−

−

+−

−

mmmmm

PPPPPd

(

)

(

)

(

)

(

)

(

)

)3()4(

)4()5(

)5(

−

+−

−

+−

−

mmmmm

PPPPPd

(

)

(

)

(

)

(

)

(

)

)4()5(

)5()6(

)6(

−

+−

−

+−

−

mmmmm

PPPPPd

, (6)

на

четвертой

поддиагонали

(

)

(

)

(

)

(

)

×−=

−

+−

−

+ )3(

)3()4(

)4(

41 mmmm

PPPPd

(

)

(

)

(

)

)1()2(

)2(

−

+−

−

mmm

PPP

(

)

(

)

(

)

(

)

×−=

−

+−

−

+ )4(

)4()5(

)5(

42 mmmm

PPPPd

(

)

(

)

(

)

)2()3(

)3(

−

+−

−

mmm

PPP

(

)

(

)

(

)

(

)

×−=

−

+−

−

+ )5(

)5()6(

)6(

43 mmmm

PPPPd

(

)

(

)

(

)

)3()4(

)4(

−

+−

−

mmm

PPP

, (7)

на

пятой

поддиагонали

(

)

(

)

(

)

(

)

(

)

×=

−

+−

−

+−

−

)3()4(

)4()5(

)5(

51 mmmmm

PPPPPd

(

)

(

)

(

)

(

)

)1()2(

)2()3(

−

+−

−

+−

mmmm

PPPP

(

)

(

)

(

)

(

)

(

)

×=

−

+−

−

+−

−

)4()5(

)5()6(

)6(

52 mmmmm

PPPPPd

(

)

(

)

(

)

(

)

)2()3(

)3()4(

−

+−

−

+−

mmmm

PPPP

, (8)

на

шестой

поддиагонали

Рис

.1.

Геометрия

покрытия

Рис

. 2

Структура

исходной

матрицы

Рис

.3.

Вид

обратной

матрицы

379

(

)

(

)

(

)

(

)

(

)

×=

−

+−

−

+−

−

)4()5(

)5()6(

)6(

61 mmmmm

PPPPPd

(

)

(

)

(

)

××

−

+− )3(

)3()4(

mmm

PPP

(

)

(

)

(

)

)1()2(

)2(

−

+−

−

mmm

PPP

. (9)

Неизвестные коэффициенты разложения поля

могут быть получены путем простого умноже-

ния обратной матрицы на вектор-столбец правой

части )(F

)(F][K

−

. (10)

Определитель исходной матрицы коэффициен-

тов

][

, используемый для формулировки характе-

ристического уравнения системы, может быть полу-

чен через определители диагональных элементов

матрицы [4]:

(

)

∏

)(

det])det([

. (11)

Анализ полученных соотношений

Выполним оценку полученных выражений (2)-(9)

для элементов обратной матрицы с точки зрения воз-

можности получения аналитического решения. Учиты-

вая граничные условия на поверхности слоев, имеем,

что все блочные элементы, кроме элементов

)1(+

)1( ++ M

, являются квадратными невырожденными

матрицами. Первый и последний элементы являются

прямоугольными матрицами размерности

соответственно. Поскольку операция обращения опре-

делена только для квадратных невырожденных матриц,

то для указанных элементов матрицы

(

)

)1(

−

(

)

)1(

−

++ M

являются псевдообратными [4, 5].

Для псевдообратной матрицы используем об-

ращение Мура-Пенроуза, в соответствии с которым

псевдообратная матрица

][

(обобщенная обратная

матрица Мура-Пенроуза) для матрицы

][A

размер

ностью

определяется

соотношением

[5]:

(

)

**][

AAAA

−

. (12)

Символом

«*»

обозначены

операции

транспо

нирования

комплексного

сопряжения

Получаемая

псевообратная

матрица

будет

иметь

размерность

будет

определена

однозначно

если

противном

случае

псевдообратная

мат

рица

может

быть

определена

неоднозначно

[5].

Выполненная

оценка

вычислительных

затрат

связанных

нахождением

коэффициентов

разложе

ния

полей

показала

что

применение

предложенного

решения

полученного

использованием

метода

окаймления

позволяет

при

использовании

свойства

исходной

матрицы

(

ее

ленточного

характера

)

не

хра

нить

исходную

матрицу

размерности

−

памяти

непосредственно

использовать

получен

ные

соотношения

для

нахождения

неизвестных

ко

эффициентов

разложения

Анализ

структуры

поля

присутствии

по

крытия

последнее

время

при

разработке

радиопо

глощающих

покрытий

все

чаще

стали

применяться

метаматериалы

на

основе

композитов

включения

ми

виде

металлических

структур

[6].

Особенно

стью

данных

материалов

является

изменение

элек

тродинамических

параметров

частотном

диапазо

не

от

положительных

до

отрицательных

значений

относительных

диэлектрической

магнитной

про

ницаемостей

связи

этим

были

проведены

иссле

дования

влияния

параметров

материала

покрытия

на

характеристики

рассеяния

–

диаграмму

рассеяния

(

ДР

) -

металлического

кругового

цилиндра

радиуса

Таблицах

приведены

результаты

ис

следований

для

двухслойных

покрытий

толщиной

слоя

1,0=

(

2,1

)

для

случаев

падения

волн

поляризации

Параметры

материала

слоев

выби

рались

из

возможных

значений

проницаемостей

ма

териала

частотном

диапазоне

Анализ

полученных

результатов

показал

что

возбуждение

поверхностных

волн

возможно

только

случае

выполнения

верхнего

слоя

покрытия

из

опти

чески

более

плотных

материалов

(

варианты

1, 4, 6).

Однако

поверхностная

волна

полюсом

ik 05,1/

(

поперечное

волновое

число

λπ

вол

новое

число

свободного

пространства

длина

волны

свободном

пространстве

)

возбуждается

толь

ко

при

падении

волны

поляризации

ее

вклад

полное

поле

дальней

зоне

проявляется

виде

незна

чительных

осцилляций

амплитуды

поля

Таблица

1 –

Характеристики

ДР

металлического

цилиндра

покрытием

поляризация

Параметры

покры

тия

max

дБ

УБЛ

дБ

θθ

град

№

2.0

;

-1,9 -8,7 25,6/4,8

№

;

2.0

0,59 -9,1 20,0/4,9

№

;

2,0

-1,6 -9,2 20,1/4,7

№

2,0

;

-1,39 -9,5 20,1/4,7

№

;

2.0

2,0

0,3 -9,3 20,1/4,8

№

2.0

2,0

;

-2,1 -9,3 24,9/4,7

380

Таблица 2 – Характеристики ДР металлического

цилиндра с покрытием Е-поляризация

Параметры покры-

тия

max

дБ

УБЛ,

дБ

θθ

град

№1:

2.0

;

-2,87 -9,1 26,2/5,0

№2:

;

2.0

-1,29 -10,6 21,8/4,9

№3:

;

2,0

-0,54 -10,0 19,8/5,0

№4:

2,0

;

-1,43 -10,4 21,8/5,0

№5:

;

2.0

2,0

-0,58 -10,8 19,7/5,0

№6:

2.0

2,0

;

-1,6 -10,3 21,8/5,1

В общем случае выполнение двухслойных по-

крытий дает больше возможностей управлять струк-

турой рассеиваемого электромагнитного поля по

сравнению с использованием однослойных покры-

тий. Минимальный уровень рассеиваемого поля не-

зависимо от поляризации волны достигается, когда

верхний слой покрытий выполняется из оптически

более плотного материала, чем нижний. Причем при

использовании в качестве слоя-подложки метамате-

риала с относительными диэлектрической и магнит-

ной проницаемостями меньшими единицы можно

обеспечить дополнительной снижение уровня рас-

сеиваемого поля для вариантов 1 и 6 для волны Н-

поляризации - на 0.2 дБ, для волны Е-поляризации –

на 0,3 дБ.

Уровень задних лепестков может быть снижен

для волны Н-поляризации - на 5..7 дБ, для волны Е-

поляризации – на 2..3 дБ по сравнению с данным

показателем однослойного покрытия. Ширина глав-

ного лепестка ДР сужается в среднем на 7 градусов

по сравнению с данным показателем цилиндра без

покрытия.

Минимальный уровень рассеиваемого цилин-

дром поля в направлении на просвет для Е-

поляризации падающей волны может быть обеспе-

чен путем выбора таких параметров двухслойного

покрытия, чтобы полное отражение на нижней гра-

нице покрытия наступало при меньших углах паде-

ния.

Заключение

Полученные результаты позволяют сделать

следующие выводы;

- решение в замкнутой форме системы уравне-

ний, описывающих решение задачи дифракции на

металлическом круговом цилиндре с многослойным

покрытием, записанное в виде спектрального разло-

жения полей может быть получено с использованием

метода окаймления при учете вида матрицы (ее

двухдиагонального характера).

- достоинствами предложенного решения явля-

ются: независимость получаемого решения от распо-

ложения стороннего источника относительно слоев

покрытия; получение в явном виде обратной матри-

цы и вследствие этого значительное снижение вы-

числительных затрат;

- в качестве недостатка следует отметить неод-

нозначность обратной матрицы при переходе от за-

писи в виде блочных матриц к элементам;

- возможным вариантом исключения указанно-

го недостатка является разбиение исходной матрицы

на квадратные блоки меньшей размерности (не

);

- выполнение покрытий из метаматериалов на

основе композитных материалов с металлическими

включениями в виде двухслойных дает больше воз-

можностей управлять структурой рассеиваемого

электромагнитного поля по сравнению с использова-

нием однослойных покрытий;

- минимальный уровень рассеиваемого цилин-

дром поля в направлении на просвет для Е-

поляризации падающей волны может быть обеспе-

чен путем выбора таких параметров двухслойного

покрытия, чтобы полное отражение на нижней гра-

нице покрытия наступало при меньших углах паде-

ния.

Литература

1. Актуальные вопросы исследований распро-

странения радиоволн, электромагнитной совмести-

мости, антенно-фидерных устройств средств радио-

связи и радиовещания. / Под ред. Г.И. Трошина //

Антенны. 2002. Вып.8-9 (63).

2. Zvezdina M.Yu. et all. Analytic Conversions in

Diffraction Problems on Metal Cylinders with Multilayer

Magnetodielectric Coating // PIERS Draft Proc.,

Moscow, Russia, 2009, August 18-21. The

Electromagnetics Academy, Cambridge, MA, P.1304-

1307, ISSN 1559-9450.

3. Воеводин В.В., Кузнецов Ю.А. Матрицы и

вычисления. М.: Наука, 1984. 320 с.

4. Гантмахер Ф.Р. Теория матриц. М.: Наука,

1988. 552 с.

5. Ланкастер П. Теория матриц. М.: Наука, 1982,

272 с.

6. Бычков И.В., Зотов И.С., Федий А.А. Иссле-

дование прохождения и отражения СВЧ-излучений в

многослойных композитных материалах

CaSO4•2H2O-графит // Письма в ЖТФ. 2010. Т.37.

Вып.14. С. 90-94.