Зубков А.М. Конспект лекций по теории случайных процессов
Подождите немного. Документ загружается.

Механико-математический факультет МГУ им. М. В. Ломоносова
А.М.Зубков
Конспект лекций
по теории случайных процессов
2008 год, 6-й семестр
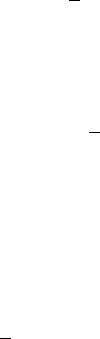
1. Введение
Теория случайных процессов — один из важнейших разделов теории
вероятностей. Теория случайных процессов выделяется из теории вероятностей более
сложной структурой множества значений, которые принимают случайные величины,
а также разнообразием способов задания вероятностной меры.
В теории вероятностей основой аксиоматики является понятие вероятностного
пространства (Ω, F, P), где Ω — пространство элементарных событий, F — σ-алгебра
измеримых подмножеств Ω, называемых событиями, P — вероятностная мера на
F. Случайной величиной ξ, принимающей значения в множестве M со своей σ-
алгеброй измеримых подмножеств G, называется любая функция ξ : Ω → M,
измеримая относительно F и G. В курсе теории вероятностей обычно считалось,
что M есть Z, R или R
n
(для векторных случайных величин или геометрических
вероятностей). В теории случайных процессов в качестве M выбирается множество
более сложной структуры. Например, если M = Z
∞
или M = R
∞
, то значениями
случайной величины ξ являются последовательности целых или действительных
чисел, и говорят, что ξ — случайный процесс с дискретным временем; если M
— пространство непрерывных функций или пространство функций без разрывов
второго рода, то говорят, что ξ — случайный процесс с непрерывным временем; если
M — пространство функций от нескольких аргументов, то говорят, что ξ — случайное
поле, и т.д. Любое конкретное значение случайной величины ξ, которое является
последовательностью или функцией, называют траекторией (или реализацией)
случайного процесса.
Четкой границы между задачами теории вероятностей и задачами теории
случайных процессов нет. Например, пусть ξ
1
, ξ
2
, . . . — последовательность
независимых одинаково распределенных случайных величин, принимающих
действительные значения, и S
n
= ξ
1
+ . . . + ξ
n
. Для последовательности сумм S
n
в курсе теории вероятностей доказываются два закона больших чисел:
Закон больших чисел. Если ξ
1
, ξ
2
, . . . независимы и одинаково распределены,
существует Mξ
1
и Dξ
1
< ∞, то для любого ε > 0
lim
n→∞
P
©
¯
¯
1
n
S
n
− Mξ
1
¯
¯
> ε
ª
= 0.
Усиленный закон больших чисел. Если ξ
1
, ξ
2
, . . . независимы и одинаково
распределены, существует Mξ
1
и Dξ
1
< ∞, то
P
n
lim
n→∞
1
n
S
n
= Mξ
1
o
= 1.
Закон больших чисел описывает свойства распределений индивидуальных сумм
S
n
. Это типичная задача теории вероятностей. В теории случайных процессов,
как правило, интересуются свойствами траектории (последовательности) S
1
, S
2
, . . .
Например, в усиленном законе больших чисел речь идет о случайной величине
η =
(
lim
n→∞
1
n
S
n
, если этот предел существует,
∗ в противном случае,
2
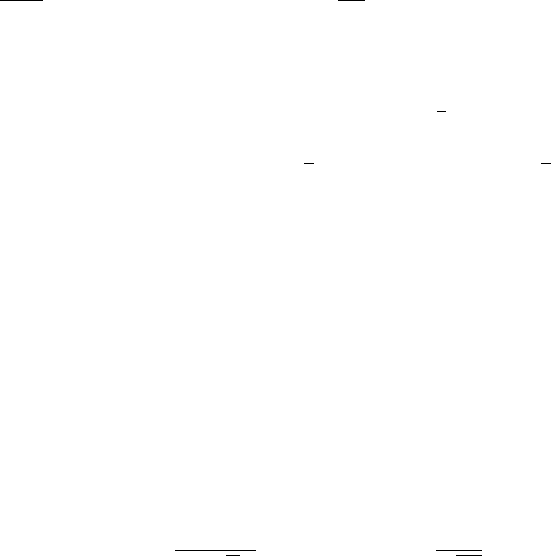
равной пределу по Чезаро последовательности {ξ
n
}.
Задачи. 1.1. Показать, что для сумм S
n
= ξ
1
+ . . . + ξ
n
, где {ξ
k
}
∞
k=1
—
последовательность независимых случайных величин, в которой ξ
k
имеет нормальное
распределение со средним 0 и дисперсией Dξ
k
= σ
2
k
, закон больших чисел не
выполняется при σ
2
k
= k
α
, α > 1, и выполняется при σ
2
k
= o(k), k → ∞.
1.2. Показать, что для сумм S
n
= ξ
1
+ . . . + ξ
n
, где {ξ
k
}
∞
k=1
— последовательность
независимых случайных величин, в которой ξ
k
имеет нормальное распределение со
средним 0 и дисперсией Dξ
k
= σ
2
k
усиленный закон больших чисел не выполняется
при σ
2
k
=
k
ln ln k
), и выполняется при σ
2
k
=
k
ln k
.
1.3. Показать, что для последовательности независимых случайных величин {ξ
k
}
с нулевыми математическими ожиданиями и распределениями
P{ξ
k
= 1} = P{ξ
k
= −1} =
1
2
, k 6= n!,
P{ξ
n!
= n!} = P{ξ
n!
= −n!} =
1
n
, P{ξ
n!
= 0} = 1 −
2
n
, n = 1, 2, . . . ,
обычный закон больших чисел выполняется, а усиленный — не выполняется.
2. Закон повторного логарифма
Пусть ξ
1
, ξ
2
, . . . — независимые одинаково распределенные случайные величины с
Mξ
k
= a, |a| < ∞, Dξ
k
= σ
2
< ∞,
и S
n
= ξ
1
+ . . . + ξ
n
, n = 0, 1, . . . , – случайное блуждание. Для S
n
справедлива
центральная предельная теорема:
lim
n→∞
P
½
S
n
− na
σ
√
n
≤ x
¾
= Φ(x) =
1
√
2π
x
Z
−∞
e
−u
2
/2
du.
Однако это утверждение относится только к распределениям отдельных значений S
n
и мало что говорит о свойствах всей последовательности {S
n
}.
Пусть ζ
1
, ζ
2
, . . . – произвольная последовательность случайных величин
(возможно, зависимых), ψ(n) — детерминированная функция. Будем через χ{A} =
χ{A}(ω) обозначать индикатор события A. Рассмотрим случайную величину
ν(ψ) =
X
n≥1
χ{ζ
n
≥ ψ(n)}
— число элементов последовательности ζ
1
, ζ
2
, . . ., лежащих выше графика функции
ψ(n).
Определение. Функция ψ(n) называется верхней функцией максимумов для
последовательности случайных величин {ζ
n
}, если P{ν(ψ) < ∞} = 1, и нижней
функцией максимумов, если P{ν(ψ) = ∞} = 1.
3

Функция ψ(n) называется правильной верхней границей последовательности
случайных величин {ζ
n
}, если существует такая функция ε(n) = o(max{1, |ψ(n)|}),
n → ∞, что функция ψ(n) + ε (n) — верхняя, а функция ψ(n) − ε(n) — нижняя
функция максимумов.
Аналогично определяются нижняя и верхняя функции минимумов и правильная
нижняя граница.
Утверждение 2.1. Пусть {ζ
n
} — последовательность независимых случайных
величин, имеющих стандартное нормальное распределение с математическим
ожиданием 0 и дисперсией 1 :
P{ζ
n
≤ x} = Φ(x) =
x
Z
−∞
ϕ(u)du, ϕ(u) =
1
√
2π
e
−u
2
/2
, n = 1, 2, . . .
Тогда
P
½
lim sup
n→∞
ζ
n
√
2 ln n
= 1
¾
= 1 и P
½
lim inf
n→∞
ζ
n
√
2 ln n
= −1
¾
= 1.
Замечания. а) Так как P{|ζ
n
| > x} > 0 для любого x < ∞, то P{ζ
n
> f(n)} > 0
для любого n и любого значения f(n) < ∞.
б) Случайные величины ζ
n
одинаково распределены, но верхняя граница не равна
константе.
Таким образом, при условиях теоремы существуют правильные верхняя и нижняя
границы, равные ψ
+
(n) =
√
2 ln n и ψ
−
(n) = −
√
2 ln n.
Доказательство.
Лемма Бореля – Кантелли. Пусть на вероятностном пространстве (Ω, F, P)
задана последовательность событий {A
1
, A
2
, . . .} и
A
∗
=
n
ω ∈ Ω :
X
n≥1
χ(A
n
) = ∞
o
,
где χ(A
n
) – индикатор события A
n
.
а) Если
P
n≥1
P{A
n
} < ∞, то P{A
∗
} = 0.
б) Если события A
1
, A
2
, . . . попарно независимы и
P
n≥1
P{A
n
} = ∞, то P{A
∗
} = 1.
Доказательство леммы. Пусть ν
T
=
P
1≤n≤T
χ(A
n
) — число одновременно
происходящих событий в начальном отрезке A
1
, . . . , A
T
. Последовательность ν
T
монотонно не убывает, поэтому при каждом ω ∈ Ω существует lim
T →∞
ν
T
def
= ν =
P
n≥1
χ{A
n
} ≤ ∞. Тогда
Mν
T
=
T
X
k=1
P{A
k
}, Mν =
X
k≥1
P{A
k
} и A
∗
= {ν = ∞}.
а) Если ряд
P
n≥1
P{A
n
} сходится, то Mν < ∞ и поэтому P{ν < ∞} = 1, т.е.
P{A
∗
} = 0.
4
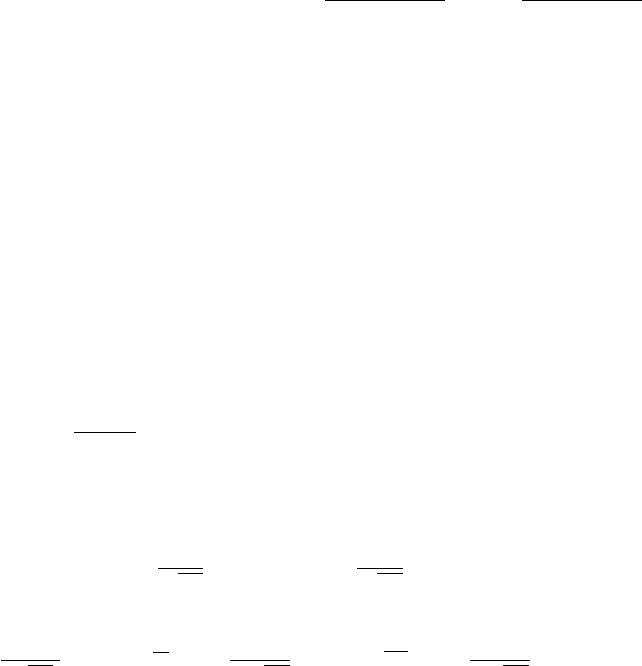
б) В силу попарной независимости событий A
n
их индикаторы тоже попарно
независимы. Следовательно, дисперсия суммы этих индикаторов равна сумме
дисперсий слагаемых:
Dν
T
= M(ν
T
− Mν
T
)
2
= M
Ã
T
X
k=1
(χ(A
k
) − P{A
k
})
!
2
=
=
T
X
k, l=1
M(χ(A
k
) − P{A
k
})(χ(A
l
) − P{A
l
}) =
=
T
X
k=1
M(χ(A
k
) − P{A
k
})
2
=
T
X
k=1
P{A
k
}(1 − P{A
k
}) ≤ Mν
T
.
Согласно неравенству Чебышева при любом a < Mν
T
P{ν
T
≥ a} = P{ν
T
− Mν
T
≥ a − Mν
T
} ≥
≥ P{Mν
T
− a ≥ ν
T
− Mν
T
≥ a − Mν
T
} =
= P{|ν
T
− Mν
T
| < Mν
T
− a} ≥ 1 −
Dν
T
(Mν
T
− a)
2
≥ 1 −
Mν
T
(Mν
T
− a)
2
.
В случае б) ν
T
↑ ν и Mν
T
↑ ∞ при T ↑ ∞, значит, при любом a < ∞
P{ν ≥ a} ≥ lim
T →∞
P{ν
T
≥ a} = 1.
Наконец,
P{ν = ∞} = P
(
∞
\
a=1
{ν ≥ a}
)
= 1
как вероятность пересечения счетной совокупности событий, вероятность каждого
из которых равна 1. Лемма доказана.
Утверждение 2.2. Справедливо соотношение
1 − Φ(x) =
1 − ε
x
x
ϕ(x), где ε
x
→ 0 при x → ∞ и ε
x
> 0 при x > 0. (1)
Доказательство. Используя замены u = x + v и vx = z, получаем
P{ζ
n
> x} =
1
√
2π
∞
Z
x
e
−u
2
/2
du =
1
√
2π
∞
Z
0
e
−(x+v)
2
/2
dv =
=
e
−x
2
/2
√
2π
∞
Z
0
e
−vx−
v
2
2
dv =
e
−x
2
/2
x
√
2π
∞
Z
0
e
−z
e
−
z
2
2x
2
dz =
e
−x
2
/2
x
√
2π
(1 − ε
x
);
5

здесь ε
x
> 0 при x > 0 и ε
x
→ 0 при x → ∞. Эти равенства следуют из соотношений
∞
Z
0
e
−z
e
−
z
2
2x
2
dz <
∞
Z
0
e
−z
dz = 1,
∞
Z
0
e
−z
e
−
z
2
2x
2
dz >
√
x
Z
0
e
−z
e
−
z
2
2x
2
dz > e
−
1
2x
√
x
Z
0
e
−z
dz =
= e
−
1
2x
³
1 − e
−
√
x
´
>
¡
1 −
1
2x
¢
³
1 − e
−
√
x
´
> 1 − e
−
√
x
−
1
2x
.
Тем самым утверждение 2.2 доказано.
Рассмотрим события A
n
(b) = {ζ
n
> b
√
2 ln n}, n = 1, 2, . . . , и
A
∗
(b) =
(
X
n≥1
χ{A
n
(b)} = ∞
)
=
½
ω : lim sup
n→∞
ζ
n
√
2 ln n
≥ b
¾
.
Из независимости случайных величин ζ
n
следует независимость событий A
n
(b). Тогда
согласно лемме Бореля–Кантелли
P{A
∗
(b)} =
(
1, если
P
n≥1
P{A
n
(b)} = ∞,
0, если
P
n≥1
P{A
n
(b)} < ∞.
Исследуем условия сходимости ряда
P
n≥1
P{A
n
(b)}.
Согласно утверждению 2.2 при некоторых δ
n
= δ
n
(b) → 0 при n → ∞,
∞
X
n=1
P{A
n
(b)} =
∞
X
n=1
e
−(b
√
2 ln n)
2
/2
b
√
2 ln n
√
2π
(1 − δ
n
) =
1
b
√
2π
∞
X
n=1
1 − δ
n
n
b
2
√
2 ln n
.
Так как при b > 1 ряд в правой части сходится, а при b ∈ (0, 1] расходится, то,
используя лемму Бореля – Кантелли, получаем:
P
½
lim sup
n→∞
ζ
n
√
2 ln n
≥ b
¾
= 0 ∀b > 1 ⇒ P
½
lim sup
n→∞
ζ
n
√
2 ln n
≤ 1
¾
= 1,
P
½
lim sup
n→∞
ζ
n
√
2 ln n
≥ b
¾
= 1 ∀b < 1 ⇒ P
½
lim sup
n→∞
ζ
n
√
2 ln n
≥ 1
¾
= 1.
Наконец,
P
½
lim sup
n→∞
ζ
n
√
2 ln n
= 1
¾
= 1
как вероятность пересечения двух событий
½
lim sup
n→∞
ζ
n
√
2 ln n
≤ 1
¾
и
½
lim sup
n→∞
ζ
n
√
2 ln n
≥ 1
¾
,
вероятность каждого из которых равна 1.
6
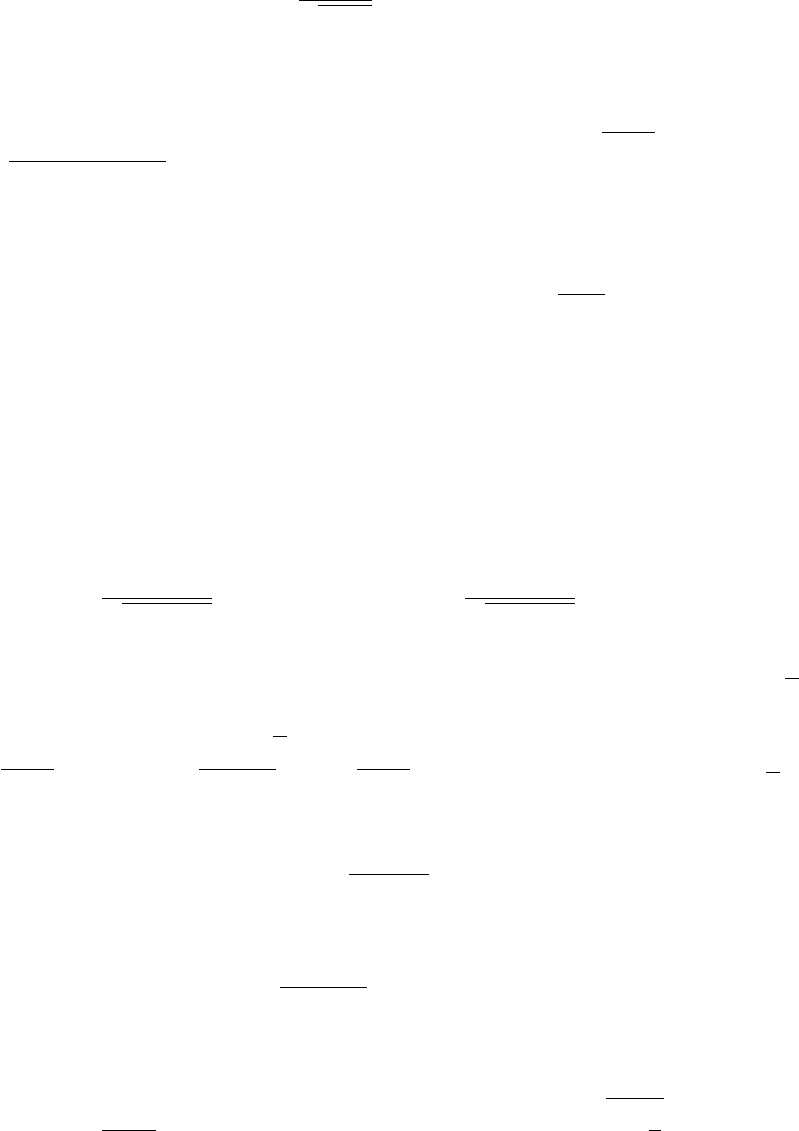
Ввиду того, что распределение случайных величин ζ
n
симметрично,
P
½
lim inf
n→∞
ζ
n
√
2 ln n
= −1
¾
= 1.
Утверждение 2.1 доказано.
Задачи. 2.1. Пусть ζ
1
, ζ
2
, . . . — независимые случайные величины, имеющие
стандартное нормальное распределение. Показать, что ψ
−
(n) =
√
2 ln n — нижняя, а
ψ
+
(n) =
p
2(ln n + ln ln n) — верхняя функции максимумов последовательности {ζ
n
}.
2.2. Пусть ξ
1
, ξ
2
, . . . — последовательность независимых случайных величин,
равномерно распределенных на отрезке [0,1]. Найти верхние и нижние функции
минимумов последовательности {ξ
n
}. Существуют ли такие верхняя функция
минимумов ψ
+
(n) и нижняя функция минимумов ψ
−
(n), что
ψ
+
(n)
ψ
−
(n)
→ 1 при n → ∞?
Докажем теперь аналогичное утверждение для последовательности S
n
= ζ
1
+. . .+
ζ
n
, n = 0, 1, . . . В отличие от Утверждения 2.1 случайные величины S
n
зависимы, и
непосредственно применять вторую часть леммы Бореля – Кантелли к событиям
вида {S
n
> b
n
} нельзя. Мы применим эту вторую часть к другим независимым
событиям, выбранным специальным образом.
Теорема (закон повторного логарифма). Если ζ
1
, ζ
2
, . . . — независимые
случайные величины, ζ
n
∼ N(0, 1), и S
n
= ζ
1
+ . . . + ζ
n
, n ≥ 1, то
P
½
lim sup
n→∞
S
n
√
2n ln ln n
= 1
¾
= 1, P
½
lim inf
n→∞
S
n
√
2n ln ln n
= −1
¾
= 1.
Замечание. Если выполнены условия теоремы, то случайная величина S
n
/
√
n
имеет стандартное нормальное распределение, т.е. распределения отдельных членов
последовательностей {ζ
n
} и {S
n
/
√
n} совпадают, но верхние функции максимумов
разные:
√
2 ln n для {ζ
n
} и
√
2 ln ln n = o
³
√
2 ln n
´
для последовательности {S
n
/
√
n}.
Доказательство. Так как распределение S
n
симметрично, то (как в Утверждении
2.1) достаточно доказать первое соотношение.
Положим M(t) = max
0≤k≤t
S
k
, h(t) =
√
2t ln ln t при t ≥ e.
Лемма 2.1. Для каждого r > 1
∞
X
k=1
P
½
M(r
k+1
)
h(r
k
)
> r
¾
< ∞.
Лемма 2.2. Для любого натурального v
∞
X
k=1
P
½
1
h(v
k
)
(S
v
k
− S
v
k−1
) > c(v)
¾
= ∞, если c(v) =
r
1 −
1
v
.
Сначала покажем, как утверждение теоремы выводится из этих лемм, а потом
докажем их.
7

Доказательство теоремы. Из леммы 2.1 и леммы Бореля–Кантелли следует,
что
P
½
lim sup
k→∞
M(r
k+1
)
h(r
k
)
≤ r
¾
= 1. (2)
Далее, если r > 1 и k(n) = [log
r
n] — такое целое число, что r
k(n)
≤ n < r
k(n)+1
, то
lim
n→∞
k(n) = ∞ и
S
n
h(n)
≤
M(r
k(n)+1
)
h(r
k(n)
)
и, значит, lim sup
n→∞
S
n
h(n)
≤ lim sup
n→∞
M(r
n+1
)
h(r
n
)
,
так как k(n) → ∞ при n → ∞. Отсюда и из (2) получаем, что при всех r > 1
P
½
lim sup
n→∞
S
n
h(n)
≤ r
¾
≥ P
½
lim sup
n→∞
M(r
n+1
)
h(r
n
)
≤ r
¾
= 1,
т. е.
P
½
lim sup
n→∞
S
n
h(n)
≤ 1
¾
= 1. (3)
Докажем теперь аналогичное (3) соотношение с заменой знака ≤ знаком ≥; из
них, как в доказательстве утверждения 2.1, будет следовать утверждение теоремы.
Пусть v > 1 — целое число. Так как случайные величины
S
v
k
− S
v
k−1
= ζ
v
k−1
+ . . . + ζ
v
k
, k = 1, 2, . . . ,
определяются значениями непересекающихся групп независимых случайных величин
ξ
j
, то они независимы. Поэтому из леммы 2.2 и леммы Бореля–Кантелли следует, что
при любом целом v > 1
P
½
lim sup
k→∞
1
h(v
k
)
(S
v
k
− S
v
k−1
) > c(v)
¾
= 1. (4)
Заметим, что h(v
k
) =
√
2v
k
ln ln v
k
= (1 + o(1))h(v
k−1
)
√
v при k → ∞. Учитывая
это соотношение, равенство (3) и симметричность распределения S
n
, получаем:
P
½
lim sup
k→∞
S
v
k−1
h(v
k
)
= lim sup
k→∞
S
v
k−1
h(v
k−1
)
√
v
≤
1
√
v
¾
= 1 =
= P
½
lim inf
k→∞
S
v
k−1
h(v
k
)
≥ −
1
√
v
¾
. (5)
Так как вероятности событий в (4) и (5) равны 1, то вероятность их пересечения
тоже равна 1. Но
{lim sup a
k
> c, lim inf b
k
> d} ⇒ lim sup(a
k
+ b
k
) > c + d.
Применяя это соотношение к a
k
=
S
v
k
−S
v
k−1
h(v
k
)
, b
k
=
S
k−1
v
h(v
k
)
и учитывая (4) и (5), находим,
что при любом целом v < ∞
P
(
lim sup
k→∞
S
v
k
h(v
k
)
≥ c(v) −
1
√
v
=
r
1 −
1
v
−
1
√
v
)
= 1. (6)
8
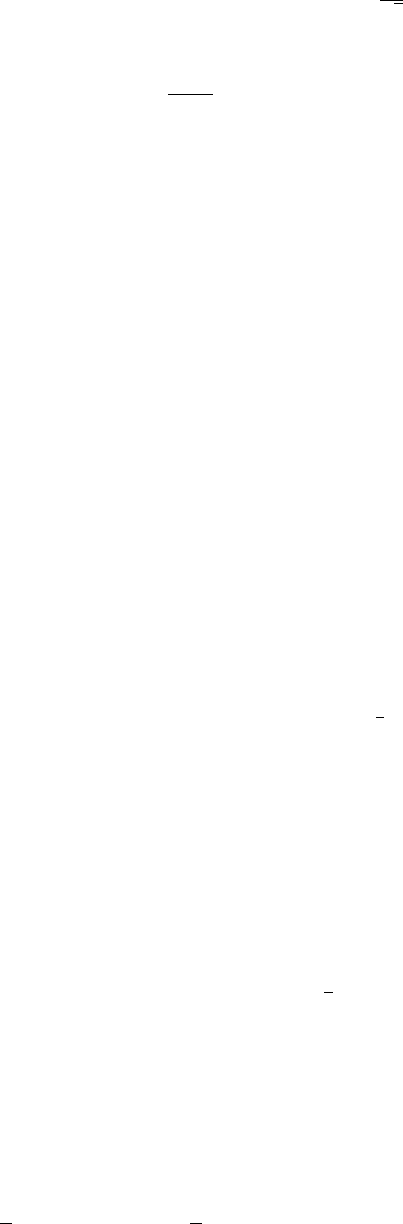
За счет выбора достаточно большого v величину c(v) −
1
√
v
можно сделать сколь
угодно близкой к 1, поэтому
P
½
lim sup
k→∞
S
n
h(n)
≥ 1
¾
= 1. (7)
Из (3) и (7) следует утверждение теоремы.
Докажем леммы 2.1 и 2.2. Начнем со вспомогательной леммы.
Лемма 2.3. Пусть ξ
1
, . . . , ξ
n
— независимые случайные величины с
симметричными распределениями: P{ξ
k
≥ x} = P{ξ
k
≤ x} при любых x ∈ R
и k ∈ {1, . . . , n}. Тогда при любом a ≥ 0
P
½
max
1≤k≤n
S
k
> a
¾
≤ 2P{S
n
> a}.
Доказательство леммы 2.3. Введем случайную величину, равную моменту
первого перехода {S
n
} через уровень a:
τ =
(
k, если S
1
, . . . , S
k−1
≤ a, S
k
> a,
n + 1, если S
1
, . . . , S
n
≤ a.
Так как ξ
1
, . . . , ξ
n
независимы и имеют симметричные распределения, то при любом
k = 1, . . . , n случайные величины S
k
= ξ
1
+ . . . + ξ
k
и S
n
− S
k
= ξ
k+1
+ . . . + ξ
n
независимы, имеют симметричные распределения и
P{S
n
− S
k
≥ 0} = P{S
n
− S
k
≤ 0} ≥
1
2
,
поскольку
P{S
n
− S
k
≥ 0} + P{S
n
− S
k
≤ 0} = 1 + P{S
n
− S
k
= 0} ≥ 1.
Учитывая эти замечания и то, что выполнение события {τ = k} определяется
значениями ξ
1
, . . . , ξ
k
и поэтому не зависит от ξ
k+1
, . . . , ξ
n
, находим:
P{S
n
> a, τ = k} ≥ P{S
n
≥ S
k
, τ = k} = P{τ = k, ξ
k+1
+ . . . + ξ
n
≥ 0} =
= P{τ = k}P{ξ
k+1
+ . . . + ξ
n
≥ 0} ≥
1
2
P{τ = k}.
Теперь, используя формулу полной вероятности, несовместность событий {τ = k}
и равенство {1 ≤ τ ≤ n} = {max(S
1
, . . . , S
n
) > a}, получаем
P{S
n
> a} =
n
X
k=1
P{S
n
> a, τ = k} ≥
≥
1
2
n
X
k=1
P{τ = k} =
1
2
P
½
max
1≤k≤n
S
k
> a
¾
.
Лемма 2.3 доказана.
9
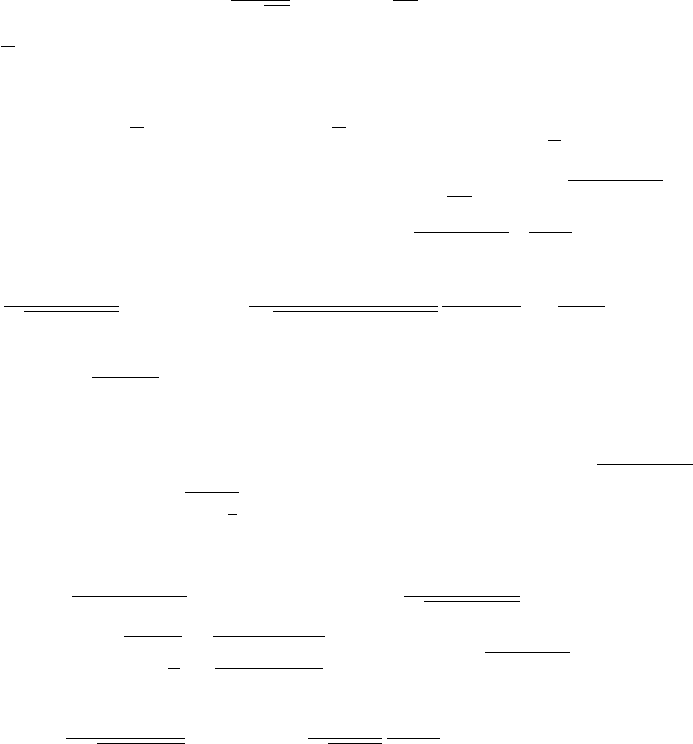
Доказательство леммы 2.1. Используя лемму 2.3, оценку (1) для хвоста
нормального распределения в виде
1 − Φ(u) ≤
1
u
√
2π
e
−u
2
/2
<
1
2u
e
−u
2
/2
и то, что S
n
/
√
n ∼ N(0, 1), поскольку S
n
∼ N(0, n), получаем, что при u > 0 и любом
натуральном n
P
©
M(n) > u
√
n
ª
≤ 2 P
©
S
n
> u
√
n
ª
= 2 P{ζ
1
> u} <
1
u
e
u
2
/2
.
Применим эту формулу при фиксированном r > 1, k >
10
ln r
и u =
√
2r ln ln r
k
:
P{M(r
k+1
) > rh(r
k
)} = P
n
M(r
k+1
) >
√
2r ln ln r
k
√
r
k+1
o
≤
≤
1
√
2r ln ln r
k
e
−r ln ln r
k
=
1
p
2r(ln k + ln ln r)
1
(k ln r)
r
<
C(r)
k
r
.
Значит, ряд
P
k→∞
P
n
M(r
k+1
)
h(r
k
)
> r
o
сходится при любом r > 1. Лемма 2.1 доказана.
Доказательство леммы 2.2. Пусть целое v > 1 фиксировано. Случайная
величина S
v
k
− S
v
k−1
имеет нормальное распределение с нулевым математическим
ожиданием и дисперсией v
k
− v
k−1
, т. е. распределена так же, как ζ
1
√
v
k
− v
k−1
. Для
каждого v > 1 при c(v) =
q
1 −
1
v
в силу оценки (1) для 1 − Φ(u) справедливо
соотношение
P
½
S
v
k
− S
v
k−1
h(v
k
)
> c(v)
¾
= P
½
ζ
1
>
c(v)h(v
k
)
√
v
k
− v
k−1
¾
=
= P
(
ζ
1
>
r
1 −
1
v
r
2v
k
ln ln v
k
v
k
− v
k−1
)
= P
n
ζ
1
>
√
2 ln ln v
k
o
∼ (8)
∼
1
2
√
π ln ln v
k
e
−ln ln v
k
∼
1
√
π ln k
1
k ln v
, k → ∞.
Таким образом, ряд, составленный из вероятностей (49), расходится. Тем самым
лемма 2.2 доказана и доказательство закона повторного логарифма завершено.
3. Цепи Маркова
Случайные процессы, названные впоследствии цепями Маркова, впервые были
рассмотрены в работах А.А.Маркова 1906–1907 гг., посвященных анализу свойств
последовательности гласных и согласных букв в русском тексте.
Пусть ξ
0
, ξ
1
, ξ
2
, . . . — произвольная последовательность случайных величин,
принимающих значения из множества {1, 2, . . . , n}. По определению условных
вероятностей для любого t > 0
P{ξ
0
= i
0
, ξ
1
= i
1
, . . . , ξ
t
= i
t
, ξ
t+1
= i
t+1
} = (9)
= P{ξ
0
= i
0
}
t
Y
s=0
P{ξ
s+1
= i
s+1
|ξ
0
= i
0
, . . . , ξ
s
= i
s
}.
10
