Зубков А.М. Конспект лекций по теории случайных процессов

Подождите немного. Документ загружается.

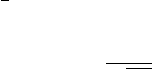
случайного процесса с такими конечномерными распределениями не существует.

Например, если

P{ξ(1) = m, ξ(2) = n} =

, m, n ∈ {0, 1},

P{ξ(2) 6 x, ξ(3) 6 y} = Φ(x)Φ(y), Φ(x) =

√

2π

−∞

−u

du,

то из первого условия следует, что P{0 < ξ(2) < 1} = 0, а из второго — что

P{0 < ξ(2) < 1} = Φ(1) − Φ(0) > 0. Значит, эти условия противоречивы, и

случайный процесс ξ(1), ξ(2), ξ(3), . . . с такими двумерными распределениями не

может существовать.

Чтобы исключить подобные ситуации, вводят понятие семейств согласованных

распределений. Условия согласованности имеют простой смысл: если вероятность

какого-либо события можно вычислять по разным конечномерным распределениям,

то эти вычисления должны давать один и тот же результат. Формально

(для случайных процессов, принимающих действительные значения) условия

согласованности записываются следующим образом.

Пусть имеется семейство конечномерных распределений

P = {P

,...,t

, t

< . . . < t

, n = 1, 2, . . .};

распределение P

,...,t

соответствует вероятностной мере на R

и, в частности,

определяет меры P

,...,t

...

×A

) на прямых произведениях борелевских

множеств A

⊂ R. Семейство P называется согласованным, если для любых двух

наборов (t

< . . . < t

) и (s

< . . . < s

) и построенного по ним набора

< . . . < v

): {v

, . . . , v

} = {t

, . . . , t

} ∩ {s

, . . . , s

при любых борелевских множествах C

, . . . , C

⊂ R справедливы равенства

,...,v

, . . . , C

) = P

,...,t

, . . . , A

) = P

,...,s

, . . . , B

где

(

, если t

= v

R в противном случае,

(

, если s

= v

R в противном случае.

Возможность задания случайного процесса конечномерными распределениями

обосновывается теоремой Колмогорова, доказательство которой можно найти,

например, в учебнике А.А.Боровкова [1].

Реализации случайного процесса ξ(t), t ∈ R, можно рассматривать как точки

в бесконечномерном пространстве R

, а его конечномерные распределения — как

семейство вероятностных мер на R

. В пространстве R

можно определить σ-алгебру

борелевских множеств F

, порожденную цилиндрическими множествами вида B ×

R\N

, где B ∈ F

— любое борелевское множество в R

, N ⊂ R, — любое конечное

множество. Вероятностная мера P на R

для любого конечного множества N ⊂ R

порождает проекцию P

на R

по формуле P

(B) = P(B × R

R\N

), B ∈ F

Теорема Колмогорова о согласованных распределениях. Если на R

задано согласованное семейство вероятностных мер Q

, N ⊂ R, то на (R

, F)

существует единственная вероятностная мера P, проекция P

которой совпадает

с Q

для любого конечного множества N ⊂ R.

Определение. Процессом с независимыми приращениями называется такой

случайный процесс ξ(t), что при любом наборе чисел t

< t

< . . . < t

вектор

приращений

∆(t

, . . . , t

) = (ξ(t

) − ξ(t

), . . . , ξ(t

) − ξ(t

n−1

))

имеет независимые координаты.

Ввиду независимости приращений при фиксированном значении ξ(t) траектория

процесса на полуоси (t, ∞) не зависит от его траектории на (−∞, t). Поэтому

процессы с независимыми приращениями являются марковскими. Более того,

поскольку приращения процесса не зависят от его текущего значения, постольку

вероятности его переходов однородны по пространству.

Чтобы описать распределения процесса с независимыми приращениями,

достаточно сопоставить каждой паре чисел s, t (s < t ) распределение приращения

ξ(t) − ξ(s). Если распределение ξ(t) − ξ(s) зависит только от t − s, то говорят, что

ξ(t) — процесс с независимыми однородными приращениями.

Для процессов с независимыми приращениями условие согласованности можно

переформулировать так: для любых t

< . . . < t

распределение ξ(t

)−ξ(t

) совпадает

с распределением суммы δ

+ . . . + δ

n−1

независимых случайных величин, где

k−1

имеет такое же распределение, как ξ(t

) − ξ(t

k−1

), k = 2, 3, . . . , n.

Задача 5.1. Доказать, что указанное условие обеспечивает согласованность

семейства конечномерных распределений процессов с независимыми приращениями.

Разумеется, условие согласованности заметно ограничивает возможности выбора

распределений приращений.

6. Пуассоновские процессы

Одной из возможностей выбора согласованных распределений для процессов с

независимыми приращениями являются пуассоновские распределения: если ν(t) —

процесс с независимыми приращениями и при любых s < t приращение ν(t) − ν(s)

имеет распределение Пуассона с параметром λ(t − s):

P{ν(t) − ν(s) = k} =

(λ(t − s))

−λ(s−t)

, k = 0, 1, . . . , λ > 0, (23)

то производящие функции распределений приращений имеют вид

ν(t)−ν(s)

∞

k=0

(λ(t − s))

−λ(t−s)

= e

−λ(t−s)(1−u)

, u ∈ R,

и поэтому для независимых случайных величин δ

, . . . , δ

n−1

, распределенных так

же, как соответственно ν(t

) − ν(t

), . . . , ν(t

) − ν(t

n−1

), из свойств производящих

функций следует, что

+...+δ

n−1

k=1

k+1

n−1

k=1

−λ(t

k+1

−t

)(1−u)

= e

−λ(t

−t

)(1−u)

= Mu

ν(t

)−ν(t

n−1

)

т.е. такие семейства распределений действительно согласованы.

Определение. Случайный процесс с независимыми приращениями, имеющими

пуассоновские распределения, называется пуассоновским процессом. Если

распределения его приращений задаются формулой (23), то он называется

однородным (или стационарным) пуассоновским процессом с интенсивностью λ.

Более общие (неоднородные) пуассоновские процессы можно задавать монотонно

не убывающей ведущей функцией Λ(t): в таком процессе ν(t) приращения независимы

и δ

t,s

= ν(s) − ν(t) при любых t < s имеет распределение Пуассона с параметром

Λ(s) −Λ(t). Для однородного пуассоновского процесса с постоянной интенсивностью

λ, очевидно, Λ(t) = λt — линейная функция. Обратно: если ν(t) — однородный

пуассоновский процесс с интенсивностью 1, то ν

(t) = ν(Λ(t)) — пуассоновский

процесс с ведущей функцией Λ(t), т.е. неоднородный пуассоновский процесс

получается из однородного детерминированной заменой времени.

Так как приращения пуассоновского процесса принимают только целые

неотрицательные значения, то его траектории монотонно не убывают, и можно

считать, что все значения пуассоновского процесса — целые числа.

Задача 6.1. Доказать, что если ξ

(t), ξ

(t), . . . , ξ

(t) — независимые пуассоновские

процессы с ведущими функциями Λ

(t), Λ

(t), . . . , Λ

(t), то ζ(t) = ξ

(t) + ξ

(t) + . . . +

(t) — пуассоновский процесс с ведущей функцией Λ

(t) + Λ

(t) + . . . + Λ

(t).

Следующее утверждение дает полезную интерпретацию (и фактически второе

определение) пуассоновского процесса.

Утверждение 6.1. Пусть ν(t) — пуассоновский процесс с интенсивностью λ.

Тогда при h → 0

P{ν(t + h) − ν(t) = 0} = 1 − λh + o(h),

P{ν(t + h) − ν(t) = 1} = λh + o(h), (24)

P{ν(t + h) − ν(t) > 1} = o(h).

Обратно, если целочисленный случайный процесс ν(t) с независимыми

неотрицательными приращениями, распределения ν(t + h) − ν(t) которых не

зависят от t, удовлетворяет условиям (24), то ν(t ) — пуассоновский процесс с

интенсивностью λ.

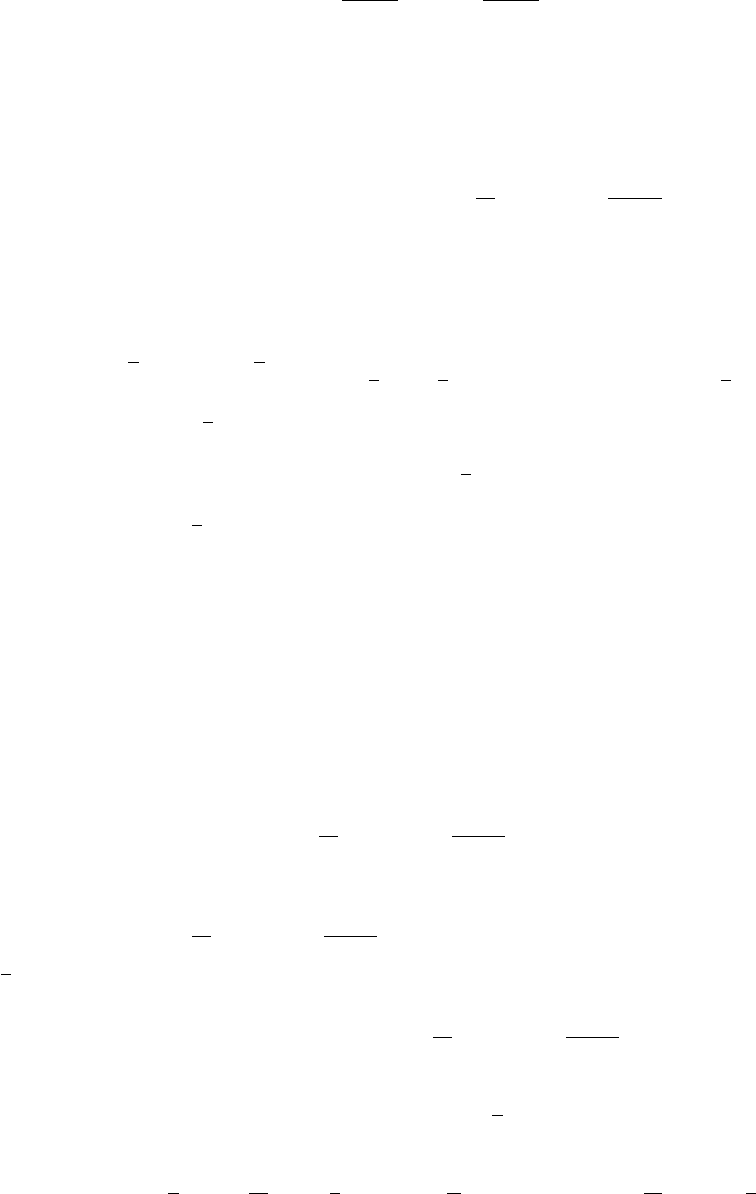
Доказательство. Первая часть утверждения следует из того, что по определению

пуассоновского процесса при любом k = 0, 1, . . .

P{ν(t + h) − ν(t) = k} =

(λh)

−λh

(λh)

(1 − λh + o(h)), h → 0.

Обратно, пусть ν(t) — целочисленный процесс с неотрицательными независимыми

приращениями, удовлетворяющий условиям (24). Покажем, что ν(t + h) − ν(t) при

любом h > 0 имеет распределение Пуассона с параметром λh. Разобьем [t, t + h) на

n полуинтервалов длины h/n. Тогда

ν(t + h) − ν(t) =

k=1

t +

− ν

t +

(k−1)h

´´

Слагаемые в этой сумме по условию независимы, одинаково распределены

и принимают целые неотрицательные значения. Производящая функция

распределения каждого слагаемого имеет вид



t+k



−ν



t+(k−1)



= 1 − λ

+ sλ

+ ε

(s) = exp

−λ(1 − s)

+ δ

(s)

где ε

(s), δ

(s) = o

при n → ∞, и в силу независимости слагаемых при любом n

ν(t+h)−ν(t)

= exp

−(1 − s)

k=1

+ nδ

(s)

. → exp{−(1 − s)λh},

Но если δ

(s) = o

при n → ∞, то выражение под знаком экспоненты стремится

к −(1 − s)λh, поэтому Ms

ν(t+h)−ν(t)

= e

−(1−s)λh

, т. е. имеет распределение Пуассона с

параметром λh, что и доказывает утверждение 6.1.

Утверждение 6.2. С вероятностью 1 все скачки пуассоновского процесса с

параметром λ < ∞ равны 1.

Доказательство. Покажем, что если ν(t) — пуассоновский процесс с параметром

λ < ∞, то для любого t и любого h > 0 математическое ожидание числа ν

(t, h)

скачков на отрезке [t, t + h], которые больше 1, равно 0. Разобьем отрезок [t, t + h] на

n равных частей и рассмотрим сумму

k=1

t +

− ν

t +

(k−1)h

> 1

def

= σ

(t, h).

Если ν

(t, h) > 1, то σ

(t, h) > 1 при любом n < ∞. С другой стороны, так как

приращения ν

t +

−ν

t +

(k−1)h

имеют распределение Пуассона с параметром

, то при n → ∞

Mσ

(t, h) =

k=1

t +

− ν

t +

(k−1)h

> 1

k=1

1 − e

−λh/n

− λ

−λh/n

k=1

+ O

− λ

1 + O

¶¶¶

k=1

= O

так как все константы в O(·) ограничены равномерно по k. Значит,

P{ν

(t, h) > 0} 6 lim

n→∞

P{σ

(t, h) > 1} 6 lim

n→∞

Mσ

(t, h) = 0,

что и требовалось доказать.

Из утверждений 6.1 и 6.2 следует, что траектория пуассоновского процесса

полностью определяется монотонно возрастающей последовательностью {ζ

}

k∈Z

точек на оси (−∞, ∞) — моментов ее (единичных) скачков. При этом вероятность

появления точки в бесконечно малом интервале (t, t + dt) равна λdt, и в

непересекающихся интервалах точки появляются независимо. Для любого открытого

множества A ∈ R число точек однородного пуассоновского потока, попадающих в A,

имеет распределение Пуассона с параметром λ mes(A). Такую последовательность

точек называют (однородным) пуассоновским потоком событий с интенсивностью

λ. Неоднородному по времени пуассоновскому процессу с ведущей функцией Λ(t)

соответствует неоднородный по времени пуассоновский поток событий, в котором

вероятность появления точки в бесконечно малом интервале (t, t + dt) равна dΛ(t).

Следующие две задачи описывают две процедуры построения пуассоновских

процессов с помощью предельных переходов.

Задача 6.2. Пусть χ

(p)

, χ

(p)

, . . . — последовательность независимых случайных

величин, P{χ

(p)

= 1} = p, P{χ

(p)

= 0} = 1 − p. Показать, что конечномерные

распределения случайных процессов ξ

(t) =

16k6nt

(λ/n)

при n → ∞ сходятся к

конечномерным распределениям пуассоновского процесса с интенсивностью λ.

Иначе говоря, пуассоновский процесс можно рассматривать как предел

последовательностей однородных испытаний Бернулли при стремлении вероятности

успеха к 0 и соответствующем увеличении числа испытаний в единицу времени.

Задача 6.3. Пусть α

, α

, . . . — последовательность независимых случайных

величин, имеющих одно и то же распределение с плотностью f(x), непрерывно

дифференцируемой в окрестности точки t

, и θ(x) = 1 при x > 0, θ(x) = 0 при

x < 0. Показать, что конечномерные распределения случайных процессов

(t) = |{k ∈ {1, . . . , n} : α

∈ (t

, t

)}|

при n → ∞ сходятся к конечномерным распределениям однородного пуассоновского

процесса с интенсивностью f(t

Иначе говоря, пуассоновский процесс можно рассматривать как совокупность

моментов наступления редких независимых событий.

Например, пуассоновский процесс часто используют как модель процесса

регистрации элементарных частиц: в куске радиоактивного материала имеется

большое число атомов радиоактивного изотопа, каждый из которых (при отсутствии

цепной реакции) живет случайное время, не зависящее от времен жизни других

атомов, и распадается в случайный момент времени. Наложение большого числа

независимых событий, происходящих в случайные моменты времени, порождает (как

в задаче 6.3) процесс, близкий к пуассоновскому.

Другой пример — поток вызовов, поступающих на телефонную станцию.

Телефонов в городе много, но с большинства из них делается немного звонков.

Естественно считать, что в нормальной ситуации вызовы с разных телефонов

поступают независимо. Поэтому правдоподобной моделью потока вызовов является

пуассоновский процесс (возможно, неоднородный по времени, потому что ночью

многие спят).

Рассмотрим распределение промежутков между моментами событий в

пуассоновском потоке ν(t) на (−∞, ∞) с интенсивностью λ > 0. Для каждого

момента t ∈ R введем случайные величины

(t) = inf{u > 0 : ν(t + u) > ν(t)}, τ

−

(t) = inf{u > 0 : ν(t − u) < ν(t)}

— время ожидания первого после момента t события и время, прошедшее к моменту

t после последнего события в пуассоновском потоке соответственно.

Утверждение 6.3. Если {ν(t)}

t∈R

— пуассоновский процесс с параметром λ,

то при любом действительном t ∈ R случайная величина τ

(t) не зависит от

значений {ν(x)}

x≤t

, а случайная величина τ

−

(t) не зависит от значений {ν(x)}

x≥t

в частности, τ

(t) и τ

−

(t) независимы. При любом u > 0 справедливы соотношения

P{τ

(t) > u} = e

−λu

, P{τ

−

(t) > u} = e

−λu

Доказательство первого равенства следует из того, что

P{τ

(t) > u} = P{ν(t + u) − ν(t) = 0} = e

−u

Второе равенство доказывается аналогично. Утверждения о независимости τ

(t) от

{ν(x)}

x≤t

и τ

−

(t) от {ν(x)}

x≥t

следуют из того, что ν(x) — процесс с независимыми

приращениями.

Следствие 6.1. Промежутки между скачками однородного пуассоновского

процесса ν(t) с интенсивностью λ независимы и имеют показательное

распределение с параметром λ.

Действительно, из независимости τ

(t) от {ν(x)}

x≤t

следует, что для любого ε > 0

P{τ

(t) > u |ν(t − ε) < ν(t)} = e

−λu

Переходя в этом соотношении к пределу по ε → 0, получаем:

P{τ

(t) > u |ν(t − 0) < ν(t)} = e

−λu

т.е. промежутки между соседними скачками однородного пуассоновского процесса с

интенсивностью λ имеют показательное распределение с параметром λ.

Для доказательства независимости промежутков между скачками однородного

пуассоновского процесса с интенсивностью λ будем считать, что ν(0) = 0, τ

= 0, и

введем обозначения для моментов скачков и промежутков между ними:

= inf{t > 0 : ν(t) > k}, ζ

= τ

− τ

k−1

, k = 1, 2, . . . ,

Так как борелевские σ-алгебры в R

порождаются параллелепипедами, то достаточно

показать, что для любого натурального k > 2 и любых x

, . . . , x

, ∆

, . . . , ∆

> 0

P{ζ

∈ (x

, x

+ ∆

), j = 1, . . . , k} =

j=1

P{ζ

∈ (x

, x

+ ∆

)}. (25)

Пусть k = 2. Тогда ввиду независимости приращений пуассоновского процесса на

непересекающихся интервалах имеем

P{ζ

∈ (x

, x

+ ∆

), ζ

∈ (x

, x

+ ∆

)} =

= P

ν(x

) − ν(0) = 0, τ

∈ (x

, x

+ ∆

ν(τ

+ x

) − ν(τ

+ 0) = 0, ν(τ

+ x

+ ∆

) − ν(τ

+ x

) > 0

+∆

P{ν(t + x

) = ν(t), ν(t + x

+ ∆

) − ν(t + x

) > 0}dP{τ

6 t} =

+∆

−λx

− e

−λ(x

+∆

)

−λt

λdt =

−λx

− e

−λ(x

+∆

)

¢¡

−λx

− e

−λ(x

+∆

)

= P{ζ

∈ [x

, x

+ ∆

)}P{ζ

∈ [x

, x

+ ∆

)}.

По индукции аналогично можно доказывать независимость событий

{ζ

∈ [x

, x

+ ∆

)} и {ζ

∈ [x

, x

+ ∆

), j = 2, . . . , k + 1}

при всех k > 2.

Следствие 6.2. Если ν(t) — однородный пуассоновский процесс с

интенсивностью λ, {τ

}

k∈Z

— последовательные моменты его скачков и τ

(t), τ

−

(t)

— те же случайные величины, что в Утверждении 3, то при любом t ∈ (0, ∞)

M(τ

k+1

− τ

) = Mτ

(t) = Mτ

−

(t) = 1/λ,

M(τ

κ+1

− τ

|κ = max{n : τ

< t}) =

Первая цепочка равенств следует из Утверждения 6.3 и Следствия 6.1, а вторая

— из того, что

M{τ

κ+1

− τ

|κ = max{n : τ

< t}} = M{τ

(t) + τ

−

(t)}.

Пример 6.1. Следствие 6.2 называют «парадоксом времени ожидания»: если

моменты прибытия автобусов на остановку образуют пуассоновский поток с

параметром λ, а t — момент прихода пассажира на остановку, то среднее время

ожидания пассажиром ближайшего автобуса равно среднему промежутку между

моментами прибытия соседних автобусов.

Как и многие другие парадоксы, парадокс времени ожидания возникает в

результате отождествления разных понятий. Пусть . . . , τ

−1

, τ

, . . . — моменты

прибытия автобусов. Когда говорят о среднем промежутке между моментами

прибытия соседних автобусов, то имеют в виду среднее значение разности τ

−

k−1

, вычисляемое по моментам τ

, а когда говорят о среднем времени ожидания

ближайшего автобуса, то имеют в виду среднее время ожидания, вычисляемое

для случайной точки на оси времени. Но короткие промежутки между моментами

прибытия автобусов занимают на оси времени относительно меньшее место, чем

длинные, поэтому «случайная» точка с б´ольшей вероятностью попадает на более

длинные интервалы, и среднее время ожидания оказывается больше половины

среднего промежутка между моментами прибытия соседних автобусов (кроме

вырожденной ситуации, когда промежутки между моментами прибытия автобусов

не случайны и одинаковы). Например, автобусов приходится долго ждать, если они

приходят по 4 машины подряд.

Пример 6.2 ([3], т. 2, гл. VI, §7). Пусть в устройстве работает большое число

одинаковых приборов (например, реле), которые заменяются по мере выхода из

строя, и моменты замены отмечаются в журнале. Чтобы оценить средний срок

службы прибора, контролер выбрал какой-то день X в достаточно далеком прошлом

(так что все приборы, работавшие в этот момент, уже заменены), по журналу

вычислил сроки службы всех приборов, работавших в день X, и выбрал в качестве

статистической оценки среднего срока службы прибора среднее арифметическое

этих времен. Если срок службы прибора имеет показательное распределение,

то математическое ожидание построенной таким образом оценки вдвое больше

истинного математического ожидания срока службы!

Этот пример косвенно показывает, что оценки «средней длительности жизни» в

конкретной стране в конкретный момент времени не могут быть точными и зависят

от методики их построения.

Утверждение 6.4. При условии, что на отрезке [a, b] происходит ровно n

скачков пуассоновского процесса с интенсивностью λ, совместное распределение

значений ζ

< . . . < ζ

моментов этих скачков совпадает с распределением

вариационного ряда ξ

(1)

< . . . < ξ

(n)

, построенного по независимым случайным

величинам ξ

, . . . , ξ

, равномерно распределенным на отрезке [a, b].

Доказательство. Плотность совместного распределения ξ

(1)

, . . . , ξ

(n)

найти

несложно: при любом наборе x = {a < x

< x

< . . . < x

< b} и любом наборе

δ = (δ

, . . . , δ

∈ (0, min{x

− x

, x

− x

, . . . , x

− x

n−1

})

событию A(x, δ) = {ξ

(j)

∈ (x

, x

+ δ

), j = 1, . . . , n} соответствует n!

непересекающихся событий

(x, δ) = {ξ

∈ (x

, x

+ δ

), j = 1, . . . , n}, σ = (σ

, . . . , σ

) ∈ S

где S

— множество всех n! перестановок чисел 1, . . . , n. Вероятность каждого

события A

(x, δ) равна

...δ

(b−a)

, поэтому плотность совместного распределения

(1)

, . . . , ξ

(n)

есть

lim

,...,δ

↓0

A(x, δ)

. . . δ

(

(b−a)

, если a < x

< x

< . . . < x

< b,

0 в остальных случаях.

С другой стороны, согласно свойствам пуассоновского процесса при δ

, . . . , δ

↓ 0

(полагая для удобства x

+ δ

= a, x

n+1

= b) имеем

P{ζ

∈ (x

, x

+ δ

), j = 1, . . . , n, ν(b) − ν(a) = n} =

= P{ν(x

j+1

) − ν(x

+ δ

) = 0 (j = 0 , . . . , n), ν(x

+ δ

) − ν(x

) = 1 (j = 1 , . . . , n)} =

n+1

j=1

−λ(x

−x

j−1

−δ

j−1

)

j=1

λδ

(1 + o(1)) = e

−λ(b−a−δ

−...−δ

)

. . . δ

(1 + o(1)),

P{ν(b) − ν(a) = n} =

(λ(b − a))

−λ(b−a)

Значит, при a < x

< . . . < x

< b

lim

,...,δ

↓0

P{ζ

∈ (x

, x

+ δ

), j = 1, . . . , n |ν(b) − ν(a) = n}

. . . δ

= lim

,...,δ

↓0

−λ(b−a−δ

−...−δ

)

. . . δ

(1 + o(1))

(λ(b−a))

−

(

−

)

(b − a)

что совпадает с плотностью совместного распределения ξ

(1)

, . . . , ξ

(n)

. Утверждение

доказано.

Рассмотрим примеры применения пуассоновских процессов в теории массового

обслуживания.

Пример 6.3 (число заявок на периоде занятости). Рассмотрим простейшую

модель системы массового обслуживания (кассир в магазине, ремонтное устройство

и т.п.). Пусть в систему, состоящую из одного обслуживающего прибора, приходят

заявки, моменты поступления которых образуют однородный пуассоновский поток

с интенсивностью λ; n-я заявка обслуживается прибором случайное время γ

которое не зависит от времен обслуживания остальных заявок и имеет функцию

распределения G(x). Заявки, во время прихода которых прибор обслуживает другие

заявки, образуют очередь. Если очередь не пуста, то обслуживающий прибор,

завершив обслуживание заявки, сразу же начинает обслуживание следующей.

Говорят, что такая система имеет тип M|G|1.

Работа системы массового обслуживания типа M|G|1 состоит из

последовательности чередующихся периодов занятости обслуживающего прибора

(непрерывного обслуживания заявок) и периодов простоя (ожидания прихода

заявки после окончаний периода занятости). Периоды простоя независимы и

имеют такое же распределение, как случайная величина τ

(t), т. е. показательное

распределение с параметром λ. Период занятости может оказаться и бесконечным:

если прибор не будет успевать обслуживать приходящие заявки, то очередь будет

расти неограниченно.

Теорема 6.5. Период занятости в системе M|G|1 конечен с вероятностью 1

тогда и только тогда, когда λMγ

≤ 1.

Доказательство. Введем вспомогательный ветвящийся процесс Гальтона–

Ватсона; будем считать заявку, с которой начинается период занятости, частицей

нулевого поколения. Пока заявка обслуживается, в систему могут поступать новые

заявки; будем их считать частицами-потомками начальной частицы, образующими

первое поколение. Заявки, приходящие за время обслуживания каждой «частицы»

первого поколения, будем считать ее потомками; таким образом, заявки, пришедшие

за время обслуживания частиц первого поколения, образуют второе поколение, и

т. д. Период занятости конечен тогда и только тогда, когда этот процесс на каком-то

поколении вырождается.

Найдем распределение числа заявок в однородном пуассоновском потоке,

приходящих за время обслуживания одной заявки. Вероятность того, что за время

t произойдет k событий однородного пуассоновского потока с интенсивностью λ,

равна

(λt)

−t

, k = 0, 1, . . .. По формуле полной вероятности по времени обслуживания

заявки вероятность того, что за это время придет k новых заявок, есть

∞

(λt)

−t

dG(t), k = 0, 1, . . . ,

и математическое ожидание числа «потомков» заявки равно поэтому

∞

k=0

∞

k=0

∞

(λt)

−t

dG(t) =

∞

k=0

(λt)

−t

dG(t) =

∞

λtdG(t) = λMγ

Покажем, что построенный процесс действительно является ветвящимся

процессом Гальтона–Ватсона; для этого осталось проверить, что числа потомков

разных частиц независимы. Для любого натурального k < ∞ при любых

фиксированных длительностях обслуживания первых k заявок и любых числах

заявок, поступавших за времена обслуживания первых k заявок, время

обслуживания (k + 1)-й заявки имеет функцию распределения G(t), а число заявок,

приходящих за время ее обслуживания — распределение {r

}. Следовательно,

числа потомков разных частиц независимы и одинаково распределены, и процесс

размножения «частиц-заявок» — ветвящийся процесс.

Ветвящийся процесс вырождается с вероятностью 1 тогда и только тогда, когда

среднее число потомков одной частицы, равное λMγ

, не превышает 1; тем самым

теорема доказана.

Смысл условия теоремы состоит в том, что среднее число заявок, приходящих за

время обслуживания одной заявки, не должно быть больше 1.

Такое соответствие между процессами массового обслуживания и ветвящимися

процессами позволяет получать и более детальную информацию о свойствах периода

занятости, например, о суммарном числе требований, обслуженных на одном периоде

занятости.

Теорема 6.6. Для системы массового обслуживания M|G|1 из теоремы 6.5

математическое ожидание числа заявок, обслуженных на периоде занятости,

равно

1−λMγ

, если λMγ

< 1.

Доказательство. Рассмотрим ту же интерпретацию заявок, приходящих на

периоде занятости, как частиц, образующих ветвящийся процесс Гальтона–Ватсона.