Зубков А.М. Конспект лекций по теории случайных процессов
Подождите немного. Документ загружается.

условное математическое ожидание ξ относительно разбиения B как функцию,
отображающую Ω в R (т.е. как случайную величину):
M{ξ|B}(ω) =
X
k≥1
x
k
P{A
k
|B}(ω) =
X
k≥1
x
k
P{ξ = x
k
|B}(ω).
Преобразуем эту формулу:
M{ξ|B}(ω) =
X
k≥1
x
k
P{A
k
|B}(ω) =
X
k≥1
x
k
X
j≥1
P{A
k
|B
j
}χ
B
j
(ω) =
=
X
j≥1
χ
B
j
(ω)
X
k≥1
x
k
P{A
k
|B
j
} =
X
j≥1
χ
B
j
(ω)M{ξ|B
j
}.
Таким образом, условное математическое ожидание ξ относительно разбиения B
есть случайная величина, принимающая на каждом элементе
B
j
этого разбиения
постоянное значение, равное M{ξ|B
j
} ∈ R. Значит, M{ξ|B}(ω) — функция,
измеримая относительно разбиения B (для любого B-измеримого множества D
событие {ω : M{ξ|B} ∈ D} является объединением множеств B
j
, т.е. принадлежит
σ-алгебре, порожденной разбиением B).
Утверждение 8.1. Для любой случайной величины ξ и для любого события C,
измеримого относительно разбиения B = {B
1
, B
2
, . . .}, справедлива формула
Mχ
C
ξ = M{χ
C
M{ξ|B}}. (37)
Доказательство. Действительно, так как C измеримо относительно B, то C =
S
j:B
j
⊂C
B
j
и
Mχ
C
ξ =
X
ω∈C
ξ(ω)P{ω} =
X
j:B
j
⊂C
X
ω∈B
j
ξ(ω)P{ω} =
=
X
j:B
j
⊂C
X
ω∈B
j
ξ(ω)P{ω|B
j
}P{B
j
} =
X
j:B
j
⊂C
M{ξ|B
j
}P{B
j
} =
=
X
j:B
j
⊂C
M{ξ|B
j
}
X
ω∈B
j
P{ω} =
X
ω∈C
M{ξ|B}(ω)P{ω} = Mχ
C
M{ξ|B}.
Следствие 8.1. Для любой случайной величины ξ и любого разбиения B
справедлива формула полного математического ожидания:
Mξ = MM{ξ|B}.
В рассмотренном нами случае конечных разбиений определения условных
распределений и математических ожиданий конструктивны и довольно наглядны. В
общем случае, когда разбиения B порождаются, например, величинами, имеющими
непрерывные распределения, условное математическое ожидание относительно σ-
алгебры B определяется неконструктивно с помощью аналога формулы (43).
51
Условным математическим ожиданием случайной величины ξ относительно σ-
алгебры B называется случайная величина M{ξ|B}, измеримая относительно B и
удовлетворяющая тождеству
Z
C
ξdP =
Z
C
M{ξ|B}dP для любого события C ∈ B. (38)
Доказательство существования такой случайной величины нетривиально и
основывается на теореме Радона–Никодима:
Теорема Радона–Никодима. Пусть (Ω, F) — измеримое пространство, P —
σ-конечная мера на F и λ — абсолютно непрерывная относительно P мера со
знаком (т.е. λ = λ
1
−λ
2
, где меры λ
1
и λ
2
неотрицательны и хотя бы одна из них
конечна). Тогда существует такая F-измеримая функция f = f(ω): Ω → [−∞, ∞],
что
λ(B) =
Z
C
f(ω)P (dω), C ∈ F. (39)
С точностью до множества P -меры нуль функция f единственна: если h — другая
функция, удовлетворяющая (44), то P {ω: f(ω) 6= h(ω)} = 0.
В нашем случае мера λ(C) =
R
C
ξdP, C ∈ B, а f(ω) = M{ξ|B} — плотность меры
λ относительно меры P. Теорема Радона–Никодима относится к теории меры; ее
доказательство можно найти, например, в учебнике А.А.Боровкова [1].
Отметим свойства условных математических ожиданий, которые нам
потребуются в дальнейшем.
1) Линейность: для любых случайных величин ξ, η с конечными математическими
ожиданиями и чисел a, b справедливо равенство
M{aξ + bη|B} = aM{ξ|B} + bM{η|B}.
2) Если существует Mξ, то M{ξ|{∅, Ω}} = Mξ.
3) P{ξ = C = const} = 1 ⇒ M{ξ|B} = C.
4) M{χ
A
|B} = P{A|B} для любого A ∈ F.
Пусть B порождается разбиением {B
1
, B
2
, . . .}, тогда в силу свойства 1)
M{χ
A
|B} = M
(
X
i≥1
χ
AB
i
|B
)
=
=
X
i≥1
M{χ
AB
i
|B
i
}χ
B
i
(ω) =
X
i≥1
P{A|B
i
}χ
B
i
(ω) = P{A|B}.
5) Если A = {A
1
, A
2
, . . .} — разбиение, порожденное случайной величиной ξ, то
M{ξ|A} = ξ.
Действительно, P{ξ = x
k
|A
k
} = 1 для каждого k ≥ 1.
6) Пусть B
1
и B
2
— два разбиения. Если из C ∈ B
1
следует,что C ∈ B
2
, то будем
говорить, что разбиение B
1
содержится в разбиении B
2
, и записывать это так: B
1
⊂
52
B
2
; иначе говоря, запись B
1
⊂ B
2
означает, что B
2
— разбиение на более мелкие
подмножества. Тогда
M{M{ξ|B
2
}|B
1
} = M{ξ|B
1
}. (40)
Доказательство. По определению (45) эквивалентно тому, что
M{M{ξ|B
2
}|C} = M{ξ|C} для каждого C ∈ B
1
. (41)
Из условия B
1
⊂ B
2
следует, что ограничение разбиения B
2
на множество C образует
разбиение множества C. Значит, (47) является формулой полного математического
ожидания, примененной к условному распределению ξ на множестве C.
7) Если случайная величина η измерима относительно разбиения B =
{B
1
, B
2
, . . .}, то
M{ξη|B} = ηM{ξ|B},
т.е. из-под знака условного математического ожидания можно выносить
случайный множитель, измеримый относительно σ-алгебры в условии.
Доказательство. Будем считать, что η принимает на множестве B
j
значение
b
j
, j ≥ 1. По определению
M{ξη|B}(ω) =
X
j≥1
χ
B
j
(ω)M{ξη|B
j
} =
X
j≥1
χ
B
j
(ω)M{ξb
j
|B
j
} =
=
X
j≥1
b
j
χ
B
j
(ω)M{ξ|B
j
} =
X
j≥1
ηM{ξ|B
j
}χ
B
j
(ω),
т.е. M{ξη|B} — это случайная величина, которая на B
j
равна ηM{ξ|B
j
} при любом
j ≥ 1. Значит, она равна ηM{ξ|B}.
9. Мартингалы
Случайные процессы, которые называются мартингалами, возникли как
математическая модель, предназначенная для поиска оптимальной стратегии выбора
ставок участником случайной игры (в казино, на бирже, при вложении капитала в
производство и т.п.). Наряду с такими практическими применениями оказалось, что
мартингалы могут применяться и при решении чисто математических задач. Этот
класс определяется условиями, выраженными в терминах условных математических
ожиданий. Мы будем рассматривать последовательности случайных величин,
являющиеся мартингалами, т.е. мартингалы с дискретным временем.
Определение. Пусть (Ω, F, P) — вероятностное пространство, на котором
заданы последовательность случайных величин X
0
, X
1
, . . . и расширяющаяся
последовательность (поток) σ-алгебр F
0
⊂ F
1
⊂ F
2
⊂ . . . ⊂ F (каждая следующая σ-
алгебра получается разбиением предыдущей). Последовательность пар (X
n
, F
n
, n =
0, 1, . . .) называется мартингалом (или X
n
— мартингал относительно {F
n
}), если
а) M|X
n
| < ∞ для всех n = 0, 1, . . . ,
б) X
n
измерима относительно F
n
, n = 0, 1, . . . ,
в) P{M{X
m
|F
n
} = X
n
} = 1 при любых m > n, m, n ∈ {0, 1, . . .}.
53

Последовательность пар (X
n
, F
n
, n = 0, 1, . . .) называется субмартингалом, если
для нее выполнены условия а), б) и
в
0
) P{M{X
m
|F
n
} ≥ X
n
} = 1 при любых m > n, m, n ∈ {0, 1, . . .},
и супермартингалом, если она удовлетворяет условиям а), б) и
в
00
) P{M{X
m
|F
n
} ≤ X
n
} = 1 при любых m > n, m, n ∈ {0, 1, . . .}.
Условие в
0
) означает, что X
n
ограничивает значения M{X
m
|F
n
} при m > n снизу,
а условие в
00
) — что X
n
ограничивает значения M{X
m
|F
n
} при m > n сверху; этим
объясняются приставки «суб-» и «супер-».
Изменение знака переводит субмартингал в супермартингал и обратно,
поэтому часто их называют полумартингалами. Теоремам, доказанным для
супермартингалов, соответствуют эквивалентные теоремы для субмартингалов.
Условие в) (и аналогично условия в
0
), в
00
)) записывают также в виде
M{X
m
|F
n
} = X
n
п.н. (почти наверное); в теории вероятностей случайные величины,
различающиеся на множестве меры 0, считаются эквивалентными.
В силу условия б) и того, что последовательность σ-алгебр {F
n
} расширяющаяся,
σ-алгебра σ(X
0
, . . . , X
n
), порожденная случайными величинами X
0
, . . . , X
n
,
содержится в F
n
при любом n.
Соотношение в) эквивалентно своему частному случаю:
M{X
n+1
|F
n
} = X
n
при любом n. (42)
Действительно, если выполнено (42), то при m > n + 1 из него и свойства 6)
условных математических ожиданий следует свойство в):
M{X
m
|F
n
} = M{M{X
m
|F
m−1
}|F
n
} =
M{X
m−1
|F
n
} = . . . = M{X
n+1
|F
n
} = X
n
.
Аналогичные эквивалентные формы имеют условия в
0
) и в
00
).
Из условия в), из того, что σ(X
n
) ⊂ F
n
, и из свойств условного математического
ожидания следует, что
M{X
n+1
|σ(X
n
)} = M{M{X
n+1
|F
n
}|σ(X
n
)} = M{X
n
|σ(X
n
)} = X
n
, (43)
т.е. условное математическое ожидание значения мартингала в момент времени n+ 1
относительно σ-алгебры, порожденной X
n
, равно его значению в момент n; иными
словами, мартингал — это процесс без сноса (в том смысле, что его математическое
ожидание в следующий момент времени совпадает со значением в текущий момент).
Условие (43) следует из (42), но (42) не следует из (43), так как, вообще говоря,
σ(X
n
) 6= σ(X
1
, . . . , X
n
) ⊂ F
n
.
Пример 9.1. Пусть Z
1
, Z
2
и Z
3
принимают значения −1, 0 и 1, причем Z
1
и Z
2
независимы и одинаково распределены:
P{Z
k
= −1} = P{Z
k
= 0} = P{Z
k
= 1} =
1
3
, k = 1, 2,
а Z
3
≡ Z
2
− Z
1
(mod 3). Положим
X
1
= Z
1
, X
2
= Z
1
+ Z
2
, X
3
= Z
1
+ Z
2
+ Z
3
.
54
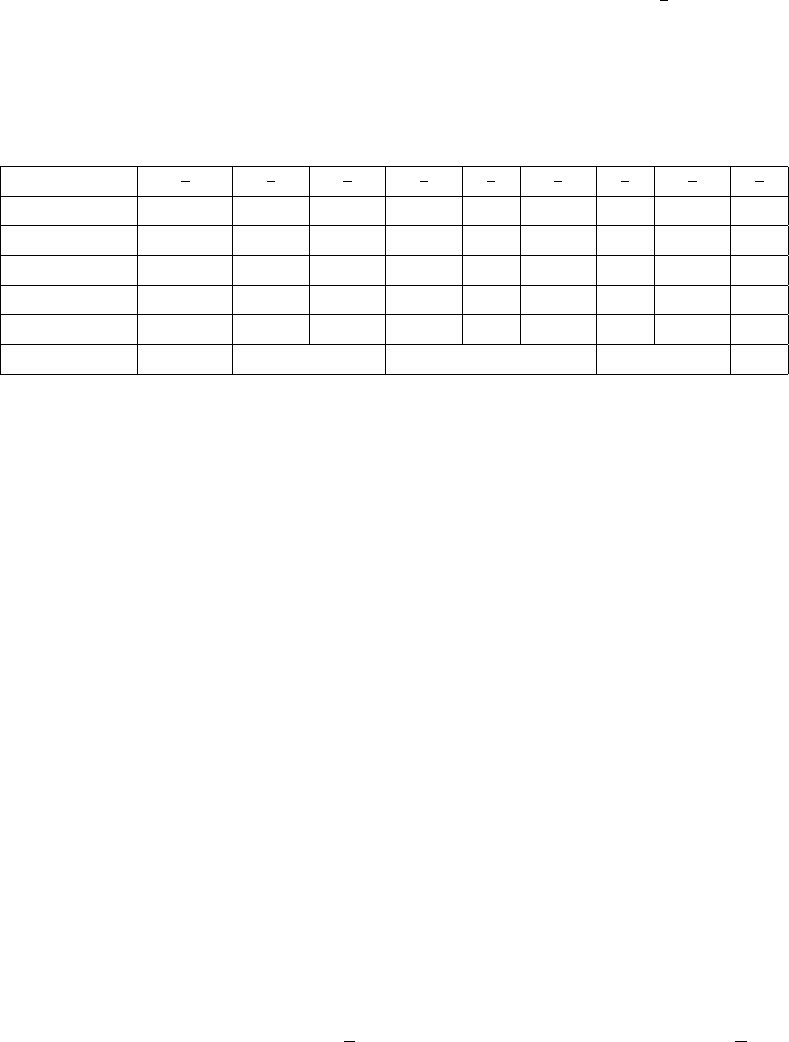
Так как случайные величины Z
1
и Z
2
принимают по три значения каждая
и определяют все остальные случайные величины, то в качестве пространства
элементарных событий можно выбрать пространство из 9 точек, соответствующих
разным значениям пары (Z
1
, Z
2
) и имеющих вероятности, равные
1
9
. Функции
Z
3
= Z
3
(Z
1
, Z
2
) = Z
2
− Z
1
(mod 3), X
1
= X
1
(Z
1
, Z
2
) = Z
1
,
X
2
= X
2
(Z
1
, Z
2
) = Z
1
+ Z
2
, X
3
= X
3
(Z
1
, Z
2
) = Z
1
+ Z
2
+ Z
3
можно задать таблицей
p
1
9
1
9
1
9
1
9
1
9
1
9
1
9
1
9
1
9
Z
1
, Z
2
−1, −1 −1, 0 0, −1 −1, 1 0, 0 1, −1 0, 1 1, 0 1, 1
Z
3
0 1 −1 −1 0 1 1 −1 0
X
1
−1 −1 0 −1 0 1 0 1 1
X
2
−2 −1 −1 0 0 0 1 1 2
X
3
−2 0 −2 −1 0 1 2 0 2
M{X
3
|X
2
} −2 ( 0–2)/2=–1 ( –1+0+1)/3=0 (2+0)/2=1 2
В строке X
2
разными шрифтами выделены множества {X
2
= k}, образующие
σ-алгебру σ(X
2
). Из таблицы видно, что значения X
1
и X
2
полностью определяют
Z
1
и Z
2
и что
M{X
3
|X
1
, X
2
} = X
3
6= X
2
, но M{X
3
|X
2
} = X
2
.
Приведем несколько примеров случайных процессов, являющихся мартингалами
или не являющихся ими.
Примеры. 9.2. Пусть ξ
1
, ξ
2
, . . . — независимые случайные величины и X
n
= ξ
1
+
. . . + ξ
n
, n = 1, 2, . . . Если Mξ
n
= 0 при всех n, то случайный процесс X
n
является
мартингалом, если Mξ
n
≥ 0 при всех n — то субмартингалом, если Mξ
n
≤ 0 при всех
n — то супермартингалом.
9.3. При условиях примера 9.2 последовательность X
0
= 1, X
n
= ξ
1
. . . ξ
n
при
n = 1, 2, . . . — мартингал, если Mξ
n
= 1 при всех n ≥ 1.
Задача 9.1. Является ли эта последовательность субмартингалом, если Mξ
n
> 1
при всех n?
9.4. При условиях примера 9.1 последовательность X
n
= ξ
1
ξ
2
+ ξ
2
ξ
3
+ . . . + ξ
n
ξ
n+1
— мартингал, если Mξ
n
= 0 при всех n ≥ 1.
Если выполнено более слабое условие: Mξ
2n
= 0 при всех n ≥ 1, то Mξ
k
ξ
k+1
= 0
при всех k ≥ 0, но последовательность X
n
может и не быть мартингалом. Например,
пусть при n = 0, 1, . . .
P{ξ
2n
= 1} = P{ξ
2n
= −1} =
1
2
, P{ξ
2n+1
= 1} = P{ξ
2n+1
= 3} =
1
2
;
тогда
M{X
2
|X
1
= 3} = M{ξ
1
ξ
2
+ ξ
2
ξ
3
|ξ
1
= 3, ξ
2
= 1} = 3 + Mξ
3
= 5 6= X
1
.
9.5. Пусть на вероятностном пространстве (Ω, F, P ) заданы расширяющаяся по-
следовательность σ-алгебр F
0
⊂ F
1
⊂ . . . и случайная величина ξ, M|ξ| < ∞.
55
Определим случайный процесс {X
n
} формулой X
n
= M{ξ|F
n
}, n = 0, 1, . . .
Наглядный смысл случайного процесса {X
n
} простой: это значения условных
математических ожиданий ξ относительно измельчающихся разбиений пространства
элементарных событий Ω.
Покажем, что X
n
— мартингал. Если m > n, то по определению X
n
и по свойствам
условного математического ожидания
M{X
m
|F
n
} = M{M{ξ|F
m
}|F
n
} = M{ξ|F
n
} = X
n
.
Случайный процесс {X
n
} — это мартингал, порожденный случайной величиной ξ. В
известном смысле это общий вид сходящегося мартингала: если мартингал {X
n
} при
n → ∞ сходится с вероятностью 1 к интегрируемой (т.е. имеющей математическое
ожидание) случайной величине X так, что M|X
n
− X| → 0, то
X
n
= lim
m→∞
M{X
m
|F
n
} = M{X|F
n
}.
Задача 9.2. Пусть X
1
, X
2
, . . . — последовательность случайных величин,
принимающих значения из конечного множества, например, из множества
{0, 1, . . . , N}. Показать, что если (X
n
, σ(X
1
, . . . , X
n
)) — мартингал, то состояния 0
и N — поглощающие, т.е. что
P{X
k+1
= 0|X
k
= 0} = P{X
k+1
= N|X
k
= N} = 1.
9.1. Связь субмартингалов и мартингалов. Разложение Дуба
Определение. Пусть {F
n
}
n>0
— расширяющаяся последовательность σ-
алгебр. Последовательность случайных величин {ξ
n
} называется предсказуемой
относительно {F
n
}, если ξ
n
измерима относительно F
n−1
при любом n ≥ 1.
Например, если ζ
1
(ω), ζ
2
(ω), . . . — последовательность случайных величин,
заданных на вероятностном пространстве (Ω, F, P), которая порождает σ-алгебры
F
n
= σ(ζ
1
, . . . , ζ
n
), n = 1, 2, . . ., а последовательность случайных величин {ξ
n
(ω)}
предсказуема относительно {F
n
}, то существует такая последовательность неслу-
чайных функций f
n
(·), что ξ
n
(ω) = f
n
(ζ
1
(ω), . . . , ζ
n−1
(ω)) при P-почти всех ω ∈ Ω.
Теорема 9.1 (Разложение Дуба). Пусть (X
n
, F
n
) — субмартингал.
Существуют такие мартингал (Z
n
, F
n
) и предсказуемая относительно {F
n
}
неубывающая с вероятностью 1 последовательность случайных величин
{A
n
}, A
0
= 0, что P{X
n
= Z
n
+ A
n
} = 1 при каждом n ≥ 0. С точностью
до множества меры 0 процессы {Z
n
} и {A
n
} определяются однозначно.
Доказательство. Так как A
0
= 0, то Z
0
= X
0
определяется однозначно. Далее,
имея в виду тождество
X
n
= X
0
+
n−1
X
j=0
(X
j+1
− X
j
) =
= X
0
+
n−1
X
j=0
{[X
j+1
− M{X
j+1
|F
j
}] + [M{X
j+1
|F
j
} − X
j
]},
56
определим искомые случайные величины равенствами
Z
n
= Z
0
+
n−1
X
j=0
[X
j+1
− M{X
j+1
|F
j
}] = Z
n−1
+ [X
n
− M{X
n
|F
n−1
}],
A
n
=
n−1
X
j=0
[M{X
j+1
|F
j
} − X
j
].
Так как (X
n
, F
n
) — субмартингал, то все слагаемые, составляющие A
n
,
неотрицательны, значит, каждая реализация {A
n
} не убывает. Из свойств условного
математического ожидания и из того, что F
1
⊂ F
2
⊂ . . ., следуют соотношения
A
n
∈ F
n−1
, Z
n
∈ F
n
и
M{Z
n
|F
n−1
} = Z
n−1
+ M{X
n
− M{X
n
|F
n−1
}|F
n−1
} = Z
n−1
при всех n ≥ 1,
т. е. (Z
n
, F
n
) — мартингал.
Для доказательства единственности представления X
n
= Z
n
+ A
n
допустим,
что P{X
n
= Z
∗
n
+ A
∗
n
} = 1 при каждом n ≥ 0, где (Z
∗
n
, F
n
) - мартингал, {A
∗
n
} -
неубывающая случайная последовательность, A
∗
0
= 0, A
∗
n
∈ F
n−1
при всех n ≥ 1.
Приравнивая два представления для разности X
n+1
− X
n
, получаем, что для почти
всех ω ∈ Ω
(Z
n+1
− Z
n
) + (A
n+1
− A
n
) = X
n+1
− X
n
= (Z
∗
n+1
− Z
∗
n
) + (A
∗
n+1
− A
∗
n
).
Теперь вычислим условные математические ожидания относительно F
n
от крайних
частей: p{A
n+1
− A
n
= A
∗
n+1
− A
∗
n
} = 1 при всех n ≥ 0. Отсюда и из условия A
0
=
A
∗
0
= 0 по индукции следует, что p{A
n
= A
∗
n
, Z
n
= Z
∗
n
} = 1 при всех n.
Лемма 9.1. Если (X
n
, F
n
) — мартингал и g(x) — выпуклая функция, причем
M|g(X
n
)| < ∞ при всех n ≥ 0, то (g(X
n
), F
n
) — субмартингал.
Если g(x), кроме того, монотонно возрастает и (X
n
, F
n
) — субмартингал, то
(g(x), F
n
) — субмартингал.
Доказательство. Достаточно доказать, что с вероятностью 1
M{g(X
n+1
)|F
n
}(ω) ≥ g(X
n
(ω)). (44)
Функция g(x) выпукла; поэтому существует такая неубывающая функция g
∗
(x), что
g(y) ≥ g(x) + g
∗
(x)(y −x) для любых x, y, принадлежащих области определения g(x).
Из этого неравенства и из свойств условных математических ожиданий следует, что
M{g(X
n+1
)|F
n
} ≥ M{g(X
n
) + g
∗
(X
n
)(X
n+1
− X
n
)|F
n
} =
= M{g(X
n
)|F
n
} + M{g
∗
(X
n
)(X
n+1
− X
n
)|F
n
}.
Случайная величина X
n
измерима относительно F
n
; поэтому g(X
n
) и g
∗
(X
n
) тоже
измеримы относительно F
n
и
M{g(X
n
)|F
n
} = g(X
n
),
M{g
∗
(X
n
)(X
n+1
− X
n
)|F
n
} = g
∗
(X
n
)M{X
n+1
− X
n
|F
n
} = 0,
57
т.е. M{g(X
n
)|F
n
} ≥ g(X
n
).
Второе утверждение леммы доказывается точно так же, только в последнем
равенстве нужно учесть, что g
∗
(x) ≥ 0 и (в соответствии с определением
субмартингала) M{X
n+1
− X
n
|F
n
} ≥ 0.
9.2. Моменты остановки
Определение. Пусть на вероятностном пространстве (Ω, F, P) задан поток σ-
алгебр F
0
⊂ F
1
⊂ . . . Случайную величину ν будем называть моментом остановки
относительно потока {F
n
}, если {ω : ν ≤ n} ∈ F
n
для каждого n ≥ 0.
Такую случайную величину называют также марковским моментом или случайной
величиной, не зависящей от будущего.
Пример 9.6. Если {X
n
} — такая последовательность случайных величин, что X
n
измерима относительно F
n
при n = 1, 2, . . ., а B
n
— последовательность измеримых
множеств, то ν = min{n : X
n
∈ B
n
} — момент остановки. Например, если f(n) —
неслучайная функция и B
n
= {ω: X
n
> f(n)}, то ν = min{n: X
n
> f(n)} — момент
первого выхода траектории {X
n
} из области {(n, x) : x ≤ f(n)} — является моментом
остановки.
Простые свойства. а) Если ν — момент остановки, m = const, то ν
∗
= min{ν, m}
— тоже момент остановки. Действительно, если n ≥ m, то {ν
∗
≤ n} = Ω ∈ F
n
, а если
n < m, то {ν
∗
≤ n} = {ν ≤ n} ∈ F
n
.
б) Если ν — момент остановки, то
{ν = n} = {ν ≤ n}\{ν ≤ n − 1} ∈ F
n
,
{ν ≥ n} = {ν > n − 1} = Ω\{ν ≤ n − 1} ∈ F
n−1
.
Обратно, если {ν = n} ∈ F
n
при каждом n, то {ν ≤ n} ∈ F
n
, т.е. ν — момент
остановки.
Пусть ν — момент остановки относительно расширяющегося семейства σ-алгебр
F
0
⊂ F
1
⊂ . . . ⊂ F, {ν = ∞} = ∅ и (X
n
, F
n
) — мартингал или субмартингал. Тогда
можно определить случайную величину
X
ν
=
X
n≥0
X
n
χ{ν = n}
— значение мартингала (субмартингала) в случайный момент ν. В математической
модели азартной игры момент остановки может соответствовать моменту выхода
игрока из игры, и тогда X
ν
— его итоговый капитал.
Лемма 9.2. Если (X
n
, F
n
) — мартингал (субмартингал) и ν — момент
остановки относительно {F
n
}, то остановленная последовательность
(X
min{n,ν}
, F
n
) тоже образует мартингал (субмартингал).
Доказательство. Воспользуемся равенствами
X
min{n,ν}
=
n
X
m=0
X
m
χ{ν = m} + X
n
χ{ν > n}
58
и
X
min{n+1,ν}
=
n+1
X
m=0
X
m
χ{ν = m} + X
n+1
χ{ν > n + 1} =
=
n
X
m=0
X
m
χ{ν = m} + X
n+1
χ{ν > n}.
Из первого равенства следует, что случайная величина X
min{n,ν}
измерима
относительно F
n
и интегрируема, а из обоих равенств — что
X
min{n+1,ν}
− X
min{n,ν}
= χ{ν > n}(X
n+1
− X
n
).
Так как χ{ν > n} ∈ F
n
, то по свойствам условных математических ожиданий
M{X
min{n+1,ν}
− X
min{n,ν}
|F
n
} = M{χ{ν > n}(X
n+1
− X
n
)|F
n
} =
= χ{ν > n}M{X
n+1
− X
n
|F
n
},
и правая часть равна 0, если X
n
— мартингал, и неотрицательна, если X
n
—
полумартингал.
9.3. Сохранение свойства мартингала для случайных моментов
остановки
Если {X
n
, F
n
} — мартингал, то MX
n
= MX
0
. А что можно сказать о значении
MX
ν
, если ν — случайная величина? Если ν — момент остановки, то согласно
лемме 9.2 последовательность {X
min{n,ν}
, F
n
} — мартингал, т.е. MX
min{n,ν}
= MX
0
.
Хотя min{ν, n} ↑ ν, n ↑ ∞, переходить к предельному равенству MX
ν
= MX
0
(как при предельном переходе под знаком интеграла) можно только при некоторых
дополнительных условиях.
Например, пусть {ξ
n
} — независимые одинаково распределенные случайные
величины, имеющие стандартное нормальное распределение, X
n
= ξ
1
+ . . . + ξ
n
— симметричное случайное блуждание (которое является мартингалом, так как
Mξ
k
= 0 при всех k), а момент остановки ν = min{n : X
n
< 0}. В силу
закона повторного логарифма последовательность {X
n
} с вероятностью 1 бесконечно
много раз меняет знак, поэтому P{ν < ∞} = 1, значение X
ν
с вероятностью 1
отрицательно, значит, 0 > MX
ν
6= MX
0
= 0.
Следующая теорема указывает условия, при которых MX
ν
= MX
0
.
Теорема 9.2 (сохранение мартингальности для момента остановки). Пусть
{X
n
, F
n
} — мартингал на вероятностном пространстве (Ω, F, P) и ν — такой
момент остановки относительно потока σ-алгебр {F
n
}, что
M|X
ν
| < ∞, lim inf
n→∞
M|X
n
|χ{ν > n} = 0. (45)
Тогда для P-почти всех ω ∈ Ω
M{X
ν
|F
0
}(ω) = X
0
(ω). (46)
59
Если те же условия выполнены для субмартингала {X
n
, F
n
}, то для P-почти всех
ω ∈ Ω
M{X
ν
|F
0
}(ω) ≥ X
0
(ω).
Доказательство. Пусть {X
n
, F
n
} — мартингал. Нам нужно доказать, что
случайные величины M{X
ν
|F
0
} и X
0
(т. е. измеримые функции, заданные на
пространстве элементарных исходов) совпадают P-почти наверное. Сначала сведем
эту задачу к эквивалентной, но проще решаемой.
Если f и g — две F-измеримые функции на Ω и P{f 6= g} > 0, то либо
P{f > g} > 0, либо P{f < g} > 0. Если, например, P{f > g} > 0, то существует
F-измеримое множество, интеграл по которому от f больше интеграла от g:
Z
ω:f(ω)>g(ω)
fP(dω) >
Z
ω:f(ω)>g(ω)
gP(dω).
Значит, если интегралы от измеримых функций f и g по всем измеримым
множествам совпадают, то P{f 6= g} = 0. Полагая здесь
f(ω) = M{X
ν
|F
0
}(ω) и g(ω) = X
0
(ω),
получаем, что утверждение теоремы является следствием соотношения
M{M{X
ν
|F
0
}χ{A}} = MX
0
χ{A} для всех A ∈ F
0
. (47)
Пользуясь свойствами условных математических ожиданий, преобразуем левую
часть (47):
MM{X
ν
|F
0
}χ{A} = MM{X
ν
χ{A}|F
0
} = MX
ν
χ{A}.
Тем самым доказательство теоремы свелось к доказательству того, что
MX
ν
χ{A} = MX
0
χ{A} при любом A ∈ F
0
. (48)
Лемма 9.3. Если (X
n
, F
n
) — мартингал, A ∈ F
0
и ν — момент остановки
относительно {F
n
}, для которого выполнено (45), то при любом n ≥ 0
MX
0
χ{A} = MX
min{n,ν}
χ{A} = (49)
= MX
ν
χ{A ∩ {ν ≤ n}} + MX
n
χ{A ∩ {ν > n}}.
Доказательство. Первое равенство в лемме 9.3 является непосредственным
следствием леммы 9.2, согласно которой (X
min{n,ν}
, F
n
) — мартингал: действительно,
так как A ∈ F
0
, то
MX
min{n,ν}
χ{A} = MM{X
min{n,ν}
χ{A}|F
0
} =
= Mχ{A}M{X
min{n,ν}
|F
0
} = Mχ{A}X
0
.
Второе равенство соответствует определению MX
min{n,ν}
χ{A}.
Заметим теперь, что левая часть (49) не зависит от n и что второе слагаемое в
правой части (49) по условию (45) стремится к 0 по некоторой подпоследовательности
60
