Зубков А.М. Конспект лекций по теории случайных процессов
Подождите немного. Документ загружается.


Доказательство. Допустим противное: lim
n→∞
X
n
с положительной вероятностью
не существует, т.е.
P{ξ
∗
= lim inf
n→∞
X
n
< lim sup
n→∞
X
n
= ξ
∗
} > 0. (50)
Пусть Q — множество всех рациональных чисел. Так как
{ξ
∗
< ξ
∗
} =
[
a,b∈Q: a<b
{ω: ξ
∗
< a < b < ξ
∗
},
то
0 < P{ξ
∗
< ξ
∗
} ≤
X
a,b∈Q: a<b
P{ξ
∗
< a < b < ξ
∗
}.
Так как множество Q
2
счетно, то существуют такие a, b ∈ Q, что
p = P{ξ
∗
= lim inf
n→∞
X
n
< a < b lim sup
n→∞
X
n
= ξ
∗
} > 0. (51)
Пусть β
∗
(a, b) = sup
n
β
n
(a, b); тогда β
n
(a, b) ↑ β
∗
(a, b) при n ↑ ∞. Если выполняется
(51), то P{β
n
(a, b) > k} → p, n → ∞ при любом k < ∞; поэтому P{β
∗
(a, b) = ∞} > 0
и Mβ
∗
(a, b) = ∞. Но согласно неравенству Дуба
Mβ
n
(a, b) ≤
M(X
n
− a)
+
b − a
≤
M(X
n
)
+
+ |a|
b − a
,
т. е.
Mβ
∗
(a, b) = lim
n→∞
Mβ
n
(a, b) ≤
1
b − a
sup
n
MX
+
n
+ |a| < ∞,
так как MX
+
n
≤ M|X
n
|. Полученное противоречие показывает, что предположение
(50) было неверно, значит, с вероятностью 1 существует lim
n→∞
X
n
= X, и по
лемме Фату M|X| ≤ sup M|X
n
| < ∞ (как интеграл от предела последовательности
неотрицательных функций). Теорема доказана.
Следствие 9. 1. Если X
n
≤ 0 — субмартингал, то
P{∃ lim
n→∞
X
n
< ∞} = 1.
Для доказательства достаточно заметить, что в этом случае M|X
n
| монотонно
убывает и, следовательно, ограничен сверху M|X
0
|.
Следствие 9.2. Если {X
n
, F
n
} — неотрицательный мартингал, то
P{∃ lim
n→∞
X
n
< ∞} = 1.
Действительно, в этом случае M|X
n
| = sup
n
MX
n
= MX
1
< ∞.
Следствие 9.3 (Теорема Колмогорова о сходимости рядов). Пусть случайные
величины ξ
1
, ξ
2
, . . . независимы,
Mξ
k
= 0, Dξ
k
= σ
2
k
,
∞
X
k=1
σ
k
< σ
2
< ∞.
71

Тогда существует такая случайная величина S, что S
n
= ξ
1
+ . . . + ξ
n
→ S почти
наверное.
Доказательство. Последовательность {S
n
} — мартингал. Так как согласно
неравенству Иенсена MX
2
≥ (M|X|)
2
, то
M|S
n
| ≤ (MS
2
n
)
1/2
≤
Ã
n
X
k=1
σ
2
k
!
1/2
≤ σ < ∞,
т. е. условия теоремы о сходимости субмартингалов выполнены.
Теорема 9.6. Пусть µ(t) — ветвящийся процесс Гальтона–Ватсона с
производящей функцией числа потомков одной частицы f (s) 6= s. Случайный
процесс X(t) = µ(t)/A
t
при t → ∞ с вероятностью 1 сходится к случайной величине
X, MX < ∞. Характеристическая функция ψ(u) = Me
iuX
случайной величины X
удовлетворяет уравнению
ψ(Au) = f(ψ(u)).
Доказательство. Первое утверждение получается непосредственным применением
следствия 2 из теоремы о сходимости полумартингалов, так как X(t) —
неотрицательный мартингал.
Для доказательства второго утверждения заметим, что
ψ
t+1
(u)
def
= Me
iuX(t+1)
= M exp
n
iu
µ(t+1)
A
t+1
o
=
ϕ
¡
t + 1, exp
©
iu/A
t+1
ª¢
= f
¡
ϕ
¡
t, exp
©
iu/A
t+1
ª¢¢
= (52)
== f
³
M exp
n
iu
µ(t)
A
t+1
o´
= f
¡
Me
iuX(t)/A
¢
= f(ψ
t
(u/A)).
По доказанному X(t) → X при t → ∞, следовательно, ψ
t
(u) → ψ(u) при всех
действительных u. Переходя к пределу по t в обеих частях (52), получаем: ψ(u) =
f(ψ(u/A)), что лишь заменой переменных отличается от утверждения теоремы.
Утверждение теоремы 9.6 верно при любых значениях A, но оно не всегда
содержательно. Например, мы уже знаем, что при A 6 1 ветвящийся процесс
вырождается с вероятностью 1. Так что хотя при A < 1 величина 1/A
t
→ ∞,
предельная случайная величина X равна 0 с вероятностью 1 (вырождена), и ее
характеристическая функция ψ(u) ≡ 1 удовлетворяет уравнению, указанному в
условии, но это уравнение тривиально. То же самое относится и к критическим
процессам. При A > 1 ветвящийся процесс с положительной вероятностью
не вырождается, но предельная случайная величина X имеет невырожденное
распределение только при дополнительном условии Mγ ln(γ + 1) < ∞.
10. Процесс броуновского движения
Определение. Процессом броуновского движения (или стандартным
винеровским процессом) w
t
, t ∈ [0, ∞) называется случайный процесс,
конечномерные распределения которого обладают следующими свойствами:
а) P{w(0) = 0} = 1,
72

б) для любых 0 = t
0
< t
1
< . . . < t
n
случайные величины w(t
1
) − w(t
0
), w(t
2
) −
w(t
1
), . . . , w(t
n
) − w(t
n−1
) независимы,
в) w(t) − w(s) при 0 ≤ s ≤ t имеет нормальное распределение с математическим
ожиданием 0 и дисперсией t − s.
Условие согласованности конечномерных распределений стандартного
винеровского процесса (как процесса с независимыми приращениями) легко
проверяется: если t
1
< t
2
< . . . < t
n
, то из свойств б), в) следует, что если случайные
величины ∆
2
, . . . , ∆
n
независимы и ∆
k
имеет такое же нормальное распределение
N(0, t
k
− t
k−1
), как w(t
k
) − w(t
k−1
) при всех k = 2, . . . , n, то сумма
∆
2
+ . . . + ∆
n
имеет нормальное распределение с математическим ожиданием 0 и дисперсией [t
2
−
t
1
] + [t
3
−t
2
] + . . . + [t
n
−t
n−1
] = t
n
−t
1
, т.е. такое же распределение, как w(t
n
) −w(t
1
).
В случае произвольного винеровского процесса параметры нормального
распределения w(t) − w(s) могут более сложным образом зависеть от t, s и от w(s).
Одной из интерпретаций винеровского процесса является модель движения
маленькой частицы, взвешенной в жидкости и совершающей хаотическое движение
в результате столкновений с молекулами жидкости. Впервые такое явление отметил
в своей статье голландец ван Ливенхок в XVII веке, наблюдавший под микроскопом
частицы пыльцы в водном растворе, а английский ботаник Броун в 1828 г. подробно
описал свойства этого движения. Движение мелких частиц наблюдали и многие
другие, но Броун был первым, кто осознал, что наблюдаемое хаотическое движение —
это не просто досадная помеха, мешающая разглядывать мелкие частицы вещества,
а проявление закона природы. В 1900 г. французский математик Башелье в своей
диссертации предложил то, что теперь называют винеровским процессом, в качестве
математической модели процесса изменения цен на акции, но его работа осталась
почти незамеченной. Затем модели хаотического движения использовали в своих
работах по статистической физике Эйнштейн (1905), Ланжевен (1909), Орнштейн и
Уленбек (1930). Математически строгую теорию броуновского движения построил
в 1923 г. Винер, который описал соответствующее распределение на множестве
непрерывных функций, однако значение его работы было понято только после
создания аксиоматической теории вероятностей А.Н.Колмогоровым в 1931 г.
Лемма 10.1. Совместное распределение значений процесса броуновского
движения w(t
1
), . . . , w(t
n
) при любых 0 = t
0
< t
1
< . . . < t
n
, n = 1, 2, . . .,
является многомерным нормальным распределением с нулевым вектором средних
и ковариационной матрицей Σ = kmin{t
i
, t
j
}k
n
i,j=1
.
Доказательство. Приращения процесса броуновского движения на интервалах
(0, t
1
) = (t
0
, t
1
), . . . , (t
n−1
, t
n
) независимы и имеют нормальные распределения с
параметрами (0, t
j
− t
j−1
), j = 1, . . . , n. Поэтому вектор приращений (w(t
1
) −
w(t
0
), w(t
2
)−w(t
1
), . . . , w(t
n
)−w(t
n−1
)) имеет многомерное нормальное распределение
с независимыми компонентами и плотностью
p
∆
t
1
,...,t
n
(y
1
, . . . , y
n
) =
n
Y
j=1
1
p
2π(t
j
− t
j−1
)
exp
½
−
y
2
j
2(t
j
− t
j−1
)
¾
.
73

Переход от вектора приращений
(y
1
, y
2
, . . . , y
n
) = (w(t
1
) − w(t
0
), w(t
2
) − w(t
1
), . . . , w(t
n
) − w(t
n−1
))
к вектору (w(t
1
), w(t
2
), . . . , w(t
n
)) значений процесса соответствует линейному
преобразованию
(y
1
, y
2
, . . . , y
n
) → (y
1
, y
1
+ y
2
, y
1
+ y
3
, . . . , y
1
+ y
2
+ . . . + y
n
) = (y
1
, y
2
, . . . , y
n
)A
с матрицей
A =
°
°
°
°
°
°
°
°
°
°
1 1 1 . . . 1 1
0 1 1 . . . 1 1
0 0 1 . . . 1 1
. . . . . . . .
0 0 0 . . . 0 1
°
°
°
°
°
°
°
°
°
°
.
Линейное отображение переводит многомерное нормальное распределение
в многомерное нормальное распределение; при этом вектор математических
ожиданий умножается на матрицу отображения, а матрица ковариаций умножается
слева и справа на матрицу преобразования и на транспонированную матрицу.
В нашем случае как исходное, так и преобразованное распределения имеют
нулевое математическое ожидание, а матрицу ковариаций проще вычислить
непосредственно.
По определению Dw(t
j
) = t
j
, а при s < t ввиду независимости приращений
процесса на непересекающихся интервалах
cov(w(s), w(t)) = cov(w(s) − w(0), (w(s) − w(0)) + (w(t) − w(s))) =
= cov(w(s), w(s)) = Dw(s) = s.
Таким образом,
Σ =
°
°
°
°
°
°
°
°
°
°
t
1
t
1
t
1
. . . t
1
t
1
t
1
t
2
t
2
. . . t
2
t
2
t
1
t
2
t
3
. . . t
3
t
3
. . . . . . . .
t
1
t
2
t
3
. . . t
n−1
t
n
°
°
°
°
°
°
°
°
°
°
= kmin{t
i
, t
j
}k
n
i,j=1
.
Тем самым лемма доказана.
Вычислим плотность совместного распределения значений
(w(t
1
), w(t
2
), . . . , w(t
n
)). Если ξ = (ξ
1
, . . . , ξ
n
) — случайный вектор с плотностью
распределения p(x) и отображение H = (H
1
, . . . , H
n
) : R
n
→ R
n
однозначно
обратимо, то случайный вектор ζ = H(ξ) имеет плотность q(x) =
p(H
−1
(x))
J
H
(H
−1
(x))
, где
J
H
(x) =
¯
¯
¯
det
°
°
°
∂H
i
(x)
∂x
j
°
°
°
¯
¯
¯
— якобиан отображения H в точке x.
Якобиан линейного отображения с матрицей A тождественно равен 1, поэтому
плотность p
t
1
,...,t
n
(x
1
, . . . , x
n
) распределения вектора (w(t
1
), w(t
2
), . . . , w(t
n
)) в точке
x = (x
1
, . . . , x
n
) равна плотности распределения вектора (w(t
1
) − w(t
0
), w(t
2
) −
74
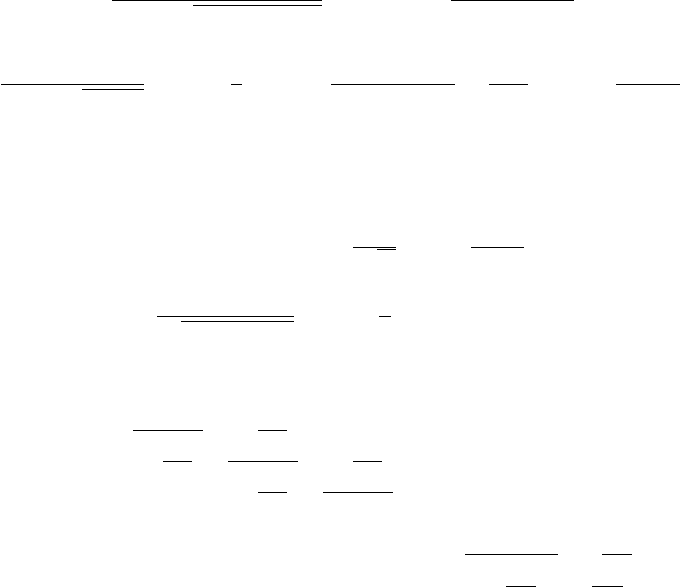
w(t
1
), . . . , w(t
n
) − w(t
n−1
)) в точке (x
1
, x
2
− x
1
, . . . , x
n
− x
n−1
), т.е.
p
t
1
,...,t
n
(x
1
, . . . , x
n
) = p
∆
t
1
,...,t
n
(x
1
, x
2
− x
1
, . . . , x
n
− x
n−1
) =
=
1
Q
n
j=1
p
2π(t
j
− t
j−1
)
exp
(
−
n
X
j=1
(x
j
− x
j−1
)
2
2(t
j
− t
j−1
)
)
=
=
1
Q
n
j=1
p
2π∆t
j
exp
(
−
1
2
Ã
n−1
X
j=1
x
2
j
∆t
j+1
+ ∆t
j
∆t
j
∆t
j+1
+
x
2
n
∆t
n
− 2
n−1
X
j=1
x
i
x
j+1
∆t
j+1
!)
,
где ∆t
j
= t
j
− t
j−1
, j = 1, ..., n, t
0
= 0.
Плотность невырожденного n-мерного нормального распределения с вектором
математических ожиданий a и матрицей ковариаций Σ (по аналогии с плотностью
одномерного нормального распределения
1
σ
√
2π
exp{−
(x−a)
2
2σ
2
}) имеет вид
p(x) =
1
p
(2π)
n
det Σ
exp
½
−
1
2
(x − a)Σ
−1
(x − a)
T
¾
,
где T — символ транспонирования. Таким образом, в нашем случае
Σ
−1
=
°
°
°
°
°
°
°
°
°
°
°
°
°
∆t
1
+∆t
2
∆t
1
∆t
2
−
1
∆t
2
0 . . . 0 0
−
1
∆t
2
∆t
3
+∆t
2
∆t
2
∆t
3
−
1
∆t
3
. . . 0 0
0 −
1
∆t
3
∆t
4
+∆t
3
∆t
3
∆t
4
. . . 0 0
. . . . . . . .
0 0 0 . . .
∆t
n
+∆t
n−1
∆t
n−1
∆t
n
−
1
∆t
n
0 0 0 . . . −
1
∆t
n
1
∆t
n
°
°
°
°
°
°
°
°
°
°
°
°
°
.
Определение. Случайные процессы ξ(t) и η(t), t ∈ T , называются стохастически
эквивалентными (или просто эквивалентными), если P{ξ(t) = η(t)} = 1 при всех
t ∈ T . Случайный процесс η(t), стохастически эквивалентный случайному процессу
ξ(t), называют модификацией процесса ξ(t).
У эквивалентных случайных процессов ξ(t) и η(t) любые конечномерные
распределения совпадают, так как
P{ξ(t
i
) = η(t
i
), i = 1, . . . , n} = 1 при любых t
1
< t
2
< . . . < t
n
.
Пример 10.1. Пусть ξ(t) ≡ 0, t ∈ [0, 1], — случайный процесс, траектории которого
тождественно равны 0. Введем функцию r(t), которая равна 1, если t принадлежит
множеству Q рациональных чисел, и равна 0 в остальных случаях. Пусть γ —
случайная величина, равномерно распределенная на [0, 1]. Рассмотрим случайный
процесс η(t) = r(t + γ). Тогда при любом t ∈ [0, 1]
P{ξ(t) 6= η(t)} = P{r(t + γ) = 1} = P {γ + t ∈ Q} = 0,
т.е. ξ(t) и η(t) эквивалентны и все их конечномерные распределения совпадают.
Однако легко указать свойство, различающее эти процессы с вероятностью 1:
P{ sup
t∈[0,1]
ξ(t) = 0} = 1, P{ sup
t∈[0,1]
η(t) = 1} = 1.
75

Этот пример показывает, что для любого процесса имеется бесконечное
множество эквивалентных ему процессов, обладающих отличными от него
вероятностными свойствами. Однако в более узких классах случайных процессов
(например, в классе процессов с непрерывными траекториями) такие примеры
построить нельзя.
Утверждение 10.1. Пусть ξ(t) и η(t), t ∈ [0, 1], — два случайных процесса,
определенных на одном и том же вероятностном пространстве. Если существуют
такое счетное детерминированное множество A ⊂ [0, 1] и такой функционал F:
R
A
→ R
[0,1]
, что P{ξ(x) = η(x)} = 1 для любого x ∈ A и
P{ξ(t) = F ({ξ(x)}
x∈A
)(t) ∀t ∈ [0, 1]} =
= P{η(t) = F ({η(x)}
x∈A
)(t) ∀t ∈ [0, 1]} = 1,
то
P{ξ(t) = η(t) ∀t ∈ [0, 1]} = 1.
Действительно, при этих условиях
{ξ(t) = η(t) ∀t ∈ [0, 1]} = {ξ(x) = η(x) ∀x ∈ A},
а P{ξ(x) = η(x) ∀x ∈ A} = 1 как вероятность пересечения счетного множества
событий, имеющих единичные вероятности.
Условиям утверждения 10.1 удовлетворяют случайные процессы, траектории
которых с вероятностью 1 непрерывны (тогда в качестве A можно взять
множество рациональных чисел) или имеют только изолированные точки разрыва.
Значит, вероятностные свойства случайных процессов с непрерывными (или
имеющими только изолированные разрывы) траекториями однозначно определяются
свойствами их конечномерных распределений. Следующая теорема указывает
условия существования непрерывной модификации случайного процесса в терминах
конечномерных распределений.
Теорема 10.1 (Колмогоров). Пусть ξ(t) — случайный процесс на [0, 1]. Если
существуют такие b > a > 0, c < ∞, что при любых t, t + h ∈ [0, 1]
M|ξ(t + h) − ξ(t)|
a
≤
c|h|
|log |h||
1+b
(53)
то ξ(t) имеет непрерывную модификацию.
Доказательство. Пусть выполнено условие (1). Будем использовать обозначение
∆
h
ξ(t) = ξ(t + h) − ξ(t). Тогда по неравенству Чебышева при ε(h) = |log |h||
−β
, 1 <
β < b/a ,
P{|∆
h
ξ(t)| > ε(h)} 6
M|∆
h
ξ(t)|
a
ε
a
(h)
6
c|h|
|log |h||
1+b−aβ
=
c|h|
|log |h||
1+δ
def
= q(h), (54)
где δ = b − aβ > 0. Заметим, что ε(h) ↓ 0 и q(h) ↓ 0 при |h| ↓ 0. Кроме того, из
определений функций ε(h) и q(h)следует, что
∞
X
n=1
ε
¡
1
2
n
¢
=
∞
X
n=1
c
∗
n
β
< ∞,
∞
X
n=1
2
n
q
¡
1
2
n
¢
=
∞
X
n=1
c
∗∗
n
1+δ
< ∞.
76
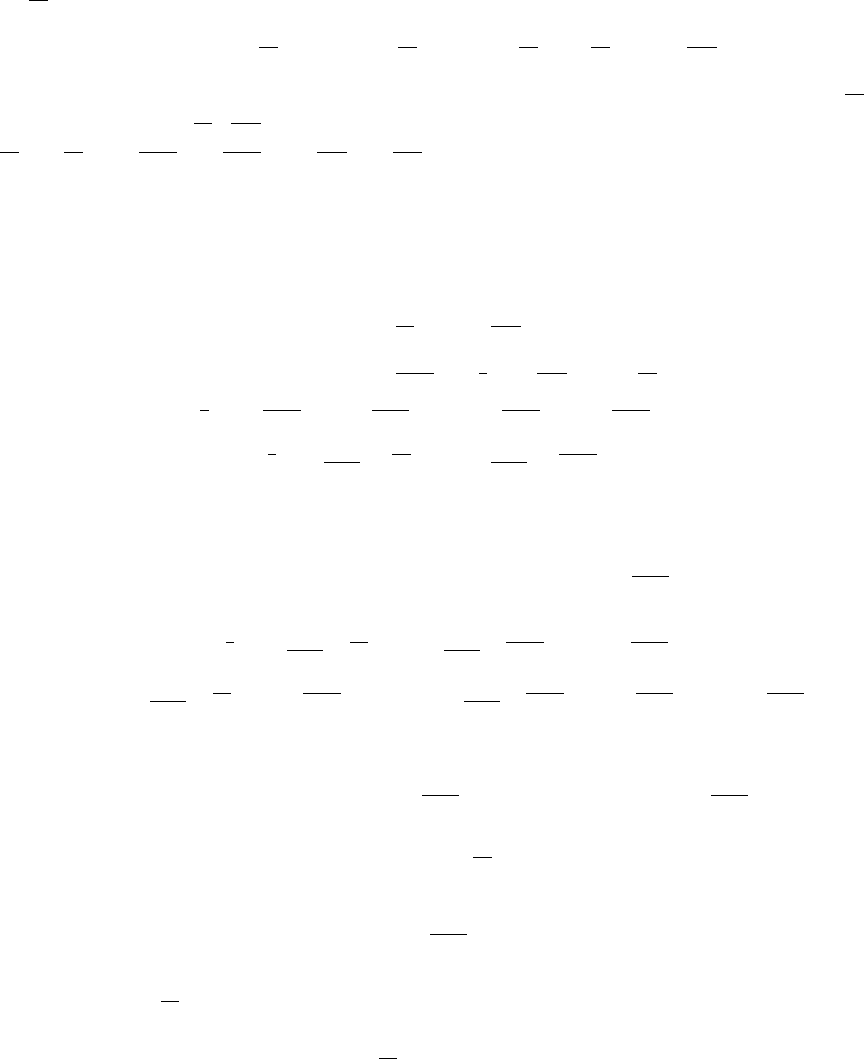
Построим последовательность непрерывных случайных процессов ξ
n
(t), которая
при n → ∞ будет равномерно по t ∈ [0, 1] сходиться к предельному случайному
процессу η(t). Определим ξ
n
(t) как непрерывную функцию, совпадающую с ξ(t) при
t =
r
2
n
, r = 0, 1, . . . , 2
n
, и линейную между этими точками:
ξ
n
(t) = ξ
¡
r
2
n
¢
+ 2
n
¡
t −
r
2
n
¢
∆
1/2
n
ξ
¡
r
2
n
¢
,
r
2
n
6 t 6
r+1
2
n
.
Таким образом, траектории процессов ξ
n
(t) и ξ
n+1
(t) совпадают в точках вида
r
2
n
, и
на любом отрезке
£
r
2
n
,
r+1
2
n
¤
их графики образуют треугольник с вершинами в точках
¡
r
2
n
, ξ
¡
r
2
n
¢¢
,
¡
2r+1
2
n+1
, ξ
¡
2r+1
2
n+1
¢¢
,
¡
r+1
2
n
, ξ
¡
r+1
2
n
¢¢
.
Дальнейшее доказательство разобьем на две леммы.
Лемма 10.2. Последовательность ξ
n
(t) при n → ∞ с вероятностью 1
сходится равномерно по t ∈ [0, 1] к предельному случайному процессу η(t), который
непрерывен с вероятностью 1.
Лемма 10.3. Случайные процессы ξ(t) и η(t) эквивалентны.
Доказательство леммы 10.2. Если
r
2
n
6 t 6
r+1
2
n
, то
|ξ
n+1
(t) − ξ
n
(t)| 6
¯
¯
ξ
¡
2r+1
2
n+1
¢
−
1
2
¡
ξ
¡
r+1
2
n
¢
+ ξ
¡
r
2
n
¢¢
¯
¯
=
=
1
2
¯
¯
¡
ξ
¡
2r+1
2
n+1
¢
− ξ
¡
2r
2
n+1
¢¢
+
¡
ξ
¡
2r+1
2
n+1
¢
− ξ
¡
2r+2
2
n+1
¢¢
¯
¯
6
6
1
2
h
¯
¯
¯
∆
1
2
n+1
ξ
¡
r
2
n
¢
¯
¯
¯
+
¯
¯
¯
∆
1
2
n+1
ξ
¡
2r+1
2
n
¢
¯
¯
¯
i
.
Значит, в силу (54)
P
n,r
def
= P
(
sup
r/2
n
6t6(r+1)/2
n
|ξ
n+1
(t) − ξ
n
(t)| > ε
¡
1
2
n+1
¢
)
6
6 P
n
1
2
³
|∆
1
2
n+1
ξ(
r
2
n
)| + |∆
1
2
n+1
ξ(
2r+1
2
n+1
)|
´
> ε(
1
2
n+1
)
o
6
6 P
n
|∆
1
2
n+1
ξ(
r
2
n
)| > ε(
1
2
n+1
)
o
+ P
n
|∆
1
2
n+1
ξ(
2r+1
2
n+1
)| > ε(
1
2
n+1
)
o
6 2q(
1
2
n+1
).
Далее,
P
½
sup
06t61
|ξ
n+1
(t) − ξ
n
(t)| > ε
¡
1
2
n+1
¢
¾
6
2
n
−1
X
r=0
P
n,r
6 2
n+1
q
¡
1
2
n+1
¢
.
По определению функции q ряд
P
∞
n=1
2
n
q(
1
2
n
) сходится; следовательно, согласно
лемме Бореля–Кантелли для почти всех ω ∈ Ω существует такое n(ω) < ∞, что
sup
t∈[0,1]
|ξ
n+1
(t) − ξ
n
(t)| < ε
¡
1
2
n+1
¢
при всех n > n(ω).
Но ряд
P
n≥1
ε
¡
1
2
n
¢
тоже сходится, поэтому с вероятностью 1
sup
t∈[0,1]
|ξ
n
(t) − ξ
m
(t)| 6
X
k>n
ε
¡
1
2
k
¢
def
= ε
n
→ 0 при m, n → ∞, m > n.
Значит, последовательность {ξ
n
(t)} почти наверное фундаментальна и для почти
всех ω существует lim
n→∞
ξ
n
(t) = η(t), более того,
sup
t∈[0,1]
|ξ
n
(t) − η(t)| 6 ε
n
при всех n > n(ω),
77
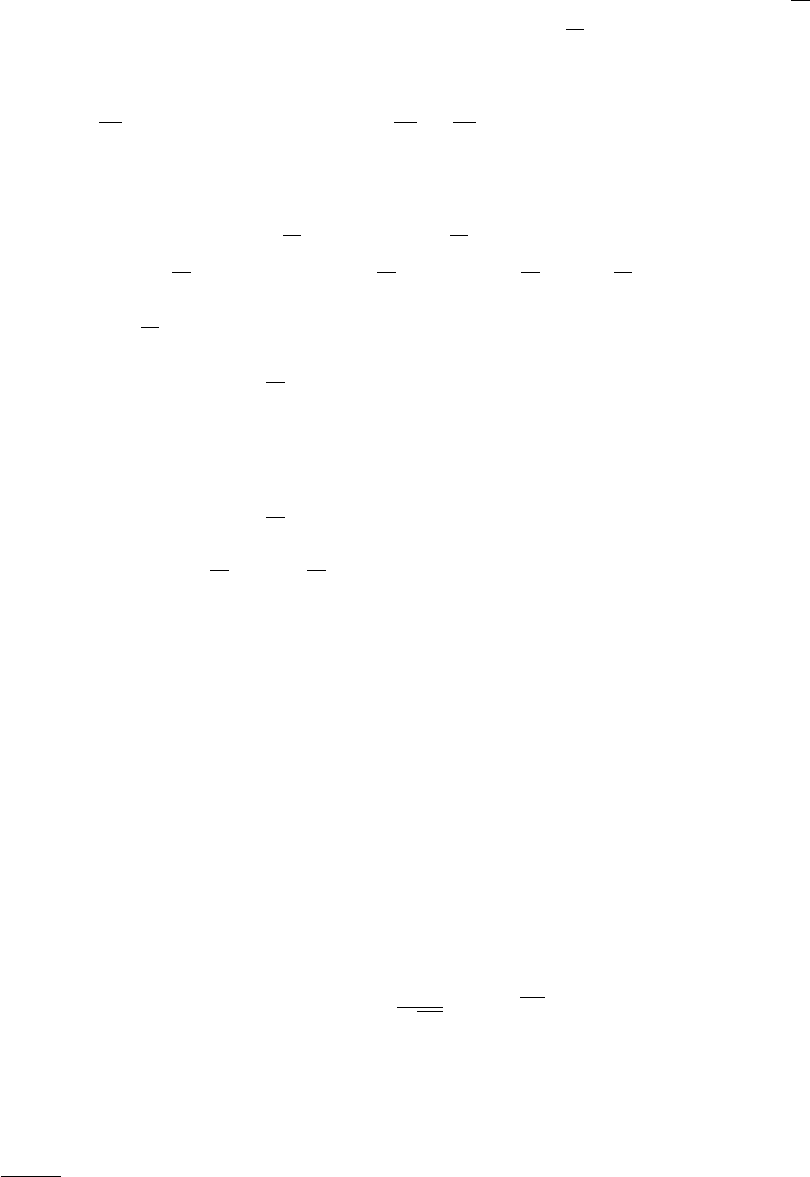
т.е. для почти всех ω ∈ Ω сходимость ξ
n
(t) → η(t) (n → ∞) равномерна на [0, 1]. Так
как траектории ξ
n
(t) непрерывны, то и их равномерные пределы непрерывны, т.е.
случайный процесс η(t) непрерывен почти наверное. Лемма 10.2 доказана.
Доказательство леммы 10.3. Покажем, что ξ(t) и η(t) эквивалентны, т. е. что
P{ξ(t) = η(t)} для любого t ∈ [0, 1]. Для этого заметим сначала, что если t =
r
2
n
,
то ξ
n+k
(t) = ξ(t) = η(t) для каждого k > 0. Если же t /∈ {
r
2
n
, r, n ∈ {0, 1, . . .}}, то
числа r
n
= [t2
n
] удовлетворяют условиям
r
n
2
n
→ t (n → ∞), 0 < t −
r
n
2
n
<
1
2
n
(n = 1, 2, . . .).
Тогда согласно (54)
P
©
¯
¯
ξ
¡
r
n
2
n
¢
− ξ(t)
¯
¯
> ε
¡
1
2
n
¢ª
6
6 P
©
¯
¯
ξ
¡
r
n
2
n
¢
− ξ(t)
¯
¯
> ε
¡
t −
r
n
2
n
¢ª
6 q
¡
t −
r
n
2
n
¢
6 q
¡
1
2
n
¢
.
Так как ряд
P
n>1
q
¡
1
2
n
¢
сходится, то по лемме Бореля–Кантелли для каждого t
P
©
ξ
¡
r
n
2
n
¢
→ ξ(t), n → ∞
ª
= 1. (55)
С другой стороны, согласно лемме 1 траектории случайного процесса η(t) с
вероятностью 1 непрерывны, т.е. для каждого t
P
©
η
¡
r
n
2
n
¢
→ η(t), n → ∞
ª
= 1. (56)
Из равенств (55), (56) и ξ
¡
r
n
2
n
¢
= η
¡
r
n
2
n
¢
следует теперь, что P{ξ(t) = η(t)} = 1 при
любом t. Тем самым лемма 3 и теорема доказаны.
Пример 10.2: пуассоновский процесс. Если ξ(t) — пуассоновский процесс с
интенсивностью λ, то его траектории разрывны; для такого процесса при любом
a > 0
M|ξ(t + h) − ξ(t)|
a
> P{ξ(t + h) > ξ(t)} = λh + o(h), h ↓ 0,
т. е. условия теоремы Колмогорова не выполняются, однако отличие состоит только в
отсутствии медленно убывающего при h → 0 множителя |ln |h||
−1−b
. Это показывает,
что условия теоремы близки к необходимым.
Следствие. Винеровский процесс имеет модификацию, траектории которой с
вероятностью 1 непрерывны.
Доказательство. Воспользуемся теоремой Колмогорова об условиях
существования непрерывной модификации случайного процесса с a = 4:
M(w(t + h) − w(t))
4
=
1
√
2π
∞
Z
−∞
u
4
e
u
2
2|h|
du.
Четвертый момент (эксцесс) стандартного нормального распределения N(0, 1) с
нулевым средним и единичной дисперсией равен 3; в нашем случае w(t + h) − w(t)
имеет нормальное распределение N(0, |h|) c дисперсией |h|, значит, его эксцесс равен
3h
2
= o(
h
(klnh|)
6
, h ↓ 0.
78
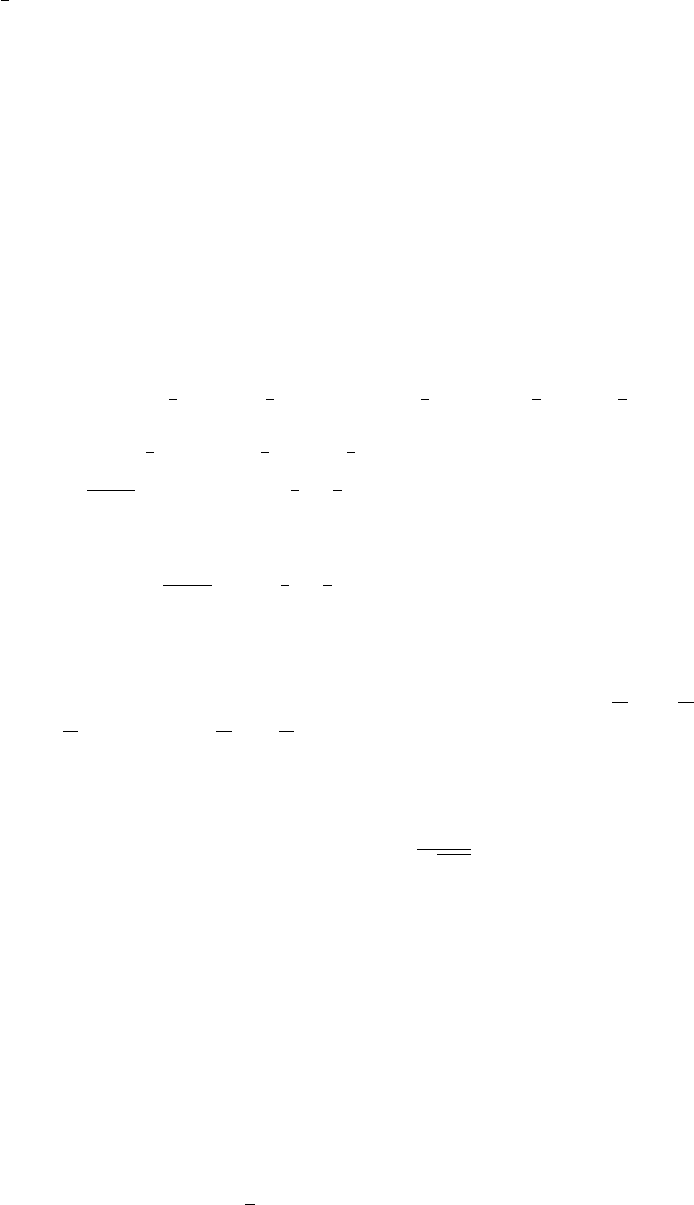
Лемма 10.4. Винеровский процесс w(t), t ≥ 0, имеет такие же конечномерные
распределения, как случайные процессы w
a
(t) = a
−1/2
w(at), t ≥ 0, где a > 0 — любое,
и w
∗
(t) = tw
¡
1
t
¢
, t ≥ 0.
Доказательство. Проверим для каждого из процессов w
a
(t) и w
∗
(t) выполнение
условий а)–в) из определения стандартного винеровского процесса. Для процесса w
a
условие а), т.е. P {w
a
(t) = 0} = 1, очевидно, выполняется; для процесса w
∗
(t) это
условие проверим позже.
Условие б) выполняется как для w
a
(t), так и для w
∗
(t), поскольку используемые
при переходе от w(t) к этим процессам преобразования оси времени монотонны,
значит, любые непересекающиеся интервалы они переводят в непересекающиеся
интервалы, и тогда независимые приращения процессов на интервалах-прообразах
переходят в независимые приращения на образах.
Проверка условия в) сводится к простым вычислениям: если 0 < s < t, то w
a
(t) −
w
a
(s) = a
−1/2
(w(at) − w(as)) имеет нормальное распределение N(0, t − s), так как
w(at) − w(as) имеет распределение N(0, a(t − s)); с другой стороны,
w
∗
(t) − w
∗
(s) = tw
¡
1
t
¢
− sw
¡
1
s
¢
= (t − s)w
¡
1
t
¢
− s
¡
w
¡
1
s
¢
− w
¡
1
t
¢¢
и по свойству б) (t − s)w
¡
1
t
¢
и s
¡
w
¡
1
s
¢
− w
¡
1
t
¢¢
независимы и имеют нормальные
распределения N
³
0,
(t−s)
2
t
´
и N
¡
0, s
2
¡
1
s
−
1
t
¢¢
соответственно, значит, их сумма
w
∗
(t) − w
∗
(s) имеет нормальное распределение
N
³
0,
(t−s)
2
t
+ s
2
¡
1
s
−
1
t
¢
´
= N(0, t − s).
Непрерывность траекторий w
∗
(t) следует из теоремы Колмогорова (так как
двумерные распределения, определяющие распределения приращений w
∗
(t) и w(t),
совпадают). Следовательно, w
∗
(0) = 0 как предельная точка для w
∗
¡
1
N
¢
=
1
N
w(N)
при N → ∞: Mw
∗
¡
1
N
¢
= 0, Dw
∗
¡
1
N
¢
=
1
N
. Лемма доказана.
Лемма 10.5. Справедливо соотношение
P
½
sup
0≤u≤t
w(u) ≥ x
¾
= 2P{w(t) ≥ x} =
2
√
2πt
∞
Z
x
e
−v
2
/2t
dv.
Доказательство. Аналогично доказательствам неравенств для функции
распределения максимумов случайных блужданий и мартингалов введем случайную
величину τ
x
= inf{u : w(u) > x}. Она определена, так как траектории w(t) с
вероятностью 1 непрерывны. Так же, как и для последовательностей, τ
x
есть момент
остановки:
{τ
x
> v} =
½
sup
06u6v
w(u) < x
¾
∈ F
v
def
= σ{w (u), u 6 v},
{τ
x
= v} =
∞
\
n=1
(
sup
06u6v−
1
n
w(u) < x, sup
06u6v
w(u) = x
)
∈ F
v
.
79

Значит, при τ
x
= v, v 6 t, величина w(t)−w(v) = w(t)−w(τ
x
) не зависит от поведения
процесса w(u) на [0, v] и имеет распределение N(0, t −v), т. е. для каждых v ∈ [0, t] и
x > 0
P{w(t) > x|τ
x
= v} =
1
2
, или P{w(t) > x|τ
x
} =
1
2
.
Вычисляя математическое ожидание по τ
x
, завершаем доказательство:
P{w(t) > x} = MP{w(t) > x|τ
x
}χ{τ
x
6 t} =
=
1
2
P{τ
x
6 t} =
1
2
P
½
sup
06u6v
w(u) > x
¾
.
Теорема 10.2 (Закон повторного логарифма). Для процесса броуновского
движения справедливы соотношения
P
½
lim sup
t→∞
w(t)
√
2t ln ln t
= 1
¾
= P
½
lim inf
t→∞
w(t)
√
2t ln ln t
= −1
¾
= 1,
P
lim sup
t↓0
w(t)
q
2t ln ln
1
t
= 1
= P
lim inf
t↓0
w(t)
q
2t ln ln
1
t
= −1
= 1.
Доказательство. Заметим прежде всего, что в силу леммы 2 распределения
случайных процессов
w(t)
√
2t ln ln t
и
tw(
1
t
)
√
2t ln ln t
=
w(u)
q
2u ln ln
1
u
, u =
1
t
,
совпадают, и так как u =
1
t
→ ∞, когда t → 0, то второе утверждение теоремы
следует из первого.
В начале этого курса был доказан закон повторного логарифма для случайного
блуждания {S
n
}, построенного по последовательности независимых случайных
величин, имеющих стандартные нормальные распределения. Последовательность
значений w(n) образует именно такое случайное блуждание: приращения w(n) −
w(n − 1) независимы и имеют стандартные нормальные распределения, так что
последовательность {w(n), n > 0} имеет такое же распределение, как {S
n
}. Поэтому
закон повторного логарифма для стандартного винеровского процесса вытекает из
закона повторного логарифма для случайного блуждания {S
n
} и из следующего
утверждения.
Лемма 10.4. Справедливо соотношение
P
½
lim sup
t→∞
¯
¯
¯
¯
w(t)
√
2t ln ln t
−
w([t])
√
2t ln ln t
¯
¯
¯
¯
= 0
¾
= 1.
Доказательство леммы 10.4. Из определения винеровского процесса и из леммы
10.3 следует, что при любом n = 0, 1, . . .
P
½
sup
n6t6n+1
|w(t) − w(n)| > x
¾
6 P
½
sup
06t61
w(t) > x
¾
+ P
½
inf
06t61
w(t) < −x
¾
=
= 2P
½
sup
06t61
w(t) > x
¾
=
4
√
2π
∞
Z
x
e
−v
2
/2
dv <
2
x
e
−x
2
/2
, x > 0.
80
