Зубков А.М. Конспект лекций по теории случайных процессов
Подождите немного. Документ загружается.


Обозначим через µ(t) число частиц в его t-м поколении. Как установлено в теореме
1, среднее число потомков одной частицы равно λMγ
n
. В этом ветвящемся процессе
µ(0) = 1 (период занятости начинается с одной заявки), а общее число частиц до его
вырождения равно
P
t>0
µ(t). По свойствам ветвящихся процессов
Mµ(t) = (M{µ(1)|µ(0) = 1})
t
= (λMγ
n
)
t
.
Поэтому
M
X
t>0
µ(t) =
X
t>0
Mµ(t) =
X
t>0
(λMγ
n
)
t
=
1
1 − λMγ
n
.
Теорема доказана.
Отметим, что при λMγ
n
→ 1 среднее число требований, обслуженных за период
занятости, стремится к ∞; это значит, что при повышении нагрузки прибору
приходится работать почти безостановочно, и в силу неравномерности поступления
требований средний размер очереди тоже будет расти.
Мы определяли пуассоновский поток как такую случайную совокупность точек на
прямой, что числа точек, попадающие в непересекающиеся интервалы, независимы
и имеют пуассоновские распределения с параметрами, пропорциональными мерам
этих интервалов. Это определение непосредственно обобщается на случайные
совокупности точек в любом измеримом пространстве: пуассоновским полем
интенсивности λ в пространстве R
d
называется такая случайная совокупность точек,
что для любого открытого множества A ∈ R
d
число точек, попадающих в A,
имеет распределение Пуассона с параметром λ mes(A). Наглядными примерами
пуассоновских полей являются пятна от капель начинающегося дождя на асфальте
и взвесь мелких частиц в сосуде с хорошо перемешанной водой.
Пример 6.4 (измерение малых концентраций микробов). При оценке уровня
биологической загрязненности воды нужно измерять чрезвычайно малые
концентрации λ микробов (скажем, десятки микробов на литр воды). Чтобы
построить статистические оценки таких концентраций, берут N проб по z
миллилитров воды, каждую пробу процеживают, осадки помещают в N капель
питательной среды и выжидают время, достаточное для того, чтобы микробы
размножились и образовали отчетливо различимые колонии. Эти колонии могут
возникнуть в тех и только тех каплях, в которые попал хотя бы один микроб.
Если считать, что распределение микробов в воде описывается пуассоновским
полем с параметром λ, то вероятность того, что в объеме z не будет ни одного
микроба, равна вероятности того, что случайная величина, имеющая распределение
Пуассона с параметром λz, принимает значение 0, т. е. равна p = e
−λz
. Допустим,
что из N пробирок в ν пробирках микробов не оказалось. Вероятность такого исхода
равна
C
N
νp
ν
(1 − p)
N−ν
= C
ν
N
e
−λzν
(1 − e
−λz
)
N−ν
. (26)
В качестве оценки максимального правдоподобия параметра λ выбирают то его
значение, при котором вероятность наблюденного исхода эксперимента максимальна.
В нашем случае для того, чтобы найти это значение, нужно продифференцировать
41

по λ вероятность (26), приравнять производную 0 и решить полученное уравнение:
d
dλ
e
−λzν
(1 − e
−λz
)
N−ν
=
= e
−λzν
(1 − e
−λz
)
N−ν−1
[−zν(1 − e
−λz
) + (N − ν)ze
−λz
] = 0,
т.е.
ν = Ne
−λz
, e
−λz
=
ν
N
, λ =
1
z
ln
N
ν
.
Заметим, что при ν = 0 (во всех пробах оказались микробы) оценка для λ
оказывается равной ∞, и это в каком-то смысле естественно, потому что такой исход
эксперимента возможен при любой достаточно большой концентрации.
Задача 6.4. Как построить доверительный интервал для неизвестной
концентрации микробов λ, имеющий заданную доверительную вероятность α?
7. Цепи Маркова с непрерывным временем
Определение. Счетной цепью Маркова с непрерывным временем называется
такой случайный процесс {ξ(t), t ≥ 0}, что значения ξ(t) принадлежат не более чем
счетному множеству S и для любых n ≥ 1, 0 ≤ t
0
< t
1
< . . . < t
n
и i
0
, . . . , i
n
∈ S
P{ξ(t
n
) = i
n
|ξ(t
0
) = i
0
, ξ(t
1
) = i
1
, . . . , ξ(t
n−1
) = i
n−1
} =
= P{ξ(t
n
) = i
n
|ξ(t
n−1
) = i
n−1
}. (27)
Если стоящие в правой части (27) переходные вероятности цепи Маркова P{ξ(t+s) =
j|ξ(t) = i} не зависят от t:
P{ξ(t + s) = j|ξ(t) = i} = p
ij
(s),
то цепь ξ(t) называется однородной по времени.
Простым примером счетной цепи Маркова с непрерывным временем является
однородный пуассоновский процесс ξ(t) с параметром λ. Цепями Маркова являются
также некоторые функции от ξ(t), в частности, η
λ
(t) = ξ(t) (mod 2) (траектории η
λ
(t)
представляют собой ступенчатые функции, принимающие только 2 значения: 0 и 1).
Любой процесс с независимыми приращениями и дискретным множеством состояний
тоже является цепью Маркова.
Определению (27) удовлетворяют случайные процессы с «патологическими»
свойствами, например несчетная совокупность независимых одинаково
распределенных случайных величин {ξ
p
(t)}
t>0
:
P{ξ
p
(t) = 0} = 1 − p, P{ξ
p
(t) = 0} = p для всех t ≥ 0.
При 0 < p < 1 траектории цепи ξ
p
(t) представляют собой всюду разрывные функции,
которые на любых сколь угодно малых интервалах принимают оба значения 0 и 1.
(Такая цепь является предельной для последовательности цепей η
λ
(t) = ξ(t)(mod 2)
при λ → ∞.) Мы будем рассматривать только цепи Маркова, траектории которых не
42
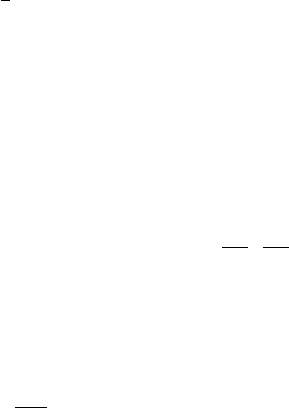
имеют точек разрыва второго рода (т.е. для любого t траектория цепи с вероятностью
1 имеет правый и левый пределы).
Определение. Цепь Маркова ξ(t) с непрерывным временем называется
стохастически непрерывной, если
P{ξ(t + s) = ξ(t)} → 1 при s ↓ 0.
В однородной по времени цепи Маркова ξ
t
с дискретным временем переходы
из состояния в состояние происходят только в целочисленные моменты времени, а
вероятности переходов определяются матрицей вероятностей переходов P = kp
ij
k.
Многие «естественные» цепи Маркова с непрерывным временем и не более чем
счетным множеством состояний S можно получить из цепей Маркова с дискретным
временем и тем же множеством состояний S, если заменить единичные времена
пребывания в состояниях независимыми случайными величинами, которые имеют
показательные распределения с параметрами, зависящими от состояния.
Проведем формальное построение однородной цепи Маркова с непрерывным
временем, множеством состояний S, матрицей вероятностей переходов в моменты
скачков P = kp
ij
k
i,j∈S
и множеством интенсивностей выходов Λ = {λ
i
, i ∈ S}. Мы
будем использовать следующие известные свойства показательного распределения:
1) если P{τ > x} = e
−x
, x > 0, то P
©
τ
λ
> x
ª
= e
−λx
, x > 0,
2) (отсутствие последействия) если P{τ > x} = e
−λx
, x > 0, то
P{τ > x + y |τ > x} = e
−λy
при любых x, y > 0.
Траекторию цепи Маркова с непрерывным временем можно построить по
траектории ξ
0
, ξ
1
, . . . цепи Маркова с дискретным временем и той же матрицей
переходных вероятностей P и по вспомогательной последовательности независимых
и не зависящих от ξ
0
, ξ
1
, . . . случайных величин τ
0
, τ
1
, . . . : P{τ
k
> u} = e
−u
, u > 0,
k = 0, 1, . . . При фиксированной траектории {ξ
n
} времена
τ
0
λ
ξ
0
,
τ
1
λ
ξ
1
, . . . пребываний
в состояниях независимы и имеют показательные распределения с параметрами
λ
ξ
0
, λ
ξ
1
, . . . соответственно. По {ξ
k
} и τ
k
построим возрастающую последовательность
случайных моментов времени (моментов переходов)
T
0
= 0, T
n
=
n−1
X
k=0
τ
k
λ
ξ
k
, n = 1, 2, . . . ,
и кусочно-постоянную функцию ξ(t):
ξ(t) = ξ
n
при T
n
6 t < T
n+1
. (28)
Таким образом, последовательность состояний, через которые проходит
траектория случайного процесса ξ(t), t ∈ [0, ∞), является цепью Маркова {ξ
n
} с
дискретным временем и матрицей переходных вероятностей P = kp
ij
k. Эта цепь
называется вложенной цепью Маркова для процесса ξ(t).
Утверждение 7.1. Если λ
∗
= sup
i∈S
λ
i
< ∞, то формула (28) определяет
случайный процесс ξ(t) на [0, ∞), который является цепью Маркова с непрерывным
временем.
43

Доказательство. Чтобы доказать, что формула (28) определяет процесс ξ(t) на
всей оси [0, ∞), достаточно показать, что T
n
→ ∞ при n → ∞ с вероятностью 1. Но
T
n
=
n−1
X
k=0
τ
k
λ
ξ
k
>
n−1
X
k=0
τ
k
λ
∗
=
1
λ
∗
n−1
X
k=0
τ
k
,
и по закону больших чисел P{
1
n
P
n−1
k=0
τ
k
→ Mτ
1
= 1, n → ∞} = 1, т. е. P{
P
n−1
k=0
τ
k
→
∞, n → ∞} = 1.
Доказательство того, что процесс ξ(t) — цепь Маркова, сложнее.
Лемма 7.1. Если события B
1
, B
2
, . . . попарно не пересекаются (B
i
∩B
j
= ∅ при
i 6= j) и событие A удовлетворяет условиям P{A |B
i
} = p, i = 1, 2, . . . , то
P
(
A
¯
¯
¯
¯
¯
[
i>1
B
i
)
= p.
Доказательство. Так как P{A |B
i
} = p, то P{AB
i
} = pP{B
i
}. Так как события
B
i
попарно не пересекаются, то
P
(
A
¯
¯
¯
¯
¯
[
i>1
B
i
)
=
P {A ∩ (∪
i>1
B
i
)}
P {∪
i>1
B
i
}
=
P
i>1
P{AB
i
}
P
i>1
P{B
i
}
=
P
i>1
pP{B
i
}
P
i>1
P{B
i
}
= p.
Замечание. Для пересекающихся событий B
i
утверждение леммы может не
выполняться. Например, если P{B
1
} = P{B
2
} > 0, то при A = B
1
∩B
2
, 0 < P{A} <
P{B
1
},
P{A|B
1
∪ B
2
} =
P{A}
P{B
1
} + P{B
2
} − P{A}
<
P{A}
P{B
1
}
= P{A|B
1
} = P{A|B
2
}.
Теперь проверим наличие марковского свойства. Чтобы вычислить
P{ξ(t
n
) = i
n
|ξ(t
n−1
) = i
n−1
, . . . , ξ(t
0
) = i
0
},
разобьем событие в условии на непересекающиеся события
B
k
= {ξ(t
n−1
) = i
n−1
, . . . , ξ(t
0
) = i
0
, T
k
6 t
n−1
< T
k+1
}, k = 0, 1, . . .
В силу свойства 2 показательного распределения при любом y ∈ (0, t
n−1
)
P{T
k+1
− t
n−1
> x|T
k
= t
n−1
− y, B
k
} = e
−λ
i
n−1
x
.
Если выполняется событие B
k
, то ξ(t
n−1
) = i
n−1
= ξ
k
; согласно определению (28) и
формуле полной вероятности
P{T
k+1
− t
n−1
> x|B
k
} =
=
t
n−1
Z
0
P{T
k+1
− t
n−1
> x|T
k
= t
n−1
− y, B
k
}dP{T
k
6 y} = e
−λ
i
n−1
x
,
44
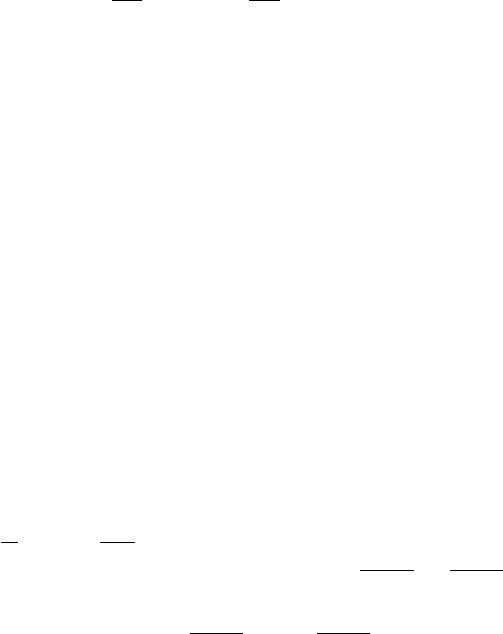
поскольку подынтегральная функция — константа. Далее, траектория ξ(t) при t >
t
n−1
и фиксированных значениях t
n−1
и i
n−1
полностью определяется:
а) последовательностью будущих состояний ξ
k
= i
n−1
, ξ
k+1
, . . ., не зависящей (при
фиксированном i
n−1
) от ξ
0
, . . . , ξ
k−1
, от τ
0
, . . . , τ
k−1
и от t
n
− T
k
,
б) случайными величинами τ
k+1
, τ
k+2
, . . . (определяющими времена пребывания в
состояниях), не зависящими от τ
0
, . . . , τ
k−1
, t
n−1
− T
k
= t
n−1
− (τ
0
+ . . . + τ
k−1
) и от
ξ
0
, . . . , ξ
k−1
,
в) остаточным временем пребывания в состоянии i
k−1
T
k+1
− t
n−1
=
k
X
j=0
τ
j
λ
ξ
j
− t
n−1
=
τ
k
λ
ξ
k
− (t
n−1
− T
k
),
не зависящим от t
n−1
− T
k
, τ
0
, . . . , τ
k−1
и от ξ
0
, . . . , ξ
k−1
.
Поэтому при любом k = 0, 1, . . .
P{ξ(t
n
) = i
n
|B
k
} = P{ξ(t
n
) = i
n
|ξ(t
n−1
) = i
n−1
} = p
i
n−1
i
n
(t
n
− t
n−1
).
Отсюда и из леммы следует, что
P{ξ(t
n
) = i
n
|ξ(t
n−1
) = i
n−1
, . . . , ξ(t
0
) = i
0
} = P{ξ(t
n
) = i
n
|ξ(t
n−1
) = i
n−1
}.
Тем самым утверждение 7.1 доказано.
Цепи Маркова, число переходов которых на любом конечном отрезке времени
конечно с вероятностью 1, называются регулярными. Утверждение 2 содержит
довольно грубые достаточные условия, обеспечивающие регулярность цепи Маркова
с непрерывным временем.
Пример 7.1: нерегулярная цепь Маркова. Пусть цепm ξ(t) имеет
детерминированную вложенную цепь Маркова {ξ
k
}: ξ
k
= k, k = 0, 1, . . ., и
λ
k
= (k + 1)
2
, k ≥ 0. Обозначим через θ
k
время первого попадания цепи ξ(t) в
состояние k, т.е. θ
k
= τ
0
+
τ
1
2
2
+ . . . +
τ
k−1
k
2
. Последовательность θ
k
при k ↑ ∞ монотонно
возрастает, поэтому существует lim
k→∞
θ
k
= θ
∗
. Так как M
τ
n
(n+1)
2
=
1
(n+1)
2
, то
Mθ
∗
= lim
k→∞
Mθ
k
=
X
k>0
M
τ
k
(k+1)
2
=
X
k>0
1
(k+1)
2
< ∞.
Следовательно, P{θ
∗
< ∞} < 1, т.е. траектория цепи ξ(t) с вероятностью 1 совершает
бесконечное число переходов за конечное время.
Существуют регулярные счетные цепи Маркова, для которых множество Λ
интенсивностей выхода не ограничено (но тогда матрицы вероятностей переходов
в моменты скачков должны удовлетворять некоторым условиям). Очевидно, любая
цепь Маркова с конечным множеством состояний регулярна.
Замечание. Структура траекторий неоднородных по времени цепей Маркова с
непрерывным временем сложнее; времена пребывания в состояниях таких цепей,
вообще говоря, имеют распределения, отличные от показательных и могут быть
зависимыми (несмотря на наличие марковского свойства условной независимости
будущего от прошлого при фиксированном настоящем).
45

Для цепей Маркова с непрерывным временем определяются переходные
вероятности
p
ij
(t) = P{ξ(s + t) = j|ξ(s) = i}.
При любом t ≥ 0 набор kp
ij
(t)k
i,j∈S
образует матрицу вероятностей переходов P (t).
Лемма 7.2. Если ξ(t) — однородная цепь Маркова с непрерывным временем и
не более чем счетным множеством состояний S, а P (t) — матрица вероятностей
переходов за время t, то для любых t, s > 0
P (t + s) = P (t)P (s).
Доказательство. Пользуясь формулой полной вероятности и тем, что множество
состояний S не более чем счетно, а вероятностные меры счетно аддитивны, находим,
что при любых i, j ∈ S
p
ij
(t + s) = P{ξ(s + t) = j|ξ(0) = i} =
=
X
k∈S
P{ξ(t) = k|ξ(0) = i}P{ξ(s + t) = j|ξ(t) = k} =
=
X
k∈S
P{ξ(t) = k|ξ(0) = i}P{ξ(s) = j|ξ(0) = k} =
X
k∈S
p
ik
(t)p
kj
(s).
Это равенство означает, что (P (t + s))
ij
= (P (s)P (t))
ij
для любых i, j ∈ S. Лемма
доказана.
Если ξ(t) — однородная цепь Маркова с непрерывным временем, то из леммы
7.2 следует, что при любом h > 0 последовательность {ξ(nh), n = 0, 1, . . .} образует
цепь Маркова с матрицей вероятностей переходов P (h), и, значит, P (nh) = ( P (h))
n
при любых h > 0 и натуральных n. В частности, P (1) = (P (
1
n
))
n
. Вообще, семейство
P (t), t > 0, образует коммутативную полугруппу по умножению. Цепь {ξ(nh)} тоже
называют цепью, вложенной в цепь ξ(t) с непрерывным временем).
Лемма 7.3. Пусть ξ(t) — однородная цепь Маркова с непрерывным временем
и не более чем счетным множеством состояний S, с вложенной цепью Маркова
ξ
n
, имеющей матрицу вероятностей переходов в моменты скачков kp
ij
k, и с
интенсивностями выходов λ
i
< ∞. Если состояние j вложенной цепи ξ
n
следует
за состоянием i, то p
ij
(t) > 0 при всех t > 0.
Доказательство. Если состояние j следует за состоянием i, то существуют такие
k < ∞ и состояния i
1
, . . . , i
k
, что
p
ii
1
p
i
1
i
2
. . . p
i
k−1
i
k
p
i
k
j
> 0.
Пусть τ
0
, τ
1
, . . . — независимые случайные величины, имеющие показательное
распределение с параметром 1. Тогда время перехода цепи ξ(t) по цепочке ii
1
. . . i
k
j
из состояния i в состояние j имеет такое же распределение, как сумма
σ =
τ
0
λ
i
+
τ
1
λ
i
1
+ . . . +
τ
k−1
λ
i
k−1
+
τ
k
λ
i
k
,
46

а время пребывания в состоянии j — как случайная величина τ
k+1
/λ
j
. Вероятность
перехода из состояния i в состояние j за время t не меньше вероятности того, что
этот переход пройдет по цепочке состояний ii
1
. . . i
k
j за случайное время σ < t, а
после попадания в состояние j цепь не совершит ни одного перехода до момента t.
Поэтому для любого t > 0 справедлива оценка
p
ij
(t) = P{ξ(t) = j|ξ(0) = i} > p
ii
1
p
i
1
i
2
. . . p
i
k−1
i
k
p
i
k
j
P
n
σ < t < σ +
τ
k+1
λ
j
o
.
Распределение случайной величины σ как распределение суммы независимых
случайных величин, имеющих показательные распределения, имеет положительную
плотность f на всей положительной полуоси.
Поэтому
P
n
σ < t < σ +
τ
k+1
λ
j
o
=
Z
t
0
f(x)P
n
τ
k+1
λ
j
> t − x
o
dx > 0.
Лемма доказана.
Теорема 7.1. Пусть ξ(t) — однородная цепь Маркова с непрерывным временем
и конечным множеством состояний {1, . . . , N} и с интенсивностями выходов λ
i
<
∞. Если все состояния вложенной цепи Маркова ξ
n
сообщаются, то при любых
i, j ∈ S существуют положительные пределы
lim
t→∞
p
ij
(t) = p
j
, j ∈ {1, . . . , N}, (29)
не зависящие от начального состояния i.
Доказательство. Согласно лемме 7.2 случайная последовательность {ξ(n), n =
0, 1, . . .} образует цепь Маркова с дискретным временем и матрицей вероятностей
переходов P (1). Согласно лемме 7.3 все элементы матрицы P (1) положительны.
Следовательно, при любом i существуют пределы
lim
n→∞
P{ξ(n) = j|ξ(0) = i} = p
j
, j = 1, . . . , N, (30)
не зависящие от i, и вектор (p
1
, . . . , p
N
) ∈ G
N
является собственным для матрицы
P (1).
Аналогично для любого x > 0 последовательность {ξ(x+n), n = 0, 1, . . .} образует
конечную цепь Маркова с той же переходной матрицей P (1), т. е. при любом x и
любом i существуют те же самые пределы
lim
n→∞
P{ξ(x + n) = j|ξ(x) = i} = p
j
, j = 1, . . . , N. (31)
Так как G
N
— компакт и скорость сходимости в (30) и (31) одна и та же, то из (30)
и (31) следует, что для всех i ∈ {1, . . . , N } существуют
lim
t→∞
P{ξ(t) = j|ξ(0) = i} = p
j
, j = 1, . . . , N.
Тем самым теорема доказана.
47
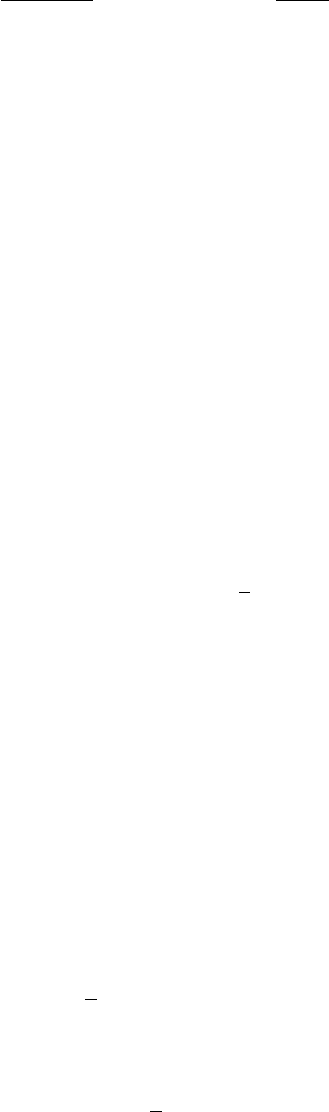
Теорема 7.2. Пусть ξ(t) — однородная по времени цепь Маркова с непрерывным
временем, которая имеет не более чем счетное множество состояний S,
вложенную цепь Маркова ξ
n
, матрицу вероятностей переходов в моменты скачков
kp
ij
k, p
ii
≡ 0, и интенсивности выходов λ
i
∈ (0, ∞), sup
i∈S
λ
i
= λ
∗
< ∞. Тогда для
переходных вероятностей p
ij
(t) существуют пределы
q
i
= lim
t↓0
1 − p
ii
(t)
t
= λ
i
, q
ij
= lim
t↓0
p
ij
(t)
t
= λ
i
p
ij
, i, j ∈ S.
Доказательство. Пусть ξ(0) = i, тогда τ
i
= inf{t : ξ(t) 6= i} имеет показательное
распределение с параметром λ
i
:
P{τ
i
> x} = e
−λ
i
x
, x ≥ 0. (32)
Поэтому по формуле полной вероятности по значению момента первого выхода
цепи ξ(t) из состояния i
e
−λ
i
t
= P{τ
i
> t} 6 p
ii
(t) = P{τ
i
> t} +
Z
t
0
X
j∈S\i
p
ij
p
ji
(t − u)dP{τ
i
6 u} 6
6 e
−λ
i
t
+
Z
t
0
X
j∈S\i
p
ij
P{τ
j
6 t − u}dP{τ
i
6 u},
поскольку p
ji
(t − u) 6 P{τ
j
6 t − u}.
Из (32) следует, что
Z
t
0
X
j
p
ij
P{τ
j
6 t − u}dP{τ
i
6 u} =
Z
t
0
X
j
p
ij
(1 − e
−λ
j
(t−u)
)λ
i
e
−λ
i
u
du 6
6
Z
t
0
X
j
p
ij
λ
j
(t − u)λ
i
du 6
1
2
t
2
λ
i
λ
∗
= o(t
2
), t → 0.
Значит,
1 − p
ii
(t) = 1 − e
−λ
i
t
+ o(t
2
) = λ
i
t + o(t), t → 0;
что доказывает первое утверждение теоремы.
Для доказательства второго утверждения заметим, что при любом j 6= i
p
ij
(t) >
Z
t
0
p
ij
P{τ
j
> t − u}dP{τ
i
6 u} =
= p
ij
Z
t
0
e
−λ
j
(t−u)
λ
i
e
−λ
i
u
du = λ
i
p
ij
t(1 + o(1)), t → 0.
Из этих неравенств следует, что
lim inf
t↓0
1
t
p
ij
(t) > λ
i
p
ij
при всех j 6= i,
и, поскольку по условию p
ii
= 0,
X
i6=j
lim inf
t↓0
1
t
p
ij
(t) >
X
i6=j
λ
i
p
ij
= λ
i
. (33)
48

Ранее мы доказали, что при λ
∗
< ∞ число скачков цепи Маркова на любом
конечном отрезке времени конечно с вероятностью 1, т. е.
P
j
p
ij
(t) = 1 для любого
t > 0. Таким образом,
X
j6=i
p
ij
(t) = 1 − p
ii
(t) 6 1 − e
−λ
i
t
и
lim sup
t↓0
X
j6=i
1
t
p
ij
(t) 6 lim sup
t↓0
1
t
(1 − p
ii
(t)) 6 lim
t↓0
1
t
(1 − e
−λ
i
t
) = λ
i
.
Объединяя последнюю оценку с (33), находим:
λ
i
6
X
j6=i
lim inf
t↓0
1
t
p
ij
(t) 6 lim inf
t↓0
X
j6=i
1
t
p
ij
(t) 6 lim sup
t↓0
X
j6=i
1
t
p
ij
(t) 6 λ
i
. (34)
Если существует такое v 6= i, что lim sup
t→0
1
t
p
iv
(t
k
) > λ
i
p
iv
, то (поскольку
P
j
p
ij
= 1)
λ
i
> lim sup
t↓0
X
j6=i
1
t
p
ij
(t) > λ
i
p
iv
+ lim inf
t↓0
X
j6=i,v
1
t
p
ij
(t) >
> λ
i
p
iv
+
X
j6=i,v
lim inf
t↓0
1
t
p
ij
(t) >
X
i6=j
λ
i
p
ij
= λ
i
,
что противоречит (34). Теорема доказана.
Утверждение теоремы 7.2 можно записать в матричном виде: существует
lim
t→+0
P (t) − P (0)
t
= Q = kq
ij
k,
где q
ii
= −q
i
и P (0) = E — единичная матрица. Матрица Q называется матрицей
интенсивностей переходов цепи Маркова с непрерывным временем.
С помощью теоремы 7.2 можно вывести уравнения для переходных вероятностей
цепи Маркова с непрерывным временем.
Теорема 7.3. При условиях теоремы 7.2 матрицы вероятностей переходов
цепи Маркова с непрерывным временем с матрицей интенсивностей переходов Q
удовлетворяют дифференциальным уравнениям
P
0
(t) = P (t)Q, (35)
P
0
(t) = QP (t). (36)
Решения этих систем имеют вид P (t) = e
Qt
, t ≥ 0, где
e
A
= E +
X
k≥1
1
k!
A
k
для квадратной матрицы A.
Доказательство. Из леммы 7.2 следует, что
P (t + s) − P (t) = P (t)(P (s) − P (0)) = (P (s) − P (0))P (t).
Отсюда, пользуясь теоремой 7.2, получаем:
P
0
(t) = lim
s→0
1
s
(P (t + s) − P (t)) = lim
s→0
1
s
P (t)(P (s) − P (0)) = P (t)Q.
49

Справедливость уравнения (36) устанавливается аналогично, так как
мультипликативная полугруппа матриц {P (t)} коммутативна.
Из уравнения (35) следует, что функция P (t) бесконечно дифференцируема и
что P
(k)
(t) = P (t)Q
k
, k = 1, 2, . . . Разлагая эту функцию в ряд Тейлора в точке 0,
находим:
P (t) = P (0) +
∞
X
k=1
1
k!
P
(k)
(0)t
k
=
∞
X
k=0
1
k!
Q
k
t
k
= e
Qt
.
Теорема доказана.
Уравнение (35) называется обратным уравнением Колмогорова, а уравнение (36)
— прямым уравнением Колмогорова.
8. Условные математические ожидания
Пусть (Ω, F, P) — вероятностное пространство и B = {B
1
, B
2
, . . .} — измеримое
разбиение Ω на множества положительной меры. (Далее все разбиения мы будем
предполагать измеримыми, не оговаривая этого специально.) Тогда для каждого
события C определены условные вероятности P{C|B
k
} =
P{C∩B
k
}
P{B
k
}
, k = 1, 2, . . .
Случайная величина
ξ
B
= ξ
B
(ω) =
X
k≥1
P{C|B
k
}χ
B
k
(ω) = P{C|B}.
называется условной вероятностью события C относительно разбиения B. На
каждом множестве B
k
она принимает постоянное значение P{C|B
k
}.
Если разбиение B порождается случайной величиной η, то говорят об условной
вероятности относительно случайной величины η или относительно порожденной
ею σ-алгебры σ(η):
P{C|η} = P{C|σ(η)} = P{C|η}(ω).
Замечание. Так как случайная величина η на каждом элементе порожденного
ею разбиения постоянна, то условную вероятность P{C|η} = P{C|σ(η)} можно
представить в виде функции от C и η:
P{C|η}(ω) = p(C, η(ω)).
Рассмотрим теперь аналогичную конструкцию для случайных величин. Пусть
на вероятностном пространстве (Ω, F, P) заданы: разбиение B = {B
1
, B
2
, . . .} и
случайная величина ξ с конечным или счетным множеством значений x
1
, x
2
, . . . ∈ R,
порождающая разбиение A = {A
1
, A
2
, . . .} пространства Ω на непересекающиеся
множества A
k
= {ω ∈ Ω : ξ(ω) = x
k
} ∈ F, k ≥ 1.
Условные вероятности
P{A
k
|B} = P{A
k
|B}(ω) = P{ξ = x
k
|B}(ω), ω ∈ Ω,
определены для всех k ≥ 1, и для каждого ω ∈ Ω они образуют вероятностное
распределение на множестве {x
1
, x
2
, . . .} значений ξ, зависящее от ω. Определим
50
