Золотаревский В.С. Механические свойства металлов
Подождите немного. Документ загружается.


речного
скольжения
винтовых
дислокаций.
Уровень
напряжений, достаточный
для
интенсивного
попе
речного
скольжения
винтовых
дислокаций,
достигается
в
точке
с
(рис.
27).
За
счет
обхода
барьеров
степень
упрочнения
на
третьей
стадии
(участок
ck)
становится
меньше,
чем
на
второй.
При
этом
с
увеличением
степени
деформации
dt/
dg
уменьшается,
так
как
рост
напряжений
выше
t
c
'
все
больше
облегчает
обход
барьеров
за
счет
поперечного
скольжения
-
идет
так
называемый
динами
ческий
возврат.
Механизм
фрагментации
полос
скольжения
в
результате
этого
же
процесса
можно
представить
следующим
образом.
Дислока
ции,
обошедшие
барьеры,
переходят
в
«свободные»
плоскости
и
скользят
в
них,
пока
не
выйдут
на
поверхность.
Естественно,
что
не
все
заторможенные
дислокации
способны
обойти
барьеры
и
не
все
плоскости,
в
которые
они
могут
перейти,
свободны
от
других
барьеров
и
позволят
дислокациям
дойти
до
поверхности.
В
результате
происходит
увеличение
плотности
линий
скольжения
внутри
отдельных
участков
полос,
в
то
время
как
другие
остают
ся
неизменными.
Внешне
это
и
проявляется
как
фрагментация
полос
скольжения
(см.
рис.
29,
г).
Стадия
множественного
скольжения
и
последняя
стадия
ин
тенсивно
развитого
поперечного
скольжения
у
многих
металлов
силь
но
перекрываются,
т.е.
поперечное
скольжение
может
наблюдаться
уже
в
начале
множественного
скольжения.
Понятно,
что
во
всех
случаях
на стадии
интенсивно
развитого
поперечного
скольже
ния
движение
дислокаций
идет
в
нескольких
системах
и,
следо
вательно,
здесь
мы
тоже
имеем
дело
с
множественным
скольже
нием.
Как
видно
из
схемы
на
рис.
20,
а,
по мере
деформации
в
f<ри
сталле
происходит
поворот
плоскости
(и
направления)
скольже
ния
в
сторону
приближения
к
оси
растяжения.
После
значитель
ного
удлинения
(на
десятки
процентов)
в
кристалле
возникает
определенная
текстура
деформации.
Сближение
направления
скольжения
с
осью
растяжения
имеет
очень
большое
значение,
так
как
при
водит
к
изменению
величины
касательных
напряже
ний
в
действующей
системе
скольжения
и
является
одной
из
при
чин
начала
движения
дислокаций
в
других
системах.
Итак,
на
качественном
уровне
мы
объяснили
трехстадийность
пластической
деформации
г.
ц.
к.-монокристаллов
и
кривых
их
деформационного
упрочнения
(рис.
27).
Для
более
детального
ана-
60

лиза
деформационного
упрочнения
необходимо
рассмотреть
воз
можные
причины
торможения
дислокаций
и
оценить
их
вклад
в
упрочнение
на
разных
стадиях
деформации.
В
монокристаллах
чистых
металлов
дислокации
тормозятся
за
счет
силы
трения
решетки,
упругого
взаимодействия
с
другими
дислокациями,
образования
ступенек
(порогов)
при
пересече
нии
дислокаций
и
за
счет
образования
точечных
дефектов,
обра
зующихся
при
движении
дислокаций спорогами.
Сила
трения
решетки,
препятствующая
скольжению
дислока
ций
в
отсутствие
каких-либо
дефектов,
в
чистых
монокристаллах
должна
быть
близка
по
величине
к
силе
Пайерлса
-
Набарро:
2G
t
п
-
н
=
--е
l-v
Ь
1 - v
2л
а
(25)
где
а
-
расстояние
между
соседними
плоскостями,
по
которым
идет
скольжение
(в
последине
годы
часто
трактуется
как
ширина
дислокации);
Ь
-
межатомное
расстояние
в
направлении
сколь
жения;
v -
коэффициент
Пуассона.
Расчетные
значения
(п-и
значительно
меньше
эксперименталь
ных
значений
(КР.
Поэтому
сила
Пайерлса
-
Набарро
не
должна
вносить
существенного
вклада
в
деформационное
упрочнение
г.
ц.
к.
металлов.
Следует
отметить
несовершенство
существующих
рас
четных
методов
оценки
этой силы,
так
что
ее
истинное
значение
может
оказаться
более
весомым.
Торможение
за
счет
упругого
взаимодействия
между
дислока
циями
является,
по-видимому,
основным
механизмом
деформа
ционного
упрочнения.
Оно
проявляется
уже
при
встрече
скользя
щих
дислокаций
с
дислокациями
«леса»,
пересекающими
плос
кость
скольжения.
Чем
больше
плотность
дислокаций
леса,
тем
труднее
перемещаться
скользящим
дислокациям.
Еще
более
зна
чителен
результат
упругого
взаимодействия
дислокаций,
останов
ленных
различными
барьерами:
сидячими
дислокациями,
в
част
ности
барьерами
Ломер
-
Коттрелла
в
г.
ц.
к.
решетке,
диполями,
дислокационными
сплетениями
или
границами
и
т.д.
Таким
ре
зультатом
является
образование
дислокационных
скоплений,
об
ратное
поле
упругих
напряжений
от
которых
постепенно
запира
ет
источники
дислокаций,
затрудняя
продолжение
деформации.
Большинство
теорий
деформационного
упрочнения,
в
част
ности
г.
ц.
к.
металлов,
базируется
на
эффекте
упругого
взаимо-
61

действия
между
дислокациями.
Эти
теории,
исходя
из
ряда
упро
щающих
предпосылок,
часто
основанных
на
экспериментальных
данных
структурного
анализа,
позволяют
получать
уравнения
связи
напряжения
с
деформацией.
Такие
уравнения
можно
сопостав
лять
с
экспериментальными
кривыми,
проверяя
обоснованность
используемых
теорией
положений.
Рассмотрим
в
качестве
приме
ра
выводы
одной
из
первых
теорий
упрочнения
за
счет
полей
дальнодействующих
упругих
напряжений,
предложенной
Тейло
ром.
Величина
напряжения
на
каком-то
расстоянии
r
от
дислока
ции
убывает
по
закону
(=
а
Gb/(2тtr)
,
где
Ь
-
вектор
Бюргерса;
а
-
постоянная,
зависящая
от
типа
дислокации.
Для
винтовой
дислокации
а:::::
1,
для
краевой
-
3/2.
Допустим,
что
а
=
1.
Если
дислокаций
много
и
они
беспорядочно
распреде
лены
по
кристаллу,
то
результирующее
напряжение,
действую
щее
на
какую-то
одну
дислокацию
со
стороны
всех
остальных,
будет
(,
=
Gb/(2тt'ep)'
где
'ер
-
среднее
расстояние
между
дислокациями.
Величина
'ер
определяется
плотностью
дислокаций
р:
, = 1 /
.J
p
.
ер
Следовательно,
t,=Gb.Jp
/
2тt.
Для
перемещения
дислокации
на
заметное
расстояние
необ
ходимо
приложить
внешнее
напряжение,
по крайней мере
рав
ное
внутреннему
напряжению
11.
Представим
себе
теперь,
что
каждая
дислокация
перемещается
на
определенное
расстояние
L,
а
затем
больше
не
двигается
и
L
не
меняется
в
процессе
де
формации.
Тогда,
учитывая,
что
из
уравнения
(23)
плотность
дис
локаций
р
= g/bL,
получим
1\
=
(Gb
/
2тt)Jg
/
bL,
(26)
т.е.
параболическую
зависимость
напряжения
от
деформации.
62

Такой
вывод
не
согласуется
с
общим
видом
эксперименталь
ной
кривой
растяжения
благоприятно
ориентированного
крис
талла
(см.
рис.
27).
Уравнение
(26)
соответствует
только
закону
изменения
t
от
g
на
111
стадии
деформационного
упрочнения.
Для
объяснения
деформационного
упрочнения
на
1
и
11
стадиях
на
основе
теории
дальнодействующих
напряжений
приходится
вво
дить
новые
допущения.
Например,
по
Зегеру
на
стадии
легкого
скольжения
в
единице
объема
кристалла
содержится
определен
ное
и
неизменное
число
дислокационных
источников
N,
каждый
из
которых
испускает
при
заданном
напряжении
определенное
число
дислокационных
петель
и
средняя
длина.
линии
скольже
ния
L
постоянна.
Рост
напряжения
dt
является
результатом
увеличения
числа
петель
на
dn.
Соответствующий
прирост
деформации
происходит
на
величину
dg=bNL
2
dn.
Число
источников
N
можно
выразить
через
L
и
расстояние
между
дислокационными
петлями
1:
и
тогда
dg=
bdn/l.
(27)
в
результате
возникновения
dn
новых
дислокационных
петель
возрастет
и
обратное
напряжение
t
об
,
действующее
на
дислока
ционные
источники:
dt
обр
= Gbdn/(2rrL).
(28)
Когда
dt
обр
=
dt,
генерация
новых
петель
источниками
прекра
тится.
Из
выражений
(27)
и
(28)
получаем
dt
(1)
=
~(l
/
L).
dg
2п
(29)
Более
точный
анализ
приводит
к
близкому
уравнению
dt
(1)
= 8G
(1
/
L)З/4.
dg
9п
(30)
63

Показано,
что
для
меди
[::::
30
нм,
а
L::::
600
мкм.
Тогда
получа
ется,
что
расчетный
коэффициент
деформационного
упрочне
ния
на
1
стадии
-7,5
МПа
очень
близок
к
экспериментально
на
блюдаемому
(7,0
МПа).
Для
II
стадии
Зегер
использует
те
же
предпосылки
плюс
обра
зование
плоских
дислокационных
скоплений
у
барьеров
Ломер
-
Коттрелла
по трем
плотноупакованным
направлениям
в
плоско
сти
скольжения.
Предполагается,
что
упрочнение
является
резуль
татом
дальнодействующих
напряжений
от
этих
скоплений,
кото
рые
взаимодействуют
между
собой.
Если каждое скопление
состоит
из
n
дислокаций,
число
скоп
лений
в
единице
объема
N,
а
длина
пути
перемещения
дислока
ций
принимается
постоянной
(L),
то
величина
произведенной
деформации
g =
NnL2
n
b.
Группы
дислокаций
в
скоплениях,
находящихся
друг
от
друга
на
расстоянии
[::::
1/(2NL)I/2,
принимаются
за
сверхдислокации
при
расчете
напряжений.
Тогда
для
перемещения
дислокаций
через
возникшее
поле
внутренних
напряжений
с
учетом
(28)
необходимо
приложить
внешнее
на
пряжение
t = Gbn/(2n/).
Число
дислокаций
в
скоплениях
n = 2ntL/
bG.
Из
приведенных
уравнений
следует,
что
t/gG = const.
По
экспериментальным
данным,
длина
линий
скольжения
обратно
пропорциональна
сдвиговой
деформации
на
11
стадии:
L =
A/(g-g),
где
g'
-
деформация
в
конце
1
стадии;
А
-
константа.
В
результате
коэффициент
деформационного
упрочнения
на
11
стадии
по
Зегеру
64

dt
pG
-(II)~-.
dg
6л
2
(ЗI)
Принимая
постоянную
Р
= 0,5,
получаем
неплохое
соответ
ствие
с
экспериментальными
данными.
Некоторые
теории
объясняют·
деформационное
упрочнение
полями
близкодействующих
напряжений.
Например,
по
Гилману
основной
причиной
деформационного
упрочнения
является
об
разование
дислокационных
диполей
при
движении
винтовых
или
смешанных
дислокаций
с
порогами.
После
отрыва
диполя
от
сколь
зящей
дислокации
он
остается
в
плоскости
скольжения
и пре
пятствует
перемешению
других
дислокаций,
скользящих
вслед
за
той,
от
которой
он
оторвался.
Чем
больше
степень
деформации,
тем
больше
таких
диполей
и
тем
выше
должно
быть
напряжение,
необходимое
для
продолжения
деформации.
Другая
теория
упрочнения
полями
близкодействующих
напря
жений,
предложенная
Кульман-
Вильсдорф,
базируется
на
обра
зовании
дислокационных
сплетений.
Эта
теория
учитывает
экс
периментальный
факт
частого
образования
при
деформации
яче
истой
дислокационной
структуры
(см.
рис.
ЗО,
г).
По
Кульман
Вильсдорф
на
стадии
легкого
скольжения
происходит
постепен
ное
заполнение
кристалла
дислокациями,
которые
распределя
ются
неравномерно.
К
началу
11
стадии
дислокации
имеются
уже
во
всех
ранее
свободных
областях
кристалла.
Они
образуют
спле
тения,
внутри
которых
плотность
дислокаций
выше,
чем
в
про
межутках
между
ними.
На
стадии
множественного
скольжения
плотность
дислокаций
продолжает
расти,
при
этом
расстояние
между
скоплениями
уменьшается
по
мере
деформации.
Прогрес
сирующее
упрочнение
объясняется
здесь
уменьшением
длины
источников
Франка-Рида:
с
повышением
плотности
дислока
ций
расстояние
между
ними
уменьшается
и,
следовательно,
ста
новятся
короче
отрезки
дислокаций,
которые
могут
изгибаться,
генерируя
новые
петли.
Напряжение,
необходимое
для
начала
ра
боты
источника,
обратно
пропорционально
его
длине.
Таким
об
разом,
для
продолжения
деформации
требуется
непрерывное
повышение
внешнего
напряжения,
особенно
на
11
стадии.
Умень
шение
коэффициента
деформационного
упрочнения
на
111
ста
дии,
как
и
в
других
теориях,
объясняют
интенсивным
попереч
ным
скольжением,
способствующим,
в
частности,
аннигиляции
дислокаций.
3 - 3755
65

К
теориям
упрочнения
близкодействующими
полями
упругих
напряжений
примыкают
теории,
связывающие
деформационное
упрочнение
с
торможением
дислокаций
из-за
образования
на
них
порогов
в
результате
взаимного
пересечения.
Как
известно,
дис
локациям
с
порогами
(ступеньками)
скользить
труднее,
чем
без
порогов.
Особенно
это
относится
к
винтовым
дислокациям,
по
роги
на
которых
имеют
краевую
ориентацию.
При
движении
этих
дислокаций
образуются
диполи,
а
также
цепочки
вакансий
или
межузельных
атомов,
которые
затрудняют
движение
других
дис
локаций
(теория
Гилмана).
Вклад
порогов
в
торможение
дислока
ций,
на
которых
они
образовались,
можно
оценить
количествен
но:
t =
aCb//'~
(32)
где
/' -
расстояние
между
порогами.
По
мере
деформации
l'
уменьшается
и
действующее
напряже
ние
t
должно
расти.
Уравнение
(32)
можно
получить,
приравни
вая работу,
совершаемую
дислокацией
при
ее
перемещении
на
расстояние
Ь
за
счет
внешней
силы
IJ2t,
к
затрате
энергии
на
об
разование
точечных
дефектов
при
скольжении
дислокаций
с
по
рогами
(aGb
3
/1),
где
а
-
коэффициент,
равный
-1
в
случае
обра
зования
межузельного
атома
и
-0,2
при
образовании
вакансии).
Анализ
причин
торможения
дислокаций
в
чистых
монокрис
таллах
показывает,
что
каждая
из
них
может
вносить
свой
вклад
в
наблюдаемое
деформационное
упрочнение.
Существующие
тео
рии
деформационного
упрочнения
исходят
обычно
лишь
из
ка
кой-либо
одной
причины
торможения.
Кроме
того,
эти
теории
используют
допущения,
заметно
упрошающие
реальную
слож
ную
картину
пластической
деформации.
Именно
сложность,
мно
гообразие
процессов,
сопровождаюших
деформационное
упроч
нение,
до
сих
пор
не
позволили
создать
общей
теории
упрочне
ния
даже
для
металлов
с
одной
решеткой.
Рассмотренные
в
качестве
при
мера
.
теории
разрабатывались
применительно
к
г.
ц.
к.
металлам.
Несмотря
на
все
свои
недостат
ки
и
противоречия,
они
позволяют
сделать
ряд
важных
общих
выводов.
На
стадии
легкого
скольжения
малый
коэффициент
деформа
ционного
упрочнения
есть
результат
движения
дислокаций
пре
имущественно
в
одной
системе.
При
малой
плотности
исходных
дислокаций
количество
барьеров,
величина
полей
упругих
на-
66

пряжений;
число
порorов на
дислокациях
и
т.д.
относительно
малы
и
слабо
увеличиваются
по
мере
деформации.
На
стадии
множественного
скольжения
резко
возрастает
плот
ность
дислокаций,
число
их
пересечений
и,
как
результат,
число
барьеров,
мощность
скоплений
и
сплетений,
число
порогов,
т.е.
тех
факторов,
которые
способствуют
увеличению
коэффициента
деформационного
упрочнения.
Большинство
теорий
деформационного
упрочнения
посвяще
ны
анализу
именно
II
стадии,
где
картина
пластической
дефор
мации
особенно
сложна.
Здесь
действуют
все
возможные
меха
низмы
торможения,
но
главным,
по-видимому,
все-таки
являет
ся
образование
скоплений,
сплетений
и
упругое
взаимодействие
дислокаций
у
барьеров
(в
частности,
Ломер-Коттрелла),
в
ре
зультате
чего
запираются
дислокационные
источники,
и
продол
жение
деформации
требует
значительного
прироста
внешнего
напряжения.
При
напряжениях,
достаточных
для
начала
массового
попе
речного
скольжения
дислокаций,
начинается
111
стадия,
где
при
рода
деформационного
упрочнения
сейчас
более
понятна,
чем
на
двух
предьщущих.
К
моменту
начала
III
стадии
скольжение
во
всех
системах
затормаживается
различными
барьерами.
Как
бьuю
показано,
дальнейшая
деформация
осуществляется
за
счет
обхо
да
барьеров
винтовыми
дислокациями
путем
поперечного
сколь
жения
(при
низких
температурах).
После
начала
этого
процесса
коэффициент
упрочнения
уменьшается,
происходит
динамичес
кий
возврат.
Ему
способствуют
также
многочисленные
процессы
аннигиляции
дислокаций
из-за
возрастания
вероятности
встреч
разноименных
дислокаций
в
одной
плоскости.
Все
теории
деформационного
упрочнения
дают
качественно
аналогичную
зависимость
напряжения,
необходимого
для
про
должения
пластической
деформации
(напряжение
течения),
от
плотности
дислокаций:
t = a'GbJP,
(33)
где
а'
-
коэффициент
порядка
10-1,
зависящий
от
природы
ме
талла,
его
кристаллографической
ориентировки,
структуры
и
вкла
да
различных
механизмов
торможения
дислокаций
в
общее
уп
рочнение.
3"
67
Таким
образом,
характер
изменения:
плотности
дислокаций
по
мере
деформации
в
значительной
мере
определя:ет
вид
кривой
деформационного
упрочнения:.
Действительно,
относительно
не
большому
(на
1-2
поря:дка)
приросту
плотности
дислокаций
на
1
стадии
соответствует
малое
упрочнение,
а
резкому
(на
2-4
по
ря:дка)
увеличению
числа
дислокаций
в
результате
множествен
ного
скольжения:
-
существенное
усиление
деформационного
упрочнения.
На
111
стадии
плотность
дислокаций
увеличивается
уже
в
меньшей
степени
(обычно
в
пределах
одного
поря:дка)
и
деформационное
упрочнение
здесь
не
так
ярко
выражено,
как
на
11
стадии.
Рассмотренные
элементы
механизма
пластической
деформа
ции
и
деформационного
упрочнения
Г.Ц.к.
монокристалла,
благо
приятно
ориентированного
для
одиночного
скольжения,
так
или
иначе
проявляются
при
растяжении
любых
других
образцов
из
металлов
с
этой и
другими
решетками.
Произвольно
ориентированные
монокристаллы
металлов
с
г.Ц.К.
решеткой
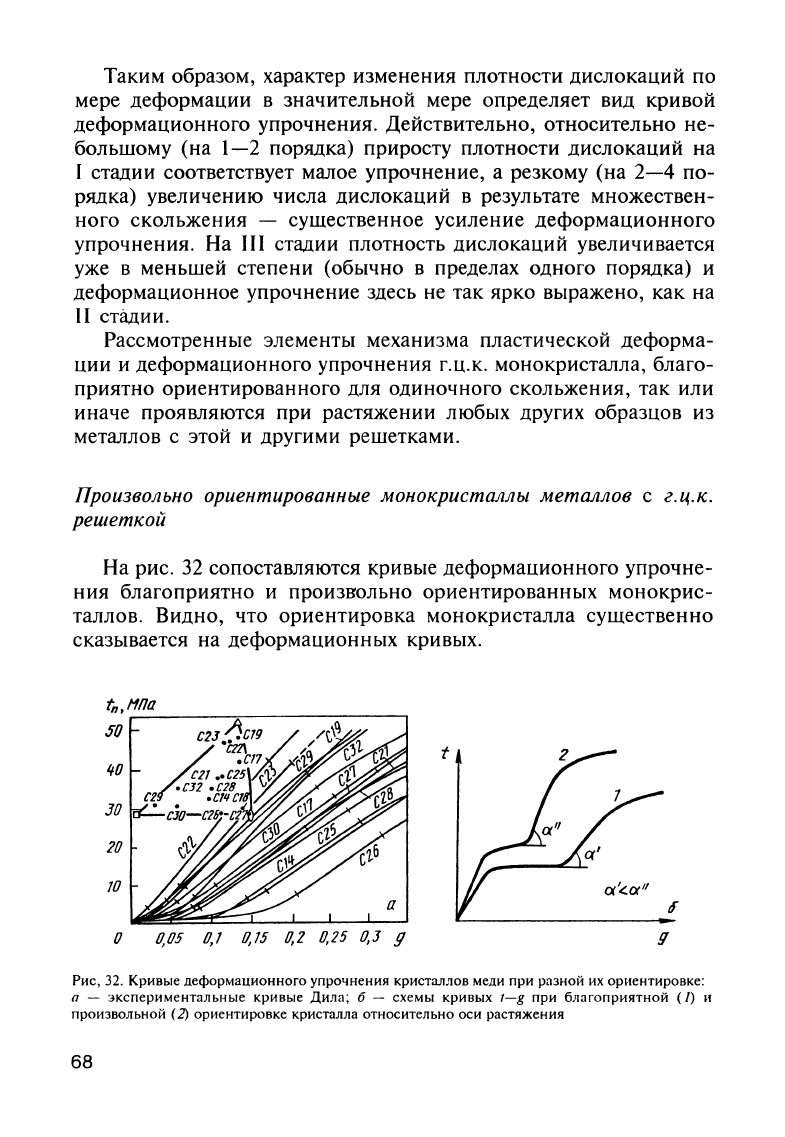
На
рис.
32
сопоставляются
кривые
деформационного
упрочне
ния
благоприятно
и
произвольно
ориентированных
монокрис
таллов.
Видно,
что
ориентировка
монокристалла
существенно
сказывается
на
деформационных
кривых.
tn.Hfla
$0
JO
20
10
О
0,05
0,1
0,15
9,2
0.25 0.3 9
t
!I
Рис,
32.
Кривые
деформаuионного
упрочнения
кристаллов
меди
при
разной
их
ориентировке:
а
-
экспериментальные
кривые
Дила; б
-
схемы
кривых
f-g
при
благоприятной
(1)
и
произвольной
(2)
ориентировке
кристалла
относительно оси
растяжения
68

При
произвольной
ориентировке
сокращается
или
совсем
ис
чезает
(если
с
самого
начала
величина
касательных
напряжений
хотя
бы
в
двух
системах
окажется
примерно
одинаковой)
стадия
легкого
скольжения,
увеличивается
коэффициент
упрочнения
на
1
и
11
стадиях,
растет
уровень
напряжений
течения.
Все
эти
раз
личия
максимальны
при
сравнении
«мягкой»
И
«твердой»
ориен
тировок
(см.
рис.
28).
«Мягкие»
ориентировки,
соответствующие
центральной
области
на
рис.
28,
находятся
далеко
от
сторон
стан
дартного
стереографического
треугольника,
особенно
от
сторо
ны
[001]-[1111,
к
котороЙ
в
процессе
деформирования
прибли
жается
ось
раст~жения.
В
кристаллах
с
такими
ориентировками
пластическая
деформация
начинается
(и
продолжается)
при
ми
нимальных
напряжениях
из-за
благоприятной
ориентировки
пер
вичной
системы
скольжения.
По
этой
же
причине
у
них
наблюда
ется
длинная
1
стадия
деформации.
«Твердые»
ориентировки
располагаются
вблизи
или
на грани
цах
стереографического
треугольника,
где
две
и
более
систем
скольжения
имеют
близкие
приведенные
напряжения
сдвига.
Поэтому
естественно,
что
на
кривых
деформационного
упрочне
ния
монокристаллов
с
такими
ориентировками
мы
видим
укоро
ченную
стадию
легкого
скольжения
и
более
сильный
прирост
напряжения
с
деформацией.
Это
иллюстрирует
на
примере
крис
талла
меди
рис.
32,
а.
Здесь
все
кривые
выходят
из
одной
точки,
поскольку
по
ординате
отложено
приведенное
напряжение
сдви
га.
Если
бы
по
вертикальной
оси
диаграммы
было
отложено
не
приведенное
(внешнее)
касательное
напряжение,
то
«твердым»
ориентировкам
соответствовали
бы
более
высокие
значения
на
пряжения
течения
от
начала
и
до
конца
пластической
деформа
ции
(см.
рис.
32, 6).
На
111
стадии
разница
в
коэффициентах
упрочнения
нивели
руется,
поскольку
к
концу
стадии
множественного
скольжения
возникает
дислокационная
структура,
уже
мало
зависящая
от
исходной
ориентировки
кристалла.
МонокрuстШlЛЫ
металлов
с
г.n.
решеткой
Рассмотрим
теперь
пластическую
деформацию
скольжением
металлов
с
г.п.
решеткой.
Наиболее
важным
отличием
г.п.
решет
ки
с
отношением
с/а
~
1,633
от
г.
ц.
к.
С
точки
зрения
деФормации
является
наличие
в
гексагональной
плотноупакованной
решетке
69
