Зимина О.В., Кириллов А.И., Сальникова Т.А. Высшая математика. Решебник

Подождите немного. Документ загружается.

340 Гл.

13.

Поверхностные интегралы

Так как da = г^ sinOdedip, имеем

27Г

7г/2

// f{x^y',z)d(7 = r^ d(f f {г

COS

if sine

у Г

simp

sinO,

Г COS 9)

sine de.

E 0 0

Вычисляем повторный интеграл и записываем ответ.

ПРИМЕР. ВЫЧИСЛИТЬ поверхностный интеграл

/А

где Е — верхняя полусфера

х^ +

2/^

+ г^ = 9, Z > 0.

РЕШЕНИЕ.

Вводим на заданной поверхности (сфере) криволинейные коор-

динаты

X = ^cos(^sin^,

у = ^sin(^sin^,

Z = QCOSO.

в этих координатах: поверхность задается условиями

i:= <

{д,в,^):

0<^<7г/2,

О < (^ < 27Г

Так как d

сг

= 9 sin

d(^

и /(ж, ?/) = ж^ + т/^ = 9 sin^ в, имеем

27Г

7г/2

Пх'^ + у^) da

I dip / 9sin^ (9-98^(9^(9.

Е 0 0

Вычисляем повторный интеграл:

27Г

7Г/2 7г/2

/d(^

А 9sin^ (9-9sin<9(i6> =-1627Г Ml - cos2<9) dcos(9 = ЮЗтг.

0 0 0

Ответ.

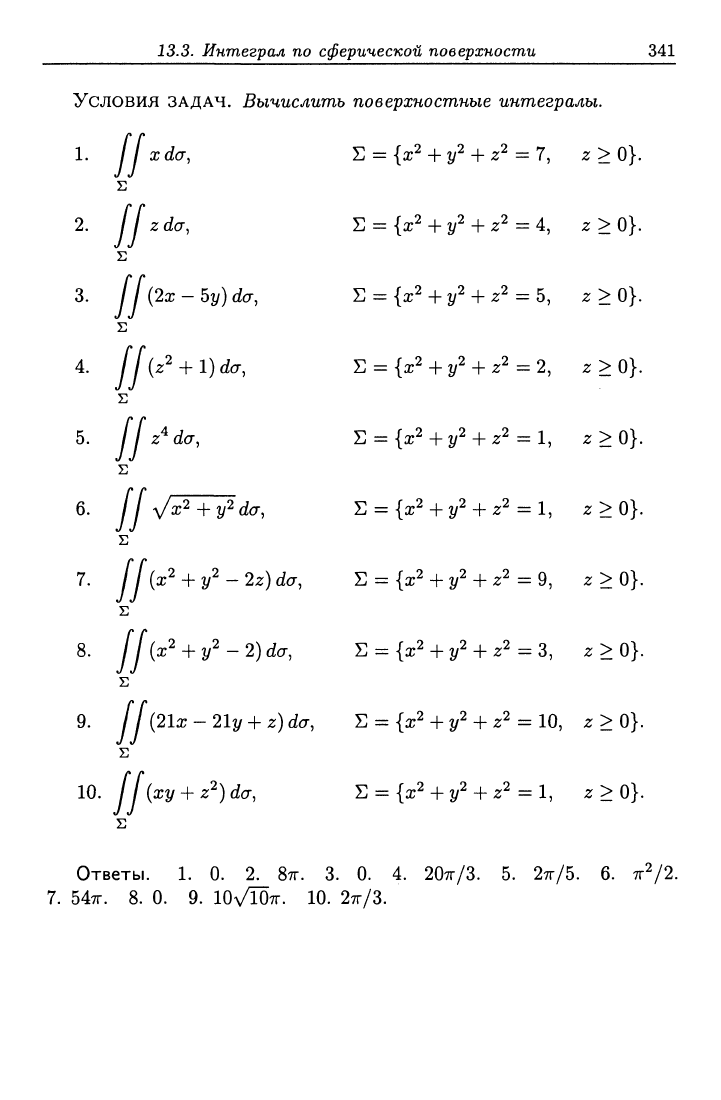
13.3.

Интеграл по

сферической

поверхности

341

Условия ЗАДАЧ. Вычислить поверхностные инт,егралы.

/ /

xdcT^

jj.da,

{2x-by)da,

5. ffz^da,

6. Ijy/^^^da,

ff{x^-\-y^-2z)da,

8. ff{x^-}-y^-2)da, Е =

9. ff{21x-21y + z)da, Е =

10.

f f {ху л-z'^) da, Е =

Е =

ж^ +

2/^

+ ^2 = 7, Z > 0}.

ж2

2/2

+ z^ = 4, Z > 0}.

ж^ -f

2/^

2:2

= 5, ^ > Q}.

x'^

+ y^ +

z'^

=2, z> 0}.

a;2-h2/2 + z2 = 1,

;г>0}.

x2 +2/^4-^2 = 1, 2>0}.

:2 + у2 + -.2 ^ 9^ ^ > Q}^

x'^

y'^

z'^

=3, z> 0}.

ж2 +

2/2

+ ^2 = 10, Z> 0}.

a;2 + 2/^-f2;2 = 1, z > 0}.

Ответы. 1. 0. 2. 87Г. 3. 0. 4. 207г/3. 5. 27г/5. 6. 7г2/2.

547Г. 8. 0. 9. ЮУДОТГ. 10. 27г/3.

Глава 14

ТЕОРИЯ ПОЛЯ

При изучении темы ТЕОРИЯ ПОЛЯ (ВЕКТОРНЫЙ АНАЛИЗ)

вы познакомитесь с понятиями векторного поля, векторных линий,

потока векторного поля через поверхность, циркуляции векторного

поля, дивергенции и ротора векторного поля. Вы научитесь вычис-

лять поток векторного поля как поверхностный интеграл, а также

использовать формулу Остроградского для вычисления потока через

замкнутую поверхность. Вы научитесь вычислять работу векторного

поля как криволинейный интеграл второго рода, а также применять

формулу Стокса для вычисления циркуляции.

С помощью пакета РЕШЕБНИК.ВМ вы можете вычислить произ-

водные, единичный нормальный вектор поверхности, дивергенцию и

ротор векторного поля, определенные и повторные интегралы, выпол-

нить все численные расчеты и проверить правильность полученных

вами результатов.

14.1.

Векторные линии

ПОСТАНОВКА ЗАДАЧИ. Найти векторные линии векторных полей

а = P{x,y)i + Q{x,y)j,

или

а = P{x^z)i-{-R{x,z)k,

или

a = Q{y,z)j-\-R{y,z)k.

ПЛАН РЕШЕНИЯ.

Запишем дифференциальные уравнения векторных линий

dx dy

Р{х,у) Q{x,y)

при

= с.

14.1.

Векторные линии 343

dx dz _,

при у = С,

Р{х,у) R{x,y,z

dy dz

при X = С.

Q{x,y) R{x,y,z)

Мы учли, что в первом случае dz = О, во втором случае dy = О и

в третьем случае dx = 0^ поскольку равна нулю соответствующая

координата векторного поля.

Решая соответствующее дифференциальное уравнение, полу-

чим, что векторные линии (в пространстве) определяются системами

уравнении

F{x,y) = Cu

f F(a:,z)-Ci,

\у = С2.

или

F{y,z)^Cu

Х = С2.

ПРИМЕР. Найти векторные линии векторного поля

а = 9zj

—

4:ук.

РЕШЕНИЕ.

Так как первая координата поля Р(х,

?/,

z) =

то

dx =

и, сле-

довательно, X ~ С. Поэтому запишем дифференциальное уравнение

векторных линий в виде:

dy dz

-— = —-— при X = С.

9z Ay ^

Решая дифференциальное уравнение, получим

Ответ. Векторные линии определяются системой уравнений

Х = С2.

344 Гл.

14.

Теория полл

Условия ЗАДАЧ. Найти векторные линии векторных полей.

а = 2уг -\-6xj. 2. а = 2xi + 3yj. 3. а = 2yi

—

Axj.

а = zi

—

хк. 5.5 = 2yj -f 3zk. 6. a = zi

—

izk.

7. a = 2zj + 9yk. S. a = Sxi + 6yj. 9. a = 3yi

—

2xj.

10.

a = yj + zk.

Ответы.

z = Ci/y,

2x2 +2/2-Ci,

Z = C2.

X = Go.

14.2.

Поток векторного поля

ПОСТАНОВКА ЗАДАЧИ. Найти поток векторного полл

а = Р(ж,

2/,

z)i-\- Q{x, у, z)j + R{x, у, z)fc

че^^ез поверхность Е, описываемую уравнением F{x,y,z)—0 и неко-

торыми неравенствами {нормаль образует острый угол с осью 0Z).

ПЛАН РЕШЕНИЯ. ПО определению поток П векторного поля а

через поверхность Е с полем единичных нормалей щ определяется

формулой

П= ff{a,no)da. (1)

Поле единичных нормалей к поверхности, заданной уравнением

F{x^y,z) = О, определяется формулой

gradF

По = ±1 7-=г7 = ±{cosa,cosp, cos7^•

gradF

14.2.

Поток векторного поля 345

Учитывал что нормали должны образовывать острый угол с осью 0Z,

т.е.

что cos 7 > О, выбираем в этой формуле знак плюс или минус.

Имеем

По

= cosm

Ч-

cosPj + cos'yk, cos 7 > 0.

Находим скалярное произведение

(5,

щ) = Р{х, у, z) cos а

-Ь

Q{x, у, z)

cos

+ R{x, у, z) cos 7 = f{x, у, z).

В силу формулы (1), поток определяется поверхностным интег-

ралом:

П= {a,no)da= f{x,y,z)da.

s s

Переходим от поверхностного интеграла первого рода к двой-

ному, проецируя Е на плоскость XOY:

П== // fix,y,z)da= // f{x,y,z{x,y))

dxdy

COS7I'

где D — проекция E на плоскость XOY; z(x, у) определяем из урав-

нения поверхности F{x^y^z)

—

ЗАМЕЧАНИЕ. Если уравнение F{x,y^z) =

не определяет одно-

значно функцию Z = z{x^y)^ то проецируем Е на другую координат-

ную плоскость или используем криволинейные координаты (можно

также разбить поверхность на части и воспользоваться аддитивнос-

тью интеграла).

Вычисляем двойной интеграл, сводя его к повторному.

Записываем ответ, не забывая о размерности.

ПРИМЕР. Найти поток векторного поля

а = —xi 4- 2yj -h zk

через часть плоскости

x + 2y + 3z = l,

расположенную в первом октанте (нормаль образует острый угол с

осью 0Z).

346 Гл.

14.

Теория поля

РЕШЕНИЕ.

Поле единичных нормалей к поверхности, заданной уравнением

F(a:,

?/,

z) = О, определяется формулой

, grad F

По

= ±1

|gradF|*

В данном случае F{x^y^z) = х

-{-

2у

-\-

—

1 и, следовательно,

{1,2,3}

По

= i-

у/и

Учитывая что нормали должны образовывать острый угол с осью

0Z,

т.е. что cos7 = ±3/\/l4 > О, выбираем в этой формуле знак

плюс. Имеем

Находим скалярное произведение:

{а,по) = —=={'-x + Ay-^3z).

Vl4

Согласно формуле (1), поток определяется поверхностным ин-

тегралом:

П = И -^{-х +

42/

-I-

3z)

d<T.

Переходим от поверхностного интеграла к двойному, проеци-

руя Е на плоскость XOY:

П = / / •у={-х -f 4у + Зг) da

где D — проекция Е на плоскость XOY и cos 7 =

Поверхность Е определяется условиями

I a;>0, 2/>0, 2:>0

dxdy

z={l~x-2y)/3 1^0^71'

14.2.

Поток векторного поля 347

Ее проекцию D на плоскость XOY находим, исключая z из условий,

определяющих Е:

/ z^{l-x-2y)/3, \

\ а;>0, j/>0, z>0 J

Г х>0, у>0, ]

Отсюда

p=L,,).0S»<l/2. 1

[^ '^^ 0<х<1-22/ J

Вычисляем двойной интеграл, сводя его к повторному:

dxdy

и= jh-x

Sz)

|cos7|

z=il-x-2y)/3

1/2 1-2у

= ^JJ{l-2x + 2y)dxdy=^ J dy J {l-2x + 2y)dx =

j^.

D 0 0

Ответ. П = 1/18 ед. потока.

Условия ЗАДАЧ. Найти поток векторного поля а через часть

плоскости^ располоэюенную в первом октанте {нормаль образует

острый угол с осью 0Z).

а = xi-hyj, X -\-у

-{•

Z = 1.

a = 2xi-\-zkj х -\-у

-\~

z = 1.

а = yj -f- zk^ 2х -i-y + z = 1.

a = xi-{-yj^ X -\-y -\-2z — 1.

—

-\-

zk, 2x + 2y + z = 1.

6. d = xi-\-yj^ 2x ~\-у-\-2z = \.

348

Гл.

14.

Теория поля

жг

2yj^ х

-\-

у + z = 1.

а = yj + zk^

2х-\-2у-\-z

= 1.

9. a = xi + 2yj + zk, x/2 + y + z/S = l.

10.

a=:xi + yj + 2zk,

ж/З

-f

2//2

Ответы.

1. 1/3

ед.

потока. 2.

1/2

ед.

потока.

3. 1/6

ед.

потока.

1/6

ед.

потока.

1/8

ед.

потока.

1/8

ед.

потока.

1/2 ед.

потока.

8. 1/8

ед.

потока. 9.

ед.

потока. 10.

ед.

потока.

14.3.

Поток векторного поля

через часть цилиндра

ПОСТАНОВКА ЗАДАЧИ. Найти поток векторного поля

= Р{х,

у,

z)i-V

Q(x, у,

z)J-f

Я(х, у, z)^

через часть поверхности

2,2

х^

-{-у

= г^,

вырезаемую плоскостями г:

и z = h

{нормаль внешняя

замкну-

той поверхности^ образуемой данными поверхностями).

ПЛАН РЕШЕНИЯ. ПО определению поток П векторного поля а через

поверхность

Е с

полем единичных нормалей

определяется форму-

лой

П= ff{a,no)da.

(1)

Поле единичных нормалей

поверхности, заданной уравнением

F{x^ у,

z) =

О, определяется формулой

gradF

= ±1

'IgradFI*

В данном случае

F{x,

у,

z) = х^ +

2/^

—

"^^

и,

следовательно,

14.3.

Поток векторного поля через часть цилиндра 349

Учитывая, что нормали должны образовывать острый угол с осью

ОХ при ж > О, т.е. cos а >

при ж > О, и тупой угол с осью ОХ при

X < О, т.е. cos а <

при х < О, выбираем в этой формуле знак плюс.

Находим скалярное произведение

(а,По) = 7=т=? ^

fi^^y.z).

V ^ +

У^

Согласно формуле (1) поток определяется поверхностным ин-

тегралом:

11= {a,no)d(7= f{x,y,z)dcT.

s s

Вводим на заданной поверхности (цилиндре) криволинейные

координаты

X =

gcosif,

y = gsm(p,

—

в этих координатах поверхность задается условиями

д = г,

О < (у9 < 27Г,

0<z<h.

Поскольку da = rd(pdz, имеем

27Г h

li = Г d(f f {г cos(f

г s'm(p,z)dz.

0 0

Вычисляем повторный интеграл и записываем ответ, не забы-

вая о размерности.

ПРИМЕР. Найти поток векторного поля

а = xi + yj + zk

через часть поверхности

вырезаемую плоскостями 2 =

и z = 2. (нормаль внешняя к замкну-

той поверхности, образуемой данными поверхностями).