Зимина О.В., Кириллов А.И., Сальникова Т.А. Высшая математика. Решебник

Подождите немного. Документ загружается.

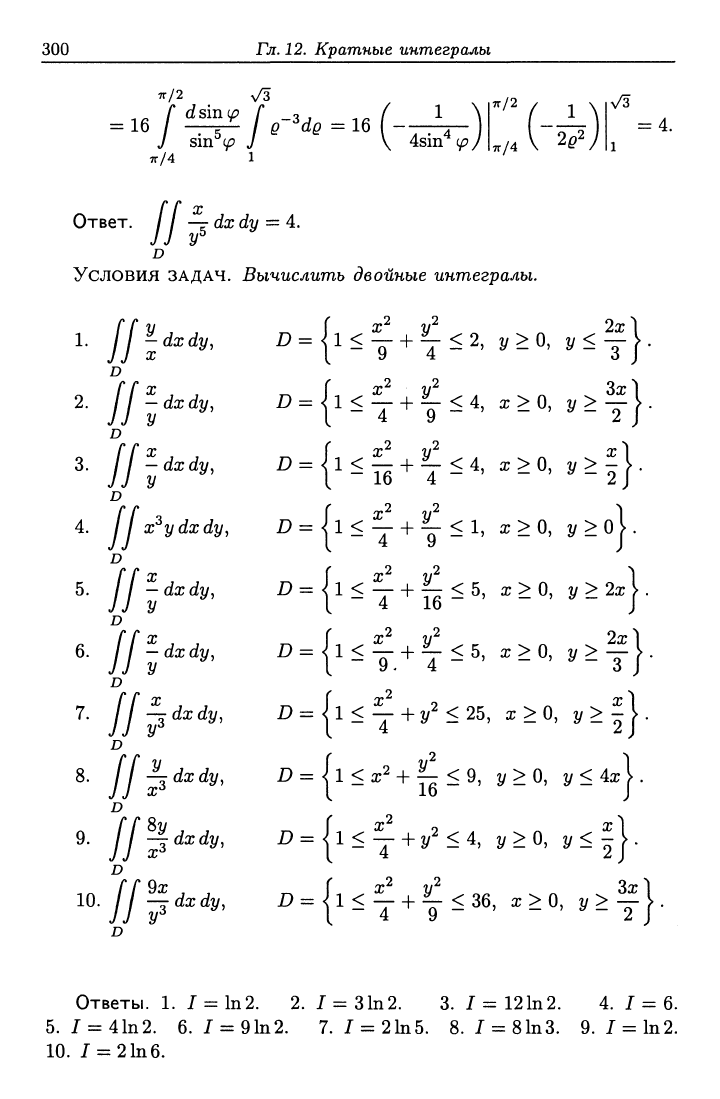
300

Гл.

12.

Кратные интегралы

Ответ

=16

Т^

f\-^d,=16

(-')

J siTTif J \ ism (pj

7Г/4 1

•//

7Г/2

7Г/4

2g'

= 4.

dxdy

Условия ЗАДАЧ. Вычислить двойные интегралы.

/ /

—

dxdy,

JJ У

'^-^

/ /

—

dxdy,

JJ У

dxdy,

D =

11 "

dxdy^

/ / ~ dxdy,

—

dxdy, D =

/ / x^ydxdy, D =

D =

dxdy^ D

411

I. Il^dxdy,

D =

?. Il^dxdy,

D =

J dx

dy^

X V

l<y + ^<2, у

2x\

>0,

y<-]

X у Зж

l<-^

+ j<i, x>0, y>-

X V X

l<^

+ ^<4, x>0, y>-).

1<^

+ у<1, х>а, y>0

1<^

+ 7т<5, x>0, y>2x

4 lb

X^ 7у2 2x

l<-9-

+ ^<5, x>0,

y>-3-^

1< —+у2<25, x>0, y>

l<x^ + Yg<9, 2/>0, y<ix).

l<^+y'<4, 2/>0, 2/<|

a;2 V^ Зж

1<^

+ Y<36, x>0, y>y

Ответы. 1. / = ln2. 2. / = 31n2. 3. / = 121n2. 4. / = 6.

J = 41n2. 6. J = 91n2. 7. / = 21n5. 8. J = 81n3. 9. J = ln2.

10.

J = 21n6.

12.5. Вычисление объемов с помощью двойного интеграла 301

12.5.

Вычисление объемов

с помощью двойного интеграла

ПОСТАНОВКА ЗАДАЧИ. Найти объем тела^ ограниченного по-

верхностями

gi{x,y)=0

(г

1,2,...),

z = fi{x,y), z = /2{х,у) {f2{x,y) > fi{x,y)).

ПЛАН РЕШЕНИЯ.

Объем цилиндрического бруса, ограниченного заданными по-

верхностями, определяется формулой

V = ЦШх.у) - fi{x,y)]dxdy, (1)

где D — проекция тела на плоскость XOY.

Чтобы найти D, задаем тело с помощью неравенств и исклю-

чаем из них Z.

Допустим, например, что координаты точек тела удовлетворяют

неравенствам

< г <

f{x,y),

gi{x^y) >

и д2{х,у) ^ 0. Тогда тело

определяется системой неравенств

gi{x,y) >0,

д2{х,у) <о,

0<z<f{x,y).

Исключая Z, получим

{

gi{x,y) >0,

{х,у):

Р2(ж,у)<0,

0<f{x,y)

Вычисляем двойной интеграл по формуле (1) при /2 = /(а:,у) и

/1=0.

Записываем ответ, не забывая о размерности.

ПРИМЕР 1. Найти объем тела, ограниченного поверхностями

ж = 17у^, x = 2v^, z =

l/2-y,

z = 0.

302 Гл.

12.

Кратные интегралы

РЕШЕНИЕ.

По формуле (1) с /2 = 1/2

—

у и Д =

искомый объем равен

{\-у)

^^^^'

где D — проекция тела на плоскость XOY.

Чтобы найти D, задаем тело с помощью неравенств и исклю-

чаем из них Z. В данном случае тело определяется системой нера-

венств

( X < 17v^,

а:>2^2^,

0<z<l/2-y

Поэтому

<х< 17V2y,

У,

у > о

г 2у/Т^<х

D=yx,y):

о<1/2-

Здесь неравенство у > О необходимо, так как у стоит под знаком

квадратного корня.

Вычисляем двойной интеграл:

V = i--y] dxdy= dy /

(-^-yjdx

D 0 2v^

1/2

= 154/2|Q-2/)v^dy = l.

Ответ. У = 1 ед. объема.

ПРИМЕР 2. Найти объем тела, ограниченного поверхностями

ж2-Ь2/^

+ 2х = 0, z = — -y'^, z = 0.

РЕШЕНИЕ.

По формуле (1) с /2 = 25/4 - у^ и /i =

искомый объем равен

ll(^-y'-0^dxdy,

12.5. Вычисление объемов с помощью двойного интеграла 303

где D — проекция тела на плоскость XOY.

Чтобы найти D, задаем тело с помощью неравенств и исклю-

чаем из них Z. В данном случае тело определяется неравенствами

Г (^+1)2+^2 <1^

\ 0<z< 25/4 - 2/2

Из первого неравенства очевидно, что \у\ < 1 и, следовательно, второе

неравенство выполняется автоматически (геометрически это озна-

чает, что проекция поверхности z — 25/4

—

у^ на плоскость XOY

охватывает круг (х-|-1)2 + 2/2<1). Поэтому

D = {{x,y): (х + 1)2 +

2/'<1}.

Так как область D ограничена окружностями и прямыми, про-

ходящими через начало координат, поставленную задачу проще ре-

шать в полярных координатах

X =

cos

(/?,

у = gsimp.

При этом (^,

ip)

е D'^

а.

искомый объем определяется формулой

V = // [-г-У^] dxdy= // ( — - ^^sin^v?! gdtpdg.

D D'

Чтобы найти область D'^ заменяем в неравенстве, определяю-

щем область D, X на gcoscp и у ка. gsimp:

{gcos(p + 1)2 4-

д^зт"^

(р

< 1.

Получаем

г,, j f ^ 0<Q<-2cosip,\

Заметим, что из неравенств

< ^ <

—2

cos

(р

следует 7г/2 <

(р

< 37г/2.

Переходим от двойного интеграла к повторному:

37г/2 -2COSV3

V = / / ( —— ^^sin^ (p\gdgd(p= / d(p / f —— g^ sin^ (p\ gdg.

7Г/2 0

304 Гл.

12.

Кратные интегралы

Последовательно интегрируя, получаем

37г/2 -2 cosy?

7г/2

37Г/2

/ /9.^л2 л4 .

M-2COSV.

7г/2

37Г/2 37Г/2

= / ( —

•

cos^ (^

—

cos"*

sin^ (р\ dip = бтг.

7г/2

Ответ. У = бтг ед. объема.

Условия ЗАДАЧ. Найти объемы тел, ограниченных заданными

поверхностями.

= у^,

= 2уД, z = l-y,

= 0.

у = у/х, у = 2i/x,

= 6 - X, Z = 0.

у = у/х, 2/ = О, х = 1,

х4-у4-1,

г = 0.

у = х^,

= 1,

= x2-hy^, z = 0.

5. t/ = б - Зх/2, 2/ = 6-Зх, г/ = 0, z = 6-x-2/, 2; = 0.

6. х2 + 2/^=4, z = xy, z = 0 (х>0, у>0).

7. у=

y/xj2,

2/ = 0

2г

= 4-х-22/, 2 = 0.

8. х2 + у^-42/ = 0, z = 4-x2, z = 0.

9. х2 + у2-2х = 0, z = x24-y^, z = 0.

10.

х^ + у2 - 2х =

О,

= 2х,

= 4х.

Ответы. 1. У = 4/15. 2. V = 48\/б/5. 3. У = 79/60. 4. V = 40/3.

У = 12. б. У = 4. 7. У = 17/5. S. V = Птг. 9. V = 37г/2.

10.

V = 27Г.

12.6.

Вычисление площадей

в декартовых координатах

ПОСТАНОВКА ЗАДАЧИ. Найти площадь области D, ограниченной

линиями /i(x, у) = О, /2(2^,2/) = О (и, возможно, прямыми X — а и

х = b или у = с иу = d).

12.6. Вычисление площадей в декартовых координатах 305

ПЛАН РЕШЕНИЯ.

Из определения двойного интеграла следует, что искомая площадь

5 численно равна

IJl-dxdy. (1)

Зададим область D неравенствами. Для этого выясним, какие

из неравенств

fi{x,y)<0, fi{x,y)>0, f2{x,y)<0 или /2(ж,2/)>0

выполняются для координат точек области D.

Пусть, например, такими неравенствами оказались fi{x,y) <

f2{x,y)<0. Тогда

Решаем неравенства, определяющие Z), относительно хиу. Получаем

а < X <Ь, I

D=l{x,

yi{x) < у < У2{х)

D=Uxy)'

^ ^ ^ ^' I

\ ' * xi{y) <х< Х2{у) J *

Переходим от двойного интеграла к повторному:

b 2/2 (ж)

dxdy = dx / dy

D a 2/1 (x)

или ^ . .

dxdy = dy / dx.

D с xi{y)

Последовательно интегрируем, используя свойства определен-

ного интеграла.

Записываем ответ, не забывая о размерности.

ЗАМЕЧАНИЕ. ЕСЛИ необходимо, разбиваем область на части и ис-

пользуем свойство аддитивности интеграла.

306 Гл.

12.

Кратные интегралы

ПРИМЕР. Найти площадь области D, ограниченной линиями

х^

+ у^ = 12, ж\/б = 2/2 (а:>0).

РЕШЕНИЕ.

Зададим область D неравенствами. Область не может нахо-

диться вне круга, так как тогда она неограничена. Область не может

находиться слева от параболы, так как в этом случае ее точки могут

иметь отрицательные абсциссы, что исключено условием х > 0. Сле-

довательно,

Решаем неравенства, определяющие

Z>,

относительно хпу. Получаем

0.2

^ <

< ч/12 - у2.

Следовательно,

y'^/V^

< y/l2

—

y^. Отсюда ~\/б <у< \/б. Итак,

-у/Е < 2/ < \/б, 1

D=< (х,2/):

2/VV6 <х< х/12 - у2

Вычисляем площадь области D по формуле (1). Переходя от

двойного интеграла к повторному, получим

^ А/12-2/2

S = dxdy = dy / da:.

^ -V6 yVVe

Используя свойства определенного интеграла, последовательно

интегрируем:

S= f dy f dx= f (^х/Тг"^--^") dy = 37r + 2.

Ответ. 5 = (Зтг -h 2) (ед. длины)^.

12.7. Вычисление площадей в полярных координатах 307

Условия ЗАДАЧ. Найти площади фигур, ограниченных задан-

ными линиями.

2/ = 2/а;, у = ^е", у = 2, у = А.

у = 1/х, 2/ = 2е^, у = 1, у = 2.

у = 2/ж, у = 2^/x,

= 4.

х2 4-2/2 = 2, у = -х'^ (2/<0).

2/ = >/ж, 2/ =

О,

= 4.

= 2

—

2/^,

= —у.

2/ = sinx, y = cosx, ж = О, ж = 7г/4.

8. 2/ = 2а:^ - 1, у = ж.

9. х = А/4 - 2/2,

= 2/V3.

10.

2/ = In

а:,

у = е/х, х = 1.

Ответы. 1. 5 = 2. 2. 5 = 1. 3. 5 = 28/3 - In

16.

4. 5 =

= 7г/2 + 1/3. 5. 5 = 16/3. 6. 5 = 7/6. 7. 5 = v^ - 1. 8. 5 = 27/24.

9. 5 = 27Г/3 - \/3/б. 10. 5 = е - 1.

12.7.

Вычисление площадей

в полярных координатах

ПОСТАНОВКА ЗАДАЧИ. Найти площадь области D, ограниченной

двумя окруэюностями

2/2 + ai2/ + hx + а:^ =

О,

2/^ + «22/ +

^2^:^

ж^

= О,

(fli =0, 02 = О, 6162 >

или bi =0, 62 = О, aia2 > 0)

и двумя прямыми

тп\у

Н-

kix = О, (mf + kl ^ 0), Ш22/ +

/i^2a:

= О, (т| +

А:^

т^ 0).

308 Гл. 12. Кратные интегралы

ПЛАН РЕШЕНИЯ. ИЗ определения двойного интеграла следует, что

искомая площадь S численно равна

5= И I- dxdy. (1)

Так как область D ограничена окружностями и прямыми, про-

ходящими через начало координат, поставленную задачу проще ре-

шать, переходя к полярным координатам

X — р cos

V?,

у = р sin

и записывая уравнения границ в полярных координатах.

При этом область D перейдет в область D', а искомая площадь

будет равна

5 = / /

dip.

Зададим неравенствами область D' в полярных координатах:

\ ' * Pl{^) <Р<Р2Ы J *

Переходим от двойного интеграла к повторному:

S = dip / pdp

и вычисляем его, пользуясь свойствами определенного интеграла.

Записываем ответ, не забывая о размерности.

ПРИМЕР. Найти площадь фигуры, ограниченной данными лини-

ями

2/2-42/ + а:2=0, y^-Sy + x^ =0, ^ ^ ^' ^ " ^'

РЕШЕНИЕ.

Так как область D ограничена окружностями и прямыми, про-

ходящими через начало координат, поставленную задачу проще ре-

шать, переходя к полярным координатам

X = pcosip,

у = psimp.

12.7. Вычисление площадей в полярных координатах 309

При этом область D перейдет в область

JD',

ограниченную линиями

7Г

g =

4:Siinp,

= Ssmip, ^ =

, ^ =

"2 *

А искомая площадь будет равна

5 = / / gctgdip.

Зададим неравенствами область D' в полярных координатах:

sin

< ^ <

Переходим

от

двойного интеграла

повторному:

7г/2 8sin(^

S = dip / gdg.

7г/6 4 81П<^

Последовательно интегрируя, получим

7г/2 8sin(^ 7г/2 Q . 7г/2

S = d(p / ^d^= /9

dip

24:

sin^ (^dv? =

47Г

+ ЗУЗ.

J J

14 sin (^

«^

7г/6 4sinv? 7г/6 7г/6

Ответ. 5 = (47Г + 3\/3) (ед. длины)^.

Условия ЗАДАЧ. Найти площади фигур^ ограниченных задан-

ными линиями.

1. у'^-3у

+ х^=0, 2/2-52/ +ж^ = О, y = x/V3, х = 0.

2/^ +

32/

а^^

О,

2/^ + % +

а^^

О, 2/

= а:,

= 0.

3. у'^

-Зу +

х'^

=0, 2/^ -

72/

+ ^2 =

О, 2/

= VS^, х = 0.

2/^ + 32/ + ^2 = О, 2/^ +

^2/

+ ^2 = О, у = х, у = х/л/З.

2/^ - 32/ + ic^ = О, 2/^ -

^2/ Н-

а^^ = О, у =

х/\/3,

х = \/Зх.