Зимина О.В., Кириллов А.И., Сальникова Т.А. Высшая математика. Решебник

Подождите немного. Документ загружается.

или

290 Гл.

12.

Кратные интегралы

Пусть, например, такими неравенствами оказались fi{x,y) <

f2{x,y)<0. Тогда

Решаем неравенства, определяющие D, относительно хиу. Получаем

D=\^{x,y):

y^^^)llly^^^)

Переходим от двойного интеграла к повторному:

6 У2(х)

// f{x,y)dxdy= dx f{x,y)dy

D a yi{x)

или

d X2{y)

// f{x,y)dxdy= dy f[x,y)dx.

D с XIЫ

Последовательно интегрируем, используя свойства определен-

ного интеграла.

Записываем ответ.

ЗАМЕЧАНИЕ. Если необходимо, разбиваем облгьсть на части и ис-

пользуем свойство аддитивности интеграла.

ПРИМЕР.

Вычислить двойной интеграл

//<

где область D ограничена линиями х = \^у=^х^иу= —^/x.

РЕШЕНИЕ.

Зададим область D неравенствами. Очевидно, что —^ < х^.

Поэтому —у/х < у < х^. Поскольку X фигурирует под знаком квад-

ратного корня, X > 0. Для X возможны неравенства

< х < 1 или

1 < X. Во втором случае область неограничена, что неприемлемо.

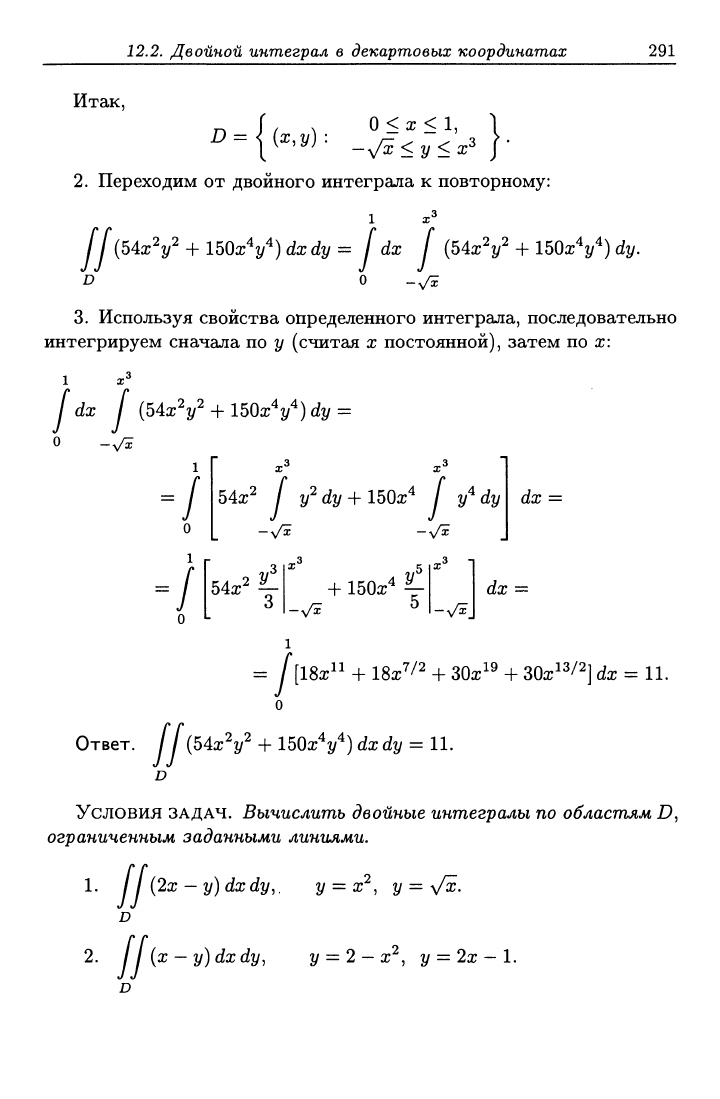
12.2.

Двойной интеграл в декартовых координатах

291

Итак,

D=< (х,2/):

-у/х

Переходим от двойного интеграла к повторному:

1 х^

[[{БАх'^у^ + ISOx'^t/^) dxdy= f dx f (54x^2/2 + ISOx^y'*) dy.

0 -v^

Используя свойства определенного интеграла, последовательно

интегрируем сначала по у (считая х постоянной), затем по х:

f dx [ {БАх^у^ + 150x^2/^) dy =

о -v^

^3 х^

/* 54^2 / y^dy + 150ж^ /

2/^

—

у/х

—у/х

dx =

-I

ЬАх

\—\/х \—y/xj

Ответ.

= f[18x^^ + 18x^/2 + 30a;^^ + ЗОж^^/^] dx = 11.

[[{Ых'^у^ 4- 150x^2/^) dxdt/ = 11.

Условия ЗАДАЧ. Вычислить двойные интегралы по областям J9,

ограниченным заданными линиями.

I j {х

—

y)dxdy^ у = 2 -

х'^у

у = 2х-1.

292 Гл.

12.

Кратные интегралы

{ylnx)dxdy, у=-, У = Vx, х = 2.

{cos2x + sin у) dxdy, t/=--— ж, у =

х = 0.

sm{x-\-у) dxdy, у = х, 2/ = -^, ж = 0.

6. —dxdy, у = -',у = х,х = 2.

{х'^

-{-y)dxdy, у = х^,

= у/х.

8. {2х

—

y)dxdy, у = х^,

= х, х = 1, х = 2.

10.

x^y^^/l^-x^^-y^dxdy,

?/=\/l

—х^, 2/= О, х = 0.

Ответы. 1. / = 1/10. 2. J = 64/15. 3. / = 5(21п2 - 1)/8.

/ = (тг + 1 - 2л/2)/4. 5. / = 1. 6. / = 9/4. 7. 7 = 33/140.

8. / = 9/10. 9.7 = 7г/б. 10. 7 = 4/135.

12•З.

Двойной интеграл

в полярных координатах

ПОСТАНОВКА ЗАДАЧИ. Вычислить двойной интеграл

// f{x,y)dxdy,

где область D ограничена двумя окруэюностлми

У^

4- сцу 4- bix + х^ =

О,

2/^ +

а2У

-f

62Х

-f х^ =

12.3.

Двойной интеграл в полярных координатах 293

(ai =0, а2 = О, 6162 > О или 6i =0, 62 = О? <^ict2 > 0)

и двумя прямыми

тпгу

4- kix = О, (ш^

-\-

kl ф 0), т22/ +

А^г^:

= О, {ml -\-к\ф 0).

ПЛАН РЕШЕНИЯ.

Зададим область D неравенствами в декартовой системе коор-

динат.

Для этого заметим, что окружности

у"^

+ аху

-\-

bix

-\-

х^ = О и

у^ -f 022/ +

^23:

ж^

= 0 проходят через начало координат и их центры

расположены на оси ОХ (при ai = О, а2 = 0) или на оси 0Y (при

bi = О, 62 = 0) по одну сторону от начала координат (так как 61^2 >

или aia2 > 0). Поэтому та из окружностей, которая имеет меньший

радиус, расположена внутри другой. Пусть, например, это окруж-

ность

2/^

Н-

^12/

+ bix + х^ =0. Область D находится между окружнос-

тями, поэтому координаты точек области D удовлетворяют неравен-

ствам

У^

-h aiy + bix +

ж^

> О, 2/^ +

а2У

Ь2Х

ж^

< 0.

Прямые miy + kix = О и т2у + к2Х = О проходят через начало

координат. Область D расположена между ними. Учитывая, в ка-

кой полуплоскости находятся окружности и, следовательно, область

определяем, каким из следующих пар неравенств удовлетворяют

координаты точек области D:

чт^гУ

+ kix > О, 77122/ + ^2Х > О,

ТП1У

+ kix < О, 77122/ + ^2Х > о,

^12/

"Ь

^1^^

О?

^22/ + ^2^ < О,

^12/

^1^

О?

^^22/ +

^2^^

^ 0.

Так как область D ограничена окружностями и прямыми, про-

ходящими через начало координат, поставленную задачу проще ре-

шать в полярных координатах

( X =

Q cos (/?,

\ у =

gsiiKf.

При этом (^, if) е D\ г. искомый интеграл определяется формулой

// f{x,y)dxdy= / / f

{д

cos

(р,д

sin (f)gdg

dip.

294 Гл.

12.

Кратные интегралы

Чтобы найти область £)', заменяем в неравенствах, опреде-

ляющих область D, X на gcosf и t/ на gsiinp. Затем разрешаем

полученные неравенства относительно ди

^р.

Таким обргизом получим

Переходим от двойного интеграла к повторному:

S = d(p / f

{д cos

у д

sin (f) gdg

И последовательно интегрируем, используя свойства определенного

интеграла.

Записываем ответ.

ПРИМЕР. ВЫЧИСЛИТЬ двойной интеграл

dy^

II-

где область D ограничена линиями

2/^

- 4г/ + а;2 = О, у^ - Зт/ + х^ =

О,

у = x/Vs, х = 0.

РЕШЕНИЕ.

Зададим область D неравенствами в декартовой системе коор-

динат. Для этого заметим, что, выделяя полные квадраты в урав-

нениях окружностей 2/^

—

4^/ + ж^ = О и у^

—

-\-

х^ = О, их можно

привести к виду

(у-2)2+ 0:2 = 4, (1)

{у - 4)2 +х^ = 16. (2)

Очевидно, что обе окружности проходят через начало координат

и их центры расположены на оси 0Y в точках (0,2) и (0,4). Ок-

ружность (1) имеет радиус 2 и, следовательно, лежит внутри окруж-

ности (2), имеющей радиус 4. Поскольку область D находится между

окружностями, координаты ее точек удовлетворяют неравенствам

{у ~ 2)2 + ^2 > 4, (у - 4)2 + х2 < 16.

12.3.

Двойной интеграл в полярных координатах

295

Прямые у = х/у/З и а: =

проходят через начало координат. Об-

ласть D расположена между ними. Учитывая, что окружности, а

следовательно, и область D находятся в верхней полуплоскости, за-

ключаем, что область D находится над прямой у = х/у/З и справа от

прямой X = 0. Поэтому координаты точек области D удовлетворяют

неравенствам

у >

ж/\/3,

ж > 0.

Итак,

D= <

(2/-2)2+х2>4,

(х,2/):

(2/- 4)2+0:2 < 16,

у >

х/\/3,

X >

Так как область D ограничена окружностями и прямыми, про-

ходящими через начало координат, поставленную задачу проще ре-

шать в полярных координатах

I У

д cos

v?,

у = Qsinip.

При этом (^, (^) G

JD',

а искомый интеграл определяется формулой

xdxdy= gcosip

gdQd(f.

D D'

Чтобы найти область D', заменяем в неравенствах, определяю-

пщх область D, х на дcos if и t/ на gsiiup:

[ {gshiip - 2)^ + д^ cos^

</?

> 4,

{д

sin

- 4)2 +

д^

cos^ if < 16,

^ gcosip ^ ^

gsm(p>—j=r—^ gcos(p>0.

Решая эти неравенства относительно ^ и (^, получаем

7г/6 < (^ < 7г/2,

D'={

(^,^):

sin

< ^ <

sin

(/?

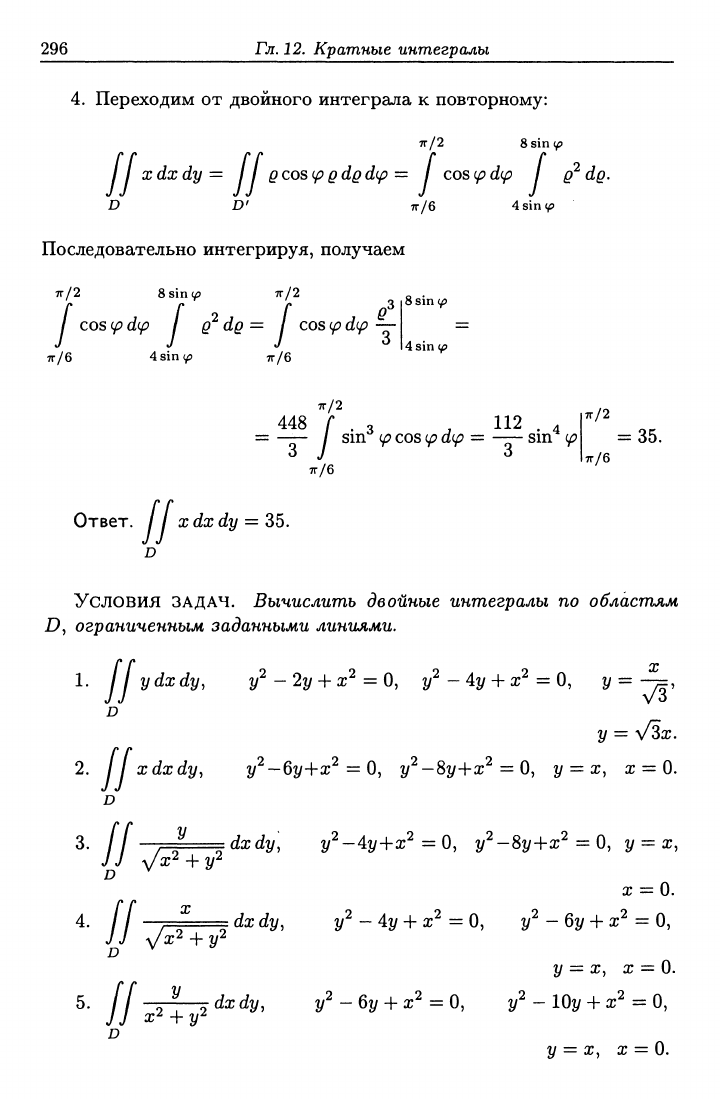
296

Гл.

12.

Кратные интегралы

Переходим от двойного интеграла к повторному:

7г/2 8sinv?

xdxdy= //

д cos

dip

= / cos

ip dip

/ g^ dg.

D D' 7г/6 4s\inp

Последовательно интегрируя, получаем

7г/2 8sin<^ 7г/2

COS (pdcp

/ g^ dg = с

7г/6

4sinv? 7г/6

Ssinv?

4 sin

7Г/2

448 /• . 3 , 112 . 4

-— / sm

(/?

cos

ipdip

= -— sm (^

о J о

т/6

7г/2

7г/6

35.

Ответ. xdxdy = S5.

Условия ЗАДАЧ. Вычислить двойные интегралы по областям

ограниченным заданными линиями.

' !!'•

Ilydxdy, у^-2г/ + ж^=0, 2/ - 4?/+ ж^ = О, 2/=-7^,

= \/Зж.

xdxdy,

2/^

—б2/+а:^=0, у^-^у+ж^ = О, 2/= ж, х = 0.

П —^=S==dxdy, 2/ -42/+2:'= О, 2/ -Sy+a;" = О, 2/= а:,

У^^Ту"

4. [[

—=L==dxdy,

2/^-42/^-ж^=0, 2/^ - 62/+ ж^ = О,

лУх^-\-у^

= ж,

= 0.

/ / ^ " ^ dxrfy, 2/^ - 6у

Н-

х^ = О, у2 - 102/ + х^ = О,

= X, X = 0.

//.

12.4. Интеграл в

обобщенных

полярных координатах

297

// ^^

^dxdy, у^-2х +

х'^

= 0, у2-4х +

ж2

= 0,

J J х^Л-у^

ij-^—^dxdy,

2/2-4х + х2=0, у2-6х + х2=0,

= --^, г/ = \/Зх.

-r—^dxdy,

2/^-4а: +

ж2

= 0, г/2

82:

+ х^ = О,

У У

х^ +

у = О, 2/ = \/Згг.

^ Л«.

xJ«.

«.2

о^

п «.2

л«.

«.2

л/ж2 4- 2/2

9. jl—^=====dxdy, 2/^-2x-f

ж^

= 0, 2/^-бх + х^ = 0,

10.

/ /

da;

с?2/,

2/^

2а:

+ х^ =

О,

2/^

Юж

+ х^ = О,

х/жМм/"

= \/Зх,

= О-

Ответы.

1. / =

—(27Г

\/3).

2. / =

IS^.

3. 7 =

10\/2.

/=^(4-х/2).

/=l +

f. 6.

/=J.

/=А(27г-г/3).

8. 7=..^-^.

7=2Н. 10.

7=1^^.

90 15

12.4,

Двойной интеграл в обобщенных

полярных координатах

ПОСТАНОВКА ЗАДАЧИ. Вычислить двойной интеграл

1 1 f{x,y)dxdy,

где область D задана неравенствами

с\<^-\-\^<с1 (а > О,

> О, ci > О, С2 > 0),

а^

298

Гл.

12.

Кратные интегралы

miy-}-kix>0 (ml +

kl^O),

шгу +/сгх >

{ml +

kl^O).

ПЛАН РЕШЕНИЯ.

Область D задана неравенствами в декартовой системе коорди-

нат, т.е.

D= <

^1 - ^9. ^ L9 - ^2?

{х^у)-

miy + kix>0,

1^2У

+ к2Х >

Так как область D ограничена эллипсами и прямыми, проходя-

щими через начало координат, поставленную задачу проще решать в

обобщенных полярных координатах

= ад

cos

ip,

у =

sin

(р.

При этом {д,(р) G -D', а искомый интеграл определяется формулой

// f{x,y)dxdy= // f

{ад cos (p,bg

sin (p)abgdg

dip.

D D'

Чтобы найти область D', заменяем в неравенствах, определяю-

щих область Z), х на ад

cos (р

и у из. bgsimp. Затем разрешаем полу-

ченные неравенства относительно д и ip. Таким образом, получаем

Переходим от двойного интеграла к повторному:

// f{x^y)dxdy = ab d(p f{адcos(р,bgsimp)gdg'^

и последовательно интегрируем, используя свойства определенного

интеграла.

Записываем ответ.

ПРИМЕР.

Вычислить двойной интеграл

— dx dy,

уЬ

12.4. Интеграл в

обобщенных

полярных координатах

299

где область D задана неравенствами

1<^+2/^<3,

2/>~, ^>0.

РЕШЕНИЕ.

Область D задана неравенствами в декартовой системе коорди-

нат:

Так как область D ограничена эллипсами и прямыми, проходя-

щими через начало координат, поставленную задачу проще решать в

обобщенных полярных координатах

{

X = 4^cos(^,

у = gsiiiip.

При этом

{д,

if) £ D',

искомый интеграл определяется формулой

Чтобы найти область D\ заменяем в неравенствах, определяю-

щих область D, X на ад cos

и у на

Ьд

sin

ip:

16^^

cos^

-f-

sin^

< 3,

^ igcosif

gsm(p > ,

cos

> 0

Решая эти неравенства относительно д и ip, получаем

1 <

< \/3, ]

{{g,^):

7г/4 < (^ < 7г/2

Переходя от двойного интеграла к повторному и последова-

тельно интегрируя, получаем

llfsd^dy=ll

4gcos(p

^^.^5 ^^ ^^ "^

7г/2 Уз

^^ sm (f

7г/4

^ j d^jm-'.'^de

sm (^