Зимина О.В., Кириллов А.И., Сальникова Т.А. Высшая математика. Решебник

Подождите немного. Документ загружается.

260 Гл.

11.

Дифференциальные

уравнения

получаем дифференциальное уравнение относительно С{х)

С\х)х = -^,

х^

Это уравнение с разделяющимися переменными.

Разделяя переменные

dC = —г ^'^

х-^

и интегрируя, получаем

С(х) = ^ + Со,

где Со — произвольная постоянная.

Таким образом, общее решение неоднородного уравнения (8)

имеет вид

Используя начальное условие у{1) = 1, получаем

находим Со =

и подставляем в общее решение (9).

Ответ, у = 1/х.

2-й способ.

Ищем решение уравнения (8) в виде

у = u{x)v{x),

где и и V — неизвестные функции х.

Уравнение (8) принимает вид

1 2

u'v + uv'

= Г-. (10)

X Х^

Поскольку теперь мы имеем две неизвестные функции, а урав-

нение, которому они должны удовлетворять, только одно, то еще одно

уравнение мы можем принять произвольно, лишь бы оно не сужало

множество решений у.

11.4. Линейные уравнения l-zo порядка 261

Пусть одна из функций (например, и{х)) удовлетворяет уравне-

нию

и' -^и = 0. (11)

Тогда уравнение (10) принимает вид

v'u^-\.

(12)

х^

Решая уравнение (11) (с разделяющимися переменными), находим

и{х)

—

Ах,

где А — произвольная постоянная {А ф О, чтобы не сужать множест-

во решений).

Подставляем и{х) в уравнение (12) и решаем его относитель-

но v\

,_ Jl_ _ JL_

Ах^ Ах'^ '

где В — произвольная постоянная.

Записываем обш;ее решение уравнения (8) в виде

у{х)

—

u{x)v{x) = —h Сж,

где С = АВ — произвольная постоянная.

6. Используя начальное условие у{1) = 1, находим С = 0.

Ответ, у = 1/х.

Условия ЗАДАЧ. Найти решения задач Коти для дифференци-

альных уравнений.

Х2/' + у-е^=0, 2/(0) = 1.

y'-ytgx= , 2/(0)=0.

cos ж

о2

у' cos^x^-y = igx, у(0)=0.

262 Гл. 11. Дифференциальные уравнения

у' -ytYix —

Q}O?

X, у(0)=0.

10.

1 У 1

у — = х\пх,

хтх

у'

smx

—

2/C0SX = 1,

у'

—

ytgx = cos ж,

у'

- 2ху = 3x2 _ 2^.4^

ху'

—

2у = 2ж'*,

у'

+ у cos

а;

= е^^'^^,

Ответы.

е^-1

—

e~*Sa:

_|_

tgX - 1.

— -—-

^ 2

(X sin 2х \ 1

'^^ V2 "^ 4 j cosx'

у~х^-

х^.

2/(е) = у.

уф

о.

У(0)=0.

у(0)=0.

у(1)=0.

у(0)-0.

у =

8. у =

10.

у =

а;

cos а;'

sh х.

cos

х^

а;е-^'"^.

11.5.

Уравнение Бернулли

ПОСТАНОВКА ЗАДАЧИ. Найти решение задачи Коши для уравне-

ния Бернулли

+ 9{x)y = f{x)y^ (а ^0,1) (1)

С начальным условием

У{х^) =

2/0.

(1')

ПЛАН РЕШЕНИЯ.

С помощью подстановки

ургшнение приводится к линейному

z'+p{x)z = q{x), (2)

11.5. Уравнение Бернулли 263

где

р = {1 - а)д и q = {1 - a)f.

Решаем линейное уравнение (2) и делаем замену z = у^~^.

Используя начальное условие (1'), находим решение поставлен-

ной задачи Коши.

Записываем ответ в виде у =

(f{x).

ЗАМЕЧАНИЕ. При решения уравнения Бернулли можно не при-

водить его к линейному, а искать решение в виде у = u{x)v{x) или

применять метод вариации произвольной постоянной.

ПРИМЕР. Найти решение задачи Коши

ху' -\-у = ху'^ (3)

с начальным условием

2/(1) = 1.

РЕШЕНИЕ.

Преобразовав уравнение к виду

1 2

У +-у = у,

убеждаемся, что это уравнение Бернулли с а = 2.

С помощью подстановки

уравнение

(3)

приводится

линейному

z'--z

= -l. (4)

Решаем уравнение (4) методом вариации произвольной посто-

янной:

а) решаем однородное уравнение

--z = 0,

получаем z = Сх\

б) ищем решение неоднородного уравнения в виде

С{х)х\

264

Гл.11.

Дифференциальные

уравнения

в) подставляя в уравнение (4)

Z = С{х)х, z' = С\х)х 4- С{х),

получаем уравнение с разделяющимися переменными

С'{х)х

= -1.

Разделяя переменные и интегрируя, получаем

С{х) = Со-1пх.

Таким образом, общее решение неоднородного уравнения (4) имеет

вид

Z = х{Со -

ж),

или, после замены z = у~^,

X{CQ - In

Ж)*

Используя начальное условие у(1) = 1:

1(Со-0)

получаем Со = 1.

Ответ, у =

х{1

—

In ж)

Условия ЗАДАЧ. Найти решения задач Коши для дифференци-

альных уравнений.

ху' = 4у =

х'^уГу,

у{1) = 0.

, 2ХУ 4:у/у (Л\ '^^

^- ^1Т^

7гт^'"*'"' '^'^^^

ху' + у = -х^у^, У(1) = 1-

11.6. Уравненгт в полных дифференциалах 265

ху' + у =

у^1пх,

у{1) = 1.

(х + 1)у' + у = -у^{х + 1), 2/(0) = 1.

6. 2/' + 2y = eV,

2/(0)-1.

у' +

= х2/2, 2/(0) = 1.

X cos^a: тг^

9. yshx-i-ychx = -Y-y, ^^^ "^ ihl'

10.

у'- 2/tgx+ у^со8ж = О, 2/(0) = 1.

Ответы.

2/ = "Г lii^ к1- 2. 2/ = (1 + x^)arctg^

ж.

3. 2/ = -^.

4 х^

'•У = Т^х- ^•y=il + x){llln\l + x\y

^-У^'-'-

1 „ /l+ln|cosx| V „ 1

10.

- ^

{х + l)cosx*

11.6.

Уравнения в полных дифференциалах

ПОСТАНОВКА ЗАДАЧИ. Найти интегральные кривые дифферен-

циального уравнения

P{x,y)dx + Q{x,y)dy = 0. (1)

ПЛАН РЕШЕНИЯ.

Если в некоторой области D Р(ж, у) и (5(х, у) имеют непрерыв-

ные частные производные и выполнено условие

ду

~~ дх'

то P{x^y)dx + Q{x,y)dy — дифференциал некоторой функции

и{х,у).

Тогда уравнение (1) называется уравнением в полных диффе-

266 Гл.И.

Дифференциальные

уравненил

репциалах и может быть записано в виде

dU{x,y) = 0, {!')

где и{х^ у) — дважды непрерывно дифференцируемая неизвестная

функция.

Из (1') следует, что интегральные кривые определяются уравне-

нием и{х,у) = С при всевозможных значениях С.

Для отыскания U заметим, что

^=Р{х,у),

^ = Qix,y). (2)

Интегрируя первое равенство в (2) по ж, получим

и= I P{x,y)dx^ip{y),

где (р{у) — неизвестная функция, которую еще предстоит найти.

Дифференцируя U по у, имеем

-JP{x^y)dx-,^iy),

Используя второе равенство в (2), получим уравнение

— P{x,y)dx-\-(p'{y) = Q{x,y).

Находим (р{у) и затем U{x,y).

Ответ. Интегральные кривые определяются уравнением

U{x^y)

= C

при всевозможных значениях С

ПРИМЕР. Найти интегральные кривые дифференциального урав-

нения

xdy

—

ydx ^ ,^.

xdx-^ydy+ \ ^\ :^0. 3

х^

Л-у^

РЕШЕНИЕ.

Преобразуем уравнение (3):

^ ^ dx^iy^ -Т^ ) ^У = О-

х^

-\-у^ J \ х^ -\-у

11.6. Уравнения в полных

дифференциалах

267

В данном случае

Р{х,у)= (х-—L), Q{x,y)=\y +

х^

-\-

у J \ х^

-\-1

Эти функции непрерывно дифференцируемы в области х^ + у^ > 0.

Кроме того,

Поэтому P{x.,y)dx-\- Q(x,у) dy — дифференциал некоторой функции

17(а;, у) в любой односвязной области J9, не содержащей точку а; = О,

= 0. Следовательно, уравнение (3) является уравнением в полных

дифференциалах и может быть записано в виде

dU{x^ у) = 0 при

(ж,

у) е D.

При этом

ди _ у ди _ X . .

'д^~''~

х^ + у^'

'д^~^^

х^ + у^' ^^

Интегрируя первое равенство в (4) по ж, получим, что при у ^

где ^{у) — неизвестная функция, которую еще предстоит найти.

Дифференцируя U по у, имеем

ди X

^'{У)'

ду ^2 4-

2/^

Используя второе равенство в (2), получим

+ ^\у) = у +

После преобразований имеем

^'{у) =

У'

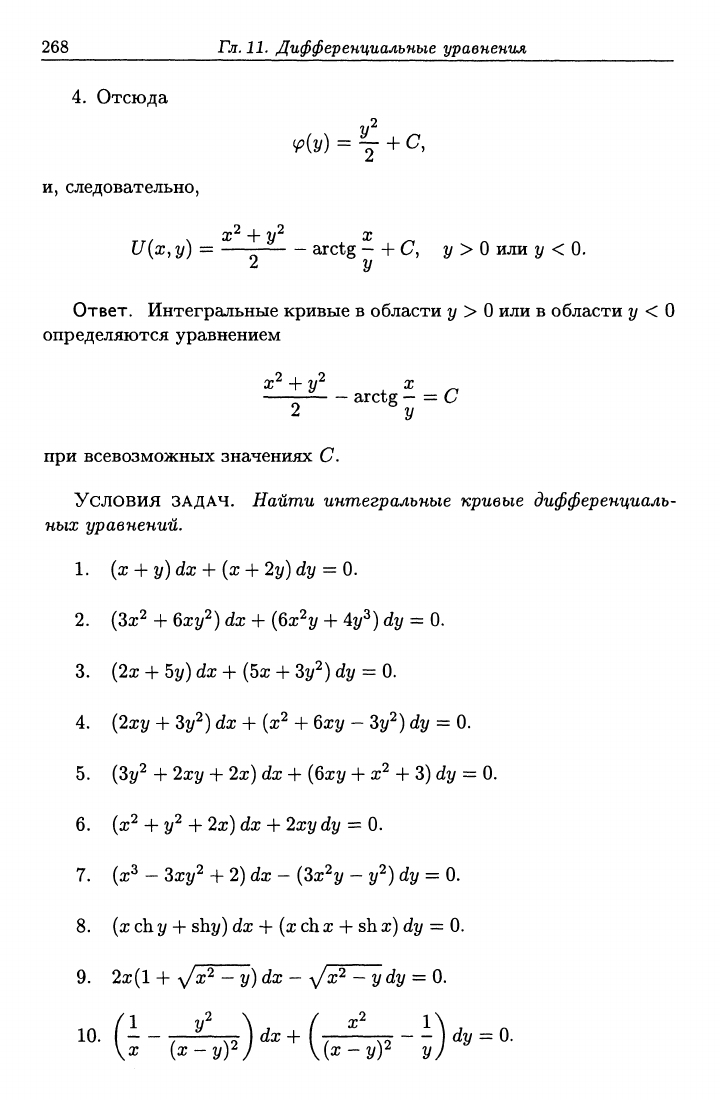
268 Гл.

11.

Дифференциальные

уравненил

Отсюда

и, следовательно,

v'(y) = Y + c,

"4"

у X

и{х, у) = —~ arctg - + С, у >

или у <0.

^ У

Ответ. Интегральные кривые в области у >

или в области у <

определяются уравнением

2 У

при всевозможных значениях С.

Условия ЗАДАЧ. Найти интегральные кривые дифференциаль-

ных уравнений.

(ж

2/)

da;

+ (ж + 2у) dy = 0.

(Зж^

Ч-

6ж?/2) dx -f (бж^г/ 4- V) dy = 0.

(2ж + Бу) dx -h (5ж -f Зу2) di/ = 0.

(2жу 4- Зу^) dx + (ж^ + бжу - Зу^) dy = 0.

(Зу2 +

2ж2/

+ 2ж) dx -f (бжг/ +

ж2

+ 3) dy = 0.

6. (ж^ + у^ + 2ж)

с^ж

+ 2ху dy = 0.

(ж^ - Зж2/2 4- 2) с/ж - (Зж^у - У^) dy = 0.

8. (жсЬу 4-shy)dж 4-(жсЬж 4-shж)dг/= 0.

9. 2ж(1 4- i/^2 - у) dx - >/ж2 ~ydy = 0.

\х (ж-у)2у V(^-2/)^ У/

11,7. Уравнения вида F(a:,2/(^\y(^+^^) =

269

Ответы.

—+ху +

у'^

= С. 2. х^ + Зх^у'^

Jry"^

= С.

х^

Л-

Ъху + у^ = С. 4. х^у

Зху^ -у^ =С.

х^

Зжт/^ + х'^у + Зу + ^2 = а 6. — + ху'^ Л-х^ = С.

7. — - •-ж^у^ + 2х + ^ = С. 8. yshx +

a;shy

= a

9. х2 + |(:с2 4- уУ/' = а 10. -^^ + In - = С.

3 х-у у

11.7-

Уравнения вида F{x,y^^\y^^'^^^) =

ПОСТАНОВКА ЗАДАЧИ. Найти общее решение дифференциального

уравнения

F{x,y^'\y^'-^'^) = 0

ПЛАН РЕШЕНИЯ.

Полагая у^^^ = ^(а^)? получим дифференциальное уравнение

первого порядка

F{x,p,p')=0.

Определяя тип этого уравнения и применяя соответствующий

метод решения, находим р = f{x,Ci), где Ci — произвольная посто-

янная.

Так как р

—

у^^\х)у

имеем

yW = /(x,Ci).

Последовательно интегрируя к раз (при каждом интегрировании не

забывая о произвольной постоянной), получим ответ

у = 9?(ж,С1,С2,...,Сп), п = к + 1,

Ci,

Сг,..., Сп — произвольные постоянные.

ПРИМЕР. Найти общее решение дифференциального уравнения

{1-\-х^)у'' + 2ху' = 12х\