Зимина О.В., Кириллов А.И., Сальникова Т.А. Высшая математика. Решебник

Подождите немного. Документ загружается.

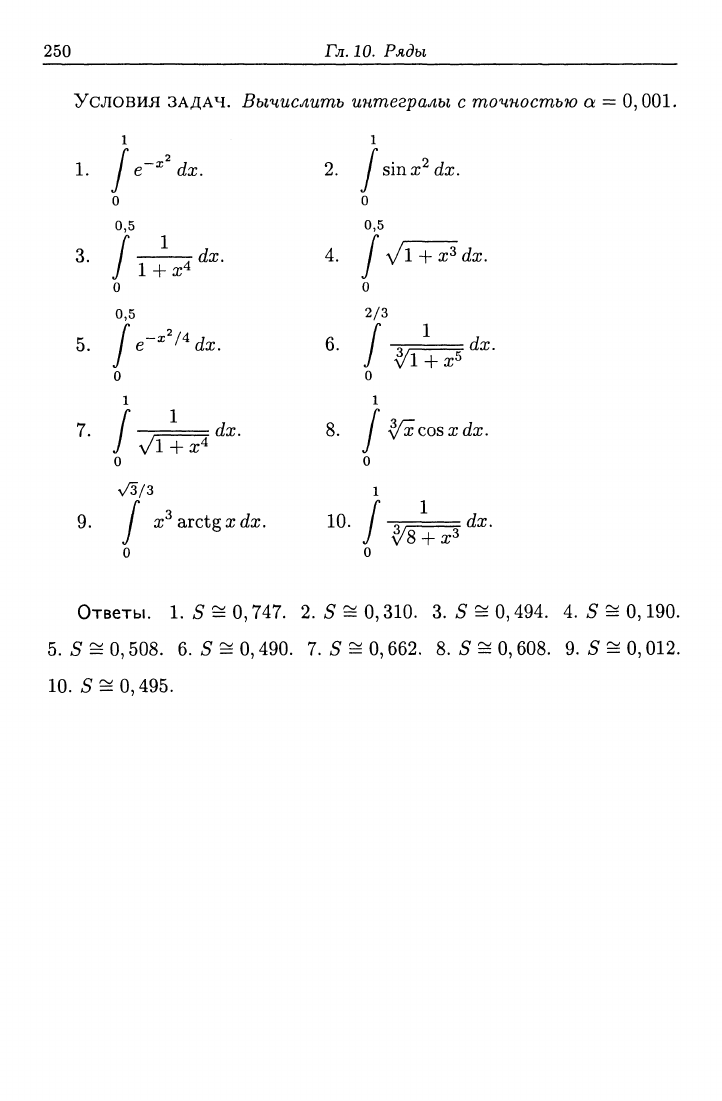
250 Гл.

10.

Ряды

Условия ЗАДАЧ. Вычислить интегралы с точностью а =

0,001.

1 1

/ е""^ dx. 2. / sinx'^dx.

о о

0,5 0,5

/ jdx. 4. / \/l + х^ dx.

х^

0,5 2/3

je^-'U..

6^ 1ш^'-

1 1

/ dx. 8. / \/xcosxdx.

J VTT^ J

0 0

уД/3 1

9. / x^SiTctgxdx. 10. / ^, dx.

J J V^T^

Ответы. 1.5^0,747. 2.5^0,310. 3.5 = 0,494. 4.5^0,190.

5.5^0,508. 6.5^0,490. 7.5^0,662. 8.5^0,608. 9.5^0,012.

10.

5^0,495.

Глава 11

ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ

При изучении темы ДИФФЕРЕНЦИАЛЬНЫЕ УРАВНЕНИЯ вы

познакомитесь с различными типами уравнений первого и второго

порядков и освоите методы их решения. Вы изучите линейные урав-

нения с постоянными коэффициентами, структуру их общего реше-

ния и методы его нахождения (метод Эйлера, метод подбора частных

решений, метод Лагранжа).

С помош;ью пакета РЕШЕБНИК.ВМ вы можете вычислить интег-

ралы, решить системы уравнений, продифференцировать найденные

решения и выполнить численные расчеты (например, при решении

задачи Коши), а также проверить полученные вами результаты.

11.1.

Понятие рехпения

ПОСТАНОВКА ЗАДАЧИ. Доказать, что функция у — у{х) удов-

лет^воряет дифференциальному уравнению F{x^y,y') = 0.

ПЛАН РЕШЕНИЯ.

Для доказательства того, что функция у = у{х) удовлетворяет

уравнению F{x^y^y') = О, достаточно вычислить производную

у'{х)^

подставить у(х) и у'{х) в это уравнение и убедиться в том, что полу-

чается тождество, т.е. F(x^y{x)^y'{x)) =

для всех допустимых х.

ПРИМЕР. Доказать, что функция у — —^х^

—

х'^

удовлетворяет

уравнению

/ 2 4

^уу -у ^х .

РЕШЕНИЕ. Имеем

, _ х(2х^ - 1)

Подставим у и у^ в левую часть уравнения и проведем необходимые

252

Гл.11.

Дифференциальные

уравнения

преобразования:

xf-y/^^^'^)

(-Щ£^]

-{х"" -х^) = х{2х^ -х) -хЧх^

х\

Получаем тождество

х"^

х"^.

Ответ. Функция у = —\/х^

—

х^ удовлетворяет заданному урав-

нению.

Условия ЗАДАЧ. Доказать, что функция у = у{х) удовлетво-

ряет дифференциальному уравнению f{x^y^y')

—

?/ = же~^/^, ху'= (1~ х'^)у.

у = x\J\

—

ж^, уу^ = X

—

2х^.

у = л/ж^

—

еж, (ж^ +

y'^)dx

—

2xydy = 0.

2/= e*s^^/^^ 2/'sina; = 2/l^l2/•

6. у = . , y-zy'= 6(l + x^y')•

y=-V2/z2-l,

+ у2+хуу'=0.

8. 2/= ГТ' У-Ж2/ =а(14-ж у ).

9. 2/ = е^+^^ + 2е^, у' - у = 2же^+^'.

10.

2/ = 2 + с\/1-ж2, (1-а:2)г/'-Ьж2/ = 2а:.

11.2.

Уравнения

с разделяющимися переменными

ПОСТАНОВКА ЗАДАЧИ. Найти интегральные кривые дифферен-

циального уравнения вида

E{x)F{y)dx = G{x)H{y)dy. (1)

11.2.

Уравнения с разделяющимися переменными

253

ПЛАН РЕШЕНИЯ.

В области, где G{x) 7^

и F{y) ф

разделяем переменные, т.е.

представляем уравнение (1) в виде

Вычислим интегралы в уравнении

^н.„_

{^ь)

/Ш-/

и преобразуем его к виду ^[х., у) = С.

Ответ записываем в таком виде: интегральные кривые опреде-

ляются уравнением (р{х,у)

С при всевозможных значениях С.

ЗАМЕЧАНИЕ. ЕСЛИ ОДНО ИЛИ

оба

уравнения

G{x) =

и F{y) =

имеют решения ж

Ж2,... иух, у2)

• • •?

то равенствах

xi,

Х2,... и

у = yi^y = У2,'

• -

нужно присоединить к ответу, так как они являются

интегральными кривыми дифференциального уравнения (1).

ПРИМЕР. Найти интегральные кривые дифференциального урав-

нения

бх dx

Qydy =

2x^2/

Зху^ dx.

РЕШЕНИЕ.

Перепишем исходное уравнение в виде

Зх(2

-К

у^) dx = 2у{х^ -h 3) dy.

(2)

Поскольку х^

> о и

2 -h 2/^

о, разделяем переменные, т.е.

представляем уравнение (2) в виде

Зх

^ 2у

—

•——г dy.

х2 + 3 2 -h 2/2

Вычислим интегралы в уравнении

/^^^^/з^^^-

Имеем

оХ

'^ т

/ 2

-ln(x^4-3) + Ci,

х2 +

254

Гл.11.

Дифференциальные

уравнения

22/

J.. ^,„,о , 2,

2 + 2/2

Следовательно,

^1п(х2 + 3)-1п(2 4-2/2) + Со,

где Со = С2

—

Ci.

Упростив это равенство, получим

(2 + 3/2)

Ответ. Интегральные кривые определяются уравнением

(х2 + 3)3

(2 + 2/2)

при всевозможных значениях С.

= С

Условия ЗАДАЧ. Найти интегральные кривые дифференциаль-

ных уравнений.

ydx

-\-

{1 + х'^)(1у = 0. 2. y' = tgxtgy.

у' у = -2х sec

2/.

4. у' + sin(x + у) = sin(a: - у).

у(1 + а:2)у' + 2:(1 + 2/2) =0. 6.

е""

dx - {1-^ еУ)ус[у = 0.

2/' = 2е^со8ж. 8. у^ = у1пу.

9. У = ^. 10.

2/'

-74=Т-

1 +

Ж^

Vx2 - 1

Ответы.

1п|2/| + arctga: = С. 2. sm?/cosx = C.

ж^-f?/sini/ + cosy = С. 4. ln|tg(2//2)| 4-2sina: = С

(а:2 + 1)(1 + у2)-а 6. 21п(1 + е^)-у2=.а

у = e^(cosx + sinx) + С. 8. 1п| In^/I -

= С.

9. ?/ = 1п(1 + х2) + а 10. 7/ = ln|a:-f \/ж2 - 1| + С.

11.3.

Однородные

уравнения 255

11.3.

Однородные уравнения

ПОСТАНОВКА

ЗАДАЧИ.

Найти интегральные кривые однородного

дифференциального уравнения первого порядка, т.е. дифференциаль-

ного уравнения вида

P{x,y)dx + Q{x,y)dy = 0, (1)

где Р{х,у) и Q{x,y) — однородные функции одинакового порядка,

т.е. P{tx,ty)=t''p[x,y) и Q{tx,ty) =

f'Qix^y).

ПЛАН РЕШЕНИЯ.

Преобразуем уравнение (1) к виду

»' = /(!). (!•)

Делаем подстановку у{х) = х z{x), где z{x) — новая неизвестная

функция. Тогда у' = z

-\-

х z' и уравнение (1') приводится к виду

Т.е. к уравнению с разделяющимися переменными.

Заметим, что подстановку у{х) ~ xz{x) можно делать сразу в

уравнении (1), не приводя его к виду (1').

Разделяем переменные в области, где f{z)

—

z ^ 0:

dz dx

f{z)-z X

Интегрируем полученное уравнение с разделенными перемен-

ными и делаем замену z{x) = у{х)/х. Записываем ответ.

ЗАМЕЧАНИЯ.

Если Z

=^ ZQ

— корень уравнения f{z) — z = О, то решением

уравнения (1) будет также у =

ZQX.

Интегральные кривые однородного уравнения можно искать и

в полярных координатах.

ПРИМЕР. Найти интегральные кривые дифференциального урав-

нения

, х^ + 2ху

— 5у'^

2х'^

—

Qxy

256 Гл.

11.

Дифференциальные

уравнения

РЕШЕНИЕ.

Преобразуем заданное уравнение к виду

14-2^-5

2-6-

(мы разделили числитель и знаменатель правой части заданного урав-

нения на ж^).

Делаем подстановку у = xz{x)^ где z{x) — новая неизвестная

функция. Тогда у' = z

-{-

xz' и уравнение приводится к виду

, 1 + 22 - 5^2

zx-^z = —-— ,

2-62;

т.е.

к уравнению с разделяющимися переменными.

В результате простых преобразований получаем

dz 1 + z^

X •=

dx 2 - 6z

Разделяем переменные {1

~{-

z^ ^

и х у^ 0):

2 - 6z , dx

az = —.

l-fz2 X

Интегрируя, получаем

2arctg z - 31n(l -f z^) = In \x\ + C.

Заменяя z на y/x., получаем

2arctg ~ - 31n (1 4- ^ I - In \x\ = C.

X \

Ответ. Интегральные кривые определяются уравнением

X \Х\^

при всевозможных значениях С.

11.4. Линейные уравнения l-zo порядка 257

Условия ЗАДАЧ. Найти интегральные кривые дифференциаль-

ных уравнений.

X X

X cos —

-\-

(х - у

cos

—) dx = 0. 5. (ж^ -f 2ху) dx

-\-

ху dy = 0.

X \ X/

6. xy'ln f

—

j =ж 4-2/1п

( — 1

. 7.

2/б^а:

+ (2у^

—

ж)б?г/= 0.

8. {Ау'^+х'^)у' =

XT/.

9.xi/'sin f-• j-bx = ysin f-j .

10.

xy + y^ = (2^2 +

Ж2/)

y'.

Ответы.

e-y/^+ln|a:| = a 2. же^^/^^С.

e^/y + lnlxl =a 4. Inlxl+sin^ =a

1п|ж +

2/|

+ —^ = C 6. Inx-^fln^-l) =a

у|

+ 1пы

= а 8. 1пы^^

11.4.

Линейные уравнения 1-го порядка

ПОСТАНОВКА ЗАДАЧИ. Решить задачу Коши для уравнения

у'Л-р{х)у

= q{x) (1)

с начальным условием

у{хо)

2/0.

(1')

ПЛАН РЕШЕНИЯ.

1-й способ.

Запишем соответствующее однородное линейное уравнение:

у'+р{х)у

= 0. (2)

258 Гл.

11.

Дифференциальные

уравнение

Это уравнение с разделяющимися переменными.

Разделяя переменные и интегрируя, получим общее решение

однородного уравнения (2)

у = С ехр Llpix)dx\. (3)

Применяем метод вариации произвольной постоянной:

а) ищем решение неоднородного уравнения (1) в виде (3), считая

С неизвестной функцией ж, т.е. полагая С = С{х)\

б) подставляем в уравнение (1) у и у'^ определяемые из соотноше-

ния (3), где С = С{х). Из полученного дифференциального уравнения

определяем функцию С{х).

Таким образом, общее решение неоднородного уравнения (1)

получаем в виде

—

С[х) ехр {— 1 р{х) dx >. (3')

Здесь С{х) содержит произвольную постоянную Со.

Используя начальные условия (1'), находим значение Со и по-

лучаем решение поставленной задачи Коши.

Записываем ответ в виде у — ^{х).

2-й способ.

Ищем решение уравнения (1) в виде

у = u{x)v{x), (4)

где и

V — неизвестные функции х.

Уравнение (1) принимает вид

u'v -Ь uv' + p{x)uv = q{x). (5)

Поскольку теперь мы имеем две неизвестные функции, а урав-

нение, которому они должны удовлетворять, только одно, то еще одно

уравнение мы можем принять произвольно, лишь бы оно не сужало

множество решений у.

Пусть одна из функций (например, и{х)) удовлетворяет уравне-

нию

и'-\-р{х)и = 0. (6)

11.4. Линейные уравнения 1-го порядка 259

Тогда уравнение (5) примет вид

v'u = q[x). (7)

Решая уравнение (6) (с разделяющимися переменными), находим li, не

равное тождественно нулю, чтобы не сужать множество решений у.

Подставляем и[х) в уравнение (7) и решаем его относительно v.

Записываем общее решение уравнения в виде у{х) = u{x)v{x).

6. Используя начальные условия (1'), получаем решение постав-

ленной задачи Коши.

Записываем ответ в виде у

—

(f{x).

ПРИМЕР. Найти решение задачи Коши для уравнения

X Х^

с начальным условием

2/(1)-1.

РЕШЕНИЕ.

1-й способ.

Записываем соответствующее однородное линейное уравнение:

2/'

- ~

= 0.

Это уравнение с разделяющимися переменными.

Разделяя переменные и интегрируя, получаем общее решение

однородного уравнения

у = Сх.

Применяем метод вариации произвольной постоянной:

а) ищем решение неоднородного уравнения (8) в виде

у ^ С{х)х,

где С{х) — неизвестная функция х\

б) подставляя в уравнение (8)

у = С{х)х и у' = С\х)х + С{х),