Зимина О.В., Кириллов А.И., Сальникова Т.А. Высшая математика. Решебник

Подождите немного. Документ загружается.

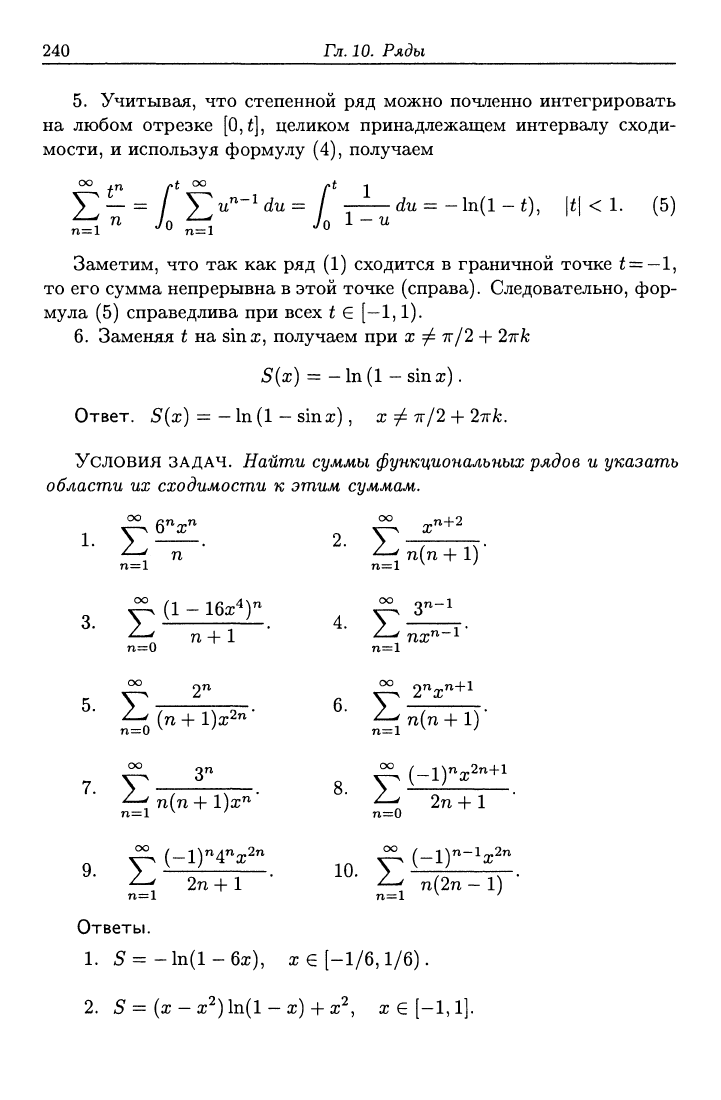
240 Гл.

10.

Ряды

Учитывал, что степенной ряд можно почленно интегрировать

на любом отрезке

[0,t],

целиком принадлежащем интервалу сходи-

мости, и используя формулу (4), получаем

У2-= yZu'^-'du^ ^^—du =

-\n{l-t),

\t\<l. (5)

^^1 ^ Jo „^1 Уо 1 - ^

Заметим, что так как ряд (1) сходится в граничной точке t =

—1,

то его сумма непрерывна в этой точке (справа). Следовательно, фор-

мула (5) справедлива при всех t G

[—1,1).

6. Заменяя t на sin

ж,

получаем при х ф -к 12 + 27г/с

S{x) =

—

(1 —

sin х).

Ответ. S{x) = -ln(l - sinx), хф

-KJI

+ 27гА;.

Условия ЗАДАЧ. Найти суммы функциональных рядов и указать

области их сходимост^и к этим суммам.

°° п+2

6"х" 2 V ^

п=1

у^ (1 - 16а;4)"

п=0

^ 2"

^^{п + 1)х^--

°° on

У"

^ п(п+1)х"'

п=1 ^ '

-^ (-1)"4"х2"

^ п(гг4-1)*

п=1 ^ '^

оо оп-1

4. У^.

ПХ"

п=1

ОО г)П„П+1

- (_1)п^2п+1

• ^ 2п + 1 '

п=0

10^

(-1)^-^Ж^^

2п + 1 ' ^^' ^^ п(2п - 1)

п=1 п=1 ^ ^

Ответы.

5=-1п(1-бж),

ж G

[-1/6,1/6).

S={x-x'^)ln{l-x) + x^,

XG[-1,1].

10.12.

Вычисление

суммы

рлда почленным

дифференцированием

241

5 = -|ln^-^, а: G (-00,-3]и(3,+оо).

3 X

5=-— In г—, xG (-с?о,-\/2)и(\/2,+оо).

2 х^

6. 5 = (1 - 2х)

1п(1

- 2х) + 2х, ЖЕ [-1/2,1/2].

'5 = -^1^-у^ + |' хе(-оо,-3]и[3,4-оо).

8. 5=arctga:, a:G[-l,l].

9.5=^^-1 .б[-1А1/2].

10.

5 = 2a:arctga:-ln(H-a:2), ЖЕ[-1,1].

10.12.

Вычисление суммы ряда

почленным дифференцированием

ПОСТАНОВКА ЗАДАЧИ. Найти сумму функционального ряда вида

оо

n=fc

и указать област,ь сходимости ряда к эт.ой сумме.

ПЛАН РЕШЕНИЯ.

Находим область сходимости ряда.

По признаку Коши интервал сходимости определяется неравенст-

вом

1/(^)1

< 1-

Если /(х) = ±1, ряд расходится (не выполнено необходимое условие

сходимости). Следовательно, область сходимости определяется нера-

венствами

— 1

< f{x) < 1.

242 Гл. 10. Ряды

Делаем в исходном ряде замену f{x) = t и записываем его в

виде суммы двух рядов

^пГ + Ь^Г.

п=к п=к

Следовательно, достаточно найти суммы рядов

оо с»

п—к п=к

Известна формула для суммы членов бесконечно убывающей

геометрической прогрессии

со

,]^

n=fc

Кроме того, имеем очевидное равенство

сх) оо со ,

п=к п=к п~к

Учитывая, что степенной ряд можно почленно дифференциро-

вать в любой точке интервала сходимости, и используя формулу (1),

получаем

ОС

rJ °^ г1 +к

^ dt^^ dt 1-t' ^ ' ^

n=k n=k

6. Вычисляем производную и делаем замену t на f{x).

Записываем ответ: сумму ряда и область его сходимости.

ЗАМЕЧАНИЕ. ЕСЛИ ряд имеет вид

оо

J2{n'

+ c)f{xr,

п=к

ТО вычисляем сумму трех рядов, причем при вычислении суммы ряда

E"VW"

п—к

10.12.

Вычисление

суммы

ряда почленным

дифференцированием

243

применяем теорему о почленном дифференцировании степенного ря-

да дважды.

ПРИМЕР. Найти сумму ряда

оо

ji -г u;u;

n=0

и указать область сходимости ряда к этой сумме.

РЕШЕНИЕ.

Находим область сходимости ряда.

По признаку Коши интервал сходимости определяется неравенст-

вом |ж^| < 1. Отсюда

— 1

< ж < 1. В граничных точках х = ±1 ряд

расходится, так как не выполнено необходимое условие сходимости.

Следовательно, ряд сходится в интервале ( — 1,1).

Делаем в исходном ряде замену х'^ = t и записываем его в виде

суммы двух рядов

сю оо

S{t) = б ^ г + ^ nt" = 6Si{t) + S2{t).

n=0 n=0

Следовательно, достаточно найти суммы рядов

оо оо

n=0 n=l

Используем формулу для вычисления суммы членов бесконечно

убывающей геометрической прогрессии:

оо

Е^'

= г^' w<i. (2)

п=0

Следовательно, Si{t) = при всех t G (—1,1).

Кроме того, имеем очевидное равенство

оо оо оо J

п=1 п=1 п=1

244 Гл.

10.

Ряды

Учитывая, что степенной ряд можно почленно дифференциро-

вать в любой точке интервала сходимости, и используя формулу (2),

получаем

n=l п~1 ^ '

Таким образом.

S{t) =

63г{Ь) +

S,{t) = Y^ + (Y^ ^ W=W'

^ ^"^' ^^'

Заменяя t на

x'^

получим

—

5ж^

Ответ. 5(a:)-—--^, же(-1,1).

Условия ЗАДАЧ. Найти суммы функциональных рядов и указать

области их сходимости к этим суммам.

оо

^па;"+Ч 2. ^п2"х".

П=1 П=1

ОО оо

5Z("+i)^'"^'- 4- Е

п=1 п=1

3П-1

п=0 п=1

5. ^viLli2^1.f2^. 6. ^n^x-i.

n=0 n=l

00 00

n=0 n=l

9. ^n(n + 2)x". 10. ^n(a:^ + l)"-\

n=l n=l

10.13.

Ряд Тейлора 245

Ответы.

х^ 2х

1-5 = 7г^^ -е(-1Д)- 2-5 = 7rfi:;^>-e(-i,^)-

_9_

3-'5 = 7Т—3W' ^e(-i.i)- 4.5 = ^——^, хе(-з,з).

^•^ = Ц^^' а:е(-1,1).

10.5

= ^, xG(-^,o).

10.13.

Ряд Тейлора

ПОСТАНОВКА ЗАДАЧИ. Разложить функцию f{x) в ряд Тейлора

по степеням х

[XQ

= 0).

ПЛАН РЕШЕНИЯ.

Преобразуем функцию f{x) к виду, допускающему использова-

ние табличных разложений е^, sina:, cos

ж,

(1 + ж)"^, 1п(1 + х).

Находим разложение функции в ряд Тейлора, используя таблич-

ные разложения, сложение (вычитание) рядов, умножение ряда на

число.

Определяем область сходимости полученного ряда к функ-

ции /(ж).

ЗАМЕЧАНИЕ. ЕСЛИ необходимо разложить функцию в ряд Тейлора

по степеням ж

—

жо, сначала делаем замену переменной t = ж

—

жо,

находим разложение по степеням t и возвращаемся к переменной ж.

ПРИМЕР.

Разложить функцию

2 -

- ж2

в ряд Тейлора по степеням ж (жо = 0).

246 Гл.

10.

Ряды

РЕШЕНИЕ.

Чтобы использовать табличные разложения, разложим данную

функцию на элементарные дроби:

1 1

2-х~х'^ 1- X '

х-\-2'

Используя табличное разложение

1 °°

__ = 1 +1 +1^ + ... + Г + ... - ^ Г, te (-1,1),

п=0

1 °^

-— = $]x^ xG(-i,i),

1 — X ^—'

п=0

^^1 1 _ 1 ^ (-irx- ^ -

{-1Гх-

а:е(~22)

. ^ 9.

1-4-^/9

9 Z^ 9.П Z^ 9.П+1 ' -^^l ^'^^

п=0

получим

1 -.т ~

п=0

2 +

2 1 + ж/2 2 ^ 2" ^2

' п=0 п=0

Таким образом,

_ ^ _ ^2 ~ 2-^

^ "^

9пН ^ •

Областью сходимости полученного ряда является пересечение

вышеуказанных областей сходимости, т.е.

(—1,1)

(—2,2)

= (—1,1).

n=0 ^ ^

Условия ЗАДАЧ. Разложить функции в ряды Тейлора

[XQ

= 0).

^ 2. 1п(1-2:-20х2).

±.

— ж — ж-^

/ '^\

sin(x + -).

3 + 2ж'

же2^^+1.

6. ^16 4-х.

^27-X*

9. In(12x2-h7x + l). 10. соз^Зх.

10.14.

Приблиоюепные

вычисления

помощью

рядов

247

Ответы.

Е(^

У?)-". хе(-2,2).

п=0

оо

Зп+1 2^"^-'-

(_1)п-14п_5п

ж'%

X е

п=1

"5'5

Е7^^--

^Е^^-> .е(-.,..).

,g>(-l)"(2n-l)!!.,,„^,

' ^-^

п!2"32"+1

п=1

п=0

'' '

а;'"+\

ж €(-3,3).

^"-^^

Z-^

Чп+1

(-!&

ж G

п=0

"2'2

• ^^|^В-'г-'^'"•:•!;""''-'• -<^|-'».1Ч.

п=2

2П

7. е^—х2^+\ ж€(-оо,+оо).

п=0

'•

^E'"!..i!r-V .е(-2Г,.П.

' ^

п!34^+1

п=1

Е(-1)

4»

„ /11

\ 4 4

\П(У2П

( —1)"6

10.14.

Приближенные вычисления

с помощью степенных рядов

ПОСТАНОВКА ЗАДАЧИ. Вычислить интеграл

f{x) dx

/•

с т,очност,ъю

а,

г(9е

f{x)

разлоэюима

степенной ряд, имеющий ра-

диус сходимост,и

> Ь.

248 Гл.

10.

Ряды

ПЛАН РЕШЕНИЯ. Практические вычисления обычно сводятся

суммированию того

или

иного числового ряда.

данном случае

та-

кой

ряд

получается, если разложить подынтегральное выражение

степенной

ряд и

проинтегрировать

его

почленно.

Разлагаем подынтегральную функцию

степенной

ряд по

сте-

пеням

X^Cnx"",

n=0

и определяем

его

область сходимости.

Степенной

ряд

можно интегрировать почленно

по

любому

от-

резку, принадлежащему интервалу сходимости. Поэтому, интегри-

руя почленно полученный

ряд и

используя формулу Ньютона-Лейб-

ница, получаем

f{x)

dx=

Y^^"^"

= Y^Cn -—т.

Вычисляем сумму числового ряда

заданной точностью (оце-

нивал остаток ряда).

ЗАМЕЧАНИЕ.

ЕСЛИ

разложить подынтегральную функцию в ряд

не

по

степеням

ж, а по

степеням

ее

—

6/2, то ряд

будет сходится быст-

рее,

т.е. для

обеспечения заданной точности может потребоваться

меньше слагаемых, однако

итоге вычисления оказываются более

сложными.

ПРИМЕР. ВЫЧИСЛИТЬ интеграл

0,1

cos(lOOx^)

/•

с точностью

а =

о, 001.

РЕШЕНИЕ.

Разлагаем подынтегральную функцию

в ряд

Тейлора

по

степе-

10.14. Приближенные вычисления с

помощью

рядов 249

ням х:

/1ПП 2х , (102^2)2 (102а:2)4 (lO^rr^)^

^/ ^ (2п)! ^^ ^ (2п)! •

п=0 ^ ^ п=0 ^ ^

Разложение справедливо при всех х.

Интегрируем почленно полученный ряд:

0,1 0,1 0,1

о о '^~^ ^~^ о

п=0 ^ ^ "J п=0 ^ /

3. Оценим остаток

ряда.

Так как ряд знакочередующийся,

1 1

dn = 77771 , 1\/г> м > ^п+1 =

" 10(4n + l)(2n)! "^' 10(4п + 5)(2п + 2)!

и limn->oo ttn = О, то справедливо неравенство

\Rn\

< dn+l =

10(4n + 5)(2n + 2)!

Для вычисления интеграла с заданной точностью достаточно

взять два члена ряда, так как

Производя вычисления, получаем

0,1

I cos(100x2) dx^^- Y^T^ = 0,090.

0,1

Ответ. 1 со8(100ж2) dx ^ 0,090 ±

0,001.