Журбенко Л.Н., Никонова Г.А., Никонова Н.В., Нуриева С.Н., Дегтярева О.М. Математика в примерах и задачах
Подождите немного. Документ загружается.


351
р
1
р
2
р
3
q
0 1 0 1
0 0 0 1
Запишем нормальную дизъюнктивную форму, используя стро-
ки с q = 1:
q = (p
1
∧ p
2
∧ p
3
) ∨ (
p
1
∧ p
2
∧ p
3
) ∨ (
p
1
∧
p
2
∨ p
3
) ∨
∨ (
p
1
∧ p
2
∧
p
3
) ∨ (
p
1
∧
p
2
∧
p
3
).
Упростим ее, используя равносильности 2–4, 7, 9 ОК,
разд. 37.2:
q = (p
1
∧ p
2
∧ p
3
) ∨ [
p
1
∧ ((p
2
∧ p
3
) ∨ (
p
2
∧ p
3
) ∨
∨ (p
2
∧
p
3
) ∨ (
p
2
∧
p
3
))] = (p
1
∧ p
2
∧ p
3
) ∨ [
p
1
∧ (p
3
∧
∧ (p
2
∧
p
2
)) ∨ (
p
3
∧ (p
2
∨
p
2
))] = (p
1
∧ p
2
∧ p
3
) ∨
∨ [
p
1
∧ (p
3
∨
p
3
))] = (
p
1
∧ p
2
∧ p
3
) ∨
p
1
= (p
1
∨
p
1
) ∧
∧ ((p
2
∧ p
3
) ∨
p
1
) =
p
1
∨ (p
2
∧ p
3
).
Из последней формулы следует краткая формулировка условий,
при которых поход состоится: а) не будет дождя или б) соберется
больше пяти человек с палаткой.
Задача 3. Построить булеву функцию, отражающую работу
устройства, которое состоит из трех узлов, пропускающих некото-
рый сигнал, если его пропустило большинство узлов. Если сигнал
прошел через конкретный узел а
i
, в таблице истинности имеем 1,
в противном случае — 0.
Решение: Устройство реализует «высказывание» А(a
1
, a
2
, a
3
),
таблица истинности которого имеет вид:
a
1
a
2
a
3
А(a
1
, a
2
, a
3
)
1 1 1 1
1 1 0 1
1 0 1 1
1 0 0 0
0 0 0 0
0 0 1 0
0 1 0 0
0 1 1 1
При этом функция А(a
1
, a
2
, a
3
) может быть представлена в
виде
А(a
1
, a
2
, a
3
) = (
a
1
∧ a
2
∧ a
3
) ∨ (a
1
∧
a
2
∧ a
3
) ∨
∨ (a
1
∧ a
2
∧
a
3
) ∨ (a
1
∧ a
2
∧ a
3
).

352
Задача 4. Истинны или ложны следующие предикаты, если
х, у ∈ R:
а) ∀х (х
2
> x ⇔ x > 1 ∨ x < 0); б) ∀x, y (х
2
≠ 2y
2
).
Решение: а) решение неравенства х
2
- х > 0 ⇔ x(x - 1) > 0
находится методом интервалов:
т.е. x ∈ (-∞, 0) ∪ (1, +∞), поэтому предикат тождественно истин-
ный;
б) уравнение х
2
= 2у
2
записывается в виде х = ±
2
у, т.е. для
точек (х, у), удовлетворяющих равенству х ±
2
у = 0, не выполня-
ется х
2
≠ 2у
2
, т.е. предикат ложный.
Задачи для самостоятельного решения
1) Составить таблицы истинности для следующих формул:
а) (а
1
⇒ а
2
) ∨
a
3
; б) (а
1
∧
a
2
) ⇒ (а
2
∨ а
3
); в) (
a
1
∧ а
2
) ∨
∨ (а
2
⇒ а
1
); г) (а
1
⇒ а
2
) ∨ (а
1
⇒ (а
2
∧ а
1
).
2) С помощью таблиц истинности доказать:
а) равносильности формул ОК, разд. 37.2; б) формулы погло-
щения а ∨ (а ∧ b) = а; а ∧ (а ∨ b) = а.
3) Упростить, пользуясь равносильностями ОК, разд. 37.2:
а) (а ∧ b) ∨ (а ∧
b
); б) (а ∨ b) ∧ (а ∨
b
);
в) р
2
∨ (р
1
∧
p
2
∧ р
3
); г) (р
1
∧
p
2
∧ р
3
) ∨ (
p
2
∧ р
3
∧
p
1
);
д) (р
1
⇒ р
2
) ∧
p
2
.
4) По таблицам истинности построить дизъюнктивные нор-
мальные формы для F
1
(p
1
,
p
2
, p
3
), F
2
(p
1
,
p
2
, p
3
), F
3
(p
1
,
p
2
, p
3
) и
упростить их.
р
1
p
2
р
3
F
1
F
2
F
3
1 1 1 1 0 0
1 0 1 0 1 0
1 1 0 0 0 1
1 0 0 0 0 1
0 1 1 1 1 1
0 0 1 0 1 1
0 1 0 0 0 0
0 0 0 0 0 0

353
5) Истинны или ложны следующие предикаты, если х, у ∈ R:
а) Р = ∀х∃у(х + у = 3); б) P = ∃y∀x(х + y = 3);
в) P = ∃x, y(х > y > 0 ∧ x + y = 0);
г) P = ∀x, y(х < y) ⇔ ∃z(x < z < y);
д) P = ∀x(х > 2 ∧
x > 3
⇔ 2 < x ≤ 3).
38. ГраФы
опорный конспект № 38
38.1. Основные понятия и способы задания графов
О: Граф G = {V, E}, V = {a
1
, a
2
, ..., a
n
} — вершины,
Е = {(a
i
, a
j
)}, i,
jn= 1,
— ребра, l
ij
= (a
i
, a
j
) инцидентно a
i
, a
j
G — ориентированный граф, если (a
i
, a
j
), i,
jn= 1,
, — упорядо-
ченные пары из V
О: Мультиграф — граф, имеющий кратные ребра
О: Степенью вершины графа G называется число ребер, инци-
дентных а
Граф изображается диаграммой или задается матрицей смеж-
ности (δ
ij
) n-го порядка, в которой δ
ij
равно числу ребер, инцидент-
ных a
i
и a
j
для неориентированниго графа
38.2. Маршруты, цепи и циклы
О: Маршрут М в графе G = {V, E} ⇔ М = {l
ij
}, где два сосед-
них ребра имеют общую инцидентную вершину
Цепь — маршрут М, у которого все ребра различны. Простая
цепь — маршрут М, у которого все вершины, кроме, быть может,
первой и последней, различны
Цикл — цепь, в которой начальная и конечная вершины совпа-
дают
О: Граф G связный, если любая пара его вершин соединяется
цепью
О: Эйлеров граф ⇔ связный неориентированный мультиграф,
для которого существует цикл, содержащий все ребра
Т: Связный неориентированный мультиграф эйлеров т. и т.т.,
когда степени его вершин четны
38.3. некоторые классы графов
О: Дерево — связный граф без циклов, лес — несвязный граф
без циклов

354
Любая цепь в таком графе — простая. Любые две вершины де-
рева связаны одной и только одной цепью
О: Остовом графа G = {V, E} называется дерево H = {V, E*},
E* ⊆ E
О: Двудольный граф G = {V, E} ⇔ V = V
1
+ V
2
, причем каж-
дое ребро имеет один конец из V
1
, другой — из V
2
38.4. Понятие об автоматах, их задание графами
О: Конечный автомат S = {A, Q, V, δ, λ},
A = {a
1
, a
2
, ..., a
m
} — входной алфавит,
V = {v
1
, v
2
, ..., v
l
} — выходной алфавит,
Q = {q
1
, q
2
, ..., q
n
} — алфавит состояний,
q
k
= δ(q
i
, a
j
) — функция переходов,
v
r
= λ(q
i
, a
j
) — функция выходов
Наглядным способом задания автомата является ориентирован-
ный мультиграф (граф переходов)
Задачи к разд. 38
Задача 1. Неориентированный граф задан списком ребер (a, b),
(a, c), (b, c), (c, d), (d, e). Построить диаграмму и записать мат-
рицу смежности. Привести пример маршрута, не являющегося
цепью, и цикла в этом графе.
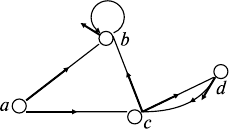
Решение: Диаграмма графа имеет, например, вид, представлен-
ный на рис. 38.1.
Рис. 38.1
Запишем матрицу смежности пятого порядка (δ
ij
), в которой
элемент (δ
ij
) равен числу ребер, инцидентных вершинам a
i
, a
j
:
0 1100
10100
11010
00101
00010
.
355
Пример маршрута, не являющегося цепью: acbcde, пример цик-
ла: abca.
Задача 2. Построить ориентированный граф по матрице смеж-
ности:
0110
0110
0001
0010
.
Каковы степени вершин графа?
Решение: Обозначим вершины графа через a, b, c, d. Поскольку
элемент δ
ij
соответствует числу ребер с началом в a
i
и концом в a
j
,
имеем следующий список ребер:
(, ),ab
(,),ac
(, ),bb
(, ),bc
(, ),cd
(,)dc
соответственно. Можем построить диаграмму (рис. 38.2).
Рис. 38.2
Определим степени вершин: S
a
= 2, S
b
= 3, S
c
= 4, S
d
= 2.
Задача 3. Расстояние между потребителями электроэнергии А,
Б, Г, Д, Е в десятках километров дано в табл. 38.1. Требуется по-
строить сеть линий электропередач так, чтобы количество затра-
ченных проводов было минимальным и можно было передать
энергию из каждого города в любой другой.
Решение: Построим граф G
6
, имеющий шесть заданных вершин,
соединенных между собой.
Число ребер соответствует числу элементов в таблице (матрице)
расстояний, лежащих выше (ниже) главной нулевой диагонали.
Около каждого ребра указано расстояние между потребителями.
Эти величины называют весом соответствующего ребра. Всего
можно построить 6
6-2
= 1296 деревьев, соединяющих данные
пункты. Ищем дерево W, имеющее наименьшую суммарную длину
ребер. Число ребер Q графа W можно определить, зная γ — цикло-
матическое число графа G, число вершин n, число ребер m, число

356
компонент k графа G
6
: γ = m - n + k = 15 - 6 + 1 = 10, Q =
= m - γ = 15 - 10 = 5 (ребер).
Строим граф W. Для этого:
1) выбираем ребро наименьшей длины l(Д, Е) = 1;
2) среди оставшихся выбираем ребро меньшей длины: l(Г, Д) = 2;
3) из оставшихся ребер выбираем ребро наименьшей длины, не
образующее циклов с уже выбранными: l(В, Г) = 3;
4) из оставшихся ребер выбираем ребро l(Б, Д) = 6, так как
оно не образует циклов с уже выбранными;
5) по аналогии с п. 4 выбираем ребро l(А, Г) = 6.
На рис. 38.3 остовное дерево W выделено жирной линией. Таким
образом, суммарная длина графа L = 1 + 2 + 3 + 6 + 6 = 18.
Задачи для самостоятельного решения
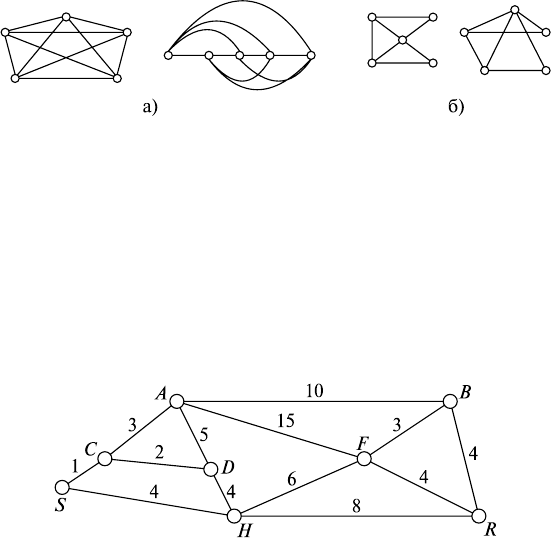
1) Написать матрицы смежности для следующих графов
(рис. 38.4):
Рис. 38.4
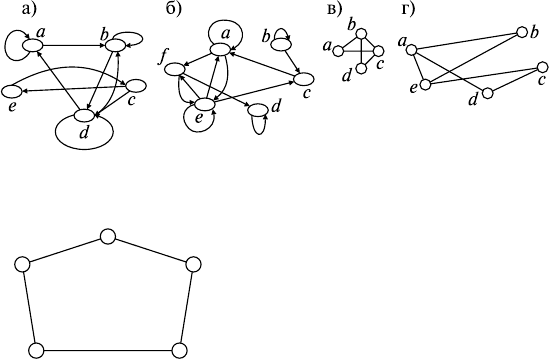
2) По матрице смежности постройте граф:
Рис. 38.3
357
а)
11000
01010
00011
11010
00100
;
б)
1 00011
0 11000
1 00000
000100
101011
000110
;
в)
0110
1011
1101
0110
;
г)
01011
1 0001
00011
10100
11100
.
3) Доказать, что на рис. 38.5, а и б изображен один и тот же
граф.
Рис. 38.5
4) Граф с n ≥ 2 вершинами называется полным, если каждая
его вершина соединена ребром с каждой из остальных вершин.
Каково должно быть число вершин полного графа, если известно,
что этот граф эйлеров?
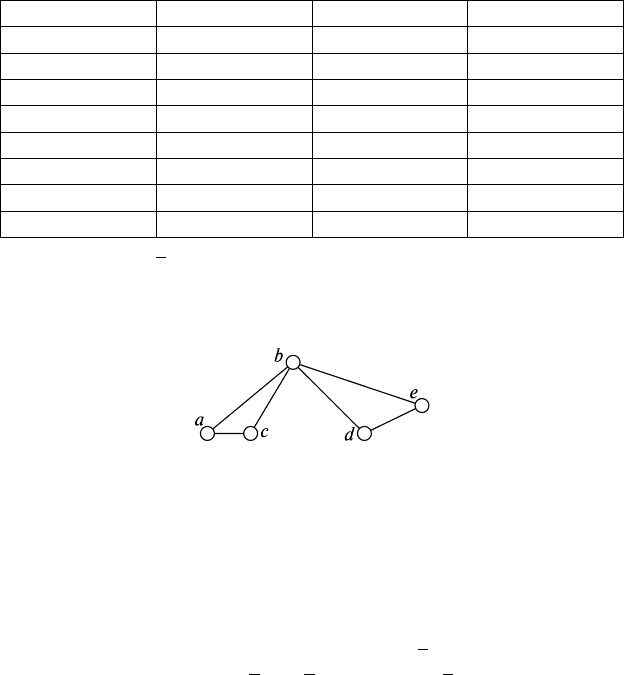
5) Расстояние между соседними пунктами на графе обозначено
цифрой над ребром, соединяющим эти пункты (рис. 38.6). Выбрать
кратчайший маршрут из S в R так, чтобы побывать в каждом пункте
один раз.
Рис. 38.6

358
6) Имеется 5 предприятий, из них каждое сотрудничает только
с двумя. Возможно ли это? Показать на графе.
7) Доказать, что в двудольном графе цикл всегда имеет четное
число ребер.
8) Пусть имеется 18 команд, желающих участвовать в турнире.
С помощью графа — дерева спланируйте этапы соревнований:
1/16, 1/8, 1/4, 1/2, финал. Каким должно быть исходное число
команд, для того чтобы на любом этапе соревнований каждая ко-
манда, дошедшая до этого этапа, участвовала в игре?
9) Из пункта А в пункт В выехали пять машин одной марки
разного цвета: белая, черная, красная, синяя, зеленая. Черная едет
впереди синей, зеленая — впереди белой, но позади синей, крас-
ная — впереди черной. Каков порядок их движения?
варианты контрольной работы
Вариант № 1
1. Записать таблицу истинности для формулы
qppp=∨⇔().
12 3
2. По табл. 1 истинности построить дизъюнктивную нормаль-
ную форму и упростить ее:
Таблица 1
р
1
р
2
р
3
F(p
1
, p
2
, p
3
)
1 1 1 0
1 0 1 0
1 1 0 0
1 0 0 1
0 1 1 0
0 0 1 1
0 1 0 0
0 0 0 0
Ответ:
Fp pp=∧ ⇔
21 3
().
3. Привести пример эйлерова графа.
4. Чему равно выражение (a ∧ b) ∨ c ∨ a ∧ b ∨ a при с = 0?
Ответ: а.
Вариант № 2
1. Проверить равносильность (a ∧ b) ∧ c = a ∧ (b ∧ c) с по-
мощью таблиц истинности.
359
2. По табл. 2 истинности построить дизъюнктивную нормаль-
ную норму и упростить ее:
Таблица 2
р
1
р
2
р
3
F(p
1
, p
2
, p
3
)
1 1 1 0
1 0 1 1
1 1 0 0
1 0 0 1
0 1 1 0
0 0 1 0
0 1 0 0
0 0 0 0
Ответ: p
1
∧
p
2
.
3. Записать матрицу смежности для неориентированного графа,
заданного диаграммой:
Рис. 38.7
4. Чему равно выражение (a ∨ b) ∧ c ∨ a ∧ (b ∨ с) ∧ b при
b = 1? Ответ: c ∨ a.
ответы к разд. 37, 38
37. Логические исчисления
3) а) а; б) а; в) р
2
∨ ( р
1
∧ р
3
); г)
p
2
∧ р
3
; д) р
1
∨ р
2
;
4) а) р
2
∧ р
3
; б) р
3
∧ (
p
2
∨
p
1
); в) р
1
⇔
p
3
; 5) а) истинен
(Р = 1); б) 0; в) 0; г) 1; д) 1.
38. Графы
1) а)
0010
0011
1101
0110
;
г)
11100
00110
01000
00001
00000
;
д)
0200
0210
0011
0010
;
2)
4) n — нечетное число. Указание: Использовать критерий эйле-
рова графа; 5) SCADHFBR;
6)
8) 16; 9) 1 — красная, 2 — черная, 3 — синяя, 4 — зеленая, 5 —
белая. Указание: Строится орграф для отношения: х едет сзади y.
