Журбенко Л.Н., Никонова Г.А., Никонова Н.В., Нуриева С.Н., Дегтярева О.М. Математика в примерах и задачах

Подождите немного. Документ загружается.

311

Задача 2. Бросают три монеты одновременно. Случайное собы-

тие А состоит в появлении герба только на одной монете. Описать

пространство элементарных событий Ω и определить, сколько

элементарных событий содержится в Ω и входит в случайное со-

бытие А.

Решение: Обозначим через r выпадение герба, а через p — выпа-

дение решки на одной монете. Пространство элементарных собы-

тий Ω включает следующие события: (r, r, r), (r, r, p), (r, p, r),

(p, r, r), (r, p, p), (p, r, p), (p, p, r), (p, p, p), т.е. включает восемь

элементарных событий. Случайное событие А включает элемен-

тарные события (r, p, p), (p, r, p), (p, p, r), т.е. содержит три со-

бытия.

Задача 3. В урне 5 черных и 6 белых шаров. Из нее случайным

образом вынимают 4 шара. Случайное событие А состоит в том, что

из четырех шаров два — белые. Описать пространство элементар-

ных событий, определить их число и число элементарных событий,

входящих в А.

Решение: Пространство элементарных событий Ω состоит из ω

каждое из которых есть выбор четырех шаров из 11, их число n =

= C

= 330. Случайное событие А включает те ω

, для ко-

торых два шара белые. Это значит, что из четырех вынутых ша-

ров — 2 белых и 2 черных. Два белых шара из шести белых в урне

выбираем С

способами, два черных — С

способами. Тогда в со-

бытие А входит m = C

⋅⋅

150 элементар-

ных событий.

Задача 4. Из таблицы случайных чисел наугад выбраны два чис-

ла. Событие А — выбрано хотя бы одно простое число, событие В —

выбрано хотя бы одно четное число. Что означают события АВ и

А ∪ В?

Решение: Событие АВ означает наступление и события А, и со-

бытия В, т.е. из двух выбранных чисел одно — простое, другое —

четное. Событие А ∪ В означает наступление или события А, или

события В, т.е. или хотя бы одно из двух выбранных чисел простое,

или хотя бы одно из них — четное. В последнем случае оба числа

могут быть простыми или четными, или одно — простое, другое —

четное.

312

Задачи для самостоятельного решения

1) Из 10 роз и 8 георгинов нужно составить букет, содержащий

2 розы и 3 георгина. Сколько можно составить различных буке-

тов?

2) В колоде 36 карт, из них 4 туза. Сколькими способами можно

сдать 6 карт так, чтобы среди них было 2 туза?

3) Сколько сигналов можно составить из 10 флажков различ-

ного цвета, взятых по два?

4) Сколькими способами можно расставить на полке 6 книг?

В задачах 5)–7) описать пространство элементарных событий Ω

и определить, сколько элементарных событий содержится в Ω и

входит в случайное событие А.

5) Бросают игральную кость. Событие А — на верхней грани

появится четное число.

6) Бросают 4 монеты. Событие А — только на двух монетах

появится герб.

7) В партии из 10 изделий 3 бракованных. Наугад взяли 5 изде-

лий. Событие А — два из пяти взятых — бракованные.

8) Событие А — хотя бы один из трех проверяемых приборов —

брак, событие В — все приборы –доброкачественные. Что озна-

чают события А + В, АВ?

9) Событие А — выбранное наугад число делится на 5, собы-

тие В — данное число оканчивается нулем. Что означают события

А\В, А

10) Два шахматиста играют одну партию. Событие А — выиг-

рывает первый игрок, событие В — выигрывает второй. Какое

событие нужно добавить к указанной совокупности, чтобы полу-

чить полную группу событий?

Задачи к разд. 34.3

Задача 1. В урне 4 белых и 6 черных шаров. Выбрали наугад один

шар. Найти вероятность того, что этот шар будет белым.

Решение: Пространство элементарных событий Ω содержит

10 равновозможных элементарных событий ω

(выбор одного

шара). Случайное событие А — выбор белого шара, т.е. А содержит

4 элементарных события. Вероятность Р(А) события А определя-

ется по формуле определения вероятности: Р(А) = m/n, где m = 4,

а n = 10. Имеем Р(А) = 4/10 = 2/5.

313

Задача 2. Набирая номер телефона, абонент забыл последние

две цифры и, помня, что они различны, набрал их наугад. Найти

вероятность того, что набраны нужные цифры.

Решение: Пространство элементарных событий Ω содержит эле-

ментарные события ω

= (n

, m

), n

, m

∈ 0, 1, 2, …, 9 , n

≠ m

Их число N есть число размещений из 10 по 2, т.е. по формуле ОК,

разд. 34.1, N = 10!/8! = 90. Событие А содержит только одно эле-

ментарное событие; таким образом, искомая вероятность Р(А) =

= 1/90.

Задача 3. В партии из 10 деталей семь деталей — стандартных.

Найти вероятность того, что среди взятых наугад пяти деталей три

детали стандартные.

Решение: Пространство элементарных событий Ω содержит эле-

ментарные события ω

(выбор пяти деталей из десяти), число ко-

торых N определяется как число сочетаний из 10 по 5, т.е. N =

= С

252. Случайное событие А включает такие ω

, для

которых из этих пяти деталей три — стандартные. Их число M есть

произведение числа способов, которыми можно из имеющихся

7 деталей выбрать 3 (число сочетаний из 7 по 3, С

), на число спо-

собов, которыми можно выбрать оставшиеся 5 - 3 = 2 детали и

10 - 7 = 3 имеющиеся нестандартные детали (число сочетаний из

3 по 2, С

). Следовательно, M = C

⋅ C

105. Таким

образом, находим вероятность Р(А) = M/N = 105/252 = 5/12.

В общем виде задача формулируется следующим образом.

В партии из n изделий k стандартных. Определить вероятность Р

того, что среди выбранных наудачу m изделий (m < n) l изделий

окажутся стандартными. Формула для определения вероятности P

события А: «l изделий из выбранных m стандарные» запишется в

виде

() .=

В случае l = m формула упрощается:

() .=

Задача 4. Слово МАТЕМАТИКА составлено из карточек, на

которых написано по одной букве. Карточки перемешивают и

берут безвозвратно по одной. Найти вероятность того, что буквы

будут взяты в нужном порядке.

314

Решение: Пространство элементарных событий Ω содержит эле-

ментарные события {ω

}, где {ω

} — некоторая последовательность

букв. Число элементарных событий N определяется числом пере-

становок из 10 букв, так как в данном слове 10 букв. Тогда по фор-

муле ОК, разд. 34.1, N = 10! Событие А состоит в получении слова

МАТЕМАТИКА. Так как буква «М» встречается в слове 2 раза,

буква «А» — три раза, буква «Т» — 2 раза, то возможны перестанов-

ки, при которых слово не меняется. Число этих перестановок

M = 2!3!2! и составляет число элементарных событий, входящих в

событие А. Окончательно получим вероятность Р(А) = M/N =

232

!!!

1/151 200.

Задача 5. Два игрока по очереди бросают игральную кость, каж-

дый по одному разу. Выигрывает тот, кто получит большее число

очков. Найти вероятность выигрыша первого игрока.

Решение: Пространство элементарных событий Ω содержит эле-

ментарные события ω

= (n

, m

), n

, m

∈ 0, 1, 2, …, 6 . Его мож-

но изобразить в виде матрицы

Ω=

(, )(,) (, ) ... (, )

(,)(,) (, ) ... (, )

... ... ... .

11 12 13 16

21 22 23 26

... ...

(,)(,) (, ) ... (,)

61 62 63 66













Очевидно, что число элементарных событий N равно N = 36.

Событие А включает те, для которых n

> m

, их число М легко

можно определить из матрицы: М = 15. Отсюда вероятность

Р(А) = М/N = 15/36 = 5/12.

Задача 6. На отрезке АВ длиной 20 см помещен меньший отре-

зок CD длиной 10 см. Найти вероятность того, что наугад брошен-

ная на отрезок АВ точка попадет внутрь отрезка CD.

Решение: Необходимо использовать геометрическое определе-

ние вероятности, причем в данном случае Р(А) = L

= 10/20 = 1/ 2.

Задачи для самостоятельного решения

11) Куб, все грани которого окрашены, распилен на 1000 ма-

леньких кубиков одинакового размера, которые затем перемеша-

315

ны. Найти вероятность того, что наугад взятый кубик будет иметь

одну окрашенную грань.

12) Брошены одновременно две монеты. Какова вероятность

появления герба («орла») на одной из них?

13) Из карточек составлено слово ПОБЕДА. Буквы перемеша-

ны. Найти вероятность того, что две наугад выбранные буквы —

гласные.

14) Из колоды карт (52 штуки) наугад выбирают три карты.

Какова вероятность того, что это будут тройка, семерка, туз?

15) Кодовый замок состоит из пяти барабанов. Каждый барабан

имеет 6 граней с цифрами от 1 до 6. Замок открывается, если на-

брано определенное число. Найти вероятность того, что при слу-

чайном наборе пяти цифр замок откроется.

16) Девять книг расставлены наугад на полке. Найти вероят-

ность того, что две определенные книги окажутся рядом.

17) Брошены три игральные кости. Найти вероятность того, что

сумма выпавших на них цифр будет равна 6.

18) Круглая мишень быстро вращается с постоянной скоро-

стью. Пятая часть площади мишени окрашена в черный цвет, ос-

тальная часть — в белый. По мишени производится выстрел, при-

чем попадание — достоверное событие. Найти вероятность того,

что пуля попадет в окрашенную в черный цвет часть мишени.

19) На плоскости начерчены концентрические окружности ра-

диусами 5 и 10 см. Найти вероятность того, что брошенная наугад

в большой круг точка попадет в кольцо между большей и меньшей

окружностями.

Задачи к разд. 34.4

Задача 1. В денежно-вещевой лотерее на серию 1000 билетов

приходится 120 денежных и 80 вещевых выигрышей. Найти веро-

ятность какого-либо выигрыша на один лотерейный билет.

Решение: Пространство элементарных событий Ω содержит эле-

ментарные события ω

, состоящие в приобретении i-го билета,

i ∈

11000,

. Случайное событие А состоит в денежном выигрыше на

купленный билет, случайное событие В — в вещевом выигрыше,

случайное событие С — в любом выигрыше. Тогда С = А + В

(АВ = ∅, т.е. А и В — несовместные события). По теореме сложе-

ния вероятностей Р(С) = Р(А + В) = Р(А) + Р(В). Так как Р(А) =

316

= 120/1000 = 0,12, Р(В) = 80/1000 = 0,08, то Р(С ) = 0,12 +

+ 0,08 = 0,2.

Задача 2. Для двух химических реакторов вероятности беспере-

бойной работы на протяжении одного часа р

= 0,75 и р

= 0,8.

Определить вероятность того, что:

а) оба реактора выйдут из строя в течение часа;

б) оба реактора будут работать бесперебойно в течение часа,

в течение трех часов;

в) будет работать бесперебойно в течение часа хотя бы один

реактор;

г) будет работать бесперебойно в течение часа только один ре-

актор.

Решение: Пространство элементарных событий не рассматрива-

ем, так как заданы вероятности событий.

а) Введем случайные события: А

— бесперебойная работа 1-го

реактора в течение часа, А

— бесперебойная работа 2-го реактора

в течение часа,

— события, противоположные событиям А

и А

, соответствующие выходу реакторов из строя в течение часа,

— оба реактора вышли из строя в течение часа.

Так как Р(А

) = р

= 0,75 и Р(А

) = р

= 0,8, имеем (см. ОК,

разд. 34.4) Р(

) = 1 - Р(А

) = 1 - 0,75 = 0,25, Р(

) = 1 - 0,8 =

= 0,2. События

— независимые, при этом

. Тогда по

теореме об умножении вероятностей Р(

) = Р(

) ×

× Р(

) = 0,25 ⋅ 0,2 = 0,05.

б) Пусть случайное событие С — бесперебойная работа обоих

реакторов в течение часа, D — бесперебойная работа обоих реак-

торов в течение трех часов. Тогда С = АВ, D = ССС и имеем Р(С) =

= Р(А)Р(В) = 0,8 ⋅ 0,75 = 0,6; Р(D) = (Р(С))

= (0,6)

= 0,216.

в) Событие В — работает хотя бы один реактор — противопо-

ложно событию

, поэтому Р(В) = 1 - Р(

) = 1 - 0,05 = 0,95

(вероятность Р(

) найдена в а)). Вероятность события С может

быть найдена и другим образом, если учесть, что С = А ∪ В, и то-

гда Р(С) = Р(А) + Р(В) - Р(АВ) = 0,75 + 0,8 - 0,6 = 0,95.

г) Событие Е — бесперебойная работа только одного реактора

в течение часа — записывается в виде Е = А

В, тогда

Р(Е) = Р(А

) + Р(

В) = Р(А)Р(

) + Р(

)Р(В) =

= 0,8 ⋅ 0,25 + 0,2 ⋅ 0,75 = 0,35.

317

Задача 3. Вероятность попадания в цель при одном выстреле

р = 0,2. Какова вероятность поразить цель, если 2% взрывателей

дают отказы?

Решение: Пусть случайное событие А — попадание в цель при

сделанном выстреле, событие В — взрыватель не дал отказа, собы-

тие С — поражение цели. Тогда С = АВ, условная вероятность

Р(А/В) = р = 0,2, Р(

) = 0,02, Р(В) = 1 - Р(

) = 0,98. Следова-

тельно, Р(С) = Р(АВ) = Р(А)Р(В) = 0,98 ⋅ 0,2 = 0,196.

Задача 4. В пирамиде 19 винтовок, из них 3 с оптическим прице-

лом. Стрелок, стреляя из винтовки с оптическим прицелом, может

поразить мишень с вероятностью 0,81, без оптического прицела —

с вероятностью 0,46. Найти вероятность того, что стрелок поразит

мишень, стреляя из винтовки, взятой наугад из пирамиды.

Решение: Введем случайные события: Н

— взята винтовка с

оптическим прицелом, Н

— взята винтовка без оптического при-

цела, А — стрелок поразит мишень. События Н

и Н

— несовмест-

ные, Н

+ Н

= Ω , т.е. Н

и Н

образуют полную группу событий,

причем Р(Н

) = 3/19, а Р(Н

) = 16/19. Из условия задачи известны

условные вероятности Р(А/Н

) = 0,81, Р(Н

) = 0,46. Воспользу-

емся формулой полной вероятности А ∈ Ω: Р(А) = Р(Н

) ×

× Р(А/Н

) + Р(Н

) ⋅ Р(А/Н

) = (3/19) ⋅ 0,81 + (16/19) ⋅ 0,46 =

= 0,515.

Задачи для самостоятельного решения

20) При стрельбе по мишени вероятность сделать выстрел на

оценку «отлично» р

= 0,3, на «хорошо» — р

= 0,4. Найти веро-

ятность выстрела на оценку не ниже «хорошо».

21) Вероятность изготовить детали 1-го сорта на первом станке

= 0,7, на втором станке — р

= 0,8. На первом станке изготов-

лено две детали, на втором — три. Найти вероятность того, что все

они первого сорта.

22) Вероятность попадания в цель из первого орудия р

= 0,8,

из второго — р

= 0,7, из третьего — р

= 0,9. Найти вероятность

того, что при залпе из всех трех орудий: а) хотя бы одно попадет в

цель, б) только одно попадет в цель.

23) Студент знает 20 из 25 вопросов программы. Найти вероят-

ность того, что студент знает предложенные ему экзаменатором два

вопроса.

318

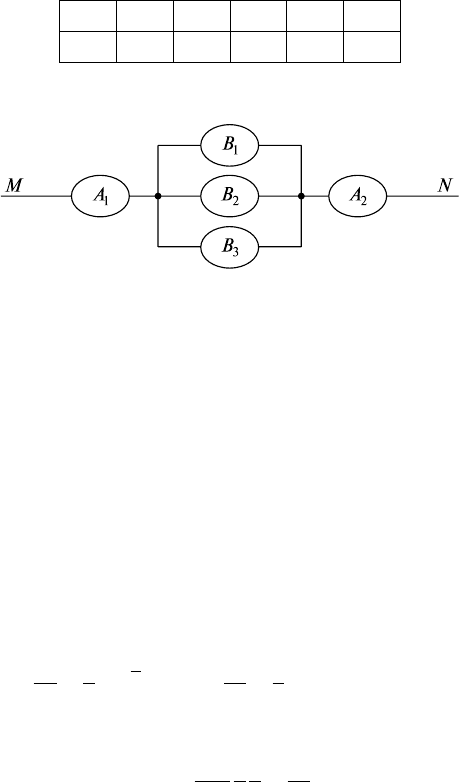
24) Электрическая цепь между точками М и N приведена на

рис. 34.1. Выход из строя различных элементов цепи за время t —

независимые события с известными вероятностями р

0,5 0,5 0,4 0,7 0,9

Определить вероятность разрыва цепи за время t.

Рис. 34.1

25) В цехе при одинаковой производительности станки перво-

го типа производят 94% деталей первого сорта, станки второго

типа — 90%, третьего типа — 85%, причем все произведенные за

смену детали сложены в нерассортированном виде на складе.

Определить вероятность того, что взятая наугад деталь будет пер-

вого сорта, если в цехе 5 станков первого типа, 3 — второго и 3 —

третьего.

Задачи к разд. 34.5

Задача 1. В урне 20 белых шаров и 10 черных. Вынули подряд

4 шара, причем каждый раз вынутый шар возвращали в урну. Ка-

кова вероятность того, что два раза были вынуты белые шары?

Решение: Введем случайное событие А — вынут белый шар, тогда

Р(А) = р =

= ,

Р(

) = q =

= ,

причем событие А должно

появиться при четырех независимых испытаниях два раза. По фор-

муле Бернулли (см. ОК, разд. 34.5) искомая вероятность Р

(2) =

= С

= C

(2/3)

(1/3)

Задача 2. Определить вероятность того, что в семье из пяти де-

тей три девочки. Вероятности рождения мальчика и девочки оди-

наковы.

319

Решение: Введем случайное событие А — рождение девочки,

тогда Р(А) = р = 1/2, Р(

) = q = 1/2. Имеем схему испытаний

Бернулли, где n = 5, m = 3, т.е. искомая вероятность Р

(3) =

= С

(1/2)

Задачи для самостоятельного решения

26) Вероятность изготовления на станке стандартной детали

равна 0,9. Определить вероятность того, что из шести изготовлен-

ных на этом станке деталей четыре детали будут стандартными.

27) Что вероятнее выиграть у равносильного противника (ни-

чейный исход партий исключен): три партии из четырех или пять

партий из восьми?

28) Оптовая база снабжает 10 магазинов, от каждого из которых

может поступить заявка с вероятностью 0,4 независимо от заявок

других магазинов. Найти наивероятнейшее число µ заявок в день

и вероятность получения этого числа заявок.

Указание: Наивероятнейшее значение µ числа m появлений со-

бытия А при n независимых испытаниях, в каждом из которых

вероятность появления события А равна р, вычисляется по форму-

ле µ = [(n + 1)p] — целая часть числа.

35. случайные величины

опорный конспект № 35

35.1. Дискретные и непрерывные СВ. Закон распределения

О: СВ ξ ⇔ ξ = ξ(ω), ω ∈ Ω, ξ ∈ R. Дискретная СВ ⇔

ξ = (x

, x

, ..., x

). Непрерывная СВ ⇔ ξ ∈ (a, b)

О: Ряд распределения СВ — таблица

... x

∑

= 1

P p

... p

О: Функция распределения СВ ξ: F(x) = Р(ξ < x), x ∈ R

О: Плотность распределения непр. СВ ⇔ ϕ(х): F′(x) = ϕ(x).

Fx tt xx() () ,().==

-∞

∞

-∞

∞

∫∫

ϕϕdd1

320

Px xxx

()()

≤≤ =

∫

ξϕd

35.2. Числовые характеристики СВ

О: Математическое ожидание дискретной СВ

ξ = (x

, x

, ..., x

), Р(ξ = х

) = p

⇔

Mxp

()ξ=

∑

Математическое ожидание непр. СВ ξ с плотностью вероятно-

сти ϕ(x) ⇔

Mxxx() ()ξϕ=

-∞

∞

∫

Дисперсия СВ ξ ⇔ D(ξ) = M((ξ - M(ξ))

). Среднее квадрати-

ческое отклонение СВ ξ ⇔ σ(ξ) =

D()ξ

35.3. Примеры распределений дискретных и непрерывных СВ

О: Равномерное распределение дискретной СВ

ξ = (x

, x

, ..., x

) ⇔ Р(ξ = х

) = 1/n,

in= 1,

⇒

⇒= =-













===

∑∑∑

() ,()ξξ

111

О: Биномиальное распределение

СВ ξ = (1, 2, ..., n) ⇔ P(ξ = i) = C

n-i

in= 1,;

p, q определены в разд. 34.5 ⇒ М(ξ) = np, D(ξ) = npq

О: Распределение Пуассона СВ ξ = (1, 2, ..., n) ⇔ P(ξ = i) =

= (λ

/i!)e

-λ

, λ = np; p определено в разд. 34.5 ⇒ M(ξ) = D(ξ) = λ

О: Равномерное распределение непрерывной СВ ξ ∈ [a, b] ⇔

⇔ ϕ(x) = c, c = const, x ∈ [a, b] ⇒ с = 1/(b - a),

M(ξ) = (a + b)/2, D(ξ) = (b - a)

/12

О: Нормальное распределение

СВ ξ ⇔

σπ

() ,

()

х ∈ (-∞, +∞);

m = M(ξ),

σξ= D()

35.4. Многомерные СВ

О: Многомерная СВ ζ ⇔ ζ = ζ(ω) = (ξ

(ω), ξ

(ω), ..., ξ

(ω)),

ζ ∈ R

, ω ∈ Ω

О: Функция распределения вероятностей СВ ζ = (ξ, η) ⇔

⇔ F(x, y) = P(ξ < x, η < y)

Fxytttt

(, )(,) ,=

-∞-∞

∫∫

12 12

ϕ(x, y) — плотность вероятности,