Журбенко Л.Н., Никонова Г.А., Никонова Н.В., Нуриева С.Н., Дегтярева О.М. Математика в примерах и задачах

Подождите немного. Документ загружается.

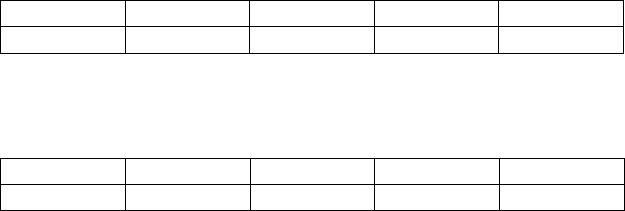
341

23) Дана функция

ϕ()

(),;

ax x

ax xx

≤

<≤

-<≤











212

При каком значении а ϕ(х) является плотностью распределения

случайной величины ξ ∈ (0, 2)? Найти математическое ожидание

М(х).

24) Дискретная случайная величина задана рядом распределе-

ния:

-5 2 3 4

р 0,4 0,3 0,1 p

Найти р

, функцию распределения, среднее квадратическое

отклонение.

25) Выборка задана в виде распределения частот:

4 7 8 12

m 5 2 3 10

Записать статистический ряд, построить полигон, эмпиричес-

кую функцию распределения, математическое ожидание, диспер-

сию.

26) В результате испытания случайная величина ξ приняла сле-

дующие значения: 16, 17, 9, 13, 21, 11, 7, 7, 19, 5, 17, 5, 20, 18, 11, 4,

6, 22, 21, 15, 15, 23, 19, 25, 1. Составить интервальный статистичес-

кий ряд, разбив промежуток (0, 25) на 5 интервалов с одинаковыми

длинами. Построить гистограмму.

27) Пятнадцать студентов группы, выбранных случайным об-

разом, имеют следующие оценки по результатам сессии: 5, 4, 4, 3,

2, 2, 4, 3, 3, 5, 3, 3, 4, 2, 3. Составить статистический ряд, найти

эмпирическое математическое ожидание, моду (наиболее вероят-

ное значение), среднее квадратическое отклонение, построить

полигон.

28) Из нормальной генеральной совокупности с известными

m = 130, σ = 40 извлечена выборка объемом n = 64 и найдено

выборочное математическое ожидание m* = 136,5. Требуется при

уровне значимости 0,01 проверить нулевую гипотезу Н

: m* = m

при конкурирующей: а) m ≠ m*; б) m* > m.

342

(Указание: воспользоваться критерием

mm n

- *

)

29) Установлено, что средний вес таблетки лекарства сильного

действия должен быть равен m = 0,5 мг, причем вес таблеток рас-

пределен нормально, σ = 0,11 мг. При выборочной проверке

121 таблетки из партии лекарств получено выборочное математи-

ческое ожидание m* = 0,53 мг. Требуется при уровне значимости

0,01 проверить нулевую гипотезу Н

: m = m* при конкурирующей

гипотезе Н

: m* > m.

30) Одним и тем же прибором со средним квадратическим от-

клонением случайных ошибок измерения σ = 40 м произведено

пять равноточных измерений расстояния от орудия до цели. Сред-

нее арифметическое результатов измерений m* = 2000 м. Найти

доверительный интервал для оценки истинного расстояния до цели

с надежностью γ = 0,95.

варианты контрольной работы

Вариант 1

1. Бросают одновременно три монеты. Найти вероятность по-

явления герба на двух из них. Ответ: 3/8.

2. В группе 20 лыжников, 4 бегуна, 6 велосипедистов. Вероят-

ность выполнения нормы для лыжника — 0,9, для велосипедиста —

0,8, для бегуна — 0,75. Найти вероятность того, что наудачу вы-

бранный спортсмен выполнит норму. Ответ:

p =⋅ +⋅ +⋅

075,, ,.

p =⋅ +⋅ +⋅

075,, ,.

3. Непрерывная случайная величина ξ имеет следующую функ-

цию распределения:

xx x

()

-≤≤

≥











201

Найти плотность вероятности ϕ(x), математическое ожидание

М(ξ), дисперсию D(ξ). Ответ: М(ξ) = 1/3; D(ξ) = 1/18.

4. По выборке (n = 15) построен статистический ряд случайной

величины:

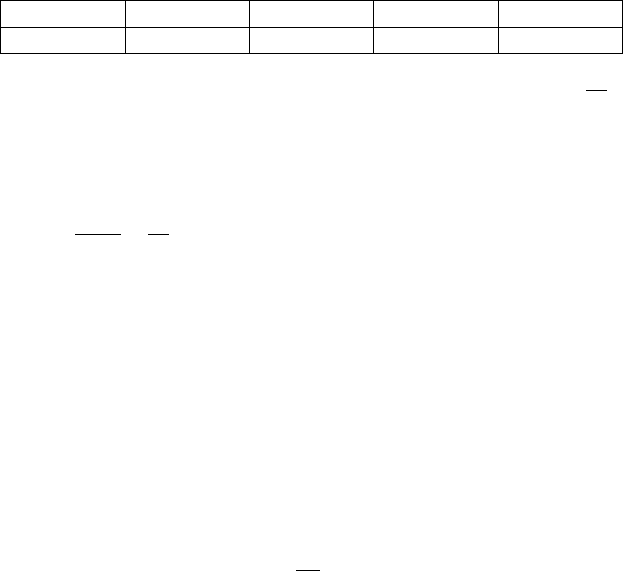
343

2 4 6 8

p* 1/5 2/5 1/15 m/15

Найти m, F*(x), M*(2ξ + 3). Ответ: m = 5; M*(2ξ + 3) = 13

Вариант 2

1. В урне 4 белых и 5 черных шаров. Найти вероятность того,

что среди выбранных наудачу трех шаров будут два белых шара.

Ответ:

= .

2. Вероятность поражения первой мишени для данного стрел-

ка равна 2/3. Если при первом выстреле зафиксировано попада-

ние, то стрелок получает право на выстрел по второй мишени.

Вероятность поражения обеих мишеней при двух выстрелах рав-

на 0,5. Определить вероятность поражения второй мишени.

Ответ: 0,75.

3. Производятся последовательные независимые испытания

пяти приборов на надежность. Каждый следующий прибор испы-

тывается только в том случае, если предыдущий оказался надеж-

ным. Построить ряд распределения случайного числа испытанных

приборов, если вероятность выдержать испытания для каждого

прибора равна 0,9. Найти функцию распределения. Ответ: p

= P(x = i) = 0,1 ⋅ (0,9)

i-1

i = 14,,

= (0,9)

4. По выборке m = 10 построена эмпирическая функция рас-

пределения:

()

,, ;

≤

<≤











02 12

05 23

08 34

Построить статистический ряд. Сколько раз наблюдалось зна-

чение 3? Найти М(3ξ + 5). Ответ: 3 раза; М(3ξ + 5) = 12,5.

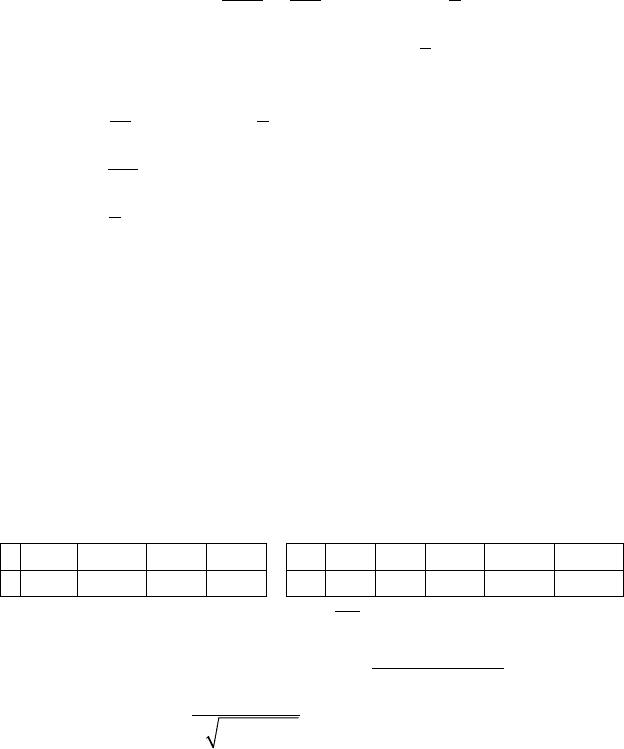
344

ответы к разд. 34, 35, 36

34. Основные понятия теории вероятностей

1) C

⋅ C

; 2) C

⋅ C

; 3) A

; 4) р

= 6!; 5) n = 6, m = 3;

6) n = 16, m = 6; 7) n = C

, m = C

⋅ C

; 8) A + B = Ω, AB = 0;

9) Число оканчивается цифрой 5; 10) Событие С — ничейный

результат; 11)

PA() ;==

384

1000

125

12)

PA() .=

Указание: Ω =

= {(r, r), (r, p), (p, r), (p, p)}; 13)

PA() .=

Указание: m = C

n = C

; 14) P(A) = 0,0029. Указание: m = 4

, n = C

;

15)

PA() ;=

16)

PA() .=

Указание: m = 8 ⋅ 7! ⋅ 2!, n = 9!;

17)

PA() .=

108

Указание: m = 4 + 3 + 2 + 1 = 10, n = 6 ⋅ 6 ⋅ 6;

18)

PA() ;=

19) P(A) = 0,75; 20) P(A) = 0,7; 21) P(A) = 0,25;

22) a) p = 0,994; б) p = 0,092; 23) P(С) = 19/30. Указание: С =

= АВ, А — студент знает первый вопрос, В — студент знает второй

вопрос, Р(А) = 20/25, Р(В/А) = 19/24; 24) Р(С) = 0,81. Указание:

С = А ∪ В, А — выход из строя хотя бы одного элемента, В — вы-

ход из строя всех трех элементов; 25) Р = 0,91. Указание: Восполь-

зуйтесь формулой полной вероятности, если Ω = В

+ В

— детали, выпущенные станком i-го типа; 26) Р

(4) = 0,0984;

27) Три партии из четырех. Указание: Находим Р

(3) и Р

(5) ⇒

⇒ 1/4 > 7/32; 28) µ = 4, Р

(4) = 0,251.

35. Случайные величины

1) 2)

0 1 2 3

0 1 2 3 4

p 0,125 0,375 0,375 0,125 p 0,5 0,25 0,125 0,0625 0,0625

Указание: р

= 0,5 ⋅ (0,5)

i-1

i = 14,;

= 0,5

;

3) а) а = k

/2; б)

kx kx

() ;=-

в) 0,086;

4) а) 1/3; б)

()

x ∈ (-a, a); 5) а) M(ξ) = 0,501,

D(ξ) = 0,077; б) M(ξ) = 1,5, D(ξ) = 0,75; 6) М(ξ) = 4/3; D(ξ) =

= 2/9; 7) М(ξ) = 0; D(ξ) = a

/2; 8) P(ξ = i) = C

(0,6)

(0,4)

5-i

;

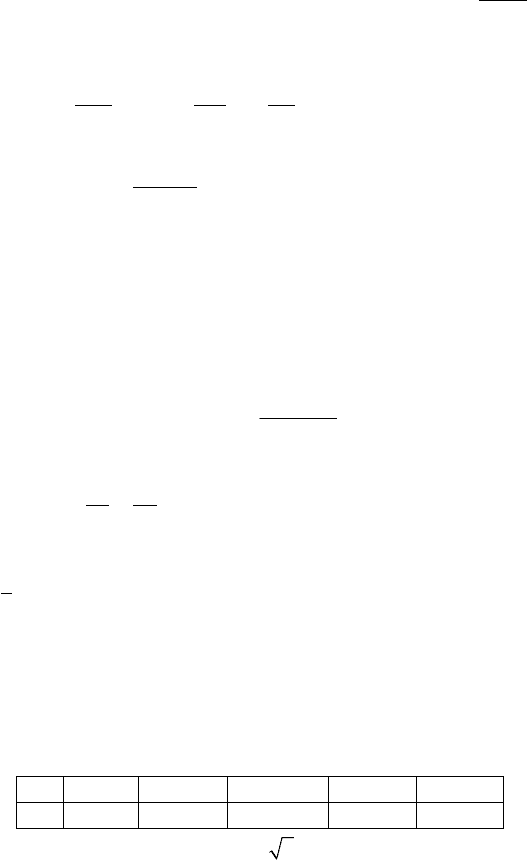
345

М ( ξ ) = 3; D ( ξ ) = 1,2; 9)

P()

,;ξ= ==

017

10) a) P(3 < ξ < 5) = 1/3; б) М(ξ) = 5; D(ξ) = 3;

11) P(|ξ| < 150) = 0,819; 12) р = 0,758; 13) P(ζ ∈ D*) = 1/24;

14) a)

;

б)













;

15) М(ξ) = (0, 0); 16) D(ξ) =

= D(η) = π - 3; R(ξ, η) = 0; 17) ϕ(x, y, z) = abce

-(ax+by+cz)

. Ука-

зание:

ϕ(, ,) .xyz

xyz

∂

∂∂∂

36. Элементы математической статистики

1) б) М* = 201; D* = 1754. Нормальный закон распределения;

2) (94,9 м, 105,1 м); 3) k = 6; χ*

= 7,09. Гипотезу можно принять.

Указание: Последние два интервала объединяются; 4) Принима-

ется Н

; 5) а) 1/6; б) 1/4; 6) 0,844; 7) 6/29; 8) M = 7; D = 4/3;

9) M = 1; D = 16/3; 10) 3,2; 11) 5; 36; 12) 15; 13) 17; 14) 1/17;

15) 0,806; 16) 0,1; 17)

tT t

()

;

18) 15/26; 19) 4/9;

20)

()

≤

-<≤











216

21) 2/9; 22) 10; 23) a = 1, M(ξ) =

;

24) p

= 0,2, σ(ξ) = 3,9; 25) M*(ξ) = 8,9; D*(ξ) = 18,475;

*()

,, ;

≤

<≤









0254 7

0357 8

05 812

112





;

26)

(0,5) [5,10) [10,15) [15,20) [20,25)

p* 0,12 0,2 0,16 0,32 0,2

27) M*(ξ) = 10/3; σ*(ξ) = 2

/3; мода m* = 3; 28) а) u

набл

= 1,3; u

кр

= 2,57; принимается Н

; б) u

кр

= 2,33; принимается Н

29) u

набл

= 3; принимается Н

; 30) 1964,94; 2035,06.

346

расчетное задание

Здесь n — номер студента по списку, αβγδ — цифры номера

группы; а - 1 = ](n + γ + δ)/5[, b - 1 = ](n + β)/4[, k - 1 =

= ](n + α)/3[, d = ]n/2[.

1. В партии из 12 + а + b деталей 6 + b + k стандартных. Най-

ти вероятность того, что среди отобранных наудачу 5 + b + d де-

талей 4 + d стандартные.

2. Бросают одновременно 2 + d игральных костей. Найти ве-

роятность того, что сумма выпавших цифр меньше 3 + k + b +

+ (-1)

n+1

3. Cлово содержит 2 + a + b + k различных букв. Буквы пе-

ремешаны. Какова вероятность, что, беря случайным образом по

одной букве и складывая их последовательно, мы получим задан-

ное слово из (2 + а) букв.

4. Имеется b + 1 различных станков. Вероятность отказа каж-

дого в течение одного часа 0, b. Какова вероятность, что в течение

а + 1 часа: а) ни одному из станков не потребуется ремонт; б) хотя

бы одному станку не потребуется ремонт; в) только одному станку

потребуется ремонт?

5. На фабрике болты изготавливают 3 + d станков, причем

первая машина изготавливает b ⋅ 10% всех болтов, а остальные —

равные количества болтов. Брак продукции составляет для первой

машины а%, а для остальных k%. Найти вероятность того, что

оказавшийся бракованным болт изготовлен на первой машине.

6. По цели производится 2 + k независимых выстрелов. Веро-

ятность попадания при каждом выстреле равна (а + 2)/10. Соста-

вить ряд распределения случайного числа попаданий. Найти F(x),

M(ξ), D(ξ), σ(ξ).

7. Производят последовательные независимые испытания

2 + b приборов на надежность. Каждый следующий прибор испы-

тывают только в том случае, если предыдущий оказался надежным.

Построить ряд распределения числа испытанных приборов, если

вероятность выдержать испытание для каждого равна (k + 4)/10.

Найти F(x), M(ξ), D(ξ), σ(ξ).

8. Плотность распределения случайной величины ξ

ϕ()

,, .

axabk

xaxabk

<<++

<>++











Найти с, F(x), M(ξ), D(ξ).

9. Функция распределения случайной величины ξ

abx

()

-≥











10e

Найти M(ξ), D(ξ), P(0 < ξ < b).

10. Плотность распределения случайной величины ξ

() .

()

Найти M(aξ + b + k), D(aξ + b + k).

11. Выборка задана в виде ряда распределения частот:

k + 1 k + 3 k + 5 k + 7

m b + 2 a b + 1 a + 3

Записать статистический ряд, построить полигон, найти эмпи-

рическую функцию распределения, математическое ожидание,

дисперсию, среднее квадратическое отклонение.

12. По данным измерений двух переменных построена таб-

лица:

k + 1 b + 1 a + 2 k + 3 a + 3

k + 2 b a + 4 k + 5 a + 2

Найти выборочный коэффициент корелляции и прямые регрес-

сии.

348

Глава 13

дискретнаЯ математика

37. лоГические исчислениЯ

опорный конспект № 41

37.1. Логика высказываний

Высказывание а = {0, 1} — логическая переменная

Логические операции:

1. Коньюнкция:

cab

=∧=







111

,,,

если

в остальных случаях

2. Дизъюнкция:

cab

=∨=







000

,,,

если

в остальных случаях

3. Импликация:

ca b

=⇒=







010

,,,

если

в остальных случаях

4. Отрицание:







если

5. Эквивалентность:

ca b

ab ab

=⇔=

== ==







110

если или

в остальных случаях

Формула q = F (p

, p

, ..., p

) — булева функция n перемен-

ных

37.2. Равносильные формулы логики высказываний

aa= .

2. а ∧ b = b ∧ a, a ∨ b = b ∨ a.

3. (a ∧ b) ∧ c = a ∧ (b ∧ c), (a ∨ b) ∨ c = a ∨ (b ∨ c).

4. a ∧ (b ∨ c) = (a ∧ b) ∨ (a ∧ c); a ∨ (b ∧ c) =

= (a ∨ b) ∧ (a ∨ c).

abababab∧=∨∨=∧,.

6. a ∧ a = a, a ∨ a = a.

7. a ∧ 1 = a, a ∨ 1 = 1.

349

8. a ∧ 0 = 0, a ∨ 0 = a.

9. a ∧

= 0, a ∨

= 1.

10. a ⇒ b =

∨ b.

11. a ⇒ b =

⇒

12. a ⇔ b = (a ⇒ b) ∧ (b ⇒ a) = (a ∧ b) ∨ (

∧

)

Т: Любая булева функция n переменных представима в виде

дизъюнктивной нормальной формы (дизъюнкции конъюнкций из

) 

37.3. Элементы логики предикатов

О: Предикат P(x

, x

, ..., x

) — функция: x

∈ M,

in= 1,,

P = {0, 1}

P(x

, x

, ..., x

) — тождественно истинный на М, если при лю-

бых x

= а

∈ M,

in= 1,,

P(a

, a

, ..., a

) = 1

Кроме логических операций вводятся:

а) квантор общности ∀х:

∀xP(x) ⇔ для всех х из М значение P(x) = 1;

б) квантор существования ∃х:

∃хP(x) ⇔ существует х из М, что Р(х) = 1;

∀x

P(x

, x

, ..., x

) = Q(x

, ..., x

i-1

, x

i+1

, ..., x

)

37.4. Понятие о формальных системах, языках и грамматиках

О: Алфавит V = {a

, a

, ..., a

}, a

— символы (буквы, цифры,

знаки операций)

Слова (цепочки) α, ξ — последовательности k символов

Формальная грамматика G = <V, W, J, R>, где V — алфавит

основных символов; W — алфавит вспомогательных символов,

V ∩ W = ∅; J — начальный символ (аксиома); R — конечное мно-

жество правил вывода ξ

η; ξ, η — цепочки в алфавите V ∪ W

Язык L(G) — множество всех цепочек в V, выводимых из J

Задачи к разд. 37

Задача 1. Записать таблицу истинности для формулы q =

= p

∨

⇒ p

Решение: Запишем таблицу истинности для q* = p

∨

, ис-

пользуя ОК, разд. 37.1:

q* = p

∨

1 1 0 1

1 0 1 1

350

q* = p

∨

0 1 0 0

0 0 1 1

Тогда, используя определение импликации, имеем для q следу-

ющую таблицу истинности:

1 1 1 1

1 0 1 1

1 1 0 0

1 0 0 0

0 1 1 1

0 0 1 1

0 1 0 1

0 0 0 0

Задача 2. Группа из нескольких человек планирует воскресный

поход за город. Решено, что два организатора похода придут на

место сбора в любом случае, но поход состоится лишь при одном

из условий:

1) если не найдется палатки, то не должно быть дождя;

2) если пойдет дождь, то должна быть палатка и компания боль-

ше пяти человек.

Требуется записать высказывание q — «поход состоится» в виде

нормальной дизъюнктивной формы, упростить ее и сформулиро-

вать условия 1), 2) более кратко.

Решение: Пусть р

— высказывание «пойдет дождь», р

— «най-

дется палатка», p

— «собралось больше пяти человек»; запишем

q = f(p

, p

) по заданным условиям в виде таблицы истинно-

сти:

1 1 1 1

1 0 1 0

1 1 0 0

1 0 0 0

0 1 1 1

0 0 1 1