Жарков В.Н. Внутреннее строение Земли и планет

Подождите немного. Документ загружается.

функции (),„ которая является мерой рассеяния меха

нической энергии в различных слоях планеты. В элект

ротехнике Q определяет добротность электрических кон

туров. В механике диссипативную функцию Q[t можно

назвать механической добротностью системы; она равна

отношению энергии, накопленной в системе, к энергии,

рассеянной в течение цикла [см. формулу (4) в § 1.21.

Q, определяют или по ширине спектральной липни, или

по спаданию со временем амплитуды собственных коле

баний. Величину можно также рассматривать как

«меру идеальности» упругости среды. Чем больше зна

чение Q)t, тем меньшая часть механической энергии при

колебаниях рассеивается и переходит в тепло, тем ближе

среда к идеально упругой. Поясним теперь, почему у

стоит индекс р. В § 1.2 при рассмотрении затухания объ

емных Р- и iS’-волп мы у соответствующих Q проставили

индексы Р и S [см. формулу (3)], показывая тем самым,

к каким волнам относится рассматриваемое Q.

При собственных колебаниях или при распростране

нии воли в недрах Земли возникают напряжения. Любое

напряжение (пли напряженное состояние) можно разло

жить на две части: напряжение чистого сдвига и напря

жение всестороннего сжатия (или растяжения). Часть

напряжения, представляющая напряжение чистою сдви

га, пропорциональна модулю сдвига р,, а другая часть

напряжения — напряжение всестороннего сжатия — про

порциональна модулю сжатия К. Процессы всесторонне

го сжатия являются практически идеально упругими по

с равнению со сдвиговыми процессами. Затухание собст

венных колебаний, и, видимо, всех остальных механиче

ских колебании земных недр происходит из-за отклоне

ния материала от идеальной упругости по отношению

к сдвиговым напряжениям. Образно это передают слова

ми, говоря, что рассеяние механической энергии связано

с релаксацией модуля сдвига р. Количественной мерой

этого рассеяния является величина [см. формулу (4)J.

Из-за того, что неупругость среды при процессах всесто

роннего сжатия (расширения) много меньше, чем при

сдвиговых процессах, говорят, что модуль сжатия К не

релаксирует, и соответствующую количественную меру

«объемной» добротности QK полагают равной бесконеч

ности, Q,; = ОО.

Такттм образом, задача заключается в подборе такого

распределения <?(,(/) с глубиной, чтобы получить согла

сие рассчитанных значений мер затухания крутильных

/Л, ,i и сфероидальных jQa, п топов с паблюдаемыми зна-

■шшшмн этих величин. При этом амплитудные коэффи-

|'мгы затухания собственных колебаний ,«т, » п ^cts, п свя-

■| ны с jQr, п и iQs,n простыми формулами

За Т,п — ТГ7)

Т,п

.ттухаттие амплитуды

S,n

2f i S,n

(40)

Если обратиться к рис. 20, па котором показаны рас

пределения смещений с глубиной, то легко понять, поче

му наблюдения затухания различных гармоник спектра

гобствеииых колебаний позволяют найти распределение

<.\М) с глубиной. Действительно, смещения в разных то-

нпх погружены в недра Земли на различные глубины,

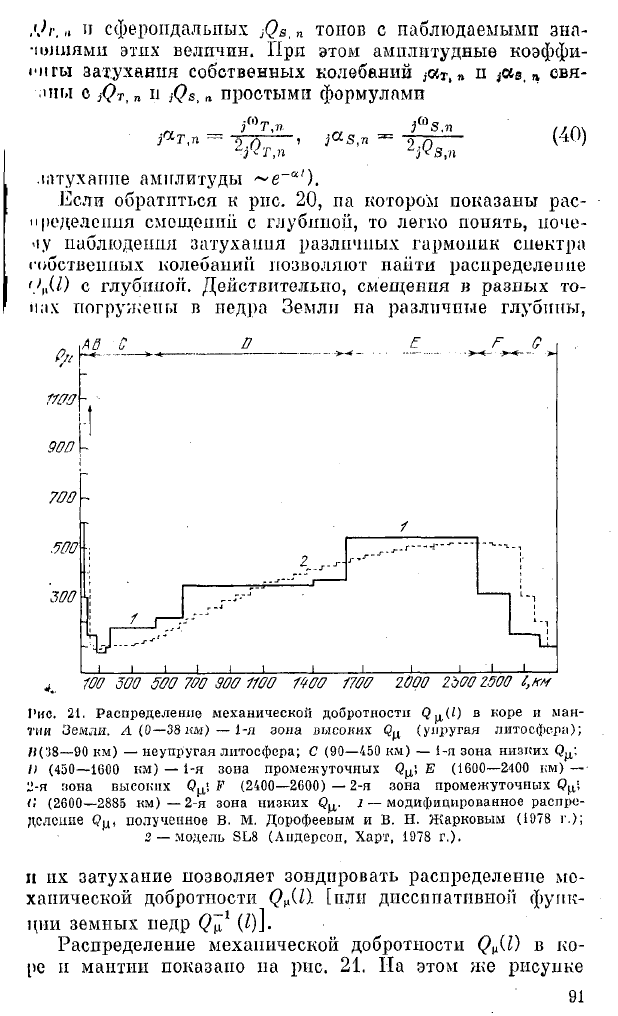
Рио. 21. Распределение механической добротности <3^(0 в коре и ман

тии Земли. А (0— 38 км) — 1-я зона высоких Q^ (упругая литосфера);

/*(’J8—90 нм) — неупругая литосфера; С (90—450 км) — i -я зона низких Q.j'.

II (450—1600 км) — 1-я зона промежуточных Е (1600—2400 км) —

Ц-я зона высоких Q^', F (2400—2600) — 2-я зона промежуточных

I; (2600—2885 км) — 2-я зона низких £?ц. 1 — модифицированное распре

деление полученное В. М. Дорофеевым и В. Н. Жарковым (1978 г.);

2 — модель SL8 (А ндерсон, Харт, 1978 г.).

н их затухание позволяет зондировать распределение ме

ханической добротности [пли диссипативной функ

ции земных недр Q^1 (Z)].

Распределение механической добротности в ко

ре и мантии показано на рис. 21. На этом же рисунке

дано разделение коры и мантии иа различные зоны п<>

Qц. Несмотря на то, что распределение в недрах

Земли еще недостаточно точно определено, тем не менее

уже сейчас можно указать ряд особенностей строения ко-,

ры ы маитии по Наружный жесткий слой Земли (ее

литосфера) разделяется на три зоны: повышенной доб

ротности (0—19 км), Q».~ 600; средней добротности (19—

38 км), (?„ ~ 300, п пониженной добротности (38—90 км),

Q, ~ 150. Далее следует 1-я зона низких QIL в мантии Зем

ли (Андерсон, Аршамбо, 1964 г.). Вторая зона низких

расположена у подошвы мантии (В. Н. Жарком,

Л. II. и В. М. Дорофеевы, В. М. Любимов, 1974 г.). Дне

зоны низких Qn в мантии Земли разделены зоной высо

ких и зоной промежуточных Qn.

Найти распределение Q в земном ядре пока не уда

ется. Можно только сказать, что для жидкого внешнего

ядра Q заметно больше, чем для маитип (Q > 1000). Для

твердого внутреннего ядра Земли (глубины ~ 5100—

6371 км) ~ 100 н- 300.

Остановимся теперь кратко на физической интерпре

тации неупругости твердых зон земных недр. Этот воп

рос все еще остается весьма неопределенным. Видимо,

как нулевое приближение; можно предположить, что не-

упругость в зонах пониженных Qtl и в зонах повышен

ных Qlt обусловлена различными физическими механиз

мами.

Конкретный физический механизм диссипации меха

нических колебаний в земных недрах еще недостаточно

ясен. Можно только указать следующие четыре общие

причины, приводящие к понижению (?ц:1) близость тем

пературы к температуре плавления; действительно, при

относительно высокой температуре кривая зависимости

внутреннего треиия от температуры для большинства ма

териалов непрерывно растет с ростом температуры, до

стигая довольно большой величины; это явление извест

но под названием высокотемпературного фона; 2) нали

чие в веществе заметного количества инородных приме

сей; например, в силикатном веществе низов мантии

(глубины 2600—2900 км) могут иметься космические

«шлаки» типа летучих Н20, С02 и др., которые туда по

пали как выплавки при образовании и эволюции земно

го ядра; 3) частичное плавление, причиной которого так

же может быть наличие указанных выше летучих ве

ществ; 4) релаксация напряжений (скольжение) по гра

ницам зерен в ноликристаллической мантии Земли при

пысоких температурах. Естественно, что все эти причи

ни могут действовать одновременно, но не исключено

" иаличие других факторов, которые сейчас трудно

капать.

Интересной гипотезой является предположение, что

■ >е граничные области мантии Земли представляют со-

ui резервуары космохимических шлаков, которые в

фипципе являются потенциальными источниками текто-

| и ческпх движений.

Учитывая корреляцию низких значений Q» с высоки-

■hi температурами п, в свою очередь, корреляции высо

ких температур с низкими вязкостями, можно иреднола-

i.iTb иаличие в мантии Земли двух астеносферных («рнз-

шгченных») слоев. Первый астеносферпый слой располо

жен на глубинах 70—270 км в верхней мантии в зоне

пониженных скоростей. Второй слой находится у подош-

HI.I мантин, и некоторые сведения о нем стали известны

lo.'ibKO в самое иоследиее время.

Мы знаем, что температура в наружных слоях Земли

■об этом пойдет речь ниже) быстро растет, приближаясь

температуре плавления в зоне пониженных скоростей.

Следовательно, наличие минимума Qlt па глубинах 50—

'•ПО км служит еще одним указанием на близость темпе

ратур в этой зоне планеты к температурам нлавленпя.

Пон рос о температурах в глубинных недрах Земли, у по

дошвы мантии, недостаточно определен. Низкие значения

в этой области, видимо, указывают на то, что эти тем

пературы достаточно высокие.

В гл. 8 при рассмотрении конвекции и механизмов

тектоники плит (§ 8.4.5) будет выяснено, что в конвек-

I и иной мантни должны существовать тонкие перегретые

;оны (АI ~ 150—300 км) — тепловые пограислои. Один

из таких перегретых слоев расположен у подошвы ман-

II1U на границе с ядром. Тем самым зона низких у

чидошвы мантии получила ясное физическое обоснова

ние (В. И. Жарков, 1981 г.). Можно сделать общий вы-

иод, что зоны низких Q,i в мантни соответствуют тепло-

■I ы м иогранслоям. Как будет подробно разъяснено в

8.4.5, в мантин должен также существовать тепловой

ногранслой на глубинах ~ 700—900 км и, следовательно,

н этой же области должна находиться третья зона низ

ких Qn (эта зона еще недостаточно исследована и поэто

му не показана на рис. 21). Более подробно эта новая

интерпретация зон низких <?„ в мантин разъясняется

п § 8.4.5.

Перечисленные выше четыре общие причины, приво

дящие к понижению в первую очередь относятся к

зонам низких Еще более неопределенным является во

прос о физических механизмах поглощения в зонах по

вышенной добротности в мантии Земли. Этот вопрос сло

жен еще и потому, что затухание в земных недрах в ос

новном определяется зонами низких (),, и соответственно

распределение Q^il) в зонах повышенной добротности

определено весьма ненадежно. Тем не менее в последнее 1

время была высказана гипотеза, согласно которой в зо

нах повышенной добротности может оказаться существен

ным механизм температурной релаксации в поликристал

лах. При прохождении упругой волны в зернах поликри-1

сталла возникают небольшие градиенты температуры,

выравнивание которых и.приводит к рассеянию энергии.

Интересной особенностью этого механизма является то,

что одинаково важны как процессы рассеяния энергии

при сдвиговых деформациях (Qц конечно), так и процес

сы рассеяния энергии при объемных деформациях (QK

конечно), причем QK < Q Эта гипотеза в пастоящее вре

мя находится в стадии проверки.

3.3. Динамический модуль сдвига земных недр

Повышение точности и детальности геофизических

данных, оценка диссипативных свойств земных недр, о

которой мы только что говорили, подготовили почву для

принципиально новой постановки задачи о сейсмологи

ческой модели Земли. В § 1.2 при рассмотрении затуха

ния объемных сейсмических волн отмечалось, что как

лабораторный эксперимент, так и геофизический опыт по

казывают независимость от частоты (в первом прибли

жении) величины для горных пород и распределения

Q»(l) в недрах Земли. В то же время до самого послед

него момента считалось, что сейсмологическая модель

Земли (или, как часто говорят, «модель Земли») также

пе зависит от частоты. В последнюю фразу вкладывается

утверждение, что распределение модулей упругости цШ,

К{1) и плотности p(Z) одно и то же, впе зависимости от

того, рассчитываем ли мы времена пробега объемных

сейсмических воли (периоды 0,1 -f- 10 с), дисперсионные

кривые поверхностных воли (периоды 10 с — 3 мин.), ча

стоты собственных колебаний Земли (периоды 3 — 55 мин.)

нлп числа Лява для приливов (периоды от полусуток до

полутора лет).

Переход от упругих моделей Земли к неупругим как

ii.ci и показал, что предположение о независимости мо

ими! Земли от частоты является устаревшим и неверным.

Колее того, неучет этого обстоятельства в значительной

■ре обесценивает многочисленные построения моделей

■ !|‘мли, выполненные в последнее десятилетие. Скажем

азу же, что распределение плотности в недрах Земли

■ I) не зависит от частоты; из-за того, что модуль сжатия

к1 релаксирует (при процессах всестороннего сжатия не

происходит диссипации энергии механических колебаний

|' тепло), распределение KU) также пе зависит от часто-

| ы. А вот из-за того, что диссипация механических коле

баний определяется сдвиговыми процессами (модуль

сдвига р релаксирует), распределение модуля.сдвига в

недрах Земли pU) зависит от частоты, т. е. более пра

вильно следует писать p(Z, ш).

Для разъяснения этого вопроса рассмотрим простей

шее реологическое тело— тело Максвелла.

Реология — это наука о механическом поведении не

идеально упругих тел. Соответственно реологические те-

-•1« — это механические модели пеидеально упругих тел.

Простейшая гуковская модель упругого твердого тела, в

которой напряжения линейно зависят от деформаций,

а коэффициенты пропорциональности.— модули упруго

сти, не является реологической моделью. Эта модель не

обладает пеупругостыо. Возбужденные в гуковском теле

механические колебания продолжались бы неограничен

но долго из-за отсутствия затухания. Можно сказать, что

гуковская модель твердого тела — это идеальная, пре

дельная реологическая модель без затухания. Второй

идеальной моделью является модель идеальной жидкости,

вязкость которой равна пулю. Механические колебания

в такой жидкости также пе затухают. Таким образом, до

самого последнего времени, по существу, рассматрива

лась предельная идеальная модель Земли, кора, мантия

и внутреннее ядро которой «читались гуковским твер

дым телом, а внешнее ядро — идеальной жидкостью.

Простейшей реологической моделью является ньюто

новская вязкая жидкость. Энергия механических колеба

ний в ньютоновской жидкости будет дисспппровать в

тепло из-за вязкого трения. Вообще говоря, вязкая жид

кость — это предельный случай реологического тела Мак

свелла для низких частот (пли, что-то же самое, для

больших периодов). Чисто по-житейски мы всегда легко

отличаем жидкость от твердого тела. Но если поставить

вопрос научно, то это потребует специального определе

ния. Действительно, можно определить жидкость как та

кое состояние вещества, когда тело принимает форму за

ключающего его сосуда. Можно и так сказать, что н

жидкости не существуют поперечные волны, так как

модуль сдвига жидкости равен нулю и она не работает

на сдвиг. Следовательно, жидкость характеризуется толь

ко одним упругим модулем — модулем сжатия К. В нем

могут распространяться только продольные волны Р со

скоростью vP = ~IK/p.

Однако легко видеть, что мы все время ведем речь

о жидкости с малой вязкостью г|. Рассмотрим набор жид

костей со все возрастающими вязкостями. Тогда окажет

ся, что жидкости с достаточно большими вязкостями не

будут принимать форму заключающего их сосуда за обо

зримое время и, кроме того, в таких жидкостях могут

распространяться как продольные, так и поперечные

волны, если только периоды этих волн достаточно корот

кие. Таким образом, совершенно ясно, что требуется чет

ко определить условия, в которых вязкая жидкость про

являет себя как жидкость в обычном понимании этого

слова, и условия, когда жидкость механически неотличи

ма от твердого тела. Поставленный вопрос легко разре

шается, если ввести время релаксации для вязкой, нью

тоновской жидкости, которое равно отношению вязкости

к модулю сдвига, т„=^Т]/ц. Тогда для периодических

процессов с периодами Т > т„ тело будет вести себя как

жидкость, а для периодов Т < т„ — как твердое тело. Для

большинства жидких тел )]—1 пуаз, ц ~ 10“ дин/см2 и

т„ ~ 10~и с. Следовательно, в обычных условиях практи

чески всегда Т » т„, и мы имеем дело с проявлением жид

кого состояния, хотя в случае астеносферного слоя н

недрах Земли i} ~ 1021 пуаз, р, ~ 1012 дин/см2, т„ ~ 10э с,

и мы имеем дело с проявлением твердого состояния,

Т « т„.

В случае твердого состояния скорости Р- н 5-волн рав-

V v'T

пы vP = у

-----

и vs — у — . в случае жидкого со

стояния vp----- V vs = 0. Поэтому при переходе от вы-

2 л

сокпх частот, со » со,, — — , к низким, со < со„, модуль сдви-

тп

га меняется от своего высокочастотного значения ц(°°)до

низкочастотного ц(0), равного нулю для вязкой жидко*

сти, jLi(O) = 0. Максвелловским реологическим телом как

раз и будет вязкая жидкость, рассмотренная во всем ин

тервале частот. При коротких периодах оно проявляет

себя как твердое тело, а при длинных как жидкость. Ме-

хаиические свойства реальных твердых тел моделируются

более сложными реологическими моделями, в которых

модуль сдвига меняется от своего высокогочастотиого зна

чения (li(o°) до низкочастотного — статического значения

р(0), пе равного пулю. Таким образом, мы видим, что

при переходе от чисто упругих моделей Земли к неуп

ругим не зависящий от частоты высокочастотный модуль

сдвига |д(°°) следует заменить на динамический модуль

сдвига рд(а>), зависящий от частоты. До работы, опубли

кованной в 1975 г. С. Ц. Акопяном, В. 11. Жарковым и

В. М. Любимовым, это известное обстоятельство не ана

лизировалось, п чисто интуитивно предполагалось, что

частотная зависимость динамического модуля сдвига

слишком слаба, чтобы привести к наблюдаемым эф

фектам.

Оказалось, что учет частотной зависимости приводит

к заметному понижению модуля сдвига порядка 3—5%

при переходе от периодов ~1 с к периодам ~10 мин. в

зонах Земли с пониженными значениями Qv. Мы уже

отмечали, что пеучет этого обстоятельства, по существу,

обесценивает многие построения детальных моделей

Земли, когда речь идет об уточнении распределе

ний скоростей сейсмических воли порядка одного про

цента.

Тот факт, что современные реальные модели Земли

должны зависеть от частоты, проявился в последних

работах по этому вопросу следующим образом. Чтобы

согласовать модель Земли, построенную по данным о

собствешшых колебаниях (периоды ~10 мин.), с мо

делью, построенной но объемным волнам (периоды 1 с),

приходилось чисто формально вводить поправку отсчета

во времена пробега объемных волн. Физической причи

ной, из-за которой возникает эта поправка, является не-

уиругость земных недр. Теперь стало ясно, что необхо

димо перейти от старой концепции не зависящего от ча

стоты модуля сдвига и к более правильной концепции

динамического модуля сдвига Рд(ш), зависящего от ча

стоты, и при построении модели Земли вводить поправку

за динамический модуль сдвига земных недр, как это

описано ниже.

Выше отмечалось, что для горных пород и земных

недр слабо зависит от частоты или, быть может, вовсе

от нее не зависит. Конкретную зону Земли с заданным

чисто феноменологически можно описать некоторой

реологической моделью, называемой моделью Ломшхца,

которая в рассматриваемом интервале частот дает плато

для ()м(со). Тогда можно получить простую формулу для

изменения динамического модуля сдвига (т. е. поправку

за динамический модуль сдвига) при переходе от стан

дартной частоты со,, к некоторой произвольной частоте со.

Исходные модели Земли, применяемые при расчете

собственных частот, построены по объемным волнам, по

этому поправку за динамический модуль сдвига разумно

отсчитывать от значения рд (Т ~ 1 с),со0 = = 2л.Тог-

1 о

да поправка за динамический модуль сдвига для i-ro слоя

Земли ()„ = <2,,, равна

Д[.1д; (со. ЦД{ (СО, ^|xi) Ид! (t^o- ““

•> д_. со„

= ТГ1 1 » — - (41)

л <V ^ ы

где со0 = 2л, p,0i = РдДсоо, Qm) — динамический модуль

сдвига в г-м слое Земли для стандартной частоты (о„.

Поясним теперь более подробно, почему поправка за

динамический модуль сдвига снимает вопрос о поправ

ках отсчета, о которых мы уже упоминали выше. Поп

равками отсчета называются добавки к временам пробе

га S-, Р- и других типов волн, которые приходится делать

при построении моделей Земли, когда используются дан

ные как о временах пробега объемных волн, так и о пе

риодах собственных колебаний Земли. Величина этой по

правки At составляет 1—4 с (для 5-волн ~4 с, для Р-

волн ~2 с), т. е., чтобы согласовать модель с данными

о частотах собственных колебаний Земли, необходимо не

сколько «уменьшить» скорости объемных сейсмических

волн, что и увеличивает времена пробега с).

Именно этот эффект дает переход от идеально упругого

к динамическому модулю сдвига. Действительно, перио

ды собственных колебаний в 102 и 103 раз больше, чем

периоды объемных волн. Соответственно для них модуль

сдвига меньше (так сказать, модуль сдвига «мягче»). Ес

ли мы с этим модулем сдвига сосчитаем времена пробега

для объемных волн, то получим, що опн больше наблю

даемых примерно иа величину поправки отсчета \t ~

~ 1 + А с.

В действительности при построении моделей следует

отказаться от формального введения поправок отсчета и

действовать совсем иначе. За исходную следует выбрать

модель Земли, полученную по объемным волнам (высоко

частотная модель), и при совместном использовании вре

мен пробега и частот собственных колебаний вводить

для последних поправки за динамический модуль сдвига,

как ото описано выше.'Такой подход пе только болен

правилен с физических позиций, но и делает саму задачу

о моделях Земли более глубокой, тесно связывая распре

деление QtXD в Земле с распределением модулей упру

гости н плотности.

Само Qfil) можно определять отдельно от модели по

данным о затухании собственных колебаний и объемных

волн. Однако при построении модели Земли с учетом

поправок за динамический модуль сдвига хорошая согла

сованность данных об объемных волнах и собственных

колебаниях будет указывать, что принятые при расчете

распределения (?„(/) удовлетворяют также некоторым ин

тегральным условиям согласования обопх типов данных.

Переход от статического модуля сдвига к динамиче

скому открывает совершенно новые горизонты в исследо

вании неупругости земных недр на сверхдлинпых перио

дах, соответствующих приливным деформациям тела Зем

ли. Как известно (см. § 2.6), отклик Земли на приливное

возмущение характеризуют тремя безразмерными числа

ми Лява. Число h равно отношению высоты прилива уп

ругого тела Земли к высоте равновесного (статического)

океанического прилива на абсолютно твердой Земле. Чис

ло к равно отношению дополнительного потенциала, воз

никающего из-за приливной деформации Земли, к возму

щающему потенциалу. Наконец, число I представляет со

бой отношение горизонтального смещения при приливе к

такому же смещению при равновесном океаническом при

ливе па абсолютно твердой Земле. Кроме того, Земля ис

пытывает чапдлеровское колебание, возникающее из-за

того, что ось вращения Земли слегка наклонена к оси наи

большего момента инерции. Период чандлеровского коле

бания Тш = 4 3 4 4 3 5 ± (1—2) звездных суток, так же кап

и числа Лява h, к, I, является функционалом от распреде

ления плотности рШ, модуля сдвига ц(1) и модуля сжа

тия К(1) в земных недрах. А поскольку динамический

модуль сдвига цд((о) зависит от частоты, все указанные