Zee A. Quantum Field Theory in a Nutshell

Подождите немного. Документ загружается.

512 | Part N

Exercises

N.3.1 Show that the structure of Lie algebra (21) emerges naturally.

N.3.2 In appendix 1 we recursed by complexifying the momenta of two external lines with helicity + and −.

In the derivation of the recursion relation (3) we could have picked any two external lines to complexify.

Determine the amplitude calculated directly in chapter N.2, namely A(1

−

), by complexifying

lines 1 and 2. This is an example of the self-consistency argument sketched in the text.

Particle physics experimentalists are fond of saying that yesterday’s spectacular discovery is today’s

calibration and tomorrow’s annoying background. The canonical example is the Nobel-winning discovery

of the CP -violating decay of the K

meson into two pions. In theoretical physics, yesterday’s discovery is

today’s homework exercise and tomorrow’s trivium.

N.3.3 Using the explicit forms given for A(1

−

) and A(1

−

) in the preceding chapter,

check the estimated large z behavior in (13–15).

N.3.4 Worry about the sloppy handling of factors of 2 in appendix 1. [Hint: The final result is correct because

the polarization vectors in (5–6) are normalized to |ε|

= 2 for convenience.]

N.4

Is Einstein Gravity Secretly

the Square of Yang-Mills Theory?

Gravity and gauge theory

Quantum gravity has baffled generations of theoretical physicists, as you have no doubt

heard. One aspect of this puzzle is the relationship between gravity and gauge theory,

which describes the other fundamental interactions. While gravity and gauge theory are

both born of local invariance, the Einstein-Hilbert action



√

−gR and the Yang-Mills

action



xtr(F

μν

) look completely different.

Perturbatively, gravity is afflicted with an infinite number of interaction terms, as was

explained in chapter VIII.1, and hence gravity is not renormalizable, in stark contrast to

gauge theory. On the other hand, the two field theories enjoy many conceptual similarities

between them. Yang-Mills theory is the unique low energy effective theory of a spin 1

massless field, just as Einstein gravity is the unique low energy effective theory of a spin 2

massless field.

String theory unifies gravity and gauge theory. This remarkable fact alone points to a

deep connection between gravity and gauge theory, even though within field theory the

connection is totally obscure. One important clue is that the oscillator spectrum of the open

string contains only the gauge field but not the graviton, which appears in the spectrum

of the closed string. However, the closed string spectrum could be described as two copies

of an open string spectrum, thus leading Kawai, Lewellen, and Tye to discover relations

between graviton scattering and gauge boson scattering.

In the limit of the string energy

scale going to infinity, we know that string theory reduces to field theory and thus a shadow

of these KLT relations should survive in field theory. (As you might know, not all theorists

are convinced that string theory corresponds to reality. If string theory eventually fails,

its ultimate value might well turn out to be the light it sheds on the hidden structure of

quantum field theory.)

It is definitely beyond the scope of this book to explain these statements. See, for example, J. Polchinski,

String Theory, p. 27.

514 | Part N

In any case, the bottom line is that string theory strongly hints that graviton ampli-

tudes can be expressed as products of Yang-Mills amplitudes, schematically M

gravitons

∼

gauge

× M

gauge

. The first reaction of many theoretical physicists when first told this

is puzzled skepticism. How is this possible, they ask quite reasonably, since Yang-Mills

contains an internal symmetry group while gravity doesn’t?

Now that we have learned to strip color, a connection between amplitudes no longer

strikes us as so implausible, particularly if we stick to on-shell scattering amplitudes for

gluons in specified polarization states M

...

, namely amplitudes that experimentalists

can measure, rather than amplitudes M

...

carrying Lorentz indices that theorists

using traditional methods play with. As we saw in the preceding chapter, the color stripped

tree-level on-shell helicity amplitude for gauge boson scattering boils down to the 

...



and [

...

] products of two component spinors. We did not do the analogous calculation of

the tree-level on-shell helicity amplitude for graviton scattering, but we could anticipate

that the result would again be expressed in terms of the 

...

 and [

...

] products. The

spinor helicity formalism is intrinsic to the Lorentz group SO(3, 1), not tied to a specific

theory. In particular, the interaction vertices in Einstein gravity are again given in terms

of scalar products of momenta and polarization vectors. Quite suggestively, the graviton

polarization vectors can be written, as mentioned in appendix 1 to the preceding chapter,

as 

μν

= 



, a product of the gauge theory polarization vectors.

Indeed, I have already given part of the mystery away in the preceding chapter. We saw

that the basic cubic interaction vertex of three gravitons (with complex momenta) is given

by the square of the corresponding quantity for three gluons.

In summary, thanks to our string theory friends, we now know that there exists a

secret structural connection between gravity and gauge theory that is totally opaque at

the Lagrangian level.

Deformed graviton polarizations

In this closing chapter, I give a brief introduction to the exciting quest for this secret

connection. I will be content to look at one specific calculation.

Go back to the BCFW recursion (chapter N.3). It would work for gravity if the com-

plexified scattering amplitude M(z) vanishes as z →∞. But naively, it would seem that

the situation for gravity is even worse than the situation for gauge theory, since the cubic

graviton vertex is quadratic in momentum and thus goes like z

. (Recall the two powers

of derivative in the scalar curvature; see chapter VIII.1.) Repeat the calculation in the pre-

ceding chapter for n-graviton on shell scattering. Go back to figure N.3.2 and interpret the

lines as gravitons. The (n − 2) cubic vertices give a factor of z

2(n−2)

for large z, easily over-

whelming the factor of 1/z

n−3

from the (n − 3) propagators. This nasty behavior occurs

even before we include the polarization of the two hard gravitons.

The graviton carries helicity ±2 (appendix 2 of chapter VIII.1) and hence a polarization

“vector” 

μν

, given by a symmetric and traceless tensor. We can naturally construct 

μν

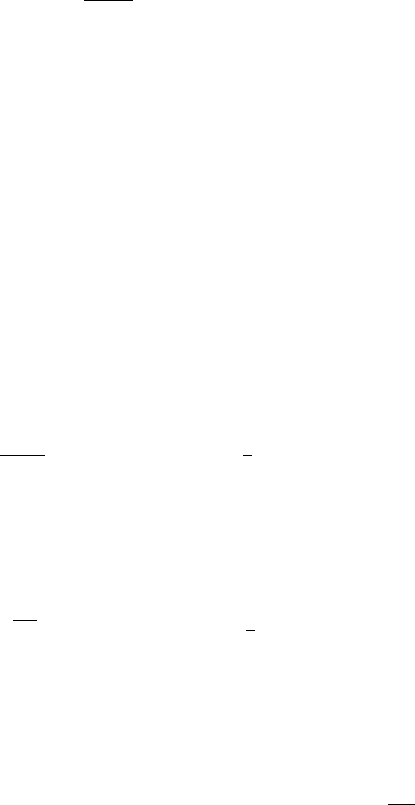
N.4. Gravity and Yang-Mills Theory | 515



out of the polarization vectors for a massless spin 1 particle (as already explained in

the preceding chapter). Thus, after deformation,



++μν

(z) = 

+μ



+ν

= (q

∗

+ zp

)

∗

+ zp

)

, 

−−μν

(z) = 

−μ



−ν

= q

(1)

and



++μν

(z) = 

+μ



+ν

= q

, 

−−μν

(z) = 

−μ



−ν

= (q

∗

− zp

)

∗

− zp

)

(2)

Note that the 

μν

(z)’s are in fact traceless and could go as either z

or z

for large z.

Putting it together, we obtain the naive estimate

−−, ++

naive

(z) →

2(n−2)

n−3

= z

n−1

, M

−−, −− or ++, ++

naive

(z) → z

n+1

, M

++, −−

naive

(z) → z

n+3

(3)

The escalating behavior as n increases is the hallmark of a nonrenormalizable theory, as

explained in chapter III.2.

Hard graviton in a soft spacetime

Once again, we hope that real life is cushier than naive expectation. By the same reasoning

used for gauge theory, we study a hard graviton blasting through a gravitational field, that

is, a background of soft gravitons. So write the metric of spacetime as G

μν

= g

μν

+ h

μν

Plug this into the Einstein-Hilbert action (VIII.1.1) and extract the terms quadratic in h.

While the calculation is straightforward, it does involve some heavy lifting. To avoid the

labor, we note that using the harmonic gauge, we did this calculation in (VIII.1.10) but

only for the special case g

μν

= η

μν

(in other words, we expanded around flat Minkowski

spacetime rather than a general curved spacetime). We had

L =

64πG

(η

μν

λρ

στ

∂

λσ

∂

ρτ

−

μν

∂

h∂

h) (4)

with the trace degree of freedom h ≡ η

μν

. Henceforth, we set 64πG = 1.

Armed with symmetry considerations and our knowledge of gravity (chapter VIII.1), we

can almost immediately guess that when we go from a flat η

μν

to a curved g

μν

background,

this quadratic Lagrangian generalizes to

L =

√

−g(g

μν

λρ

στ

λσ

ρτ

−

μν

h − 2R

λρ σ τ

λσ

ρτ

) (5)

with h now defined as h ≡ g

μν

. Here D denotes the covariant derivative with respect

to the curved metric g

μν

introduced in chapter VIII.1 and R

λρ σ τ

the Riemann curvature

tensor constructed out of g

μν

. I trust you not to confuse this D associated with the

curved background with the covariant derivative in Yang-Mills theory used in the preceding

chapter and mentioned below in passing.

Let us go through the various features of (5). The

√

−g goes with the spacetime volume

and is common to any Lagrangian in curved spacetime, as we learned way back in (I.11.2).

We also learned there to promote any Lagrangian from flat to curved spacetime by replacing

μν

with g

μν

and the ordinary derivative by a covariant derivative (see chapter IV.5). As you

516 | Part N

can see, everything pretty much works out in parallel with how things work out for gauge

theory. The new feature is the term involving the Riemann curvature tensor R

λρ σ τ

, which

vanishes upon restriction to flat spacetime. But you are not surprised that such a term

could pop up, given trF

μν

, a

] in (N.3.8). Indeed, the only thing we can’t determine

without doing the actual calculation is the numerical coefficient (−2) of this term. That

particular number will play no role in the following discussion.

Also, in the preceding chapter we dropped a term linear in a

because of the equation

of motion D

μν

= 0. Here, analogously, we dropped a term linear in h

μν

because of

Einstein’s equation of motion R

μν

= 0. This also explains why terms involving the Ricci

tensor R

μν

and the scalar curvature R do not appear in (5).

We want to calculate the large-z behavior of various scattering amplitudes M

−−, ++

etc., and compare with the naive expectation (3). We hope that the same trick we used

for the gauge theory case would also work for gravity. Now the string theory hint, that

gravitons

∼ M

gauge

× M

gauge

, suggests a factorized structure in the graviton amplitude,

and so more or less naturally leads to the guess that the first index λ and the second index

σ of h

λσ

are somehow associated respectively with the two copies of M

gauge

The key to breaking the problem apart is the Bern transformation unlinking these two

indices. Examining (5), we see that the only term that links the first index with the second

index of h

λσ

appears in the term g

μν

h, since h = g

μν

does precisely that. How

to get rid of this term? The trick, following Bern and Grant, is to introduce a scalar field φ

and add the term 2g

μν

∂

φ∂

φ. We are allowed to do this, since φ does not appear in the tree

level graviton scattering amplitude we are studying. (Of course, the theory is changed from

pure gravity, and φ does circulate in loop diagrams for graviton scattering. Some readers

may also know that in string theory the graviton appears with a scalar φ, the experimentally

unobserved dilaton.)

For pedagogical clarity in explaining what we are going to do next, it is best to retreat

to the case of the flat background. Focus on the parenthesis in (4), now modified to

(∂

λσ

∂

λσ

−

∂

h∂

h + 2∂

φ∂

φ). (The normalization of φ is, in this context, just

chosen for convenience.) Since we can always make a field redefinition (see the appendix to

chapter VIII.3) without affecting on-shell scattering amplitudes, we let h

λσ

→h

λσ

+η

λσ

(and hence h → h + 4φ) and φ → φ +

h. You can verify that our parenthesis changes to

(∂

λσ

∂

λσ

− 2∂

φ∂

φ). Since in this manipulation the role of η

λσ

is merely to convert

λσ

into h, the same transformation works when η

λσ

is promoted to g

λσ

The upshot is that we can effectively rewrite (5) as

L =

√

−g(g

μν

λρ

στ

λσ

ρτ

− 2R

λρ σ τ

λσ

ρτ

) (6)

Now that φ has done his job, we have unceremoniously thrown him out since he doesn’t

contribute to the on-shell tree amplitudes we are interested in. We have thus dropped the

term g

μν

∂

φ∂

φ.

There has been quite a bit of formal development and perhaps the reader has lost sight

of what we are trying to do. Recall that we want to study the amplitude of a hard graviton

blasting through spacetime. Although a multitude of indices have appeared, as is always

the case with gravity, you should recognize that this Lagrangian is conceptually simple: it

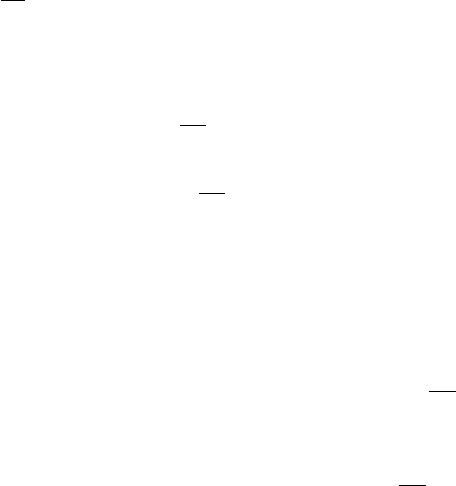
N.4. Gravity and Yang-Mills Theory | 517

is quadratic in the quantum field h describing the hard graviton and contains some given

c-number tensors g

λρ

(x) and R

λρ σ τ

(x) pertaining to the background.

Unlinked melody

The important point is that the two indices carried by h

λσ

are now unlinked from each

other in the first term in (6). In chapter VIII.1, we learned to trade a “world index” like

λ for a locally flat Lorentz index a by using the vierbein e

(x). Here we are invited to

introduce two sets of vierbein, e and ˜e, with their associated connections ω and ˜ω, and

write h

λσ

≡e

˜e

˜a

a ˜a

. In reality, of course e =˜e and ω =˜ω, but this notation keeps track of

the fact that the two sets of indices carried by h

λσ

are unlinked. Note that h

λσ

is treated in

our quadratic Lagrangian as just some tensor field living in a curved spacetime specified

by g

λσ

≡ e

˜e

˜a

a ˜a

Also in chapter VIII.1 we emphasized that the covariant derivative acting on vectors

carrying a world index and on vectors carrying a locally flat Lorentz index assumes different

forms, D

= ∂

− 

μν

and D

= ∂

− ω

μa

, respectively. For pedagogical

clarity, I will use two different symbols D and D to denote what is conceptually the same

operation. For our problem we have D

μν

˜e

˜a

a ˜a

, with D

a ˜a

=∂

a ˜a

−ω

λa

b ˜a

−

˜ω

λ ˜a

With this notation, the relevant Lagrangian becomes

L =

√

−g(g

μν

˜η

˜a

a ˜a

− 2R

ab˜a

a ˜a

) (7)

We are now ready to study the large z behavior of the scattering amplitude of a hard graviton

carrying momentum zq +

...

blasting through a curved background spacetime g

μν

The analysis proceeds much as in the Yang-Mills case discussed in the preceding chap-

ter. Focus on the first term:

√

−gg

μν

˜η

˜a

(∂

a ˜a

− ω

μa

c ˜a

−˜ω

˜c

μ ˜a

a ˜c

)(∂

− ω

νb

−

˜ω

). The leading O(z

) behavior comes from the piece containing two derivatives in

the first term, namely L

lead

≡

√

−gg

μν

˜η

˜a

∂

a ˜a

∂

, and thus contributes to the am-

plitude a term proportional to η

˜η

˜a

. In the Yang-Mills case, the Lagrangian contains a

hidden “enhanced Lorentz” symmetry. Here the situation is even better: we have not one,

but two hidden “enhanced Lorentz” symmetries. The term L

lead

is evidently left invariant

by two separate SO(3, 1) Lorentz transformations, one operating on the a, b indices, the

other on the ˜a ,

b indices.

The subleading O(z) behavior comes from the pieces in the first term containing one

derivative and one factor of either ω or ˜ω, for example

√

−gg

μν

˜η

˜a

∂

a ˜a

(ω

νb

˜ω

). In this way we find that M

ab, ˜a

→ cz

˜η

˜a

+ z(η

˜a

+ A

˜η

˜a

) +

...

, with

and

˜a

two matrices antisymmetric in their indices. To see this, consider for example

the piece involving ω (after some relabeling of indices):

√

−gg

μν

˜η

˜a

(∂

a ˜a

)ω

νc

. This

gives rise to the term A

˜η

˜a

in M

ab, ˜a

. Note that since the matrix A

depends on the

spin connection ω

of the background, all we can say is that it is antisymmetric in its two

indices ab. Recall that this is quite analogous to what we did in the Yang-Mills case.

518 | Part N

Before reading further, you could now flex your mental muscle and push ahead to

obtain the sub-subleading O(z

) behavior. This comes from the pieces in the first term

containing two factors of ω and ˜ω, for example (again, after some relabeling of indices)

√

−gg

μν

˜η

˜a

μc

a ˜a

νd

. All we can now conclude is that this contributes to the scat-

tering amplitude a term of the form B

˜η

˜a

, with B

an arbitrary matrix. To this order,

the second term in (7) also contributes, breaking the “enhanced Lorentz” symmetries com-

pletely. Nevertheless, we can still exploit the known symmetry properties of the Riemann

curvature tensor under interchange of its indices to say something about its contribution

to the scattering amplitude. Putting it all together we conclude that

ab, ˜a

→ cz

˜η

˜a

+ z(η

˜a

+ A

˜η

˜a

) + A

ab˜a

+ (η

˜a

+ B

˜η

˜a

) + O





(8)

Compare this with (N.3.12), which states that the amplitude for the scattering of a hard

gluon off a background of soft gluons goes like M

=(cz +

...

)η

...

Amazingly, you can see that the large-z behavior for the scattering of a hard graviton off a

background of soft gravitons can be obtained by “squaring” the large-z behavior for the

scattering of a hard gluon off a background of soft gluons! In other words, M

ab, ˜a

∼

˜a

, as far as the large-z behavior is concerned.

Just as in the Yang-Mills case, by exploiting gauge identities like p

(z)M

a ˜a , b



(z) =

0, we can determine the large-z behavior of various helicity amplitudes. For your conve-

nience I remind you that (from the preceding chapter) p

(z) = p

+ zq and p

(z) = p

−

zq. Thus the gauge identity just displayed says that q

a ˜a , b



(z) =

−(1/z)p

a ˜a , b



(z). Recalling [see (1)] that 

−−μν

(z) = q

we see that in calcu-

lating the amplitude M

−−, h

(z) we can effectively replace 

−−μν

(z) by (1/z

. Thus

we can immediately conclude, since 

++μν

(z) ∼ z

for large z [see (2], that for example

−−, ++

(z) →

(9)

which is far better than the naive expectation M

−−, ++

naive

(z) → z

n−1

. Indeed, the horrible

ever-escalating behavior with increasing n has disappeared. Even more remarkably, the

large-z behavior of graviton scattering amplitudes is consistent with the string-inspired

notion that gravity is “the square of Yang-Mills.” Recall that in gauge theory M

−+

(z) →1/z.

Thus, for large z, indeed M

−−, ++

(z) ∼ (M

−+

(z))

The bottom line here is that the large-z behavior of gravity is surprisingly benign and

vanishes fast enough for the recursion program to work.

Gravity is a square?

So, is Einstein gravity secretly the square of Yang-Mills theory?

Already we have seen in the preceding chapter, anticipating that the recursion pro-

gram works, that the primitive 3-point amplitude for gravity (for one helicity configura-

tion) (12

/2331)

is the square of the primitive 3-point amplitude for gauge theory

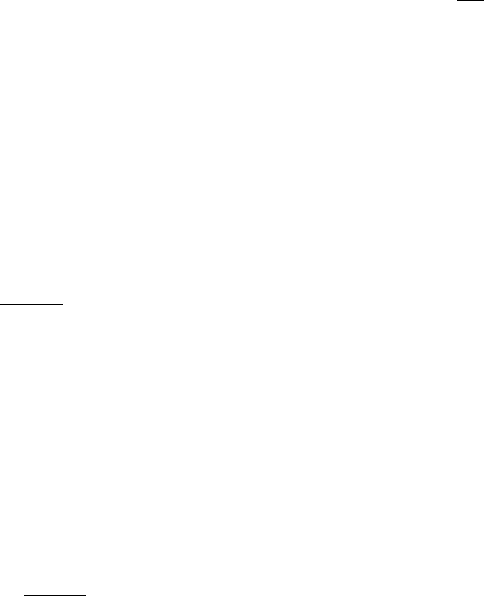
N.4. Gravity and Yang-Mills Theory | 519

(12

/2331), something that you could have never suspected by staring at

√

−gR and

trF

μν

untill you are blue in the face.

The calculations in the previous section show that the large-z behavior for the scattering

of a hard graviton off a background of soft gravitons could be obtained by “squaring” the

large z behavior for the scattering of a hard gluon off a background of soft gluons, certainly

something that nobody could have anticipated by looking at Lagrangians.

Further evidence that the answer to the title of this chapter is “yes” comes from a recent

calculation by Bern, Carrasco, and Johansson. Interestingly, they do not strip the color

from a Yang-Mills theory, but instead show that they can write the “color-dressed” tree

amplitudes in the form

tree

(1, 2,

...

, n) =



(

)

(10)

It is beyond the scope of this book to explain in detail how this expression is obtained. I

merely state that the index a labels an individual diagram. For each diagram, the amplitude

may be written as the product of a kinematic function n

of the momenta and a color factor

, divided by the product of the momenta p

carried by the internal lines. (I do not explain

here how n

and c

are defined.) The tree amplitude is then given by a sum over all tree

diagrams.

Bern et al. then conjecture that the n-graviton scattering amplitude at the tree level is

given, amazingly, by

tree

gravity

(1, 2,

...

, n) =



(

)

(11)

They have checked by explicit computation that their conjecture in fact holds up to n = 8.

Furthermore, they have also verified that the conjecture, suitably generalized, also holds

for the various supercousins of Einstein gravity and Yang-Mills theory.

Thus the evidence is extremely strong that, yes indeed, Einstein gravity is secretly the

square of Yang-Mills theory, at least at the level of tree amplitudes. However, as of this

writing (February 2009), there is no definitive understanding within field theory. The final

word on the subject has yet to be said, and it is not even clear what the final path to the final

word might be. I would be foolish indeed to discuss this further in a textbook when the

entire subject is being rapidly developed. By the time this book is published, the conjecture

that Einstein gravity is the square of Yang-Mills theory may well have been proved. If not,

then nothing would please me more than if a reader of this textbook could go on and prove

it, hopefully not just at the tree level, but to all orders.

What is the simplest field theory?

The uninitiated would likely answer ϕ

theory. Indeed, field theory texts almost all start with

some kind of scalar field theory. Even I am not able to do any better. But the sophisticated,

namely you, now that you have reached the end of this text, realize that the more symmetry

the theory has the better. To theoretical physicists, simplicity actually secretly means

520 | Part N

symmetry. Incidentally, I have always hated scalar field theories, and have ventured to

say so publicly. It is hard to like the action L =

(∂ϕ)

−λϕ

, so barren of color and flavor.

Some of the major problems facing particle physics, such as the hierarchy problem, may

eventually turn out to stem from our not having mastered scalar field theory.

Of course, scalar field theory is the simplest in the superficial sense that you need to

know the least to approach it. As I said in chapter I.12, once one is familiar with scalar

field theory the rest consists of “merely” decorating the field with various indices describing

spacetime or internal symmetries. But the symmetry and the resulting structure provide

us with handles to grab on to. Both Yang-Mills theory and Einstein gravity have an internal

logic sorely lacking in scalar field theory. As I mentioned in chapters VII.3 and VIII.4,

the consensus view is that the first exactly soluble field theory would almost certainly be

N = 4 supersymmetric Yang-Mills theory, the supercousin of pure Yang-Mills theory. The

remarkable recent developments described in the last three chapters have only reinforced

this view. Almost beyond belief, even gravity may be simpler than we had long thought.

For large complexified momentum, graviton scattering for some helicity arrangements

actually behaves better than gluon scattering. The evidence is mounting that Einstein

gravity may in some sense be the square of Yang-Mills theory. So now we are left with the

amusing thought that the simplest field theory may well end up being gravity or N = 8

supergravity with its maximal supersymmetry. (At this point, a friend of mine who works

with N =8 supergravity pipes up, “It sure doesn’t look simpler if you are the guy doing

the calculation!” It is clear from the simple dimensional argument of chapter III.2 that

as one goes to higher order, the numerator of the Feynman integrand quickly becomes

extremely involved.)

Only time will tell who will win the simplest field theory contest, but we do have two

convincing candidates.

More Closing Words

In the closing words to the first edition of this book, I wrote that Yang-Mills theory

was almost begging for a better notation that would lay bare the deeper structure of the

theory. Oy, the excess baggage we have to carry! Ten thousand terms instead of one. In

some respects, the spinor helicity formalism and the recursion program explained in

chapters N.2–N.4 provide a partial answer to that pious wish.

Imagine some theorist idly wondering, after 1865, if there were a better notation to

describe the six fields E

, E

, B

for which Maxwell had written 20 equations

(since he did not use vector notation). We can even fantasize that by fooling around with

numerology (“Look, 4

3/2 = 6!”), this “crackpot” came up with an antisymmetric 4 by 4

matrix he called F . Shoehorning Maxwell’s equations in vacuum (some of them stating

that the time variation of E and B is related to the space variation of E and B) into this

strange notation, this guy could even stumble on a secret connection between space and

time.

The spinor helicity formalism and the recursion program, though elegant, are still

rooted in the perturbative expansion of the 1940s. Can they be pushed into the nonpertur-

bative regime? There have been attempts in that direction.

In all previous revolutions in physics, a formerly cherished concept has to be jettisoned.

If we are poised before another conceptual shift, something else might have to go. Lorentz

invariance, perhaps? More likely, we may have to abandon strict locality. Again, in closing

words I mumble something (from steepest descent to integral to what?) about modifying

the form of the path integral. The recursion program and the resuscitated S-matrix ap-

proach might be a step in this direction, formulating field theory while avoiding mention

of a local Lagrangian. But we need analyticity, and of course analyticity follows from local-

ity and causality, as far as we understand. We know also that even local field theory could

spawn non-local constructs, most notoriously the horizon of a black hole. But there the