Zee A. Quantum Field Theory in a Nutshell

Подождите немного. Документ загружается.

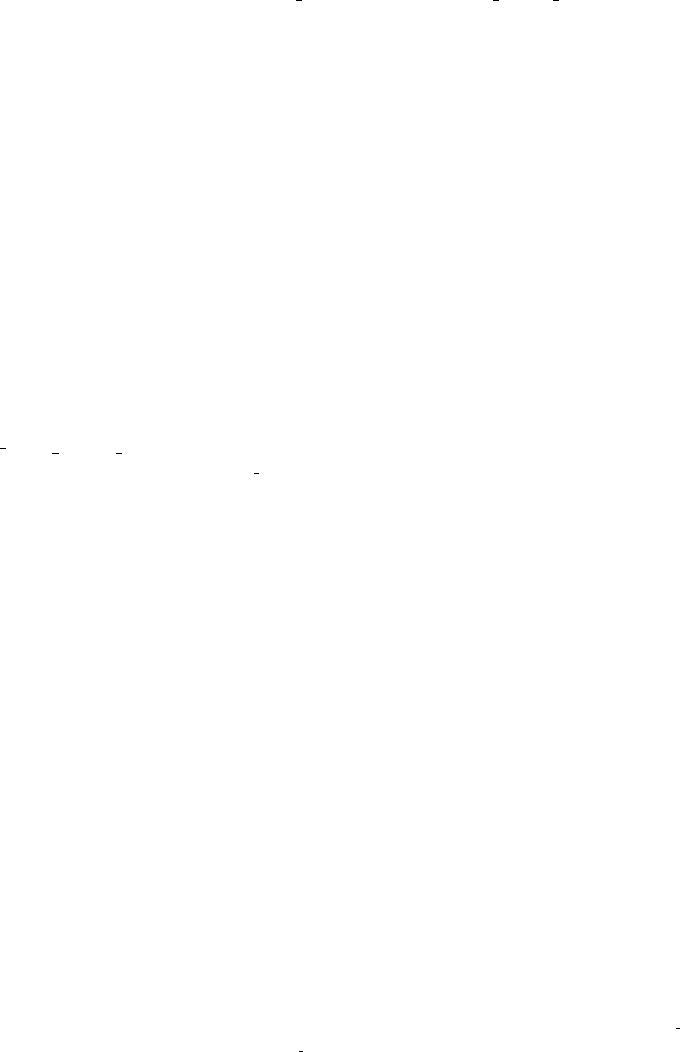
532 | Appendix B. Brief Review of Group Theory

ϕ to point along the third axis, in which case e

ϕ



is diagonal with elements e

and e

−

. Thus, while the matrix

is not unitary, its determinant is manifestly equal to 1.) This set of matrices defines the multiplicative group

SL(2, C), consisting of all 2 by 2 complex-valued matrices with unit determinant.

Let us count the number of generators of this group. Two conditions on the determinant (real part = 1,

imaginary part = 0) cut the four complex entries containing eight real numbers down to six numbers, which

accounts for the six generators of the Lorentz group SO(3, 1).

To exhibit the map explicitly, we extend the earlier discussion showing that SU(2) covers SO(3). Consider the

most general 2 by 2 hermitean matrix

= x

I −x

σ =



− x

− ix

+ ix

+ x



(31)

By explicit computation, detX

= (x

)

−x

. (To see this instantly, choose x to point along the third axis

and invoke rotational invariance.) Now consider X



= L

†

L, with L an element of SL(2, C). Manifestly,

detX



= detX

and thus the transformation preserves (x

)

−x

and hence corresponds to Lorentz transfor-

mations. Since L and −L give the same transformation x → x



, we see that SL(2, C) double covers SO(3, 1).

Mathematicians say that SO(3, 1) = SL(2, C)/Z

.IfL is also unitary, then x

0

= x

and the transformation is

a rotation. The SU(2) subgroup of SL(2, C) double covers the rotation subgroup SO(3) of the Lorentz group

SO(3, 1), that is, SO(3) = SU(2)/Z

Incidentally, if we introduce an i at a strategic location and define the 2 by 2 matrix X

I +i x

σ , regarding

(x , x

) as a 4-dimensional vector, we have detX

= (x

)

+x

, the Euclidean length squared of the 4-vector.

(Once again, choose x to point along the third axis so that X

is a diagonal matrix with elements x

±ix

.) Since



=cos

+i sin

(

σ)with

θ a unit vector in the θ direction (to see this, once again choose



θ to point along

the 3

axis), we see that X

/((x

)

+x

)

is an element of SU(2). (We will come back to this observation in the

next section.) Thus, for any two elements U and V of SU(2), the matrix X



= V

†

U can also be decomposed

in the form X



= x

4

I + i x



σ . Evidently, detX



= detX

. Thus the transformation preserves (x

)

+x

and

describes an element of SO(4). This shows explicitly that SO(4) is locally isomorphic to SU(2) ⊗ SU(2).If

V = U , we have a rotation, and if V

†

= U , the Euclidean analog of a boost.

Note that while the rotation group SO(3) is compact, the Lorentz group SO(3, 1) is not, since the range of

the boost parameters ϕ is unbounded. In contrast, the group SO(4) is compact and thus can be covered by a

compact group, namely, SU(2) ⊗ SU(2), but the noncompact group SO(3, 1) cannot be.

At this point, having done SO(4) and SO(3, 1), I might as well (with a wink toward the nuts who complained

that this book is not encyclopedic enough) throw in the group SO(2, 2) for use in part N. Let us strip the Pauli

matrix σ

(kind of a “troublemaker” or at least an odd man out) of his i and define (just for this paragraph)

≡



0 −1



Any real 2 by 2 matrix X

could be decomposed as X

I +x

σ . Now detX

=(x

)

+(x

)

−(x

)

−(x

)

the quadratic form of a spacetime with two time and two space coordinates. The set of all linear transformations

(with unit determinant) on (x

, x

) that preserve this quadratic form defines the group SO(2, 2).

Introduce the multiplicative group SL(2, R) consisting of all 2 by 2 real-valued matrices with unit determinant.

For any two elements L

and L

of this group, consider the transformation X



= L

. Evidently, detX



detX

. This shows explicitly that the group SO(2, 2) is locally isomorphic to SL(2, R) ⊗SL(2, R). Although two-

timing theories are bound to be trouble, we could use SO(2, 2) formally in computing scattering amplitudes, as

we will see in chapter N.3.

Topological quantization of helicity

As promised, let us go back to the observation in the previous section that the matrix X

/((x

)

+x

)

is an

element of SU(2). Define w

≡x

/((x

)

+x

)

for A = 1, 2, 3, 4. An arbitrary element of SU(2) can be written

as U = w

I + i w

σ , with det U = 1 = (w

)

+w

. The 4-dimensional unit vector w = (w

, w) traces out the

3-sphere S

, the surface of the 4-ball B

living in 4-dimensional Euclidean space. Thus the group manifold of

SU(2) is S

Next, recall that SU(2) double covers the rotation group SO(3), or in plain talk, two elements U and −U of

SU(2) corresponds to the same rotation. Thus the group manifold of SO(3) is S

, that is, the 3-sphere with

antipodal points identified.

Appendix B. Brief Review of Group Theory | 533

Consider closed paths in SO(3). Starting at some point P on S

, wander off a bit and come back to P . The

path you traced can evidently be continuously shrunk to a point. But suppose you go off to the other side of

the world and arrive at −P , the antipodal point of P . You also trace a closed path in SO(3) since P and −P

correspond to the same element of SO(3), but this closed path obviously cannot be shrunk to a point. On the

other hand, if after arriving at −P you keep going and eventually return to P , then the entire path you traced

can be continuously shrunk to a point. Using the language of homotopy groups introduced in chapter V.7, we

say that 

(SO(3)) = Z

: there are two topologically inequivalent classes of paths in the 3-dimensional rotation

group.

Now we can go back and tie up a loose end in chapter III.4. Back in school you learned that the nonlinear

algebraic structure of the Lie algebra [J

, J

] =i

ij k

enforces quantization of angular momentum. But the little

group for a massless particle is merely O(2). In the “rich man’s approach” to gauge invariance, how do we get

the helicity of the photon and the graviton quantized?

The answer is that we invoke topological, rather than algebraic, quantization. A rotation through 4π is

represented by e

i4πh

on the helicity h state of the massless particle, but the path traced out by this rotation

can be continuously shrunk to a point. Hence, we must have e

i4πh

= 1 and h = 0, ±

, ±1,....

Appendix C Feynman Rules

Here we gather the Feynman rules given in various chapters.

Draw all possible diagrams. Label each line with a momentum. If applicable, also label each line with an

incoming and an outgoing Lorentz index (for a line describing a vector field), with an incoming and an outgoing

internal index (for a line describing a field transforming under an internal symmetry), so on and so forth.

Momentum is conserved at each vertex. Momenta associated with internal lines are to be integrated over with

the measure



p/(2π)

]. A factor of (−1) is to be associated with each closed fermion loop. External lines

are to be amputated. For an incoming fermion line write u(p, s) and for an outgoing fermion line ¯u(p



, s



For an incoming antifermion, write ¯v(p, s), and for an outgoing antifermion, v(p



, s



). If there are symmetry

transformations leaving the diagram invariant, then we have to worry about the infamous symmetry factors.

Since I don’t trust the compilations in various textbooks I work out the symmetry factors from scratch, and that

is what I advise you to do.

Scalar field interacting with Dirac field

L =

ψ(iγ

∂

− m)ψ +

[(∂ϕ)

− μ

] −

+ fϕ

ψψ (1)

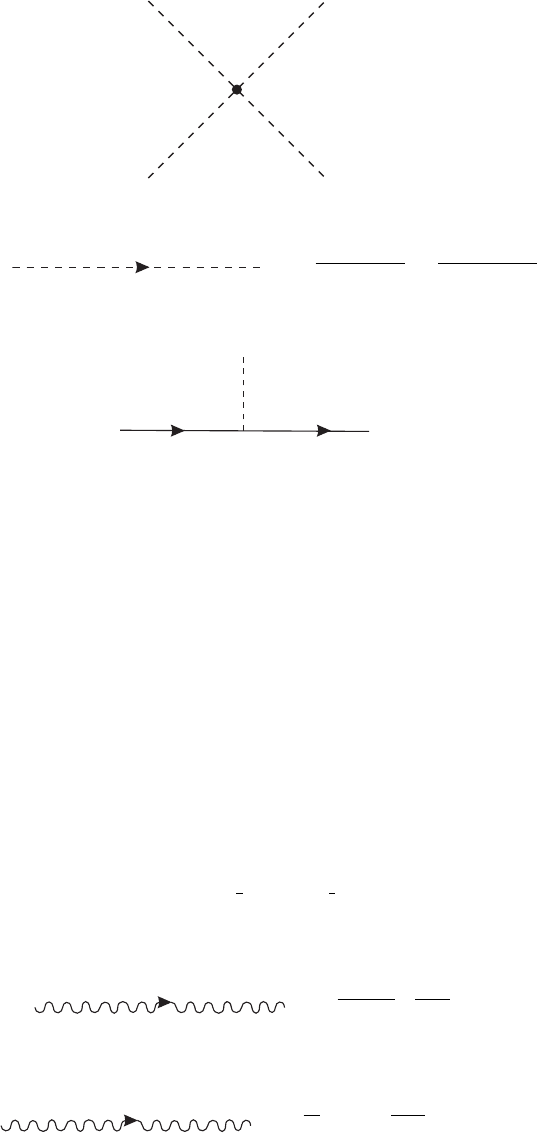
Scalar propagator:

− μ

+ iε

(2)

Appendix C. Feynman Rules | 535

Scalar vertex:

−iλ (3)

Fermion propagator:

p − m + iε

= i

p + m

− m

+ iε

(4)

Scalar fermion vertex:

if (5)

Initial external fermion:

u(p, s) (6)

Final external fermion:

¯u(p, s) (7)

Initial external antifermion:

¯v(p, s) (8)

Final external antifermion:

v(p, s) (9)

Vector field interacting with Dirac field

L =

ψ(iγ

(∂

− ieA

) − m)ψ −

μν

−

(10)

Vector boson propagator:

− μ



− g

μν



(11)

Photon propagator (with ξ an arbitrary gauge parameter):



(1 − ξ)

− g

μν



(12)

536 | Appendix C. Feynman Rules

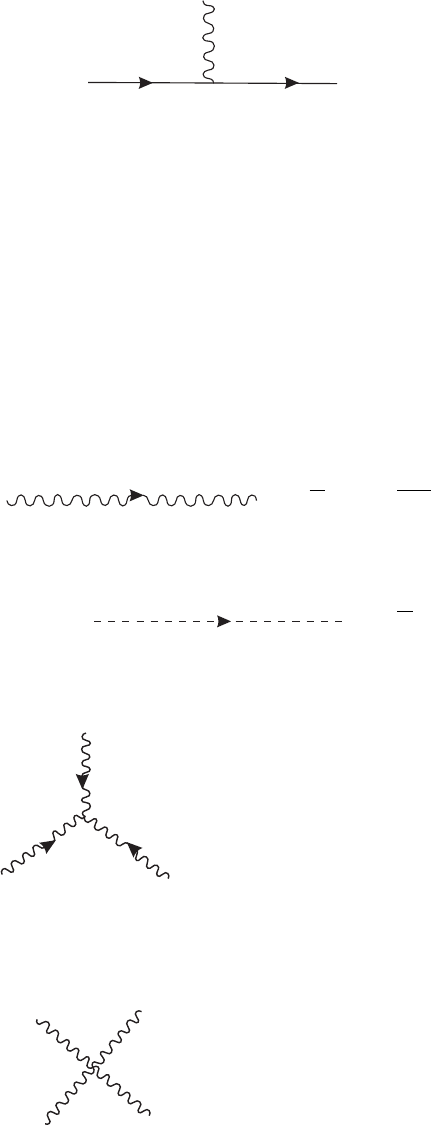
Vector boson fermion vertex:

ieγ

(13)

Initial external vector boson:

(k) (14)

Final external vector boson:

(k)

∗

(15)

Nonabelian gauge theory

Gauge boson propagator:



(1 − ξ)

− g

μν



(16)

Ghost propagator:

(17)

Cubic interaction between the gauge bosons:

c,λ

b,ν

abc

μν

− k

)

+ g

νλ

− k

)

+ g

λμ

− k

)

] (18)

Quartic interaction between the gauge bosons:

b,ν

d,ρ

c,λ

− ig

abe

cde

μλ

νρ

− g

μρ

νλ

)

+ f

ade

cbe

μλ

νρ

− g

μν

ρλ

)

+ f

ace

bde

μν

λρ

− g

μρ

νλ

)]

(19)

Appendix C. Feynman Rules | 537

Gauge boson coupling to the ghost field:

abc

(20)

Cross sections and decay rates

Given the Feynman amplitude M for a process p

+ p

→ k

+ k

...

+ k

the differential cross section is

given by

dσ =

|v

−v

|E(p

)E(p

)

(2π)

E(k

)

...

(2π)

E(k

)

(2π)

(4)

+ p

−



i=1

)|M|

(21)

Here v

and v

denote the velocities of the incoming particles. The energy factor E(p) = 2



p

+ m

for bosons

and E(p) =



p

+ m

/m for fermions come from the different normalization of the creation and annhilation

operators in chapters I.8 and II.2.

For a decay of a particle of mass M the differential decay rate in its rest frame is given by

d =

(2π)

E(k

)

...

(2π)

E(k

)

(2π)

(4)

(P −



i=1

)|M|

(22)

Appendix D Various Identities and Feynman Integrals

Gamma matrices

Identities for the trace of a product of an even number of gamma matrices:

trγ

= 4η

μν

(1)

trγ

= 4(η

μν

λσ

− η

μλ

νσ

+ η

μσ

νλ

) (2)

We define the totally antisymmetric symbol ε

μνλσ

by ε

0123

=+1 (note ε

0123

=−1). Then with our definition

≡ iγ

, we have

trγ

=−4iε

μνλσ

(3)

Identities that follow from the basic Clifford identity:

pγ

=−2 p (4)

p  qγ

= 4p

q (5)

p q rγ

=−2 r q p (6)

I leave it to you to derive these identities. For example, to obtain (4) keep moving γ

to the right in the expression

pγ

= (2p

−pγ

)γ

= 2 p − 4 p =−2 p.

Evaluating Feynman diagrams

Over the years, a number of tricks and identities have been developed for evaluating the integrals associated with

Feynman diagrams.

Let us evaluate

I =



(2π)

− m

+ iε)



(2π)



2π

− (



+ m

) + iε]

Focus on the k

integral. Draw where the poles are in the complex k

-plane and you will see that the integration

contour can be rotated anticlockwise so that [we denote the integrand by f(k

)]



+∞

−∞

f(k

) =



+i∞

−i∞

f(k

) = i



+∞

−∞

f(ik

) (7)

Appendix D. Identities and Feynman Integrals | 539

where in the last step we define k

=ik

(corresponding to the Wick rotation mentioned in chapters I.2 and V.2.)

Thus,

I = i(−1)



(2π)

+ m

)

where d

k is the integration element in Euclidean 4-dimensional space and k

≡k



the square of a Euclidean

4-vector. The infinitesimal ε can now be set equal to zero. We can integrate immediately over the three angles

since the integrand does not depend on them. You can look up the angular element in Euclidean space in a book,

but we will use a neat trick instead.

I will do the more general d-dimensional integral H =



kF(k

), where k

...

and F can

be any function as long as the integral converges. (I now drop the subscript E; the context makes clear that we

are in Euclidean space.) We can of course set d equal to 4 at the end. The result for arbitrary d will be useful to

us in regularizing dimensionally (chapter III.1).

We imagine integrating over the (d − 1) angular variables to obtain H = C(d)



∞

d−1

F(k

). To determine C(d) we will do the integral J =



−

in two different ways. Using (I.2.8) we

have J = (

√

2π)

. Alternatively,

J = C(d)



∞

dk k

d−1

−

= C(d)2

−1



∞

dx x

−1

−x

= C(d)2

−1

(

)

where we changed integration variables and recognized the integral representation of the gamma function

(z +1) ≡



∞

dx x

−x

. (Recall that upon integration by parts we obtain (z +1) =z(z), so that (n) =(n −1)!

for n an integer.) Therefore C(d) =2π

d/2

/ (d/2) and



kF(k

) =

2π

d/2

(d/2)



∞

dk k

d−1

F(k

) (8)

Setting d =1 in (8) we determine (

) = π

, and setting F(k

) = δ(k − 1) we see that the area of the (d − 1)-

dimensional sphere is equal to C(d), thus recovering various results you learned in school about circles and

spheres: C(2) = 2π and C(3) =4π .

The new result you need as a budding field theorist is for d =4:



kF(k

) = π



∞

F(k

) (9)

So finally we have

I =

−i

16π



∞

+ m

)

−i

16π

(10)

We have derived the basic formula for doing Feynman integrals:



(2π)

− m

+ iε)

−i

32π

(11)

(With the telltale iε we have evidently moved back to Minkowski space.) As an exercise you can go through the

same steps to find





(2π)

− m

+ iε)

16π



log







− 1 +

...



(12)

Here a cutoff is needed, which we introduce by setting the upper limit in the integral over k

in the analog of

(10) to 

. As a check, differentiate (12) with respect to m

to recover (11). As another exercise show that





(2π)

− m

+ iε)

−i

16π





− 2m

log







+ m

...



(13)

In (12) and (13) (

...

) denote terms that vanish for 

m

. In some texts, the (−1) in (12) is dropped by absorbing

it into 

. But then we have to be careful to adjust (13) accordingly if it appears in the same calculation.

540 | Appendix D. Identities and Feynman Integrals

A useful identity in combining denominators is

...x

= (n − 1)!



...



dα

...dα

⎛

⎝

1 −



⎞

⎠

(α

+ α

...

+ α

)

(14)

For n = 2,



dα

[αx + (1 − α)y]

(15)

and for n = 3,

xyz

= 2



dαdβdγδ(α + β + γ − 1)

(αx + βy + γz)

(16)

= 2



triangle

dαdβ

[z + α(x − z) + β(y − z)]

where the integration region is the triangle in the α-β plane bounded by 0 ≤ β ≤1 − α and 0 ≤ α ≤ 1.

Appendix E Dotted and Undotted Indices and the Majorana Spinor

We develop the dotted and undotted notation introduced in chapter II.3 for further use in discussing supersym-

metry in chapter VIII.4 and in part N. In essence, the appearance of undotted and dotted indices can be traced

back to the fact that the algebra of the Lorentz group SO(3, 1), with the generators



J + i



K and



J − i



K, breaks

up into two pieces, each isomorphic to the algebra of SU(2). The absence or presence of the dot allows us to keep

track of which SU(2) we are talking about.

Here I will use extensively results from chapter II.3 and from the exercises (do them!) there without bothering

to write them down again here.

In the Weyl basis of chapter II.1



0 σ

¯σ



(1)

where σ

= (I , σ) and ¯σ

= (I , −σ). Knowing that γ

acts on

 =



¯χ

˙α



we see that σ

and ¯σ

carry indices as follows:

(σ

)

α ˙α

and ( ¯σ

)

˙αα

(2)

This is consistent with what you know: the Lorentz vector transforms like (

) and thus straddles the two

SU(2)’s. The matrices σ

and ¯σ

mix dotted and undotted indices. We will make good use of this observation

later.

Let us check that the Lorentz transformation property of the Dirac spinor  is consistent with what was

discussed in chapter II.1. There we learned that  →e

−

μν



μν

, where 

μν

≡

[γ

, γ

]. (We want to use the

symbol σ

μν

for some other quantity, hence the change of notation.) Using (1) we obtain



μν

= 2i



μν

0 ¯σ

μν



where σ

μν

≡

(σ

¯σ

−σ

¯σ

) and ¯σ

μν

≡

( ¯σ

−¯σ

). From (2) we see that these two matrices carry indices

as follows:

(σ

μν

)

and ( ¯σ

μν

)

˙α

(3)