Zee A. Quantum Field Theory in a Nutshell
Подождите немного. Документ загружается.

542 | Appendix E. Indices and the Majorana Spinor
Again, this reflects the fact that the antisymmetric tensor (such as the electromagnetic field F
μν
) transforms like
(1, 0) + (0, 1).
The matrices σ
μν
and ¯σ
μν
may seem alien, but recall that they are manufactured out of the familiar Pauli
matrices and so they are simply Pauli matrices (what else could they be?) themselves. In particular,
σ
0i
=−¯σ
0i
=−
1
2
σ
i
and σ
ij
=¯σ
ij
=−
i
2
ε
ij k
σ
k
Note that these relations are consistent with (σ
μν
)
†
=−( ¯σ
μν
), which in turn follows from (
μν
)
†
= γ
0
μν
γ
0
.
Mother Nature is kind to the students of quantum field theory. The relativistic spinor breaks up into two
2-component spinors acted on by the Pauli matrices. What you learned in nonrelativistic quantum mechanics
continues to be relevant here.
Thus under an infinitesimal Lorentz transformation
ψ
α
→
I +
1
2
ω
μν
σ
μν
β
α
ψ
β
(4)
and
¯χ
˙α
→
I +
1
2
ω
μν
¯σ
μν
˙α
˙
β
¯χ
˙
β
(5)
You should check that it all works out according to plan. Everything is consistent with what we learned in chapter
II.3, in particular, that boosts act oppositely on (
1
2
,0) and (0,
1
2
), but rotations act the same.
Thus far, on the spinor fields ψ
α
and ¯χ
˙α
, the dotted indices always live upstairs and the undotted indices
downstairs. What would get them to change floors? Charge conjugation.
Recall from chapter II.1 that the charge conjugated field is defined by
c
≡C
¯
T
[where T denotes transpose,
¯
means
†
γ
0
, and C
−1
γ
μ
C =−(γ
μ
)
T
.] In the Weyl basis, we can choose
C = ζγ
0
γ
2
= ζ
−σ
2
0
0 σ
2
(6)
The condition (
c
)
c
= implies |ζ |=1. We choose ζ =−i . Explicitly,
c
=
iσ
2
¯χ
∗
−iσ
2
ψ
∗
We now introduce some notation, the wisdom of which will soon become clear. Given ψ
α
and ¯χ
˙α
, define
¯
ψ
˙α
≡ (ψ
α
)
∗
and χ
α
≡ ( ¯χ
˙α
)
∗
(7)
Weird, complex conjugation puts on a dot and a bar.
We raise and lower undotted indices as follows: ψ
α
=ε
αβ
ψ
β
and ψ
β
=ε
βγ
ψ
γ
which implies that ε
αβ
ε
βγ
=δ
γ
α
.
Thus, if we choose
ε
αβ
=
01
−10
= (iσ
2
)
αβ
then
ε
βγ
=
0 −1
10
= (−iσ
2
)
βγ
We are forced to define ε
12
=+1 and ε
12
=−1 to have opposite signs, a fact to keep in mind.
You should realize by now that what we are doing can again be traced back to that peculiar fact about Pauli
matrices (appendix B):
(iσ
2
)σ
∗
i
(−iσ
2
) =−σ
i
(8)
or equivalently
σ
2
σ
T
i
σ
2
=−σ
i
(9)

Appendix E. Indices and the Majorana Spinor | 543
an identity in one guise or another familiar from quantum mechanics. We have used it again and again, in
appendix B and in the text (for example, in connection with Majorana masses and with the Higgs field). From
(8) we have (iσ
2
)σ
μ∗
(−iσ
2
) =¯σ
μ
and hence
(iσ
2
)(σ
μν
)
∗
(−iσ
2
) =¯σ
μν
(10)
Analogously, we raise and lower dotted indices as follows:
¯
ψ
˙α
= ε
˙α
˙
β
¯
ψ
˙
β
and
¯
ψ
˙
β
= ε
˙
β ˙γ
¯
ψ
˙γ
. Referring to (7) we
see that ε
˙α
˙
β
is numerically the same as ε
αβ
, and ε
˙
β ˙γ
is numerically the same as ε
βγ
.
You now see the rationale of these apparently capricious choices: we can now write
c
=
χ
α
¯
ψ
˙α
(11)
Referring to
=
ψ
α
¯χ
˙α
(12)
we see that the point of the notation is that ψ
α
and χ
α
transform in the same way and are the same kind of
creature (and similarly for ¯χ
˙α
and
¯
ψ
˙α
.)
We now come to the all-important concept of a Majorana spinor. Ettore Majorana, a brilliant physicist,
mysteriously disappeared early in his career. Fermi supposedly described Majorana as “a towering giant without
any common sense.”
1
Given a Dirac spinor ,if =
c
, then is said to be a Majorana spinor.
Comparing (12) and (11), we see that a Majorana spinor has the form
M
=
ψ
α
¯
ψ
˙α
(13)
An obvious remark but a handy mnemonic: Given a Weyl spinor ψ
α
we can construct a Majorana spinor, and
given two Weyl spinors we can construct a Dirac spinor: one Weyl equals one Majorana, and two Weyls equal
one Dirac.
Incidentally, another way of seeing that complex conjugation puts on a dot is that (see chapter II.3) conjugation
interchanges
J + i
K and
J − i
K.
The point to remember is simply that given a spinor λ
α
, then λ
˙α
transforms like (λ
α
)
∗
. You should verify this,
keeping in mind (10).
The utility of the notation is similar to that of the covariant and contravariant (or upper and lower) indices in
special and general relativity. We always contract an upper index with a lower index. Here we have the additional
rule that an undotted upper index can only be contracted with an undotted lower index, but never with a dotted
lower index, (obviously, since they belong to different algebras.) It is easy to verify these rules. For example, let
us show that η
α
ψ
α
is invariant. Using (4) we proceed with laboriously careful pedagogy:
η
α
→ η
α
= ε
αβ
η
β
= ε
αβ
(e
1
2
ωσ
)
γ
β
η
γ
= ε
αβ
(e
1
2
ωσ
)
γ
β
ε
γρ
η
ρ
= (e
−
1
2
ωσ
T
)
α
ρ
η
ρ
(14)
where we used once again the identity (9). Then η
α
ψ
α
→η(e
−
1
2
ωσ
T
)
T
(e
1
2
ωσ
)ψ =ηψ, which is indeed an invariant.
In special and general relativity we raise and lower indices with the metric, which is of course symmetric.
Here we raise and lower indices with the antisymmetric ε symbol and as a result signs pop up here and there.
For example, η
α
ψ
α
= ε
αβ
η
β
ψ
α
= η
β
(−ε
βα
)ψ
α
=−η
β
ψ
β
. Contrast this with the scalar product of two vectors
v
μ
w
μ
= v
μ
w
μ
. If we want to suppress indices and write ηψ, we must decide once and for all what that means.
The standard convention is to define
ηψ ≡ η
α
ψ
α
(15)
and not η
β
ψ
β
. This rule is sometimes stated by saying that in contracting undotted indices we always go from
the northwest to the southeast, and never from southeast to northwest. As we learned in chapter II.5, spinor
fields are to be treated as anticommuting Grassman variables under the path integral, so that −η
β
ψ
β
= ψ
β
η
β
.
We end up with the nice rule ηψ = ψη.
1
M. Gell-Mann, private communication. Incidentally, the name Ettore corresponds to Hector in English.

544 | Appendix E. Indices and the Majorana Spinor
Similarly, we define
¯χ
¯
ξ ≡¯χ
˙α
¯
ξ
˙α
=
¯
ξ ¯χ (16)
In contracting dotted indices we always go from southwest to northeast. Of course, none of this “Santa Barbara
to Cambridge” convention is needed if the indices are displayed explicitly.
Just as in special and general relativity, where the upper and lower indices are very useful in telling us
whether expressions we write down make sense, the undotted and dotted upper and lower indices allow us
to see immediately that ηψ and ησ
μν
ψ make sense, but that ησ
μ
ψ does not. [Look at (2) and (3) and notice the
kind of indices that appear.] The notation of course just codifies in a convenient way the group theory fact that
(
1
2
,0) ⊗ (
1
2
,0) = (0, 0) ⊕ (1, 0), namely, that out of two Weyl spinors we can make a scalar and a tensor but not
a vector.
As always, notation should be driven by physics and computational convenience (which is intimately con-
nected to elegance).
To gain familiarity with the dotted and undotted 2-component notation, you should work out some of the
identities in the exercises. These identities are useful when working with supersymmetric field theories.
Exercises
E.1 Show that ησ
μν
ψ =−ψσ
μν
η and ¯χ ¯σ
μ
ψ =−ψσ
μ
¯χ .
E.2 Show that (θϕ)( ¯χ
¯
ξ) =−
1
2
(θσ
μ
¯
ξ)(¯χ ¯σ
μ
ϕ).
E.3 Show that θ
α
θ
β
=
1
2
(θθ)δ
α
β
. [Hint: simply evaluate the two sides for all possible cases.]
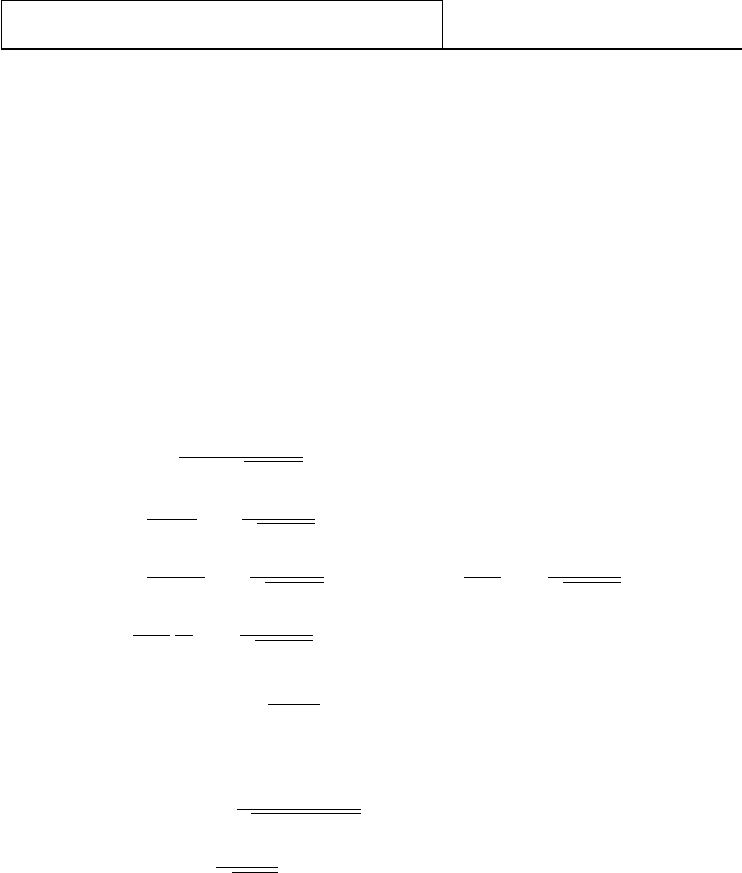
Solutions to Selected Exercises
Part I
I.3.1 From the text we have for x
0
= 0,
D(x) =−i
d
3
k
(2π)
3
2
k
2
+ m
2
e
−i
k
.
x
=−
i
2(2π)
2
∞
0
dkk
2
k
2
+ m
2
+1
−1
d(cos θ)e
−ikr cos θ
=−
1
2(2π)
2
r
∞
0
dkk
k
2
+ m
2
(e
ikr
− e
−ikr
) =−
1
8π
2
r
∞
−∞
dkk
k
2
+ m
2
e
ikr
=
i
8π
2
r
∂
∂r
∞
−∞
dk
k
2
+ m
2
e
ikr
The integrand in I ≡
∞
−∞
(dk/
k
2
+ m
2
)e
ikr
has a cut along the imaginary axis going from imto i∞(and
another cut we don’t care about.) So fold the contour around the cut and change variable to k = i(m +y):
I = 2
∞
0
dye
−(y+m)r
1
(y + m)
2
− m
2
= 2
∞
1
due
−mru
1
√
u
2
− 1
= 2
∞
0
dte
−mr cosh t
.
546 | Solutions to Selected Exercises
At this point you can look in a table and find that this is some Bessel function and read off the large r
behavior, but it is more stylish to press on and descend steeply: we obtain
D(x) =−
im
4π
2
r
∞
0
dt(cosh t)e
−mr cosh t
=−
im
4π
2
r
∞
0
d(sinh t)e
−mr cosh t
=−
im
4π
2
r
∞
0
dse
−mr
√
s
2
+1
−
im
4π
2
r
∞
0
dse
−mr(1+
1
2
s
2
)
=
−im
2
4π
2
(
π
2(mr)
3
)
1
2
e
−mr
,
using the Gaussian integral from the appendix of chapter I.2.
I.3.2 We evaluate
D(x) =
d
2
k
(2π)
2
e
ikx
k
2
− m
2
+ iε
by contours as in the text and obtain
D(x) =−i
dk
(2π)2ω
k
[e
−i(ω
k
t−kx)
θ(x
0
) + e
i(ω
k
t−kx)
θ(−x
0
)]
For x
0
= 0, we recognize the integral
D(x) =−i
+∞
−∞
dk
(2π)2
k
2
+ m
2
e
−ikx
as a Bessel function from exercise I.3.1:
D(x) =
−i
2π
K
0
(m|x|) →
−i
2π
π
2m|x|
e
−m|x|
with the expected exponential decay for large x.
I.7.2 Expanding and keeping only the desired terms
Z(J) →C
1 +
1
2!
−
i
4!
λ
2
d
4
w
1
d
4
w
2
δ
iδJ(w
1
)
4
δ
iδJ(w
2
)
4
1
6!
−
i
2
d
4
xd
4
yJ (x)D(x − y)J(y)
6
Just keep on differentiating.
I.7.4 Write k
1
=(
√
k
2
+ m
2
,0,0,k) and k
2
=(
√
k
2
+ m
2
,0,0,−k). Then E = 2
√
k
2
+ m
2
≥2m. Physically, a
pair of mesons can be produced when E ≥ 2m.
I.8.1 Do the k
0
integral on the left-hand side of (I.8.14):
dk
0
δ((k
0
)
2
− ω
2
k
)θ(k
0
)f (k
0
,
k), where ω
k
≡
+
k + m
2
. Using (I.2.12) and picking up the positive root because of the step function, we obtain
∞
0
dk
0
(δ(k
0
− ω
k
)/(2k
0
))f (k
0
,
k) = f(ω
k
,
k)/(2ω
k
).
To verify the invariance explicitly, boost in the x direction and drop the subscript on ω
k
: k
x
→
sinh φω+ cosh φk
x
and ω → cosh φω+sinh φk
x
. Then, using ω
2
= (k
x
)
2
+
...
and hence ωdω =
k
x
dk
x
, we have dk
x
→ (sinh φ(k
x
/ω) + cosh φ)dk
x
. Hence dk
x
/ω → dk
x
/ω.
Solutions to Selected Exercises | 547
I.8.2 Clearly, only the terms aa
†
and a
†
a in H contributes to <
k
|H |
k>. Extract these two types of terms in
d
D
xϕ(x)
2
=
d
D
x
d
D
q
(2π)
D
2ω
q
d
D
q
(2π)
D
2ω
q
[a(q)a
†
(q
)e
−i(ω
q
t−q
.
x)
e
i(ω
q
t−q
.
x)
+ h.c.]
=
d
D
q
2ω
q
[a(q)a
†
(q) + a
†
(q)a(q)]
and so H is for our purposes effectively equal to
d
D
q
ω
q
2
[a(q)a
†
(q) + a
†
(q) a(q)], which upon using
the commutation relation is equal to
d
D
q
ω
q
2
[δ
(D)
(
0) + 2a
†
(q)a(q)]. We recognize the first term as the
vacuum calculated in the text. Note that the definition of the delta function (2π)
D
δ
(D)
(
k) =
d
D
xe
i
k
.
x
implies δ
(D)
(
0) = [1/(2π)
D
]
d
D
x = V/(2π)
D
. Thus, subtracting off the vacuum energy, we have H
effectively equal to
d
D
qω
q
a
†
(q)a(q), which just says that a mode of momentum q carries energy ω
q
.
In particular, using the commutation relation twice we have <
k
|H |
k>= δ
(D)
(
k
−
k)ω
k
. The energy of
a particle of momentum
k is ω
k
relative to the vacuum.
I.8.4 Q =
d
D
xJ
0
(x) =
d
D
x(ϕ
†
i∂
0
ϕ − i(∂
0
ϕ
†
)ϕ). Focus on the first term:
d
D
x
d
D
k
(2π)
D
2ω
k
d
D
k
(2π)
D
2ω
k
[a
†
(
k
)e
i(ω
k
t−
k
.
x)
+ b(
k
)e
−i(ω
k
t−
k
.
x)
]ω
k
[a(
k)e
−i(ω
k
t−
k
.
x)
− b
†
(
k)e
i(ω
k
t−
k
.
x)
]
Note that i∂
0
brings down a factor of ω
k
and produces a relative sign between a and b
†
. As in exercise I.8.2
the integral over x produces a delta function that collapses the two k integrals into one, giving
d
D
k
1
2
(a
†
(
k)a(
k) −b(
k)b
†
(
k) −a
†
(−
k)b
†
(
k)e
2iω
k
t
+ b(−
k)a(
k)e
−2iω
k
t
)
The second term in −i(∂
0
ϕ
†
)ϕ in J
0
(x) is just the hermitean conjugate of the first term ϕ
†
i∂
0
ϕ. Thus,
adding the hermitean conjugate of what we have just obtained, we find
Q =
d
D
k[a
†
(
k)a(
k) −b(
k)b
†
(
k)]
=
d
D
k[a
†
(
k)a(
k) −b
†
(
k)b(
k)] +δ
(D)
(
0)
d
D
k
The infinite additive constant is to be subtracted out much like the vacuum energy. In some texts a normal
ordering operation, denoted by a pair of colons, is defined as follows: If you see : (
...
) : you are instructed
to move all the creation operators in the expression (
...
) to the left of the annihilation operators. In other
words, by fiat : b(
k)b
†
(
k) : ≡b
†
(
k)b(
k). The current is then defined by J
μ
(x) ≡ : (ϕ
†
i∂
μ
ϕ − i(∂
μ
ϕ
†
)ϕ) :.
Since the normal ordered current differs from the naively defined current by a c-number the most crucial
property of the current, namely current conservation ∂
μ
J
μ
= 0, is not affected. This is of course just a
formal way of saying that the value of the charge in the vacuum state is to be subtracted. In any case, the
result Q =
d
D
k[a
†
(
k)a(
k) − b
†
(
k)b(
k)] shows that a and b annihilate positive and negative charges,
respectively.
I.10.2 We have (repeated indices summed)
R
aa
R
bb
iD
a
b
(x) =
DϕR
aa
ϕ
a
(x)R
bb
ϕ
b
(0)e
iS
But we can change the integration variable from ϕ to Rϕ. Since the action S and the measure Dϕ are
both invariant under SO(N) rotations, this is equal to
Dϕϕ
a
(x)ϕ
b
(0)e
iS
= iD
ab
(x). Thus, we obtain
D
ab
=R
aa
R
bb
D
a
b
. The properties of the rotation group are such that the only solution of this equation
is D
ab
proportional to δ
ab
.

548 | Solutions to Selected Exercises
I.10.3 The field ϕ transforms as a symmetric traceless tensor (see appendix B) under SO(3), that is, with all
indices displayed, ϕ
ab
→ R
aa
R
bb
ϕ
a
b
= R
aa
ϕ
a
b
R
T
b
b
= (RϕR
T
)
ab
. As suggested in the hint, writing ϕ
as a 3 by 3 symmetric traceless matrix we have ϕ → RϕR
T
and thus the invariants are (up to quartic
order in ϕ) tr(∂
μ
ϕ)
2
,trϕ
2
,trϕ
4
, and (tr ϕ
2
)
2
. Remarkably, you can prove that tr ϕ
4
and (tr ϕ
2
)
2
actually
amount to only one invariant by diagonalizing
ϕ =
⎛
⎜
⎜
⎝
α 00
0 β 0
00−(α + β)
⎞
⎟
⎟
⎠
You can see by computation tr ϕ
4
and (tr ϕ
2
)
2
are both proportional to [α
2
+ β
2
+ (α + β)
2
]
2
. Thus, if
we restrict ourselves to quartic terms the Lagrangian L =
1
2
tr(∂
μ
ϕ)
2
−
1
2
m
2
tr ϕ
2
−λ(tr ϕ
2
)
2
actually has
an SO(5) symmetry (since ϕ has 5 components.) This is an example of what is known as “accidental
symmetry.” Convince yourself that this holds only to quartic order in ϕ.
I.11.2 Varying g
μρ
g
ρλ
= δ
μ
λ
we have (δg
μρ
)g
ρλ
=−g
μρ
(δg
ρλ
), which upon multiplication by g
λν
becomes
δg
μν
=−g
μρ
(δg
ρλ
)g
λν
. You may recognize this as just the statement δM
−1
=−M
−1
(δM)M
−1
for a
matrix M . To evaluate δg we use the important identity det M = e
Tr log M
, which you can prove easily
by diagonalizing M with a similarity transformation. The left hand side is equal to the product of the
eigenvalues of M , while the right hand side is equal to the exponential of the sum of logarithms of the
eigenvalues. {You can define the logarithm of a matrix by expanding log[I + (M −I)] in a power series
in (M −I).}
Thus, δ det M =(det M) tr M
−1
δM and so δg = gg
νμ
δg
μν
. We are now ready to vary
S =
d
4
x
√
−g
1
2
(g
μν
∂
μ
ϕ∂
ν
ϕ − m
2
ϕ
2
) ≡
d
4
x
√
−gL
Plugging in, we have
δS =
d
4
x
√
−g[
1
2
g
νμ
δg
μν
L−g
μρ
(δg
ρλ
)g
λν
1
2
∂
μ
ϕ∂
ν
ϕ]
Thus,
T
μν
=−
2
√
−g
δS
δg
μν
= g
μρ
g
νλ
∂
ρ
ϕ∂
λ
ϕ − g
μν
L
In the flat spacetime limit
T
00
= (∂
0
ϕ)
2
− L =
1
2
((∂
0
ϕ)
2
+ (
∇ϕ)
2
+ m
2
ϕ
2
)
precisely the energy density as promised.
I.11.3 Using the expression for T
μν
from the preceding exercise, we have
P
i
=
d
3
xT
0i
=−
d
3
x∂
0
ϕ∂
i
ϕ
and
[P
i
, ϕ(x)] =−
d
3
y[∂
0
ϕ(y), ϕ(x)]∂
i
ϕ(y) = i∂
i
ϕ(x)
Thus, combined with the fact that P
0
= H , we have [P
μ
, ϕ(x)] =−i∂
μ
ϕ(x), which just reflects the fact
that P
μ
and x
ν
are conjugate variables.
I.11.4 Evaluating T
μν
=−F
μλ
F
λ
ν
− η
μν
L, we have
T
ij
=−F
iλ
F
λ
j
+
1
2
δ
ij
(
E
2
−
B
2
) =−E
i
E
j
+ F
ik
F
jk
+
1
2
δ
ij
(
E
2
−
B
2
)
Solutions to Selected Exercises | 549
Since F
ik
F
jk
=ε
ikm
ε
jkn
B
m
B
n
=δ
ij
B
2
−B
i
B
j
, we obtain the announced result. Note that δ
ij
T
ij
=
1
2
(
E
2
+
B
2
) = T
00
and hence T =0.
Part II
II.1.1 Continuing the hint, we have
δ(
¯
ψγ
μ
γ
5
ψ) =
¯
ψ
i
4
ω
λρ
[σ
λρ
, γ
μ
γ
5
]ψ =
¯
ψ
i
4
ω
λρ
[σ
λρ
, γ
μ
]γ
5
ψ
since γ
5
anticommutes with gamma matrices and hence commutes with the product of two gamma
matrices. Inserting [σ
λρ
, γ
μ
] as given in the text we have δ(
¯
ψγ
μ
γ
5
ψ) = ω
μ
λ
¯
ψγ
λ
γ
5
ψ , which is precisely
how a vector transforms. Under parity
¯
ψγ
μ
γ
5
ψ →
¯
ψγ
0
γ
μ
γ
5
γ
0
ψ which equals
¯
ψγ
5
γ
0
ψ =−
¯
ψγ
0
γ
5
ψ
for μ = 0, and
¯
ψγ
0
γ
i
γ
5
γ
0
ψ =
¯
ψγ
i
γ
5
ψ for μ = i. The time component flips sign while the spatial
components do not. Thus, the behavior under parity is opposite to that of a normal vector:
¯
ψγ
μ
γ
5
ψ
is an axial vector. The other cases proceed similarly.
II.1.2 From ψ
L
=
1
2
(1 −γ
5
)ψ and ψ
R
=
1
2
(1 +γ
5
)ψ , we find
¯
ψ
L
=ψ
†
L
γ
0
=ψ
†
1
2
(1 −γ
5
)γ
0
=
¯
ψ
1
2
(1 +γ
5
) and
¯
ψ
R
=
¯
ψ
1
2
(1 −γ
5
). We then just use the properties of P
L
and P
R
repeatedly. For example,
¯
ψ
L
ψ
R
=
¯
ψ
1
2
(1 +
γ
5
)ψ and
¯
ψ
R
ψ
L
=
¯
ψ
1
2
(1 −γ
5
)ψ , or equivalently,
¯
ψψ =
¯
ψ
L
ψ
R
+
¯
ψ
R
ψ
L
and
¯
ψγ
5
ψ =
¯
ψ
L
ψ
R
−
¯
ψ
R
ψ
L
.As
another example,
¯
ψ
L
γ
μ
ψ
L
=
¯
ψ
1
2
(1 + γ
5
)γ
μ
1
2
(1 − γ
5
)ψ =
¯
ψγ
μ
1
2
(1 − γ
5
)ψ and
¯
ψ
R
γ
μ
ψ
R
=
¯
ψγ
μ
1
2
(1 +
γ
5
)ψ . Note that various combinations vanish, for example,
¯
ψ
L
ψ
L
=0,
¯
ψ
L
γ
μ
ψ
R
=0, and so on. Complete
the exercise.
II.1.3–4 In the appropriate basis the Dirac equation becomes
E − mpσ
3
−pσ
3
−E − m
φ
χ
= 0
that is, (E − m)φ + pσ
3
χ = 0 and −pσ
3
φ − (E + m)χ = 0. The second equation informs us that χ =
−[p/(E + m)]σ
3
φ. For a slow electron χ −(p/2m)σ
3
φ, so that χ is smaller than φ by the factor p/2m.
The first equation then reduces to (E −m −p
2
/2m)φ = 0, which just reminds us of the relation between
energy and momentum in the nonrelativistic limit.
II.1.5 In the Weyl basis the Dirac equation for a relativistic electron moving along the 3-axis E(γ
0
−γ
3
)ψ =0
becomes
0 I − σ
3
I + σ
3
0
ψ
L
ψ
R
= 0
Since
σ
12
≡
i
2
[γ
1
, γ
2
] =−
i
2
[σ
1
, σ
2
] ⊗I = σ
3
⊗ I =
σ
3
0
0 σ
3
under a rotation around the 3-axis, ψ
L
→ e
−(i/4)ωσ
3
ψ
L
= e
+(i/4)ω
ψ
L
while ψ
R
→ e
−(i/4)ωσ
3
ψ
R
=
e
−(i/4)ω
ψ
R
. Indeed, the left and right handed fields rotate in opposite directions.
II.1.6 In the Weyl basis, the Dirac equation γ
.
pu = 0 becomes σ
μ
p
μ
η = 0, and ¯σ
μ
p
μ
χ =0, with
u =
χ
η
The solutions are
η =
p
1
− ip
2
p
0
− p
3
and η =
p
0
+ p
3
p
1
+ ip
2
550 | Solutions to Selected Exercises
for the two possible helicities. The corresponding solutions for χ may be obtained by p ↔−p. We have
¯uu = p
.
p = 0. For a particle moving in the +3 direction, η = 0 and
χ =2E
0
1
and
η = 2E
1
0
and χ = 0. The Lorentz vector ¯uγ
μ
u = (2E)
2
(1, 0, 0, 1). (What other direction could it point in?) For
a particle moving in the −3 direction, η and χ exchange roles. This exercise shows explicitly that for
massless particles we can use 2-component spinors. (What happens if parity is broken?)
II.1.8 In either the Dirac or the Weyl basis, (ψ
c
)
c
= γ
2
(γ
2
ψ
∗
)
∗
= ψ .
II.1.9 It is easiest to work in either the Dirac or the Weyl basis. Let ψ be left handed, that is (1 + γ
5
)ψ =0.
Then (1 − γ
5
)ψ
c
= (1 − γ
5
)γ
2
ψ
∗
= γ
2
(1 + γ
5
)ψ
∗
= 0 since γ
5
is real.
II.1.10 ψCψ → ψe
−
i
4
ω
λρ
(σ
λρ
)
T
Ce
−
i
4
ω
μν
σ
μν
ψ =ψCψ since (σ
λρ
)
T
C =−Cσ
λρ
.
II.1.12 Under parity or reflection in a mirror, x
1
→x
1
and x
2
→−x
2
. Choose γ
0
=σ
3
, γ
0
γ
1
=σ
1
, and γ
0
γ
2
=
σ
2
. Multiply the Dirac equation (iγ
μ
∂
μ
− m)ψ =0byγ
0
and write [i(∂
0
+ γ
0
γ
i
∂
i
) − γ
0
m]ψ =0. Then
multiplying by σ
1
reverses the sign of the ∂
2
term, but also the mass term. I leave it to you to discuss
time reversal.
II.2.1 Apply Noether for the transformation
ψ →e
iθ
ψ =(1 +iθ)ψ
Then
δL
δ(∂
μ
ψ)
δψ +
δL
δ(∂
μ
¯
ψ)
δ
¯
ψ =
¯
ψiγ
μ
(iθψ)
Note that formally L does not depend on ∂
μ
¯
ψ. Thus, up to overall factors we can choose J
μ
=
¯
ψγ
μ
ψ
with the corresponding charge Q =
d
3
x
¯
ψγ
0
ψ into which we plug (II.2.10)
ψ(x) =
d
3
p
(2π)
3/2
(E
p
/m)
1/2
s
[b(p, s)u(p, s)e
−ipx
+ d
†
(p, s)v(p, s)e
ipx
]
At this point, the calculation pretty much parallels what you did in exercise I.8.4. The integration
d
3
x
over space produces a delta function that sets the momentum variables in ψ and in
¯
ψ equal to one
another. The new feature here is that we encounter objects such as ¯uγ
0
u. Invoking Lorentz invariance and
referring to the rest frame form of u and v we have ¯u(p, s)γ
μ
u(p, s
) =δ
ss
p
μ
/m, ¯u(p, s)γ
μ
v(p, s
) =0,
and so on. We obtain
Q =
d
3
p
(2π)
3
(E
p
/m)
s
[b
†
(p, s)b(p, s) + d(p, s)d
†
(p, s)]
As in exercise I.8.4 we have to move the creation operator d
†
to the left of the annihilation operator d
and subtract off an infinite constant. Thus, finally
Q =
d
3
p
(2π)
3
(E
p
/m)
s
[b
†
(p, s)b(p, s) − d
†
(p, s)d(p, s)]
showing clearly that b annihilates a negative charge and d a positive charge.
Solutions to Selected Exercises | 551
To calculate [Q, ψ(0)] =
d
3
x[
¯
ψ(x)γ
0
ψ(x), ψ(0)] we use the identity [AB , C] = A{B , C}−{A, C}B
and the canonical anticommutation relation (II.2.4). We find [Q, ψ(0)] =−ψ(0), thus showing that b
and d
†
must carry the same charge.
II.3.4 The desired equations are γ
μ
αμ
= 0 (this takes out 4 components since α takes on 4 values) and
(p − m)
β
α
βμ
= 0 (for each μ this takes out 2 components and so altogether 4 × 2 = 8 components.)
Thus, 16 − 4 − 8 =4 components as desired. Another way of saying this is that γ
μ
αμ
is a Dirac spinor
and hence the spin
1
2
part of the vector-spinor
αμ
.
II.6.4 It is good practice to be as symmetrical as one can in calculations. So define p
3
≡−P
1
and p
4
≡−P
2
and
add the 6 (not 3) combinations appearing in the definitions of s, t, and u, thus obtaining
2(s + t +u) = (p
1
+ p
2
)
2
+ (p
3
+ p
4
)
2
+ (p
3
+ p
1
)
2
+ (p
4
+ p
2
)
2
+ (p
4
+ p
1
)
2
+ (p
3
+ p
2
)
2
= 3
4
i=1
m
2
i
+ 2(p
1
.
p
2
+ p
3
.
p
4
+ p
1
.
p
3
+ p
2
.
p
4
+ p
1
.
p
4
+ p
2
.
p
3
)
The second group of terms on the right-hand side collect into (
4
i=1
p
i
)
2
−
4
i=1
m
2
i
. (Obviously, we
have for convenience changed notation slightly, setting m
3
= M
1
and m
4
= M
2
.)
II.6.5 Referring to (C.11) we see that in dσ the factor
1
|v
1
−v
2
|E(p
1
)E(p
2
)
1
(2π)
3
E(k
1
)
...
1
(2π)
3
E(k
n
)
(2π)
4
reduces to
1
2
(m/E)
4
[1/(2π)
2
]. Integrating the factor d
3
P
1
d
3
P
2
δ
(4)
(p
1
+p
2
−P
1
−P
2
) over
P
2
we knock
off 3 of the delta functions, leaving us with ddP
1
P
2
1
δ(2E − E
1
), and so the integral over P
1
gives d
1
2
E
2
.
Finally, the factor containing the “real physics” is
1
2
s
S
|M|
2
= (e
4
/4m
4
)f (θ). Multiplying the three
factors together and dividing by d, we obtain dσ /d = (
1
2
)
5
[e
4
/(2π)
2
](1/E
2
)f (θ), as given in the text.
Note that m cancels out as expected. We should be able to take the limit m →0 compared to the energies
without the cross section either blowing up or vanishing.
II.6.7
=
|M|
2
2M
d
3
k
(2π)
3
2ω
d
3
k
(2π)
3
2ω
(2π)
4
δ
4
(k + k
− q)
Knock off the
k
integral and do the angular part of the
k integral to obtain
=
|M|
2
8πM
dkk
2
ωω
δ(
k
2
+ m
2
+
k
2
+ m
2
− M)
Using (I.2.12), we evaluate the integral as (k
2
/ωω
)(1/(
k
ω
+
k
ω
)) =k/M. Solving
√
k
2
+ m
2
+
√
k
2
+ m
2
=
M for k we obtain the stated result.
Part III
III.1.2 The amplitude should become nonanalytic when both denominators of the integrand
(k
2
− m
2
+ iε)((K −k)
2
− m
2
+ iε)
vanish, namely when k
2
= m
2
and (K −k)
2
= m
2
. But we found the condition in exercise I.7.4, namely
that K
2
≥ 4m
2
. Referring to (III.1.14)
M =
iλ
2
32π
2
1
0
dα log
2
α(1 − α)K
2
− m
2
+ iε
we see that the log has a cut starting at K
2
=m
2
/α(1 − α).Asα ranges from 0 to 1, the minimum value
of m
2
/α(1 − α) is attained at α =
1
2
. So indeed, the cut starts at K
2
= 4m
2
.
