Zee A. Quantum Field Theory in a Nutshell

Подождите немного. Документ загружается.

482 | Part N

This treatment of the black hole as a point particle is only valid for ωr

1of course. The

(

...

) in iM represents diagrams we have not included, for example, the one originating

from the first term in (4) (namely the term responsible for keeping us down to earth!). A

nice feature of the argument I am about to give is that we don’t even need to know what

the terms in (

...

) are.

On the other hand, we argue that by dimensional analysis the cross section must have

the form σ(ω)= r

f(ωr

) since the only length scale in the Schwarzschild metric is r

Expanding the unknown function f(ωr

) in powers of its argument we have σ(ω) =

...

+ αω

...

with α some constant. (A technical aside: the massless graviton could

produce infrared factors like log ωr

, which we ignore for our purposes.)

Requiring that the two expressions agree, we obtain c

E,B

∼ M

. Indeed, as expected,

the couplings c

E,B

are highly suppressed as r

→ 0.

Exercise

N.1.1 Using considerations similar to those in the text, show that the scattering cross section for a photon of

frequency ω on an atom or a molecule vanishes like ω

as ω →0, a result which, as mentioned in chapter

VIII.3, underlies the well-known explanation of why the sky is blue.

N.2 Gluon Scattering in Pure Yang-Mills Theory

Boil and toil with Feynman diagrams

You might think that after some 50 years, there could not possibly be any novelty in

calculating Feynman amplitudes. But you would be wrong. Over the last dozen years or so,

and largely since the first edition of this text, a group of intrepid searchers have found some

amazingly powerful methods of tackling Feynman diagrams. As I said at the beginning of

chapters VIII.4 and 5, I can only give you an introduction to this subject, telling you just

enough for you to explore this fast-growing literature.

To best appreciate this new development, you should do a little calculation before reading

further. Consider pure Yang-Mills theory, by consensus the nicest field theory we have,

simple to write down and perfumed with symmetries. Not even any fermions around to

mess things up. Call the gauge bosons gluons for convenience. Now calculate 5-gluon

scattering at tree level as shown in figure N.2.1. No loops, just trees. The Feynman rules

are given in chapter VII.1 and also in appendix C.

You really must calculate before reading on. I will wait for you. You think to yourself,

this is easy, just a bunch of tree diagrams. In fact, to make it easier, put all the external

gluons on-shell, that is, set p

= 0, i = 1, 2,

...

,5.

This calculation is not merely an idle exercise, but is in fact phenomenologically im-

portant. At an accelerator such as the soon-to-be-operational Large Hadron Collider, two

⫹ ⫹

⫹...

Figure N.2.1

484 | Part N

Result of a brute force calculation (actually only a small part of it):

⭈ k

␧

⭈ k

␧

⭈ ␧

␧

⭈ ␧

Figure N.2.2

protons are smashed together at high energies. Two gluons, one from each proton, collide

and produce three gluons, which then materialize into three jets of hadrons. Because of

asymptotic freedom, at high energies the effective coupling g becomes small enough for

perturbative field theory to be relevant, and the tree amplitude you are busily calculating

provides a key ingredient for the phenomenological models used to study the experimental

measurements.

Time’s up! A small part of the answer is shown in figure N.2.2, taken from a lecture by

Zvi Bern.

You really should take a look in order to appreciate, to be grateful for even, the

formalism to be explained in this chapter. You know that the amplitude is linear in each

of the five polarization vectors 

. The 3-gluon vertex (VII.1.11) is linear in momentum

and there are three of them in a typical diagram. Thus a typical term in the numerator

of the Feynman amplitude would be, as shown in the figure, p



rough estimate shows that there are almost 10,000 such terms. That’s why, in spite of my

admonition, you didn’t finish the calculation before reading ahead. Incidentally, you could

see that even 4-gluon scattering at tree level, though doable by hand, is rather involved.

Z. Bern, “Magic Tricks for Scattering Amplitudes,” http://online.itp.ucsb.edu/online/colloq/bern1/pdf/

Bern1.pdf.

N.2. Gluon Scattering | 485

New technology for Feynman diagrams

In practice, phenomenologists studying jet production have developed elaborate computer

codes based on numerical recursion and these prove to be quite efficient. In this introduc-

tory text, however, we are not after numerical efficiency but a deeper understanding of the

structure of multi-gluon amplitudes. I have set you up so that, surely, after your abortive

attempt to calculate the 5-gluon amplitude you now fully appreciate the need for new ways

of approaching Feynman diagrams. I will now explain some of the novel methods people

have invented over the last 15 years or so.

A relatively simple first step is to strip the color off the amplitude. Evidently, it is much

better to use the matrix notation of (IV.5.16) than the index notation of (IV.5.17). Instead

of the structure constants f

abc

and their products in the “indexed” Feynman rules in

(VII.1.11–13) we have colored Feynman rules (read appendix 1 now) with objects like

tr(T

, T

]) and tr([T

, T

][T

, T

]) for the cubic and quartic coupling vertex, respec-

tively, where T

denotes the matrix representing the suitably normalized generators of the

gauge group. Denote the color matrices carried by the external gluons by T

, T

...

(with n = 5 in the example you failed to do).

In calculating a multi-gluon scattering amplitude in tree approximation, you would find

each term multiplied by the product of a bunch of color traces, such as tr(T

A)tr(T

where A and B denote products of T ’s. Here the index e is carried by a virtual gluon and

hence is summed over. We now use the group theoretic identity (with e summed over) for

the gauge group SU (N) [recall (IV.5.19)]

)



−



(1)

(Here e =1,

...

, N

−1 and the indices i , j , k, l = 1,

...

, N , of course.) The second term

takes care of the traceless condition tr T

=0. However, we can drop it, since if we extend

the gauge group to U(N), that extra gluon does not couple to the other gluons anyway. Thus

tr(T

A)tr(T

B) =

tr(AB). Repeating this procedure, we reduce the product of traces to

a single trace of nT

’s multiplied together in some specific order.

Indeed, the astute reader will have noted that had we used the double-line formalism of

figure IV.5.2, this entire discussion would not even have been necessary. As we also saw

in chapter VII.4, the double-line formalism does offer many advantages.

The other simplifying step is to specify the helicity of the gluon instead of writing

the amplitude in terms of polarization vectors. You recall, from way back when, that a

massless spin 1 particle moving along the third-direction k = ω(1, 0, 0, 1) can have helicity

h =+, corresponding to the polarization vector  = 1/(

√

2)(0, 1, i,0), or helicity h =−,

corresponding to the polarization vector  = (1/

√

2)(0, 1, −i,0). We specify the external

gluons by momentum, helicity, and color: (p

, h

, a

, p

, h

, a

...

, p

, h

, a

Thus we can write the n-gluon amplitude as

M = i



permutations

tr(T

...

)A(1, 2,

...

, n) (2)

486 | Part N

Following the literature, we have compressed the notation further and denote {p

, h

}by i.

The sum is over all possible permutations of the n gluons. We can now focus on the “color

stripped” amplitude A(1, 2,

...

, n).

First, a triviality. It is convenient to treat the gluons as all outgoing (or if you prefer, as

all incoming), so that



=0 and the time component of some of the momenta can be

negative. We can then obtain the physically desired amplitude by crossing. Keep in mind

that under crossing p →−p and  → 

∗

, that is, the helicity flips.

The spinor helicity formalism

Now we are ready to return to the expression in figure N.2.2. The technical term for this

expression is an “unholy mess.” It turns out that the key to unraveling this hopeless morass

can be found in exercise II.3.1: that the Lorentz vector sits in the representation (

) and

thus can be constructed as a product of two spinors, one from the representation (

,0),

the other from (0,

). You did the exercise, didn’t you? So you know how to write, for

example, the momentum vector p

as a product of two spinors. To go on, you should also

read appendices B and E.

I am now ready to explain the spinor helicity formalism designed to exploit this peculiar

property of the Lorentz vector. Or, to say it a bit more mysteriously, I am going to show

you how to take the square root of the momentum.

Now you appreciate the power of the undotted-dotted notation introduced in appendix E.

The undotted index goes with (

,0), and the dotted with (0,

). We are looking for an object

transforming like (

,0) ⊗ (0,

) to represent a vector. The problem can then be stated as

follows: instead of writing momentum as p

, we want to write it as p

α ˙α

, an object carrying

an undotted and a dotted index, namelya2by2matrix in cruder language.

We merely have to flip through appendix E and look for an object carrying the desired

indices. There it is, (σ

)

α ˙α

, and indeed, its μ index is begging to be contracted with p

Thus, with no further work, we can write [since σ

= (I , σ)]

α ˙α

≡ p

(σ

)

α ˙α

= (p

I − p

)

α ˙α



− p

) −(p

− ip

)

−(p

+ ip

)(p

+ p

)



α ˙α

(3)

We have succeeded in writing the momentum asa2by2matrix. You may recognize this

as nothing but the matrix X

(with some trivial change in notation) used in appendix B

to construct the covering of SO(3, 1) by SL(2, C).

Given two vectors p and q, their scalar product is given by

q = ε

αβ

˙α

α ˙α

(4)

which you can check explicitly, writing the right-hand side as a trace and once again using

=−σ

, as we did in appendix E. For q =p, this reduces to p

p = ε

αβ

˙α

α ˙α

det p; here we recognized a definition of the determinant. [Of course, you could also eval-

uate the determinant of (3) by inspection, or recall that this was also used in appendix B.]

N.2. Gluon Scattering | 487

Clearly, there is an unavoidable notational overload: the single letter p denotes both the

vector and the matrix, but you should be able to tell from the context which object is being

referred to.

Here we are going to apply this formalism to massless gluons with lightlike momenta.

Things simplify considerably: for p lightlike, det p = 0 and thus the matrix p generically

has one 0 eigenvalue. (In fancy talk, the matrix has rank 1 rather than 2.) From elementary

linear algebra we recall thata2by2matrix m of rank 1 can always be written as m

with v and w two 2-component vectors, (obviously since the vector orthogonal to w provides

the 0 eigenvector.) Thus, for a lightlike vector, we can write

α ˙α

= λ

˙α

(5)

in terms of two 2-component spinors λ and

λ.

For physical momentum, the components p

are real, of course. I invite you to verify,

however, that everything we just did from (3) to (5) goes through even if p

are complex.

It turns out that in the next chapters we will find it convenient to consider complex

momentum.

Upon first exposure, the formalism appears quite opaque, but actually, like a lot of

formalisms, it is fairly simple or perhaps even trivial. If you are confused at any point in

the following exposition, just work things out explicitly. For example, consider a physical

momentum with p

= E>0. With no loss of generality, you can choose p to point along

the third direction, so that (with a trivial abuse of notation p =|p|)

p =



E − p 0

0 E + p



which for p lightlike collapses to the rank 1 matrix

p = 2E





= 2E





(

)

Thus, in this case, λ and

λ are both equal to

√





numerically. (To make sure you get it, work this out for p pointing in some other direction.)

You can think of the Pauli spinors λ and

λ as the “square root” of the Lorentz vector p

Note how the group theory discussion in chapter II.3 foreordained this rather nontrivial

possibility. After all, there we saw how a Lorentz vector can be constructed out of two Dirac

spinors u and u



Interestingly, in discussing ferromagnets and antiferromagnets in chapter VI.5, we used

a poor man’s version of (3), namely n = z

†

σz.

You learned in school that the ordinary square root has a sign ambiguity. Analogously,

in (5) p does not determine λ and

λ uniquely. We can always rescale λ → uλ and

λ →

for any complex number u. (You might have wondered what fixed the overall constant in

λ and

λ in the simple example above: I made an arbitrary choice.)

488 | Part N

For real momentum, the matrix p

α ˙α

(σ

)

α ˙α

is hermitean, which implies that

λ =λ

∗

is the complex conjugate of λ. The spinor

λ is not independent of λ, and so the rescaling

parameter u is restricted to be a phase factor e

iγ

. [Also, recall from appendix B how X

transforms under SL(2, C) and you will see that it is all consistent.] In this case, the

condition that p has rank 1 allows for two solutions: p

α ˙α

=±λ

˙α

, with the two possible

signs corresponding to whether p

> 0 or not.

A side remark at this point: We will see that it is useful to consider the group SO(2, 2)

instead of the Lorentz group SO(3, 1). Thus, as the discussion in appendix B indicates,

you can also take the square root of an SO(2, 2) vector and write p

α ˙α

= λ

˙α

, but with λ

and

λ two independent real spinors, as is consistent with the local isomorphism between

SO(2, 2) and SL(2, R) ⊗ SL(2, R). The rescaling mentioned above is now restricted to u

being a real number.

It is instructive to count the number of real degrees of freedom for these different

cases. A complex lightlike momentum depends on 4 × 2 − 2 = 6 real numbers, since the

condition p

now amounts to two real conditions, while λ and

λ each contains 2 complex

numbers, but with rescaling we are left with 2 × 2 − 1 = 3 complex numbers, that is, 6

real numbers. A real lightlike momentum depends on 4 − 1 = 3 real numbers, but now

λ is tied to λ containing 2 complex numbers, which get reduced to 3 real numbers after

rescaling by a phase factor. For a (real) lightlike vector transforming under SO(2, 2),we

have 2 real spinors, which after rescaling contains 3 real numbers. So it all works out, of

course.

I mention all this here for future use. It should be evident to you, for the rest of

this chapter, which statements hold for complex momenta and which hold only for real

momenta. At the end of the day, when we arrive at a physical quantity, such as the

amplitude, we will of course set the momenta contained therein to be real.

For two lightlike vectors p and q, write p

α ˙α

= λ

˙α

and q

α ˙α

= μ

˜μ

˙α

, then we have

q = (ε

αβ

)(ε

˙α

˜μ

) ≡λ, μ[

λ, ˜μ] (6)

Here we have defined the two Lorentz invariants

λ, μ≡ε

αβ

=−μ, λ (7)

and

[

λ, ˜μ] ≡ ε

˙α

˜μ

=−[ ˜μ,

λ] (8)

(treating the spinors as c-number objects.) Note in passing that with our convention,

= λ

and λ

=−λ

, and so λ, μ=−λ

+ λ

=−ε

αβ

We have already verified in (E.13) that λ, μ is invariant, but for the sake of total

pedagogical clarity let us check it once more, this time using infinitesimal transformations.

Write (E.4) more compactly as δλ

= σ

, where σ denotes some linear combination

of Pauli matrices. Noting that λ, μ is nothing but λσ

μ up to some irrelevant overall

constant, we have indeed δ(λσ

μ) = (λσ

μ + λσ

σμ) =0.

A notational remark: the twiddles in [

λ, ˜μ] are redundant. The square bracket is defined

only for spinors transforming like (0,

). Henceforth, we will write [λ, μ] ≡ ε

˙α

˜μ

N.2. Gluon Scattering | 489

For real physical momenta,

λ = λ

∗

so that λ, μ=[λ, μ]

∗

. Then p

q =λ, μ[λ, μ]

implies that λ, μ=

√

iφ

and [λ, μ] =

√

−iφ

, with some phase factor e

iφ

.We

thus conclude that the two spinorial products may be regarded as the (two) square roots

of the Lorentz dot product p

q up to a phase factor.

You could now raise an interesting question: how do we write the polarization vectors

(p) of a massless gluon?

The requirement that (p)

p = 0 can be satisfied, according to (4), by setting 

α ˙α

−1

˜μ

˙α

, for an arbitrary ˜μ

˙α

and with the factor d determined as follows. We require that,

for an arbitrary complex number w, scaling ˜μ →w ˜μ does not change  (since ˜μ is arbitrary

after all). Thus d has to be linear in ˜μ. The further requirement that d be Lorentz invariant

implies, as we just learned, that d =[x, μ], where ˜x is some (0,

) spinor. The only spinor

available is

λ and hence we obtain



−

α ˙α

˜μ

˙α

[λ, μ]

(9)

By convention, we will call this polarization negative helicity.

The arbitrary choice of ˜μ

˙α

represents the freedom inherent in a gauge theory. Indeed,

we see that gauge transformation corresponds to the spinorial shift ˜μ →˜μ +y

λ (for some

arbitrary number y) under which 

α ˙α

→

α ˙α

+yλ

˙α

, which translates into the usual shift

of  by some multiple of p.

The positive helicity polarization is given by the other possible choice



α ˙α

˙α

μ, λ

(10)

Check that it works. Gauge transformation now corresponds to the shift μ → μ +yλ. Note

that the polarization vectors are normalized as 



−

=μλ[μλ]/(μλ[μλ]) = 1.

Taming the unholy mess

Consider the tree-level scattering amplitude with n ≥ 4 outgoing massless gluons. (In this

and the next sections, we can take all momenta to be real.) The color-stripped amplitude

is then characterized by a string of helicities (h

,...,h

). Take for example the amplitude

with (+++

...

++). Upon crossing, it describes two gluons, each with helicity −, going

into n − 2 gluons all with helicity +. Both incoming gluons flip their helicity and thus

this amplitude is said to be maximal helicity violating. Your intuition may tell you that

this amplitude ought to be suppressed, since highly energetic massless particles tend to

maintain their helicities. If you try to verify this using traditional Feynman diagrams, you

would once again encounter a big mess.

The spinor helicity formalism rides to the rescue. Consider the amplitude A(h

...

, h

For each of the n gluons, we have p

iα ˙α

= λ

iα

i ˙α

, and an arbitrary spinor that we are

free to choose (subject to some conditions), namely either μ

iα

or ˜μ

i ˙α

, depending on

whether the corresponding helicity is + or −, respectively. There are quite a few indices,

but fortunately, in computing amplitudes, we encounter only Lorentz invariants, such as

490 | Part N



=ε

αβ

˙α



iα ˙α



jβ

(be sure to distinguish between the two varieties of epsilon here!),

and thus the spinor indices will be contracted over and disappear. In particular, we have

(omitting the comma in the angled and square brackets)



μ

[λ

]

μ

μ



(11)



−



−

λ

[μ

]

[λ

][λ

]

(12)



−



λ

[μ

]

[λ

]μ



(13)

We also list for convenience



μ

[λ

]

μ



(14)

and



−

λ

[μ

]

[λ

]

(15)

Evidently, in this formalism, flipping helicity corresponds to interchanging the brackets



...

 and [

...

We need one more important observation. Obviously, in a tree-level diagram for n-gluon

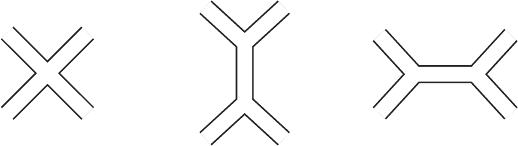
scattering, you cannot have as many 3-gluon vertices as you like. Draw the tree diagrams

for n = 4 for example (see figure N.2.3). The number of 3-gluon vertices could be either

0 or 2. In general, the number of 3-gluon vertices can be at most n − 2. You are asked to

verify this in exercise N.2.2. As remarked earlier, while the 4-gluon vertex does not involve

momentum, the 3-gluon vertex is linear in momentum. Thus, in the numerator of the

Feynman amplitude, we have n polarization vectors 

but at most n −2 momenta. We are

to form a scalar out of these Lorentz vectors by taking dot products. Clearly, there are at

least two polarization vectors who have to dance with each other. Therefore we conclude

that the tree amplitude must contain at least one power of 



. (In the n = 5 case that

power was actually 2, as we saw.)

Now we are ready to rock. For the amplitude A(++

...

+) (suppressing the momentum

labels), we simply choose the spinors μ

representing the gauge degrees of freedom to all

be equal. Then all dot products 



between polarization vectors vanish according to

(11). But we just argued that the tree amplitude must contain at least one power of 



Remarkably, we have shown that the maximal helicity-violating amplitude vanishes for any

n! Our intuition suggested that these amplitudes are suppressed, but in fact they vanish.

What about the next-to-maximal helicity-violating amplitudes with one negative helicity,

namely A(−++

...

++)? Label the gluon with negative helicity as 1. Once again, for

i =2,

...

n, choose μ

all equal to λ

. Then 



∝μ

=0, for i , j =1. Furthermore,



−



∝λ

=λ

=0 for i = 1. The amplitude A(−++

...

++) also vanishes!

Clearly, this “cheap” trick of exploiting gauge freedom no longer works for the next

amplitude with two negative helicities. To see why the trick does not work any more, look

at A(−−+

...

++) for instance. Once again we could, for i =3,

...

n, choose μ

all equal

N.2. Gluon Scattering | 491

(a)

(b)

(c)

Figure N.2.3

so that 



=0 for i, j ≥3, but then we don’t have enough freedom to make all the other

polarization dot products vanish. In fact, at some point, we better have some nonvanishing

amplitudes. In the literature, these amplitudes with two negative helicities are called

maximal helicity-violating amplitudes. Upon crossing two of the gluons, they describe

two gluons producing n − 2 gluons, with helicities ++→++

...

+, −+→−+

...

and −−→−−+

...

Explicit calculation of A(1,2,3,4)

The n = 4 case is the simplest. Take a deep breath and try to calculate A(1

−

)

and A(1

−

). For 4-gluon scattering these two are the only nonvanishing tree

amplitudes, since by parity the amplitudes with three minuses are related to the amplitudes

with three pluses (which we know vanish), and so on.

The bad news is that the calculation is fairly involved. The good news is that we can still

exploit gauge freedom mercilessly and that the final answer is surprisingly simple.

Tackle A(1

−

) first. The relevant diagrams are shown in figure N.2.3. Let us

simplify the notation as much as possible: write 12=λ

, [12] = [λ

], and so forth.

Now we need the colored Feynman rules in the form given in appendix 1. In line with

the preceding discussion let us choose ˜μ

=˜μ

and μ

= μ

= λ

. Then all but one

of the polarization dot products vanish. For instance, 

−



∝λ

[μ

] ∝λ

=0.

The only nonzero product is 

−



=λ

[μ

]/([λ

]μ

) =12[34]/([13]24),

where the second equality follows from our gauge choice. This implies that the quartic

diagram N.2.3a vanishes, since it involves the product of two polarization dot products.

We notice that there are only two more diagrams (fig. N.2.3b,c) rather than three. With

the traditional Feynman rules there is a diagram with 1 and 3 on the same cubic vertex.

Here we see another advantage of color stripping. We are looking at the coefficient of

tr(T

). The diagram we just described has T

next to T

and so does not

contribute to this particular color ordering.

Next, the diagram in figure N.2.3b vanishes. Look at the cubic vertex involving 2, 3, and

v (for the virtual gluon): (



+ 



+ 



), with 

understood

as a “placeholder” to be contracted with the 

∗

from the other cubic vertex. The first term